Abstract
Optimal integration of positive and negative outcomes during learning varies depending on an environment’s reward statistics. The present study investigated the extent to which children, adolescents, and adults (N = 142 8 – 25 year-olds, 55% female, 42% White, 31% Asian, 17% mixed race, and 8% Black; data collected in 2021) adapt their weighting of better-than-expected and worse-than-expected outcomes when learning from reinforcement. Participants made choices across two contexts: one in which weighting positive outcomes more heavily than negative outcomes led to better performance, and one in which the reverse was true. Reinforcement learning modeling revealed that across age, participants shifted their valence biases in accordance with environmental structure. Exploratory analyses revealed increases in context-dependent flexibility with age.
Across development, individuals learn to select adaptive actions through experience, increasingly making choices that are likely to bring about beneficial outcomes and avoiding those that are likely to result in negative consequences. While individuals learn from both good and bad experiences, an extensive body of work has suggested that learning from better-than-expected and worse-than-expected outcomes are not symmetric processes. In evaluating the likely consequences of their actions, individuals often consider recent, positive experiences to a greater extent than recent negative experiences (Daw, Kakade, & Dayan, 2002; Frank, Seeberger, & O’reilly, 2004; Gershman, 2015; Lefebvre, Lebreton, Meyniel, Bourgeois-Gironde, & Palminteri, 2017; Niv, Edlund, Dayan, & O’Doherty, 2012; Sharot & Garrett, 2016).
The asymmetric weighting of positive and negative experiences during learning leads to distorted beliefs about the value structure of the environment (Cazé & van der Meer, 2013). For example, a stand-up comedian who learns more from applause than silence may have inflated expectations about her likelihood of delivering a successful performance; a chef who weights negative reviews more heavily than positive ones may underestimate his ability to cook a good meal; and a new teenage driver who considers good outcomes — like getting to a friend’s house quickly — more than bad outcomes — like getting pulled over by the police — may believe that it is beneficial to break the speed limit.
Reinforcement learning models provide a computational framework through which to understand how valence biases during learning may lead to these types of distorted beliefs. Specifically, they provide a mathematical account of how asymmetric learning from positive and negative outcomes influences both individuals’ beliefs about the value of different actions, as well as the subsequent decisions they make. These models posit that individuals incrementally update their estimates of action values based on experienced prediction errors — the extent to which the outcomes of their actions deviate from their expectations — scaled by their learning rates (Sutton & Barto, 1998). Valence biases during learning can be captured through the use of separate learning rates for positive and negative prediction errors (Cazé & van der Meer, 2013; Daw et al., 2002). Higher positive versus negative learning rates yield upward changes in value estimates following positive prediction errors that are larger than corresponding downward changes following negative prediction errors, and vice versa.
Studies that have characterized how individuals learn from positive and negative prediction errors have found evidence for a positive learning rate asymmetry (Chambon et al., 2020; Lefebvre et al., 2017; Palminteri, Lefebvre, Kilford, & Blakemore, 2017) that leads to inflated expectations about the probability of experiencing good outcomes in the future — or an ‘optimism bias’ (Eil & Rao, 2011; Sharot, 2011; Sharot & Garrett, 2016; Sharot, Korn, & Dolan, 2011). Across many task contexts, weighting the positive outcomes of one’s choices more heavily than negative outcomes may lead to exaggerated beliefs about the relative value difference between better and worse choice options — a beneficial distortion that enhances decision-making (Lefebvre, Summerfield, & Bogacz, 2022). Similarly, in many real-world environments, this ‘optimism bias’ may likewise be beneficial. While healthy individuals often show positively biased belief-updating when learning about the probability of desirable and undesirable life events (Sharot & Garrett, 2016), individuals with depression do not show this asymmetry (Garrett et al., 2014; Korn, Sharot, Walter, Heekeren, & Dolan, 2014). Despite leading to less accurate beliefs, an ‘optimism bias’ may enhance, or be characteristic of, mental wellbeing (Taylor & Brown, 1988). In addition, optimism may promote motivation maintenance and persistence in the face of negative feedback (Sharot & Garrett, 2016). However, positive learning rate asymmetries may also lead to overconfidence (Johnson & Fowler, 2011) and heightened risk-taking (Niv et al., 2012). Thus, biased learning computations may yield both beneficial and adverse effects on individuals’ health and behavior throughout their lives.
Given the ubiquity and potential consequences of asymmetric learning from positive and negative experiences across the lifespan, many studies have sought to characterize its normative developmental trajectory. While there is evidence that a positive asymmetry in reinforcement learning emerges in childhood (Habicht, Bowler, Moses-Payne, & Hauser, 2021), the developmental trajectory of valenced learning rates varies across task contexts. For example, several recent studies have found that adults have higher negative learning rates relative to adolescents (Christakou et al., 2013) and children (Habicht et al., 2021), such that younger individuals’ choices reflect greater optimism about the value of risky or uncertain options (Moutsiana et al., 2013). Other recent studies, however, have found that relative to those of children (van den Bos, Cohen, Kahnt, & Crone, 2012) and adolescents (Chierchia et al., 2021), adults’ choices reflect higher positive learning rates for chosen options, and lower negative learning rates (Hauser, Iannaccone, Walitza, Brandeis, & Brem, 2015; Rodriguez Buritica, Heekeren, Li, & Eppinger, 2018). And in other experiments, positive and negative learning rates have followed non-linear age-related trajectories; in one study, adolescents demonstrated more negative learning rate asymmetries than children and adults (Rosenbaum, Grassie, & Hartley, 2022), and in another, they demonstrated more positive learning rate asymmetries (Eckstein, Master, Dahl, Wilbrecht, & Collins, 2021).
Different patterns of developmental variance in valenced learning rates across studies likely reflect developmental change in the adaptation of learning computations to the statistics of different environments. Learning rates are not an intrinsic feature of an individual; instead they characterize how an individual interacts with a particular environment (Eckstein, Master, Xia, et al., 2021; Eckstein, Wilbrecht, & Collins, 2021; Nussenbaum & Hartley, 2019). Across learning environments, the extent to which particular valence biases promote adaptive decision-making varies (Cazé & van der Meer, 2013; Chambon et al., 2020; Gershman, 2015; Lefebvre et al., 2022). Thus, developmental differences in valenced learning rates across studies may reflect age-related variance in the optimal integration of experienced outcomes into beliefs about the reward structure of the environment. As one example — though Christakou et al. (2013) and Chierchia et al. (2021) found opposing patterns of developmental change in valenced learning rates, adults outperformed adolescents in the tasks used in both studies, suggesting that adults’ learning rates were better optimized to the statistics of each task context. Indeed, across the developmental reinforcement learning literature, age-related change in learning rates do not show consistent patterns — instead, the most consistent pattern across studies is that optimal decision-making tends to improve from childhood to young adulthood (Nussenbaum & Hartley, 2019). Taken together, past research suggests that understanding developmental change in valenced learning requires understanding change in the flexible adaptation of learning rates to the demands of different contexts.
We sought to address directly the question of whether, across development, individuals adapt their learning rates in accordance with the structure of the environment. While the majority of developmental studies of reinforcement learning have examined how individuals learn within a single task context, here, we examined whether children, adolescents, and adults adjusted the extent to which they weighted recent positive and negative prediction errors across two different learning environments. Because learning rates scale prediction errors, the extent to which asymmetries in positive and negative learning rates distort value estimates depends on the variance in decision outcomes. Choices with highly variable outcomes evoke large prediction errors and therefore will be subject to greater distortion by asymmetric learning rates than choices with less variance in their reward outcomes (Mihatsch & Neuneier, 2002; Niv et al., 2012). Hereafter, we will refer to choices with greater variance in their possible reward outcomes as ‘riskier’ and choices with less variance in their reward outcomes as ‘safer’ (Weber, Shafir, & Blais, 2004). Under this conceptualization of risk, individuals who have positive learning rate asymmetries will tend to select riskier choices, whereas those with negative learning rate asymmetries will be more likely to avoid them (Niv et al., 2012; Rosenbaum et al., 2022). Here, we manipulated the reward statistics of the two environments such that in one, making riskier choices would lead to higher reward gain on average, whereas in the other, making safer choices was advantageous. In the context in which making risky choices was advantageous, individuals could earn more reward by weighting positive prediction errors more heavily than negative prediction errors, while the reverse was true in the other context. This task manipulation enabled us to characterize whether, across development, individuals flexibly adapted valence biases in learning based on the statistics of their environments. We reasoned that many of the apparent discrepancies across prior developmental findings could be explained by age-related increases in context-dependent adaptation of valenced learning rates. As such, we hypothesized that a.) individuals would adjust their learning rates across contexts, showing a more positive learning rate asymmetry in the context in which taking risks was advantageous, and b.) the extent to which individuals adjusted their learning rates across contexts would increase from childhood to adulthood.
Methods
Participants
154 participants aged 8 – 25 years completed the study online between March and August 2021. Participants were excluded from all analyses if they: a) interacted with their browser window (minimized, maximized, or clicked outside the window) more than 20 times throughout the learning task (n = 4), b) failed to respond on more than 10% of (20) choice trials (n = 0), c) pressed the same key on more than 40% of (80) choice trials (n = 1), or d) responded in less than 200 ms on more than 20% of (40) choice trials (n = 7) (See Supplemental Fig. 3 for distributions of these data quality metrics). After applying these exclusions, we analyzed data from N = 142 participants (N = 47 children, 8 – 12 years, mean age = 10.45 years, 26 females; N = 46 adolescents, 13 – 17 years, mean age = 15.37 years, 24 females; N = 49 adults, 18 – 25 years, mean age = 22.23 years, 28 females). We based our sample size off of previous studies that have employed computational models to investigate developmental change in value-based learning processes in samples of 50 – 100 participants (Chierchia et al., 2021; Cohen, Nussenbaum, Dorfman, Gershman, & Hartley, 2020; Habicht et al., 2021; Rosenbaum et al., 2022). We aimed to recruit a larger number of participants (150) than many of these prior studies due to our intention to examine interactions between learning environments and learning processes across age.
All participants reported normal or corrected-to-normal vision and no history of psychiatric or learning disorders. Based on self- or parent-report, 41.5% of participants were White, 31.0% were Asian, 16.9% were mixed race, 7.8% were Black and less than 1% were Native American. Two percent (N = 3) of participants did not provide their race. Additionally, 16.2% of the sample identified as Hispanic. Participants’ annual household incomes ranged from less than $20,000 to more than $500,000. We include a more detailed breakdown of participant demographics in the supplement. Participants were compensated with a $15 Amazon gift card for completing the study. They also received a bonus that ranged from $0 - $5 depending on their performance in the task.
As with our previous online study (Nussenbaum et al., 2020) participants were primarily recruited from ads on Facebook and Instagram (n = 40), via word-of-mouth (n = 28), and through our database for in-lab studies (n = 30), for which we solicit sign-ups at local science fairs and events and through fliers on New York University’s campus. Prior to participating in the online study, participants who had never completed an in-person study in our lab were required to complete a 5-minute zoom call with a researcher. During this zoom call, all participants (and a parent or guardian, if the participant was under 18 years) were required to be on camera and confirm the full name and date of birth they provided when they signed up for our online database. Adult participants and parents of child and adolescent participants were required to show photo identification so that we could verify their identities.
Once participants were verified, they were emailed a single-use, personalized link to a Qualtrics consent form. Participants could complete the study at any time within 7 days after receiving the link, as long as they had 1 hour available to complete the task in a single sitting. If participants (and their parents, if applicable) gave consent to participate and reported that their device met the technological requirements (laptop or desktop computer with Chrome, Safari, or Firefox), the consent form re-directed them to the reinforcement learning task.
Tasks
Participants completed two experimental tasks, each of which was hosted as its own Pavlovia project. Tasks were coded in jsPsych (de Leeuw, 2015) and are publicly available online: https://osf.io/p2ybw/
Reinforcement learning task.
Value-based learning.
To examine how individuals learn from outcomes that are better and worse than they expected, we adapted a version of the Iowa Gambling Task used in a previous developmental study (Christakou et al., 2013). In our version of the task, participants’ goal was to earn as many tokens as possible by drawing cards from four different colored decks. On every trial, participants viewed four colored decks of cards, in a random horizontal arrangement (Fig. 1). They had 10 seconds to select one of the decks using the ‘2’, ‘4’, ‘6’, and ‘8’ keys at the top of the keyboard. After selecting a deck, participants saw their selection highlighted for 500 ms, after which the top card flipped over to reveal its back, with its token value, for 500 ms. Each trial was separated by a 500 ms inter-trial interval, during which time the decks disappeared and then reappeared in random locations (see Supplement for an analysis of motor perseveration effects). On every trial, participants gained or lost the number of tokens on the card. At the end of the task, their tokens were converted into a monetary bonus. Participants were explicitly told that each deck had a mix of cards that would cause them to both win and lose tokens. They were also told that the cards in each of the decks were different, and that some decks were ‘luckier’ than others. Participants were instructed to try to select the ‘lucky’ decks to earn the most tokens. They were also told that the arrangement of the decks did not matter – only its color would relate to its distribution of cards.
Figure 1. Reinforcement learning task.
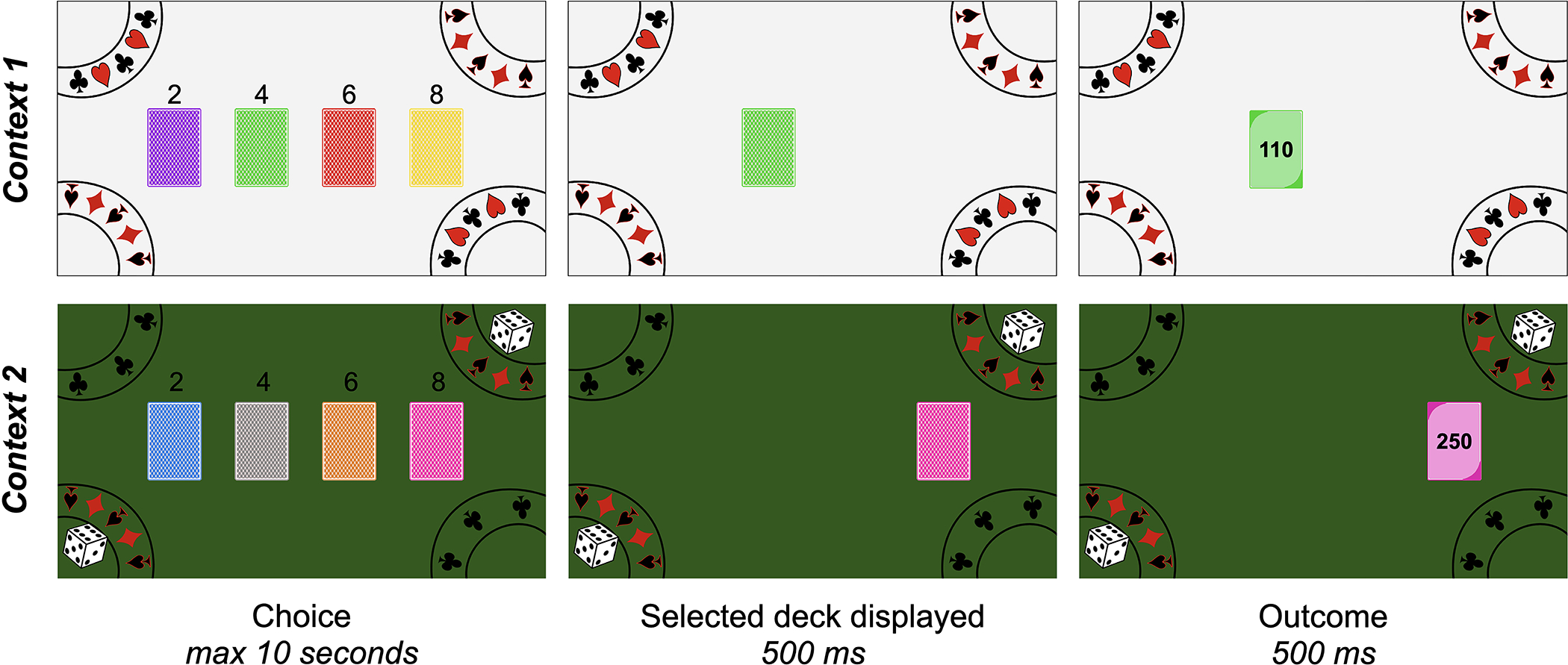
Participants completed 200 total trials of a reinforcement learning task, which was divided into two blocks. In each block, participants drew a card from one of four colored decks on every trial by pressing the ‘2’, ‘4’, ‘6’, and ‘8’ keys at the top of the keyboard. After selecting a deck, the top card flipped over to reveal its token outcome. Each deck included three cards with positive outcomes and three cards with negative outcomes. Across task contexts, the distribution of cards within each deck varied (see ‘Table 1’) such that riskier choices were advantageous in one block but disadvantageous in the other block. Participants completed the two blocks in separate ‘casino rooms’ with different colored backgrounds and different colored decks.
Participants completed two blocks of 100 choice trials; each block of choice trials was completed in a different ‘room’ of a virtual casino that had a distinct background and involved four unique decks of cards. Every 50 trials, participants were invited to take a break; they could continue by pressing a specific key when they were ready. After completing the first 100 trials, participants were told that they would complete a second round of the game in a new room of the casino. They were told that all of the card decks in this second casino room were different from those in the first room, and that they should once again try to learn which decks in this room were ‘luckier.’
The distribution of cards was different within each deck (Table 1). Every card deck had six cards with unique token values — three of these six resulted in gains, and three resulted in losses. The cards within each deck were sampled randomly with replacement, such that the probability of any specific outcome was 16.7%, and the probability of experiencing a gain or loss was always 50%, regardless of which deck was selected. In each block, two decks were ‘risky’, such that they had high gains but also high losses. Two decks were ‘safe’ and had more moderate gains and losses. Critically, in one block of the task, the average value of the risky decks was positive (25 tokens) and the average value of the safe decks was negative (−25 tokens), whereas in the other block of the task, the average value of the risky decks was negative (−25 tokens) and the average value of the safe decks was positive (25 tokens). The order of the blocks was counterbalanced across participants.
Table 1.
Card decks across block types
| Block Type | Deck Type | Positive Outcomes | Negative Outcomes | Expected Value |
|---|---|---|---|---|
|
| ||||
| Risk Good | Risky | 240, 250, 260 | −190, −200, −210 | 25 |
| Risk Good | Safe | 40, 50, 60 | −90, −100, −110 | −25 |
| Risk Bad | Risky | 180, 190, 200 | −230, −240, −250 | −25 |
| Risk Bad | Safe | 100, 110, 120 | −50, −60, −70 | 25 |
Participants were not explicitly informed about the outcome probabilities or magnitudes associated with the cards in each deck — they were only told that every deck had a mix of cards that would cause them to gain or lose tokens, and that some decks were better than others. They were also explicitly told that within a room of the casino, the mix of cards in each deck would remain constant such that decks that were ‘lucky’ early on would remain lucky throughout the entire round. In addition, though each room of the casino had two sets of two identical decks (e.g., the two ‘risky’ and two ‘safe’ decks in each room had the same distribution of cards), participants were not informed that there was any relation between any of the four colored decks.
Explicit reports.
After completing each block of 100 choice trials, participants were asked two explicit questions about the ‘luckiness’ and ‘value’ of each deck. We include a full description of this measure and our findings in the supplement.
Instructions and practice.
Prior to beginning the real trials, participants completed an extensive tutorial, which included child-friendly instructions that were both written on the screen and read aloud via audio recordings. Participants were unable to advance each instructions page until all the text had been read aloud via the audio recording. The tutorial also included 10 practice trials in a third room of the virtual casino, which was visually distinct from those used in the task, with four different colored card decks. Outcomes from the practice deck were −200, −100, 100, and 200 to show participants that cards could cause them to gain or lose points. Participants also had to respond correctly to three True/False comprehension questions before beginning the real task. If participants answered a question incorrectly, they would see the correct answer with an explanation, and repeat the question. On average, participants answered all three comprehension questions correctly in 3.16 trials (Age group means: Children = 3.19, Adolescents = 3.09, Adults = 3.20).
Reasoning task.
After the reinforcement learning task, participants were automatically directed to the Matrix reasoning item bank (MaRs-IB), which measures participants’ fluid reasoning (Chierchia et al., 2019). We previously created a version of this task to administer online (Nussenbaum et al., 2020). The task involved a series of matrix reasoning puzzles. On each trial, participants were presented with a 3×3 grid of abstract shapes, with a blank square in the lower right-hand corner. Participants had 30 seconds to select the missing shape from one of four possible answers (the target and three distractors) by clicking on it. Upon making their selection, participants saw feedback — either a green check mark for correct responses or a red X for in- correct responses — for 500 ms. Participants were all administered the same sequence of 80 puzzles, which comprises a scrambled mix of easy, medium, and hard puzzles. Participants either completed 8 minutes of puzzles or all 80 puzzles, whichever occurred first. Prior to beginning the real trials, participants went through a series of short instructions. In addition, participants completed three practice trials of “easy” puzzles. Each practice trial was repeated until the participant answered it correctly.
Questionnaires.
To explore potential relations between valence biases in learning and real-world risk-taking and depressive symptomatology, we administered several questionnaires. After the reasoning task, participants were redirected to Qualtrics, where they were administered the age-appropriate version of the Domain-Specific Risk-Taking questionnaire (DOSPERT) (Blais & Weber, 2006; Weber, Blais, & Betz, 2002) and either the Beck Depression Inventory (BDI) (Beck, Ward, Mendelson, Mock, & Erbaugh, 1961) (for adults ages 18 and older) or the Children’s Depression Inventory (CDI) (Kovacs & Preiss, 1992) (for children and adolescents ages 8 – 17). We interspersed four ‘attention check’ questions throughout the questionnaires that asked participants to select a specific multiple choice response. Three of the 142 participants included in the task analyses did not complete the questionnaires. Of the 139 participants who completed the questionnaires, 13 participants did not respond correctly to all four of the attention checks; their data were excluded from questionnaire analyses, leaving data from 126 participants (n = 40 children; n = 42 adolescents, n = 44 adults). Because the child, adolescent, and adult versions of the questionnaires included different numbers of questions, we computed a proportion for each participant for each subdomain of the DOSPERT and for the BDI/CDI that reflected their proportion of the maximum score possible.
Analysis approach
All analysis code and anonymized data are publicly available online: https://osf.io/p2ybw/
Model-free analysis methods.
Behavioral analyses were run in R version 4.1.1 (R Core Team, 2018). Mixed-effects models were run using the ‘afex’ package (Singmann, Bolker, Westfall, Aust, & Ben-Shachar, 2020). Except where noted, models included the maximal random-effects structure (i.e., random intercepts, slopes, and their correlations across fixed effects for each subject) to minimize Type I error (Barr, Levy, Scheepers, & Tily, 2013). For logistic mixed-effects models, we assessed the significance of fixed effects via likelihood ratio tests. For linear mixed-effects models, we assessed the significance of fixed effects via F tests using Satterthwaite approximation to estimate the degrees of freedom. Except where noted, age was treated as a continuous variable. Continuous variables were z-scored across the entire dataset prior to their inclusion as fixed effects in mixed-effects models. We had no a priori hypotheses about how participant sex may influence learning, so we did not include sex as a covariate in the models reported in the main text. We conducted exploratory analyses to test for sex differences in decision-making and did observe any significant effects (see Supplement).
Computational modeling.
To test how individuals updated value estimates following valenced prediction errors, we fit three variants of a standard temporal difference reinforcement learning model (Sutton et al., 1998).
One learning rate model.
After choosing a card deck (c) on trial t and experiencing the reward outcome (r), participants update their estimated value (V) of the selected deck such that:
Where α is the learning rate and δt is the prediction error: δt = r − V(c)t. The values of each card deck were initialized at 0 at the beginning of each block. All reward outcomes were divided by the maximum value (260) so that they ranged between −1 and 1.
Two learning rate model.
The two learning rate model is identical to the one learning rate model except that a positive learning rate (α+) was used when δt > 0 and a negative learning rate (α−) was used when δt < 0. This model captures the hypothesis that individuals learn differently from positive and negative prediction errors.
Four learning rate model.
The four learning rate model is identical to the two learning rate model except that separate positive and negative learning rates were estimated for each block (risk good and risk bad) of the task. This model captures the hypothesis that individuals learn differently from positive and negative prediction errors and that they adjust their weighting of valenced outcomes across different learning environments.
Choice function.
In all models, value estimates were converted to choice probabilities via a softmax function with an inverse temperature parameter (β) that governs the extent to which estimated values drive choices and a stickiness parameter (ϕ) that captures the tendency to repeat the most recent choice (Katahira, 2018):
where K is an indicator variable that is 1 for the choice option selected on the previous trial, and 0 for all other choice options. We also include model comparison results for a set of models without the stickiness parameter in the supplement. Across all models, the addition of the stickiness parameter included model fit.
Alternative models.
In addition to the three models described above, we also fit nine variants of a model with a learning rate that decayed over the course of each task block. Though these models appeared to fit the data well, they were not highly recoverable, suggesting they were overparameterized for the task. We have included a full description of these models, including analyses of parameter estimates derived from them, in the supplement.
Model-fitting procedure.
For each participant, we identified the fitted parameter values that maximized the log posterior of their choices using the fmincon function in the optimization toolbox in Matlab 2020b (The Mathworks Inc., 2020). We applied the following bounds and priors to each parameter: β: bounds = [0, 30], prior = gamma(1.2, 5) (Chierchia et al., 2021; Palminteri, Khamassi, Joffily, & Coricelli, 2015); ϕ: bounds = [−10, 10], prior = normal(0, 3); all variants of α: [0, 1], prior = beta(1.1, 1.1) (Chierchia et al., 2021). Importantly, all learning rate parameters had the same prior. We randomly initialized each parameter, drawing uniformly from within their bounds. We initialized and ran fmincon ten times per participant, and took the parameter estimates that maximized the log posterior across runs.
Model validation.
To ensure our models were distinguishable from one another, we conducted recoverability analyses. We simulated data from 500 participants for each model, randomly drawing parameters from distributions covering the full range of observed parameter values that we obtained when we fit the models to our real data (β ~ U(.15, 30); ϕ ~ t50; all values of α ~ U (0, 1)) (Wilson & Collins, 2019). We then fit each simulated dataset with each of the three models and examined the proportion of participants from each generating model best fit by each of the models fit to the data (Supplemental Fig. 5). For all three datasets, the model used to generate the data was also the best-fitting model for the majority (> 65%) of the simulations.
For the four learning rate model, our primary model of interest, we also conducted parameter recoverability analyses and posterior predictive checks (see Supplement). To ensure parameters were recoverable, we examined the correlation between the ‘true’ generating parameters that we used to simulate the data, and the fitted parameter values (Supplemental Fig. 6). For all parameters, the correlation between the ‘true’ simulated parameter value and the recovered parameter value was high (>= .77).
Results
Model-free results
Relation between age and reasoning.
First, we examined whether there was a relation between age and accuracy on the MaRs reasoning task within our sample. In line with prior findings (Chierchia et al., 2019; Nussenbaum, Scheuplein, Phaneuf, Evans, & Hartley, 2020), we observed a significant relation between age and accuracy, β = .32, SE = .08, p < .001, indicating that performance on the reasoning task improved with increasing age.
Optimal choices over time.
We next examined whether participants across ages learned to select the two optimal card decks — those with positive expected values — in each block (Figure 2). In the risk good block, making an optimal choice required participants to select one of the two decks that resulted in the largest losses on 50% of trials because they also paid out even larger gains on the other 50%. In the risk bad block, making an optimal choice required participants to forego selecting either of the two decks that paid out the largest gains because they also paid out even larger losses. To examine whether participants learned to make optimal choices over the course of each task block, we ran a mixed-effects logistic regression modeling the influence of continuous age, trial number, block type (risk good vs. risk bad), and their interactions on trial-wise optimal choices. Optimal choices were coded as 1 when participants chose risky decks in the risk good block and safe decks in the risk bad block, and 0 otherwise. Given prior research suggesting that the order in which individuals encounter different environments may influence learning (Garrett & Daw, 2020; Xu et al., 2021), we also included block number (1st vs. 2nd block) as an interacting fixed effect in our model.
Figure 2. Participant learning performance across trials.
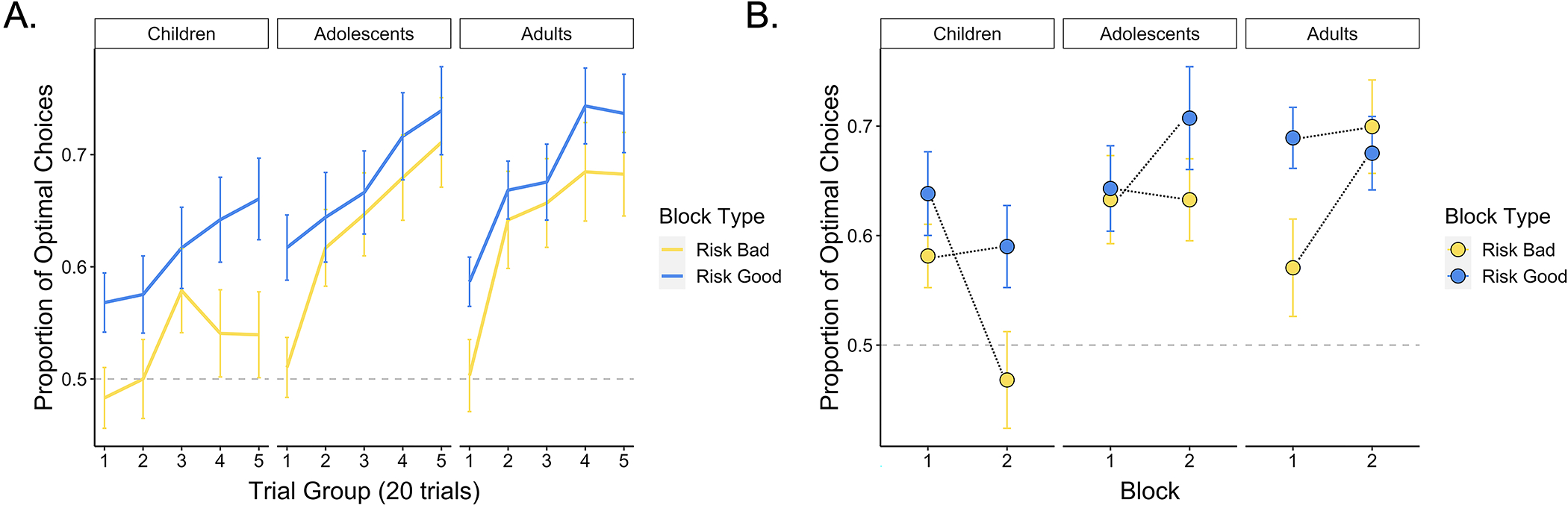
(A) Participants across age groups learned to select the two optimal card decks across trials (p < .001), though older participants demonstrated a stronger effect of trial on optimal choice performance relative to younger participants (p < .001). The lines show the average proportion of optimal choices within each trial group for each age group. Error bars show the standard error across participant means within each age group. (B) The effect of block number varied across age (p = .005), and we further observed an age × block type × block number interaction effect (p = .030). Younger participants tended to perform worse in the second block, whereas older participants performed better in the second versus first block of the task. These effects were magnified for the risk bad block — younger participants who experienced the risk bad block after the risk good block performed worse relative to those who experienced the risk bad block first, whereas older participants who experienced the risk bad block after the risk good block performed better than those who experienced it first. The points on the plot represent age-group means, and the error bars show the standard error across participant means within each age group.
We observed strong evidence for learning: Participants were increasingly more likely to choose the optimal decks as each block progressed, as indicated by a main effect of trial, X2(1) = 52.81, p < .001. In line with prior studies of value-guided choice (Nussenbaum & Hartley, 2019), we also observed a main effect of age, and an age × trial interaction, such that older participants were more likely to make optimal choices relative to younger participants, X2(1) = 6.45, p = .011, and were increasingly more likely to do so as the task progressed, X2(1) = 5.40, p = .020 (Figure 2; See Supplement for corresponding analyses of participants’ response times).
Participants’ choice behavior demonstrated signatures of an ‘optimism bias.’ If participants weighted better-than-expected outcomes more strongly than worse-than-expected outcomes, their value estimates for the risky decks should be distorted upward to a greater extent than their value estimates for the safe decks, leading them to perform better in the risk good block. Indeed, we observed a main effect of block type, X2(1) = 5.24, p = .022, such that participants performed better in the risk good relative to the risk bad block, in line with evidence for an ‘optimism bias.’ The effects of block type did not vary significantly across age, X2(1) = .52, p = .470.
We also examined model estimates of how the order in which participants encountered the risk good and risk bad contexts influenced learning. We did not observe a main effect of block number, suggesting that participants did not systematically perform better or worse in the first versus second block of the task, X2(1) = .53, p = .467. However, we did observe an age × block number interaction effect, X2(1) = 7.90, p = .005, as well as an age × block number × block type interaction, X2(1) = 4.68, p = .030, and an age × trial × block number trial interaction, X2(1) = 4.10, p = .043. In general, younger participants performed better in the first block they experienced, whereas older participants performed better in the second block. This effect was particularly strong for the risk bad block (Figure 2). This suggests that younger participants may have been biased by the first context they experienced; if they experienced the risk good context first and learned to select the riskier decks, they persisted in this strategy in the risk bad context, even when doing so was suboptimal. Older participants, however, did not demonstrate this same pattern. In general, older participants performed slightly better in the second block they encountered, suggesting that they may have learned more general task strategies in the first block that enhanced their performance in the second block.
Finally, we re-ran our model examining optimal choices including accuracy on the reasoning task as a fixed effect. All significant effects that we observed when we did not include reasoning accuracy persisted (all ps < .05), suggesting that age-related variance in task performance could not be accounted for by age-related variance in reasoning ability. In addition, reasoning ability itself did not significantly relate to task performance, X2(1) = 3.50, p = .061.
Our behavioral results suggest that children, adolescents, and adults learned through experience to make choices to bring about beneficial outcomes, both when doing so required selecting risky options that sometimes resulted in large losses, and when doing so required foregoing large gains to select safer options that resulted in more moderate gains and losses. In line with our hypothesis, learning varied across age — older participants were better at making optimal choices across contexts.
Computational modeling results
Model comparison.
After characterizing participant choice behavior, we turned to our main question of interest: To what extent were age-related differences in learning performance driven by age-related differences in valenced learning rates? To address this question, we examined whether reinforcement learning models with one, two, or four learning rates best described participants’ choices. Across age groups, model comparison revealed that participants’ choices were best captured by a model with four learning rates (Figure 3A), suggesting that participants integrated better-than-expected and worse-than-expected outcomes into their value estimates differently, and that they shifted the extent to which they weighted valenced prediction errors across task blocks (Mean Akaike Information Criteria (AIC) values: one learning rate: 466; two learning rates: 447.2; four learning rates: 437.5). Further, the four learning rate model had the lowest average AIC scores within each age group and best fit the highest proportion of children, adolescents, and adults (Figures 3B and 3C). Thus, though there was heterogeneity in the best-fitting model within each age group, model comparison suggested that across ages, the majority of participants adapted the extent to which they weighted recent positive and negative prediction errors during learning across task contexts.
Figure 3. Model comparison.
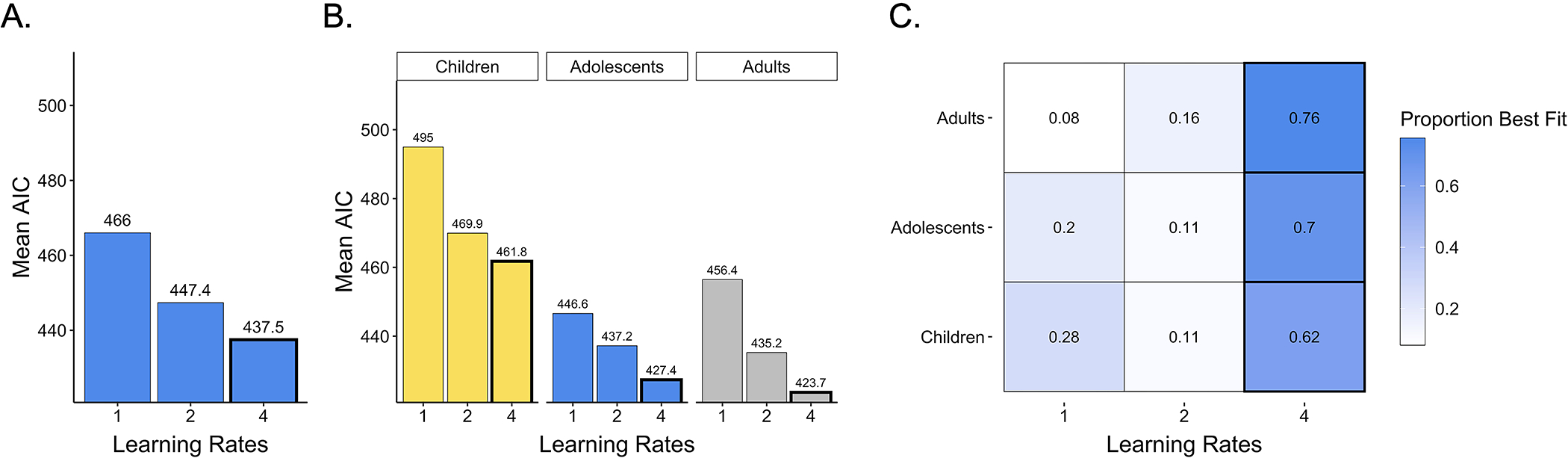
(A) Across participants, average AIC values were lowest for the four learning rate model, indicating that participants used different learning rates for both better-than-expected and worse-than-expected outcomes and across task blocks. (B) Average AIC values within each age group as well as (C) the proportion of participants best fit by each model indicated that the four-learning-rate model was also the best-fitting model within each age group.
Asymmetric learning rates and task performance.
After establishing that the four learning rate model best characterized participant choices, we examined the relation between learning rate asymmetries and task performance. For each participant, we computed a normalized ‘asymmetry index’ for each block of the task by subtracting their negative learning rate estimate from their positive learning rate estimate and dividing the difference by the sum of their positive and negative learning rates (Niv et al., 2012). These normalized asymmetry indices range from −1 to 1, with asymmetry indices of −1 indicating that participants only updated value estimates following negative prediction errors, and asymmetry indices of 1 indicating that participants only updated value estimates following positive prediction errors.
We designed our task such that higher positive versus negative learning rates would be beneficial in the risk good block and higher negative versus positive learning rates would be beneficial in the risk bad block (See Supplement). To confirm that different learning rate asymmetries were indeed optimal across different blocks of our task, we examined how participant learning rate asymmetries related to the amount of reward they earned and their proportion of optimal choices across learning contexts. In line with our manipulation, we observed AI × block type interaction effects on both the number of points participants earned in each block, F(1, 274) = 21.52, p < .001, and on the proportion of optimal choices made, F(1, 257.3) = 133.28, p < .001. These results confirmed that having a more positive AI enhanced learning and choice performance in the risk good block, and having a more negative AI enhanced learning and choice performance in the risk bad block (Fig. 4).
Figure 4. Learning rate asymmetries and task performance.
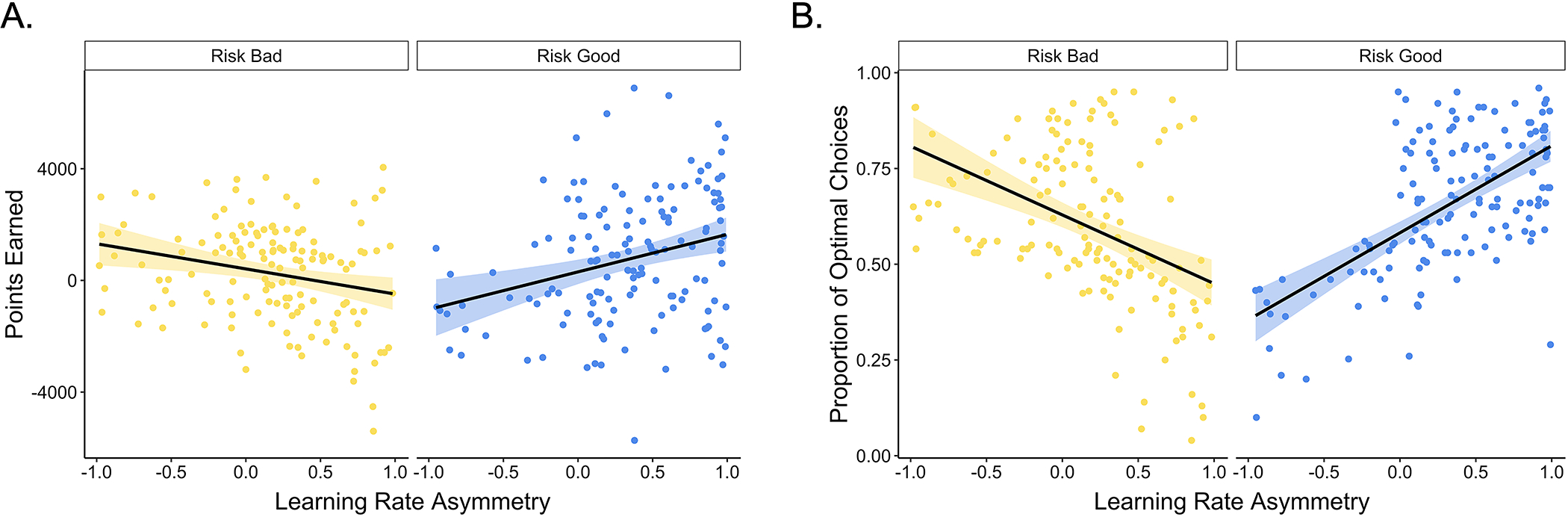
Participants with more negative learning rate asymmetries in the risk bad block (A) earned more points and (B) made more optimal choices, whereas the reverse was true in the risk good block (p < .001). The points represent individual participants’ asymmetry indices for each block. The black lines show the best-fitting linear regression lines for each block, and the shaded region around them represents the 95% confidence interval.
Adaptability of asymmetric learning rates across task contexts.
After confirming that different learning rate asymmetries were indeed beneficial across task blocks, we turned to our main question of interest: To what extent did participants flexibly adapt the extent to which they weighted positive and negative prediction errors when learning in different environments? To address this question, we ran a linear mixed effects model probing the effects of block type, block number, continuous age, and their interactions on AI. We hypothesized that participants would demonstrate flexible adaptation of their learning rates to the structure of the task, such that they would show higher AI in the risk good relative to the risk bad block, when more positive learning rate asymmetries were advantageous. In accordance with our initial hypothesis, we observed a main effect of block type, F(1, 276) = 7.28, p = .007, such that participants had more positive learning rate asymmetries in the risk good block relative to the risk bad block (Fig. 5A), when more positive learning rate asymmetries better promoted optimal choice. Thus, participants showed evidence of flexibility in valence biases during learning. Interestingly, however, participants demonstrated positive learning rate asymmetries in both blocks (Fig. 5A), in line with the ‘optimism bias’ that has been observed in prior work (Habicht et al., 2021; Lefebvre et al., 2017).
Figure 5. Learning rates across blocks.
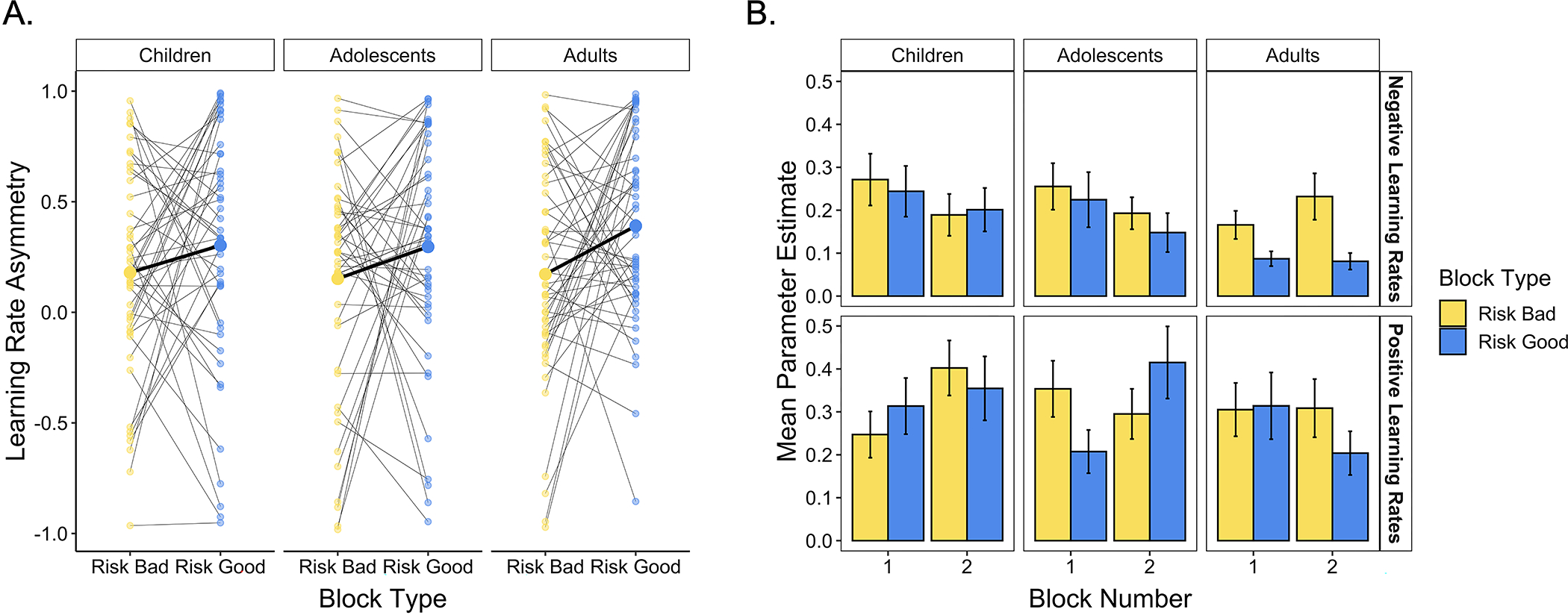
(A) Participants demonstrated more positive learning rate asymmetries in the risk good relative to the risk bad block (p = .007). The smaller dots represent individual participants’ learning rate asymmetries in each block; think black lines connect points belonging to the same participant. The larger points connected by the thicker black lines indicate means within each age group. (B) Differences in learning rate asymmetries across blocks were largely driven by differences in participants’ negative learning rates. Participants demonstrated significantly higher negative learning rates in the risk bad relative to the risk good block (p = .022). Positive learning rates did not significantly vary across block types (p = .519).
We also originally predicted that the influence of block type on AI would vary across age, with older participants showing greater flexibility in AI relative to younger participants. Contrary to this initial hypothesis, however, we did not observe a significant age × block type interaction effect on AI, F(1, 276) = 0.29, p = .589. No other main effects or interactions were significant (ps > .055). Further, we continued to observe an effect of block type on AI when we included reasoning ability as an interacting fixed effect in our model (p = .01), and we did not observe a significant block type × reasoning ability interaction effect (p > .10), suggesting that the flexible adjustment of learning rates across task contexts was not significantly related to our measure of general fluid reasoning.
Age-related differences in the flexibility of valence biases.
When we treated age as a continuous variable and analyzed learning rate asymmetries across task blocks, we did not observe a significant age × block type interaction effect on AI. However, given our a priori hypothesis that we would observe age-related increases in the adaptability of learning rates, we followed up our whole-sample analysis by examining the influence of block number and block type on AI within each age group separately. In these age group analyses, we found that only adults demonstrated a significant effect of block type on AI, F(1, 94) = 5.54, p = .021, uncorrected. In children and adolescents, the effect of block type was not significant (ps > .19), and we did not observe significant block type × block number interactions (ps > .13). In children, however, we did observe a main effect of block number, F(1, 45) = 4.38, p = .042, uncorrected, indicating that children’s learning rate asymmetries tended to be more positive in the second block they experienced. Thus, these exploratory analyses provide preliminary evidence for age-related change in the flexibility of learning rate asymmetries, with adults better adapting their learning rates to the reward structure of the environment.
Changes in learning rate asymmetries across blocks could have been driven by changes in positive learning rates, negative learning rates, or both. To better characterize age differences in learning rate adaptability, we examined the relation between continuous age, block type, block number, and positive and negative learning rates separately (Fig. 5B). We observed a main effect of block type on negative learning rates only, F(1, 138) = 5.38, p = .022; positive learning rates did not significantly vary across block types, F(1, 138) = .42, p = .519. Thus, changes in learning rate asymmetries were primarily driven by shifts in the extent to which individuals weighted recent losses when estimating the value of each card deck. We also observed effects of age on both positive and negative learning rates. For negative learning rates, we observed a main effect of age, F(1, 138) = 6.2, p = .014, such that younger participants demonstrated higher negative learning rates on average. For positive learning rates, we observed an age × block number interaction effect, F(1, 138) = 5.69, p = .018, with younger participants demonstrating higher positive learning rates in the second block they experienced, regardless of its type.
Changes in the use of value to guide decisions.
To make good choices, participants not only had to estimate the value of each card deck, they also had to effectively use those value estimates to guide decisions. Thus, while our analysis of learning rates suggest that the age-related differences we observed in choice behavior are likely at least in part due to developmental differences in the valuation process, they may also reflect developmental differences in how value estimates are translated into choice behavior. In our reinforcement learning model, the inverse temperature parameter governs the extent to which value estimates drive choice: Higher values reflect more deterministic choices that use the estimated values to a greater extent. To determine whether age-related change in the inverse temperature parameters may have influenced behavior in our task, we examined its relation with age. In line with prior studies that have found that older participants more consistently selected the option with the highest estimated value (Nussenbaum & Hartley, 2019), we found that inverse temperatures were higher in older participants, β = .17, SE = .08, p = .05. We did not observe a relation between age and choice stickiness, β = −.02, SE = .08, p = .82.
Relations with ‘real-world’ risk-taking and depressive symptoms.
Finally, we explored whether asymmetries in learning rates related to our measures of ‘real-world’ risk-taking and depressive symptomatology. We hypothesized that participants with more positive learning rate asymmetries, who were more likely to make risky choices during the task, may also be more likely to take risks in their daily life. We also hypothesized that participants with more negative learning rate asymmetries, who had more ‘pessimistic’ value estimates, may also show greater rates of depressive symptoms. To test these predictions, we computed each participant’s mean learning rate asymmetry index and ran linear regressions examining the influence of age, mean AI, and their interaction on participants’ self-reported likelihood of taking risks, their self-reported likelihood of taking financial risks, and their self-reported levels of depressive symptoms. Contrary to our hypotheses, we did not observe any relation between AI and these measures (all ps > .33).
Discussion
Prior work assessing developmental change in asymmetric learning rates has not arrived at consistent conclusions (Nussenbaum & Hartley, 2019). Here, we used a reinforcement learning task with two distinct learning contexts to test the hypothesis that the divergent patterns of learning rate asymmetries that have been observed across prior developmental studies may, in part, be due to the flexible adaptation of valenced learning rates to the demands of different environments. In line with our hypothesis, we found that individuals adjusted the extent to which they weighted positive and negative prediction errors based on the reward statistics of their environments, showing more positive learning rate asymmetries in the context in which making riskier choices yielded greater rewards and more negative learning rate asymmetries in the context in which safer choices were better. These differences in learning rate asymmetries were primarily driven by changes in negative learning rates, which were significantly higher in the context in which it was advantageous to avoid the choices that yielded the largest losses. We note, however, that when we simulated the performance of agents with many different positive and negative learning rates (see Supplement), we observed a larger influence of negative learning rates on reward earned throughout the task; thus, participants’ greater adjustment of negative versus positive learning rates may be specific to the reward statistics of this task. In exploratory analyses, we further observed preliminary evidence of age-related change in this adaptability, with adults showing a greater adjustment of learning rates across contexts relative to children and adolescents. This increased adaptability may have supported older participants’ enhanced choice performance and better differentiation of optimal and suboptimal options in their explicit reports (see Supplement), though we note that our evidence for increased adaptability in older participants is inconclusive.
In addition to observing context-dependent adaptability of learning computations, we also observed persistent biases in learning rates. In line with prior work (Chambon et al., 2020; Habicht et al., 2021; Lefebvre et al., 2017), we observed evidence for a positive learning rate asymmetry across learning environments, such that individuals more heavily weighted positive prediction errors than negative prediction errors when estimating the values of different choices. These optimistic belief-updating mechanisms inflated participants’ valuation of the riskier choice options to a greater extent than the safer choice options, leading to better performance in the environment in which making riskier choices was advantageous.
Younger participants were particularly impaired at overcoming this optimism bias. Across our measures of learning, we observed interactions between age and block number. Whereas older participants performed better in the second context they experienced, younger participants performed worse. In addition, their performance was specifically impaired in the risk bad condition when they experienced it after the risk good condition. Participants’ overall bias toward weighting positive prediction errors more heavily than negative prediction errors may have facilitated the selection of optimal choices in the risk good context, and therefore increased the difficulty of the transition from the risk good to the risk bad context. Children’s behavior in particular is consistent with the idea that adaptations to different learning environments are asymmetric (Garrett & Daw, 2020) — it is easier to transition from contexts in which making good choices requires more effort to those in which making good choices is less effortful than vice versa (Xu et al., 2021).
Our results add to the growing literature on developmental change in the adaptability of reinforcement learning computations to the statistics of the environment. Prior work has shown that adults flexibly adjust the extent to which they weight recent positive and negative prediction errors based on the underlying volatility of the environment as a whole (Behrens, Woolrich, Walton, & Rushworth, 2007; Browning, Behrens, Jocham, O’Reilly, & Bishop, 2015; Nassar et al., 2012) or of win and loss outcomes specifically (Pulcu & Browning, 2017), that they up- or down-regulate their Pavlovian bias to approach rewarding stimuli based on the utility of instrumental control (Dorfman & Gershman, 2019), and that they increase their use of more computationally costly ‘model-based’ learning strategies when doing so promotes greater reward gain (Kool, Gershman, & Cushman, 2017). While adults demonstrate effective metacontrol of the parameters that govern learning algorithms across diverse environments, our findings align with several recent studies that have found that children show reduced flexibility in the dynamic adjustment of their learning strategies. For example, relative to adults, children and adolescents demonstrate reduced stakes-based arbitration between model-free and model-based learning strategies (Bolenz & Eppinger, 2021; Smid, Kool, Hauser, & Steinbeis, 2020). A recent study (Jepma, Schaaf, Visser, & Huizenga, 2021) also found that relative to adults, adolescents demonstrated smaller differences in the proportion of risky choices that they made across contexts in which taking risks was either advantageous or disadvantageous. Our present work builds on this growing body of literature, demonstrating that, across age, the flexibility of learning computations may also influence the extent to which individuals weight the positive and negative outcomes of their choices.
Interestingly, however, our findings are in contrast to those from a previous study (Gershman, 2015), which found that adults did not adjust their valenced learning rates based on the reward statistics of different environments. Rather than manipulating the magnitudes of gains and losses as our study did, this prior study manipulated the overall reward rate of the environment. Theoretical models of optimal learning have demonstrated that in environments with low reward rates, more positive learning rate asymmetries are advantageous, whereas in environments with high reward rates, more negative learning rate asymmetries are advantageous (Cazé & van der Meer, 2013). In an empirical test of these predictions (Gershman, 2015), adult participants did not demonstrate differences in valenced learning rates across contexts with different reward rates. It is possible that adjusting learning rates based on the overall reward rate of the environment relies on different — and perhaps more demanding — computational mechanisms than adjusting learning rates based on the relative magnitudes of and variance across gain and loss outcomes in a learning environment.
Our study leaves open the question of how individuals adjust their positive and negative learning rates based on their experiences. In our task, participants had no way of knowing the optimal learning rate asymmetry ahead of time. Thus, the adjustment of learning rates across contexts must have unfolded dynamically as individuals experienced the different reward distributions across the two environments (Cazé & van der Meer, 2013). In other words, while individuals’ positive and negative learning rates determined the extent to which they weighted recent positive and negative prediction errors in updating their beliefs about the reward structure of the environment, their beliefs in turn likely shaped how they learned from experienced outcomes. At the computational level, there are multiple plausible mechanisms for how individuals may tune valenced learning rates to different environments — individuals may track the volatility and stochasticity of reward outcomes and use the variability of prediction errors or rates at which prediction errors change to scale learning rates (Behrens et al., 2007; Cazé & van der Meer, 2013; Diederen & Schultz, 2015; Gershman, 2015; McGuire, Nassar, Gold, & Kable, 2014; Nassar et al., 2012; Nassar, Wilson, Heasly, & Gold, 2010; Piray & Daw, 2021). Models that dynamically adjust learning rates based on experienced outcomes could also yield further insight into the block order effects we observed by allowing for learned information about the environment’s reward statistics to be carried over into new contexts. Biologically, the flexible adjustment of valence biases may be implemented by dopaminergic and serotonergic mechanisms (Collins & Frank, 2014; Cox et al., 2015; Daw et al., 2002; Frank, Moustafa, Haughey, Curran, & Hutchison, 2007; Michely, Eldar, Erdman, Martin, & Dolan, 2020), which undergo pronounced changes from childhood to early adulthood (Doremus-Fitzwater & Spear, 2016; Li, 2013). Thus, future studies should explicitly test different, biologically plausible algorithms through which learning rates may be dynamically updated — as well as how their underlying parameters may change across age.
Biases in valenced learning have been proposed to influence mental health (Sharot & Garrett, 2016) and risky decision-making (Niv et al., 2012), but we did not observe any relations between learning rates and participants’ reports of depressive symptomatology and real-world risk-taking. Though contrary to our hypothesis, the absence of relations between self-reported ‘real-world’ behavior and risk-taking behavior in the lab is in line with several prior studies (Radulescu, Holmes, & Niv, 2020; Rosenbaum et al., 2022). While our study was designed to examine changes in learning rate asymmetries across contexts, participants still only made choices in two highly specific learning environments. The statistics of these learning environments may not align with those that individuals encounter in their daily lives. For example, in our task, all choices were equally likely to lead to positive and negative outcomes, and these reward probabilities were perfectly stable for the duration of learning. Few choices in the ‘real world’ are equally likely to lead to good and bad outcomes, and often, individuals face changing environments where they must dissociate the stochasticity and volatility of reward outcomes (Nassar et al., 2010; Piray & Daw, 2021). Thus, the general learning biases we observed may be specific to the design of our task (Eckstein, Master, Xia, et al., 2021).
In the present study, we observed both context-dependent adaptivity in valenced learning rates as well as a general bias toward weighting positive prediction errors more heavily than negative prediction errors across contexts. It may be the case, however, that the positivity ‘bias’ itself reflects adaptivity to the structure of the environment but over a longer timescale. Across development, many individuals may more frequently encounter contexts in which a positive learning rate asymmetry is advantageous, and therefore learn to approach novel learning contexts with that bias. Indeed, children’s early life experiences influence their beliefs about the overall distribution of rewards in different learning environments (Hanson et al., 2017), the reward anticipation and processing mechanisms they employ during learning (Dillon et al., 2009; Weller & Fisher, 2013), and the decision-making biases they carry into adulthood (Birn, Roeber, & Pollak, 2017). In support of this idea, several recent studies have suggested that across environments with diverse reward statistics, more heavily weighting positive versus negative outcomes during learning from one’s own actions is advantageous, particularly when decision-making itself is ‘noisy’ (Chambon et al., 2020; Lefebvre et al., 2022). Given the diversity of contexts in which a positive learning rate asymmetry is advantageous (Lefebvre et al., 2022), such contexts may be experienced more frequently than environments in which it is advantageous to weight negative feedback more heavily, leading to a persistent optimism bias. Together with our present study, these findings suggest that learning mechanisms adapt to the structure of the environment across both long timescales, leading to more stable learning biases across distinct contexts, and short timescales, enabling flexible adjustment to rapid changes in environmental demands. Future work should focus on the construction of mechanistic models that can explain how the accumulation of experience across multiple nested environments and timescales influences the weighting of positive and negative experiences during learning across the lifespan.
Supplementary Material
Acknowledgments
We gratefully acknowledge our funders: the Department of Defense (NDSEG Fellowship to K.N.), the Jacobs Foundation (Early Career Research Fellowship to C.A.H.), the National Institute of Mental Health (R01 MH126183 to C.A.H., F31 MH129105-01 to K.N.), the National Science Foundation (CAREER Award Grant No. 1654393 to C.A.H.), the NYU Vulnerable Brain Project, and New York University (Dean’s Undergraduate Research Fellowship to J.A.V., B.T.W., and H.E.H.) We thank Alexandra Cohen, Nora Harhen, and Noam Goldway for helpful comments on the manuscript.
References
- Barr DJ, Levy R, Scheepers C, & Tily HJ (2013). Random effects structure for confirmatory hypothesis testing: Keep it maximal. Journal of Memory and Language, 68. doi: 10.1016/j.jml.2012.11.001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beck AT, Ward CH, Mendelson M, Mock J, & Erbaugh J (1961). An inventory for measuring depression. Archives of General Psychiatry, 4, 561–571. doi: 10.1001/archpsyc.1961.01710120031004 [DOI] [PubMed] [Google Scholar]
- Behrens TEJ, Woolrich MW, Walton ME, & Rushworth MFS (2007). Learning the value of information in an uncertain world. Nature Neuroscience, 10, 1214–1221. doi: 10.1038/nn1954 [DOI] [PubMed] [Google Scholar]
- Birn RM, Roeber BJ, & Pollak SD (2017). Early childhood stress exposure, reward pathways, and adult decision making. Proceedings of the National Academy of Sciences of the United States of America, 114, 13549–13554. doi: 10.1073/pnas.1708791114 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blais A-R, & Weber EU (2006). A Domain-specific Risk-taking (DOSPERT) Scale for Adult Populations. Judgment and Decision Making, 1, 33–47. [Google Scholar]
- Bolenz F, & Eppinger B (2021). Valence bias in metacontrol of decision making in adolescents and young adults. Child Development, 93, e103–e116. doi: 10.1111/cdev.13693 [DOI] [PubMed] [Google Scholar]
- Browning M, Behrens TE, Jocham G, O’Reilly JX, & Bishop SJ (2015). Anxious individuals have difficulty learning the causal statistics of aversive environments. Nature Neuroscience, 18, 590–596. doi: 10.1038/nn.3961 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cazé RD, & van der Meer MAA (2013). Adaptive properties of differential learning rates for positive and negative outcomes. Biological Cybernetics, 107, 711–719. doi: 10.1007/s00422-013-0571-5 [DOI] [PubMed] [Google Scholar]
- Chambon V, Théro H, Vidal M, Vandendriessche H, Haggard P, & Palminteri S (2020). Information about action outcomes differentially affects learning from self-determined versus imposed choices. Nature Human Behaviour, 4, 1067–1079. doi: 10.1038/s41562-020-0919-5 [DOI] [PubMed] [Google Scholar]
- Chierchia G, Fuhrmann D, Knoll LJ, Pi-Sunyer BP, Sakhardande AL, & Blakemore S-J (2019). The matrix reasoning item bank (MaRs-IB): novel, open-access abstract reasoning items for adolescents and adults. Royal Society Open Science, 6, p. 190232. doi: 10.1098/rsos.190232 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chierchia G, Soukupová M, Kilford EJ, Griffin C, Leung JT, Blakemore S-J, & Palminteri S (2021). Choice-confirmation bias in reinforcement learning changes with age during adolescence. PsyArxiv. doi: 10.31234/osf.io/xvzwb [DOI] [PMC free article] [PubMed] [Google Scholar]
- Christakou A, Gershman SJ, Niv Y, Simmons A, Brammer M, & Rubia K (2013). Neural and psychological maturation of decision-making in adolescence and young adulthood. Journal of Cognitive Neuroscience, 25, 1807–1823. doi: 10.1162/jocn_a_00447 [DOI] [PubMed] [Google Scholar]
- Cohen AO, Nussenbaum K, Dorfman HM, Gershman SJ, & Hartley CA (2020). The rational use of causal inference to guide reinforcement learning strengthens with age. NPJ Science of Learning, 5. doi: 10.1038/s41539-020-00075-3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Collins AGE, & Frank MJ (2014). Opponent actor learning (OpAL): modeling interactive effects of striatal dopamine on reinforcement learning and choice incentive. Psychological Review, 121, 337–366. doi: 10.1037/a0037015 [DOI] [PubMed] [Google Scholar]
- Cox SML, Frank MJ, Larcher K, Fellows LK, Clark CA, Leyton M, & Dagher A (2015). Striatal D1 and D2 signaling differentially predict learning from positive and negative outcomes. NeuroImage, 109, 95–101. doi: 10.1016/j.neuroimage.2014.12.070 [DOI] [PubMed] [Google Scholar]
- Daw ND, Kakade S, & Dayan P (2002). Opponent interactions between serotonin and dopamine. Neural Networks: The Official Journal of the International Neural Network Society, 15, 603–616. doi: 10.1016/s0893-6080(02)00052-7 [DOI] [PubMed] [Google Scholar]
- Diederen KMJ, & Schultz W (2015). Scaling prediction errors to reward variability benefits error-driven learning in humans. Journal of Neurophysiology, 114, 1628–1640. doi: 10.1152/jn.00483.2015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dillon DG, Holmes AJ, Birk JL, Brooks N, Lyons-Ruth K, & Pizzagalli DA (2009). Childhood adversity is associated with left basal ganglia dysfunction during reward anticipation in adulthood. Biological Psychiatry, 66, 206–213. doi: 10.1016/j.biopsych.2009.02.019 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Doremus-Fitzwater TL, & Spear LP (2016). Reward-centricity and attenuated aversions: An adolescent phenotype emerging from studies in laboratory animals. Neuroscience and Biobehavioral Reviews, 70, 121–134. doi: 10.1016/j.neubiorev.2016.08.015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dorfman HM, & Gershman SJ (2019). Controllability governs the balance between Pavlovian and instrumental action selection. Nature Communications, 10, 5826. doi: 10.1101/596577 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eckstein MK, Master SL, Dahl RE, Wilbrecht L, & Collins AGE (2021). The Unique Advantage of Adolescents in Probabilistic Reversal: Reinforcement Learning and Bayesian Inference Provide Adequate and Complementary Models. BioRxiv. doi: 10.1101/2020.07.04.187971 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eckstein MK, Master SL, Xia L, Dahl RE, Wilbrecht L, & Collins AGE (2021). Learning Rates Are Not All the Same: The Interpretation of Computational Model Parameters Depends on the Context. BioRxiv. doi: 10.1101/2021.05.28.446162 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eckstein MK, Wilbrecht L, & Collins AGE (2021). What do reinforcement learning models measure? Interpreting model parameters in cognition and neuroscience. Current Opinion in Behavioral Sciences, 41, 128–137. doi: 10.1016/j.cobeha.2021.06.004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eil D, & Rao JM (2011). The Good News-Bad News Effect: Asymmetric Processing of Objective Information about Yourself. American Economic Journal: Microeconomics, 3, 114–138. doi: 10.1257/mic.3.2.114 [DOI] [Google Scholar]
- Frank MJ, Moustafa AA, Haughey HM, Curran T, & Hutchison KE (2007). Genetic triple dissociation reveals multiple roles for dopamine in reinforcement learning. Proceedings of the National Academy of Sciences of the United States of America, 104, 16311–16316. doi: 10.1073/pnas.0706111104 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frank MJ, Seeberger LC, & O’reilly RC (2004). By carrot or by stick: cognitive reinforcement learning in parkinsonism. Science, 306, 1940–1943. doi: 10.1126/science.1102941 [DOI] [PubMed] [Google Scholar]
- Garrett N, & Daw ND (2020). Biased belief updating and suboptimal choice in foraging decisions. Nature Communications, 11. doi: 10.1038/s41467-020-16964-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Garrett N, Sharot T, Faulkner P, Korn CW, Roiser JP, & Dolan RJ (2014). Losing the rose tinted glasses: neural substrates of unbiased belief updating in depression. Frontiers in Human Neuroscience, 8. doi: 10.3389/fnhum.2014.00639 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gershman SJ (2015). Do learning rates adapt to the distribution of rewards? Psychonomic Bulletin & Review, 22, 1320–1327. doi: 10.3758/s13423-014-0790-3 [DOI] [PubMed] [Google Scholar]
- Habicht J, Bowler A, Moses-Payne ME, & Hauser TU (2021). Children are full of optimism, but those rose-tinted glasses are fading – reduced learning from negative outcomes drives hyperoptimism in children. Journal of Experimental Psychology: General. doi: 10.1101/2021.06.29.450349 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hanson JL, van den Bos W, Roeber BJ, Rudolph KD, Davidson RJ, & Pollak SD (2017). Early adversity and learning: implications for typical and atypical behavioral development. Journal of Child Psychology and Psychiatry, and Allied Disciplines, 58, 770–778. doi: 10.1111/jcpp.12694 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hauser TU, Iannaccone R, Walitza S, Brandeis D, & Brem S (2015). Cognitive flexibility in adolescence: neural and behavioral mechanisms of reward prediction error processing in adaptive decision making during development. NeuroImage, 104, 347–354. doi: 10.1016/j.neuroimage.2014.09.018 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jepma M, Schaaf JV, Visser I, & Huizenga HM (2021). Impaired dissociation of advantageous and disadvantageous risky choices in adolescents: the role of experience-based learning. Research Square. doi: 10.21203/rs.3.rs-830740 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnson DDP, & Fowler JH (2011). The evolution of overconfidence. Nature, 477, 317–320. doi: 10.1038/nature10384 [DOI] [PubMed] [Google Scholar]
- Kool W, Gershman SJ, & Cushman FA (2017). Cost-Benefit Arbitration Between Multiple Reinforcement-Learning Systems. Psychological Science, 28, 1321–1333. doi: 10.1177/0956797617708288 [DOI] [PubMed] [Google Scholar]
- Korn CW, Sharot T, Walter H, Heekeren HR, & Dolan RJ (2014). Depression is related to an absence of optimistically biased belief updating about future life events. Psychological Medicine, 44, 579–592. doi: 10.1017/S0033291713001074 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kovacs M, & Preiss M (1992). CDI. Children’s Depression Inventory. New York: Multi-Health Systems. [Google Scholar]
- Lefebvre G, Lebreton M, Meyniel F, Bourgeois-Gironde S, & Palminteri S (2017). Behavioural and neural characterization of optimistic reinforcement learning. Nature Human Behaviour, 1. doi: 10.1038/s41562-017-0067 [DOI] [Google Scholar]
- Lefebvre G, Summerfield C, & Bogacz R (2022). A normative account of confirmation bias during reinforcement learning. Neural Computation, 34, 307–337. doi: 10.1162/neco_a_01455 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li S-C (2013). Neuromodulation and developmental contextual influences on neural and cognitive plasticity across the lifespan. Neuroscience and Biobehavioral Reviews, 37, 2201–2208. doi: 10.1016/j.neubiorev.2013.07.019 [DOI] [PubMed] [Google Scholar]
- McGuire JT, Nassar MR, Gold JI, & Kable JW (2014). Functionally dissociable influences on learning rate in a dynamic environment. Neuron, 84, 870–881. doi: 10.1016/j.neuron.2014.10.013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Michely J, Eldar E, Erdman A, Martin IM, & Dolan RJ (2020). SSRIs modulate asymmetric learning from reward and punishment. BioRxiv. doi: 10.1101/2020.05.21.108266 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mihatsch O, & Neuneier R (2002). Risk-Sensitive Reinforcement Learning. Machine Learning, 49, 267–290. doi: 10.1023/A:1017940631555 [DOI] [Google Scholar]
- Moutsiana C, Garrett N, Clarke RC, Lotto RB, Blakemore S-J, & Sharot T (2013). Human development of the ability to learn from bad news. Proceedings of the National Academy of Sciences of the United States of America, 110, 16396–16401. doi: 10.1073/pnas.1305631110 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nassar MR, Rumsey KM, Wilson RC, Parikh K, Heasly B, & Gold JI (2012). Rational regulation of learning dynamics by pupil-linked arousal systems. Nature Neuroscience, 15, 1040–1046. doi: 10.1038/nn.3130 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nassar MR, Wilson RC, Heasly B, & Gold JI (2010). An approximately Bayesian delta-rule model explains the dynamics of belief updating in a changing environment. The Journal of Neuroscience: The Official Journal of the Society for Neuroscience, 30, 12366–12378. doi: 10.1523/JNEUROSCI.0822-10.2010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Niv Y, Edlund JA, Dayan P, & O’Doherty JP (2012). Neural prediction errors reveal a risk-sensitive reinforcement-learning process in the human brain. The Journal of Neuroscience: The Official Journal of the Society for Neuroscience, 32, 551–562. doi: 10.1523/JNEUROSCI.5498-10.2012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nussenbaum K, & Hartley CA (2019). Reinforcement learning across development: What insights can we draw from a decade of research? Developmental Cognitive Neuroscience, 40, 100733. doi: 10.1016/j.dcn.2019.100733 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nussenbaum K, Scheuplein M, Phaneuf CV, Evans MD, & Hartley CA (2020). Moving developmental research online: comparing in-lab and web-based studies of model-based reinforcement learning. Collabra: Psychology, 6, 17213. doi: 10.1525/collabra.17213 [DOI] [Google Scholar]
- Palminteri S, Khamassi M, Joffily M, & Coricelli G (2015). Contextual modulation of value signals in reward and punishment learning. Nature Communications, 6, 8096. doi: 10.1038/ncomms9096 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Palminteri S, Lefebvre G, Kilford EJ, & Blakemore S-J (2017). Confirmation bias in human reinforcement learning: Evidence from counterfactual feedback processing. PLoS Computational Biology, 13, e1005684. doi: 10.1371/journal.pcbi.1005684 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Piray P, & Daw ND (2021). A model for learning based on the joint estimation of stochasticity and volatility. Nature Communications, 12, 6587. doi: 10.1038/s41467-021-26731-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pulcu E, & Browning M (2017). Affective bias as a rational response to the statistics of rewards and punishments.eELife, 6. doi: 10.7554/eLife.27879 [DOI] [PMC free article] [PubMed] [Google Scholar]
- R Core Team. (2018). R: A language and environment for statistical computing (Version 3.5.1). Retrieved from https://www.R-project.org
- Radulescu A, Holmes K, & Niv Y (2020). On the convergent validity of risk sensitivity measures. PsyArxiv. doi: 10.31234/osf.io/qdhx4 [DOI] [Google Scholar]
- Rodriguez Buritica JM, Heekeren HR, Li S-C, & Eppinger B (2018). Developmental differences in the neural dynamics of observational learning. Neuropsychologia, 119, 12–23. doi: 10.1016/j.neuropsychologia.2018.07.022 [DOI] [PubMed] [Google Scholar]
- Rosenbaum G, Grassie H, & Hartley CA (2022). Valence biases in reinforcement learning shift across adolescence and modulate subsequent memory. eLife, 11, e64620. doi: 10.7554/eLife.64620 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sharot T (2011). The optimism bias. Current Biology: CB, 21, R941–5. doi: 10.1016/j.cub.2011.10.030 [DOI] [PubMed] [Google Scholar]
- Sharot T, & Garrett N (2016). Forming Beliefs: Why Valence Matters. Trends in Cognitive Sciences, 20, 25–33. doi: 10.1016/j.tics.2015.11.002 [DOI] [PubMed] [Google Scholar]
- Sharot T, Korn CW, & Dolan RJ (2011). How unrealistic optimism is maintained in the face of reality. Nature Neuroscience, 14, 1475–1479. doi: 10.1038/nn.2949 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Singmann H, Bolker B, Westfall J, Aust F, & Ben-Shachar MS (2020). Afex: analysis of factorial experiments (Version .27–2). Retrieved from https://CRAN.R-project.org/package=afex
- Smid CR, Kool W, Hauser TU, & Steinbeis N (2020). Computational and behavioral markers of model-based decision making in childhood. PsyArxiv. doi: 10.31234/osf.io/ervsb [DOI] [PubMed] [Google Scholar]
- Sutton RS & Barto AG (1998). Reinforcement Learning: An Introduction. IEEE Transactions on Neural Networks, 9, 1054. doi: 10.1109/TNN.1998.712192 [DOI] [Google Scholar]
- Taylor SE, & Brown JD (1988). Illusion and well-being: a social psychological perspective on mental health. Psychological Bulletin, 103, 193–210. doi: 10.1037/0033-2909.103.2.193 [DOI] [PubMed] [Google Scholar]
- The Mathworks Inc. (2020). MATLAB version 9.9.0.1467703 (R2020b). Natick, MA. [Google Scholar]
- van den Bos W, Cohen MX, Kahnt T, & Crone EA (2012). Striatum-medial prefrontal cortex connectivity predicts developmental changes in reinforcement learning. Cerebral Cortex, 22, 1247–1255. doi: 10.1093/cercor/bhr198 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weber EU, Blais A-R, & Betz NE (2002). A domain-specific risk-attitude scale: measuring risk perceptions and risk behaviors. Journal of Behavioral Decision Making, 15, 263–290. doi: 10.1002/bdm.414 [DOI] [Google Scholar]
- Weber EU, Shafir S, & Blais A-R (2004). Predicting risk sensitivity in humans and lower animals: risk as variance or coefficient of variation. Psychological Review, 111, 430–445. doi: 10.1037/0033-295X.111.2.430 [DOI] [PubMed] [Google Scholar]
- Weller JA, & Fisher PA (2013). Decision-making deficits among maltreated children. Child Maltreatment, 18, 184–194. doi: 10.1177/1077559512467846 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilson RC, & Collins A (2019). Ten simple rules for the computational modeling of behavioral data. Elife, 8:e49547. doi: 10.7554/eLife.49547 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu J, Van Dam NT, Luo Y, Aleman A, Ai H, & Xu P (2021). Asymmetrical adaptations to increases and decreases in environmental volatility. bioRxiv. doi: 10.1101/2021.07.30.454486 [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


