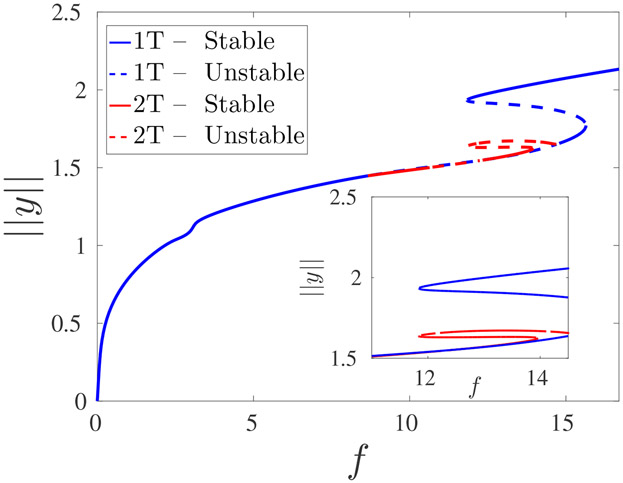
Figure 1:

A partial bifurcation diagram of a single Duffing-Helmholtz oscillator. The y-axis represents the L2 norm (the average was taken over one period of the oscillatory solution) of the solution, ∥y∥, and the x-axis represents the amplitude of the driving force, f. The inset shows the bistability region. The solid lines correspond to stable solutions while the dashed lines correspond to unstable solutions. The blue (red) lines correspond to solutions with the same (double) period of the driving force (denoted as 1T and 2T, respectively). The bifurcation diagram was numerically derived using the AUTO numerical continuation program [24].