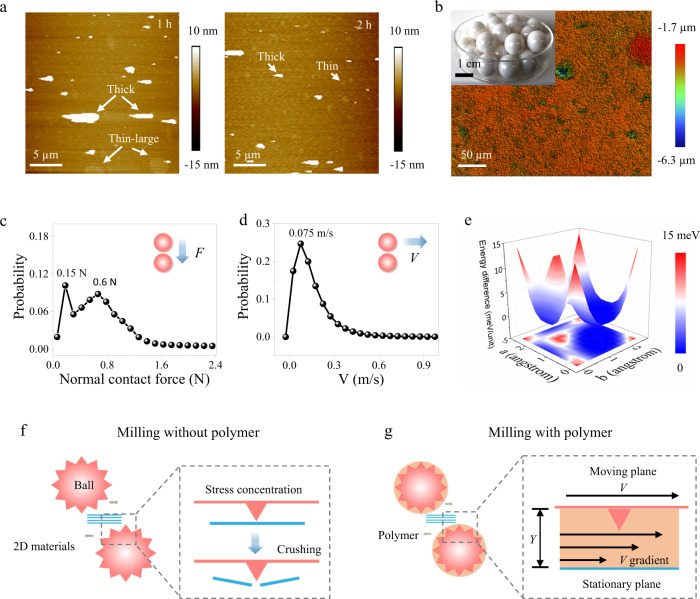
Fig. 3. Exfoliation mechanism of the sticky exfoliation.

a AFM characterization on graphene products obtained after 1 and 2 h milling, respectively. b Surface roughness of the grinding balls (d = 1 mm) characterized by an optical profilometer. Inset is a photograph of ZrO₂ grinding balls (d = 10 mm). c The statistical analysis of the normal compression force, and d the relative velocity of motions between grinding balls during ball milling process obtained by discrete element method (DEM) simulation study. e Density-functional theory (DFT) three-dimensional potential energy surface for the sliding motion of bilayer graphene. This figure was obtained by statically analyzing DFT energy difference relative to the ground state when sliding a bilayer graphene. x and y indicate the moving displacement along lattice vector direction in graphene unit. z-axis represents energy difference. The greater energy difference gradient means the harder sliding. The sliding direction with the lowest energy difference gradient is considered as the preferential direction and the energy difference gradient along the preferential direction is taken as the minimum required shearing strength for delamination. f, g Two-plane model for describing the exfoliation process when milling with and without polymer. In this model, a moving plane (grinding balls) is topped on a fixed plane (layered materials, area = A), but separated by a polymer buffer layer (thickness = Y). To initiate the dislocation, shear force applied by the polymer (F) needs to exceed the required sliding force (P × A) between two graphene layers, as represent in equation (1):$F=\rho \frac{△V}{Y}A>P\times A$ (1). where P is sliding stress (maximal 0.116 GPa by DFT calculation, Fig. 3e, Supplementary Table 5.2), and $\rho$ is the dynamic viscosity of the polymer, △V is the flow rate difference in the buffer layer, $\frac{△V}{Y}$ is the velocity (V) gradient.