Unsupervised Cross-Domain Functional MRI Adaptation for Automated Major Depressive Disorder Identification

Abstract

Resting-state functional magnetic resonance imaging (rs-fMRI) data have been widely used for automated diagnosis of brain disorders such as major depressive disorder (MDD) to assist in timely intervention. Multi-site fMRI data have been increasingly employed to augment sample size and improve statistical power for investigating MDD. However, previous studies usually suffer from significant inter-site heterogeneity caused for instance by differences in scanners and/or scanning protocols. To address this issue, we develop a novel discrepancy-based unsupervised cross-domain fMRI adaptation framework (called UFA-Net) for automated MDD identification. The proposed UFA-Net is designed to model spatio-temporal fMRI patterns of labeled source and unlabeled target samples via an attention-guided graph convolution module, and also leverage a maximum mean discrepancy constrained module for unsupervised cross-site feature alignment between two domains. To the best of our knowledge, this is one of the first attempts to explore unsupervised rs-fMRI adaptation for cross-site MDD identification. Extensive evaluation on 681 subjects from two imaging sites shows that the proposed method outperforms several state-of-the-art methods. Our method helps localize disease-associated functional connectivity abnormalities and is therefore well interpretable and can facilitate fMRI-based analysis of MDD in clinical practice.

1. Introduction

Major depressive disorder (MDD) is a mental disorder caused by a combination of genes, environment, and psychology, leading to a variety of emotional and physical problems for the patients (Lewinsohn et al., 1998; Fan et al., 2020). The long-term treatment (e.g., medication and/or psychotherapy) for this disease brings much economic burden to the society. Therefore, accurate detection of MDD is much essential in helping clinicians plan timely and early intervention. Resting-state functional magnetic resonance imaging (rs-fMRI) provides a non-invasive technique that measures spontaneous brain activity through the blood-oxygen-level-dependent (BOLD) signals. It has been widely used to investigate the functional architecture of the brain and demonstrated great clinical and practical values in computer-aided MDD diagnosis (Dutta et al., 2014; Dichter et al., 2015; Luo et al., 2021).

The research studies based on rs-fMRI for MDD identification can be mainly categorized into traditional machine learning methods and deep learning based methods. Methods belonging to the first category usually feed handcrafted fMRI features (e.g., node degree and clustering coefficient) to predefined learning models for classification. The commonly used models include support vector machines (SVMs) (Ramasubbu et al., 2016; Wang et al., 2017; Rosa et al., 2015; Sen et al., 2021), partial least squares regression (Yoshida et al., 2017), maximum margin clustering (Zeng et al., 2014), and linear discriminant analysis (Ma et al., 2013). These approaches differentiate MDD and healthy controls (HCs) by utilizing human-engineered features that require expert knowledge, which may not be optimal for subsequent classification models.

As the second category, deep learning methods have been developed for task-oriented feature extraction and model construction, demonstrating superiority over traditional learning based approaches (Bessadok et al., 2021). Research on MDD identification using deep models has been studied in recent years (Yao et al., 2020; Kong et al., 2021; Noman et al., 2021; Jun et al., 2020). Yao et al. (2020) propose a temporal-adaptive graph learning framework to capture spatial and dynamic temporal functional connectivity (FC) patterns for each subject. Noman et al. (2021) introduce a graph auto-encoder architecture to integrate anatomical structure and node information of functional connectivity networks, which are then embedded into a latent representation and fed into a fully-connected network. Kong et al. (2021) propose a spatial graph neural network with temporal fusion to capture functional connectivity-based features between adjacent sliding windows. Jun et al. (2020) incorporate effective connectivity derived from rs-fMRI with non-imaging phenotypic characteristics, and feed the combined features into a spectral graph convolutional network (GCN) for MDD classification. These studies generally use rs-fMRI data acquired from the same site with a limited sample size, thus limiting the generalizability of the constructed models.

To increase sample size and enhance statistical power, several studies (Gallo et al., 2021; Shi et al., 2021b; Liu et al., 2018) propose to leverage multi-site neuroimaging data for disease diagnosis. For instance, Gallo et al. (2021) investigate MDD identification using two consortiums (PsyMRI and REST-meta-MDD), which consist of 23 cohorts (1,039 subjects) and 25 cohorts (2,338 subjects), respectively. Shi et al. (2021b) perform MDD analysis on 2,121 subjects from 24 study centers. Even with good capability, these studies usually assume that neuroimaging data are sampled from the same distribution, and combine data from different sites/centers into a single dataset for MDD identification. That is, previous studies usually suffer from significant inter-domain heterogeneity caused for instance by the use of different scanners and/or scanning protocols, where domains represent multiple sites with different data distributions (Kouw and Loog, 2019; Guan and Liu, 2021).

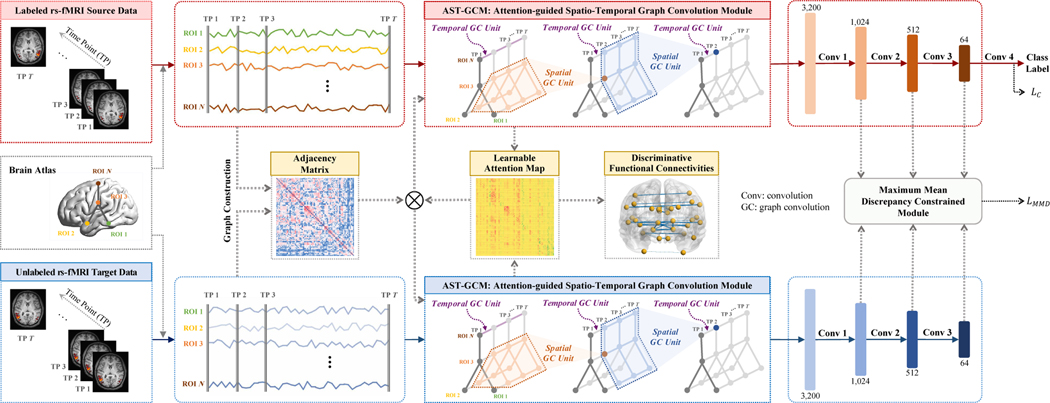
To this end, we propose an unsupervised cross-domain fMRI adaptation method (called UFA-Net) for automated MDD identification, as illustrated in Fig. 1. Our method can significantly mitigate the impact of data distribution shift across different sites, helping build models with strong generalizability. The unsupervised nature of our method facilitates the practical application of transferable models among multiple sites, without depending on category label annotations of the to-be-analyzed target domain. Specifically, we introduce a maximum mean discrepancy module to align feature maps between the labeled source and unlabeled target domains. To capture imaging features of both domains, an attention-guided spatio-temporal graph convolution module is used to characterize spatio-temporal patterns of rs-fMRI data. Experiments on 681 subjects from two imaging sites with rs-fMRI data demonstrate the superior performance of UFA-Net, compared with several state-of-the-arts. We also investigate discriminative brain functional connectivities identified by UFA-net for MDD diagnosis, and our findings are consistent with previous studies.

Fig. 1.

Illustration of the proposed unsupervised cross-domain fMRI adaptation framework (called UFA-Net) for automated major depressive disorder (MDD) identification based on resting-state functional MRI (rs-fMRI). The UFA-Net consists of four components: (1) graph construction based on standardized source and target time series for obtaining an adjacency matrix, (2) feature learning via an attention-guided spatio-temporal graph convolution module (AST-GCM), (3) feature alignment via a maximum mean discrepancy constrained module, and (4) classification. A learnable attention map is incorporated into AST-GCM to quantify discriminative capability of different functional connectivities. A hybrid loss function is used for model training, with L_C for category label prediction and L_MMD for reducing feature distribution differences between source and target data.

The contributions of this paper are summarized as follows:

• We introduce a novel discrepancy-based unsupervised cross-domain fMRI adaptation (UFA-Net) framework for automated MDD identification. To the best of our knowledge, this is one of the first attempts to investigate cross-site fMRI adaptation for MDD analysis.

• An effective maximum mean discrepancy constrained module is introduced for fMRI feature alignment between the labeled source and unlabeled target domains, and these features are automatically learned by an attention-guided spatio-temporal graph convolution module.

• Our method helps localize disease-related brain regions and functional connectivity abnormalities based on fMRI time series. This would facilitate fMRI-based MDD analysis in clinical practice.

• Comprehensive experiments on two imaging sites demonstrate that our method outperforms several state-of-the-art methods in cross-domain fMRI-based MDD identification.

The remainder of this paper is organized as follows. Section 2 briefly surveys recent studies on MDD identification and domain adaptation techniques based on fMRI data. Section 3 introduces details of the proposed method. Section 4 presents materials and experimental results. Section 5 discusses the influence of several key components of the proposed method. The paper is finally concluded in Section 6.

2. Related Work

2.1. Automated MDD Identification

The existing studies on MDD identification can be roughly categorized into two categories: (1) traditional machine learning methods and (2) deep learning methods. Traditional machine learning methods usually feed handcrafted rs-fMRI features (e.g., node degree and clustering coefficient) to predefined learning models for classification (Kim et al., 2022). The commonly used models include SVM (Drysdale et al., 2017; Ramasubbu et al., 2016; Zhong et al., 2017; Wang et al., 2017; Sundermann et al., 2017; Bhaumik et al., 2017; Rosa et al., 2015; Sen et al., 2021), partial least squares regression (Yoshida et al., 2017), maximum margin clustering (Zeng et al., 2014), and linear discriminant analysis (Ma et al., 2013) based on rs-fMRI time series data. Besides, many other imaging modalities based on traditional methods are also explored for MDD identification, such as diffusion tensor imaging (Sacchet et al., 2015b), structural MRI (Sankar et al., 2016; Sacchet et al., 2015a; Foland-Ross et al., 2015), task-based fMRI (Yang et al., 2016; Sato et al., 2015), and electroencephalogram (EEG) (Mahato and Paul, 2019).

Many deep learning methods have been proposed for rs-fMRI based brain disease diagnosis (Kong et al., 2021; Noman et al., 2021; Jun et al., 2020; Li et al., 2021). For instance, Kong et al. (2021) propose a spatial graph neural network with temporal fusion to capture functional connectivity-based features between adjacent sliding windows. Noman et al. (2021) introduce a novel graph auto-encoder architecture to integrate anatomical structure and node information of functional connectivity networks, and the derived features are embedded into a latent representation, followed by a fully-connected network to derive the final prediction. Jun et al. (2020) incorporate effective connectivity derived from rs-fMRI with non-imaging phenotypic characteristics, and the combined feature representation is fed into a spectral GCN for MDD classification.

Multi-site neuroimaging data have been increasingly used to increase sample size and enhance statistical power for automated diagnosis of brain disorders, such as the REST-meta-MDD Consortium Data Sharing dataset (Yan et al., 2019) with rs-fMRI data acquired from 17 hospitals/sites. Based on this dataset, Yao et al. (2020) propose a temporal-adaptive graph framework to capture spatial and dynamic temporal functional connectivity patterns for each subject, with experiments performed on the largest site of this dataset (i.e., Site-20 with 533 subjects). Gallo et al. (2021) use graph convolutional networks and an SVM classifier for MDD classification on 2,338 subjects. Shi et al. (2021b) perform a progressive analysis including six machine learning approaches and two dimension reduction strategies on 2,121 subjects, and find that the eXtreme Gradient Boosting (XGBoost) algorithm can achieve the optimal performance. However, these studies either simply select one site or directly integrate different sites into one cohort, ignoring significant inter-site data heterogeneity. Differently, our method considers feature distribution differences among sites and performs unsupervised fMRI data adaptation to boost the classification performance, which has not been explored yet.

2.2. Functional MRI Adaptation

In the literature, only a few studies focus on cross-site adaptation of fMRI time series. Wang et al. (2019b) present a multisite domain adaptation model, where source data are adapted to the same space as the target data via low-rank representation decomposition. Zhang et al. (2020) introduce a multisite multi-way parallel adaptation architecture, which simultaneously performs joint distribution alignment in each pair of source and target domains using optimal transport. Shi et al. (2021a) embed a three-way decision model based on triangular fuzzy similarity into unsupervised domain adaptation and optimize the pseudo-label of target data, which helps narrow the gap of data distribution among domains. Wang et al. (2020b) introduce a multi-source adaptation framework based on low-rank and graph embedding regularization, where subjects from multiple source domains can be transformed into the same target feature space, so multi-center subjects can follow consistent distribution. Zhou et al. (2019) divide the adaptation procedure into two steps, i.e., feature adaptation and classifier adaptation, which are implemented using transfer component analysis (Pan et al., 2010) and cross-domain SVM (Jiang et al., 2008), respectively. However, these studies generally utilize handcrafted fMRI features that require expert knowledge, which may not be optimal for subsequent classification models.

Several deep learning methods have been recently developed for task-oriented fMRI feature extraction and model construction. Lee et al. (2021) devise a meta-learning framework for domain generalization by calibrating domain-specific features into domain-invariant features. Wang et al. (2020a) propose an unsupervised graph domain adaptation framework, which is comprised of three modules (i.e., graph isomorphism encoding, feature alignment, and infomax regularization), to tackle cross-site/disease domain shift problems. Li et al. (2020) investigate privacy-sensitive federated learning and consider two domain adaptation methods, i.e., mixture of experts and adversarial domain alignment strategy, to address multi-site fMRI classification task. However, these studies do not capture the inherent spatio-temporal features of rs-fMRI signals. Even though Gao et al. (2019) utilize a deep cross-subject adaptation decoding method to explore spatio-temporal fMRI features, they simply transform 4D time-series data into 3D volumes and perform feature learning via a 3D convolutional neural network (3D-CNN) on these stacked volumes, ignoring the topology information of brain functional connectivity networks. Different from previous studies, in this work, we will use an attention-guided spatio-temporal graph convolution module to characterize spatio-temporal and topological features of fMRI data, and also automatically locate disease-associated brain regions.

3. Methodology

In this work, we are interested in training network using labeled source and unlabeled target data to make accurate predictions on the target domain. As shown in Fig. 1, we propose a discrepancy-based unsupervised fMRI adaptation method (called UFA-Net) that can align feature distributions between labeled source and unlabeled target domains. The UFA-Net consists of 4 parts: (1) graph construction, (2) feature learning through an attention-guided spatio-temporal graph convolution module, (3) feature alignment through a maximum mean discrepancy constrained module, and (4) a classification module.

3.1. Graph Construction

The brain is a complicated system where segregated brain regions are connected in a functional manner. The functional brain network is usually modelled as a graph due to its non-euclidean graph structure/geometry, with interactions (graph edges) between different objects (graph nodes). In brain network analysis, graph nodes are often defined as brain regions-of-interest (ROIs) and graph edges usually represent functional connections among these ROIs. Constructing such a function brain graph helps understand the functional organization of the brain, and this practice has been verified by many studies (Ktena et al., 2017; Wang et al., 2021).

In this work, the input rs-fMRI BOLD signals for each subject can be represented as an undirected spatio-temporal graph $G=(V,E)$, where each ROI at the t-th time point serves as a specific node in the vertex set $V=\left\{v_{ti}\mid t=1,\cdots ,T;i=1,\cdots ,N\right\}$. Here, T denotes the number of time points during the scanning session, and N denotes the number of brain ROIs. The graph edge set $E$ is comprised of two subsets: (1) inter-ROI connection set $E_R=\left\{\left(v_{ti},v_{tj}\right)\right\}$ between the i-th and j-th ROIs at the t-th time point, and (2) inter-time-point connection set $E_T=\left\{\left(v_{ti},v_{(t+1)i}\right)\right\}$ that connects the same i-th ROI in two consecutive time points (i.e., t and t + 1). At each time point, we construct inter-ROI functional connections $E_R$ between any pair of ROIs using Pearson’s correlation coefficient (PCC) and obtain a functional connectivity matrix $P\in R^{N\times N}$ to measure the linear correlation between ROIs. For each ROI in consecutive time points, the inter-time-point connections $E_T$ can be naturally defined according to temporal order without human assignment. Here, $E_R$ is designed to capture spatial dependency among functionally adjacent ROIs at the same time point by modeling spatial features/messages conveyed in inter-ROI connections. And $E_T$ is designed to model the temporal dynamics across consecutive time points, which serves as a complementary perspective to $E_R$. These two types of edges facilitate us to capture sophisticated spatio-temporal features of rs-fMRI data, allowing information to be aggregated along both spatial and temporal dimensions.

In this work, we compute the functional connectivity matrix P based on the concatenation of all source and target time series to ensure that all subjects share the same functional topology for facilitating subsequent feature learning, without using any label information of the studied subjects. After graph construction, the standardized/normalized ROI-based BOLD signals for each subject with a dimension of (1,T, N) are fed into the proposed attention-guided spatio-temporal graph convolution module for feature learning, which is detailed in Section 3.2.

3.2. Feature Learning

To learn discriminative fMRI features, we resort to an attention-guided spatio-temporal graph convolution module (AST-GCM), as illustrated in Fig. 1. AST-GCM is consisted of three components: (1) spatial graph convolutional unit for spatial feature extraction, (2) temporal graph convolutional unit for temporal feature extraction, and (3) an attention mechanism embedded into graph convolution for highlighting disease-associated functional connectivities.

3.2.1. Spatial Graph Convolutional Unit

Spatial information in rs-fMRI data indicates brain functional connectome. Effective extraction of such kind of feature helps better understand the node activity and coactivation pattern between connectivity-based ROIs. To achieve that, we introduce a spatial graph convolution (GC) unit (Gadgil et al., 2020), which aims to aggregate spatial features/messages from connectomic neighbourhoods for each brain region.

Specifically, each ROI is represented as a T-dimensional BOLD signal vector, and thus the inputs of spatial GC unit can be denoted as $f_{\mathit{\text{in}}}^0\in R^{1\times T\times N}$. For the convolutional operation at each spatial GC unit, we consider 1-hop neighbourhood of each ROI, so the size of spatial kernel W_S is 1, which is consistent with Yan et al. (2018). Following Kipf and Welling (2016), given an adjacency matrix $A\in R^{N\times N}$ (A = P in this work) characterizing inter-ROI connections at each time point and an identity matrix I indicating self-connections, the output $f_{s_{-}out}^l\in R^{c_{s\text{\_}out}\times T\times N}$ generated by the l-th spatial GC unit can be represented as:

$$f_{s_{-}out}^l={\text{Λ}}^{-\frac{1}{2}}(A+I){\text{Λ}}^{-\frac{1}{2}}{f}_{in}^{l-1}{W}_S^l,$$ (1)

where Λ is a diagonal matrix with its i-th diagonal element as ${\text{Λ}}_{ii}=\sum _j\left(A_{ij}+I_{ij}\right)$. Here, ${\text{Λ}}^{-\frac{1}{2}}(A+I){\text{Λ}}^{-\frac{1}{2}}$ is a normalized adjacency matrix to maintain the scale of the outputs. The channel size $c_{s_{-}out}$ of the output features $f_{s\_\mathit{\text{out}}}^l$ is set to 16. The practice described in Eq. (1) can be regarded as a message passing process, where spatial features among functionally adjacent ROIs are captured. The spatial feature map $f_{s\_\mathit{\text{out}}}^l$ is then fed into a temporal graph convolutional unit (detailed in Section 3.2.2) in order to learn temporal features of rs-fMRI for MDD diagnosis.

3.2.2. Temporal Graph Convolutional Unit

Functional MRI data are inherently acquired in a spatio-temporal structure, but many studies ignore the intrinsic temporal characteristics (Ktena et al., 2017; Li et al., 2019). It has been verified that the incorporation of temporal features in fMRI helps us understand the pathophysiological conditions (Zhang and Hu, 2020). In this study, we employ a temporal graph convolution (GC) unit to model the temporal dynamics across consecutive MRI volumes. Note that each ROI within one volume is connected to the same ROI in its consecutive volume(s). Specifically, we perform temporal convolution (i.e., a standard 1D convolutional operation) on the spatial feature maps $f_{s\_\mathit{\text{out}}}^l$ at the l-th layer. That is, the output features generated by the spatial GC unit serve as the inputs of the temporal GC unit. This procedure can be formulated as:

$$f_{st\_out}^l=\psi \left(\varphi \left(f_{s\_out}^l\right)\ast W_T^l\right),$$ (2)

where ∗ denotes temporal convolution, W_T denotes the 1D convolutional operation (kernel size: γ×1) performed for each ROI. γ = 11 represents the temporal range of the neighbourhood across consecutive time points, which is consistent with Gadgil et al. (2020). Here, ϕ indicates the BN-ReLU operation, where BN denotes batch normalization (Ioffe and Szegedy, 2015) for feature standardization and ReLU denotes the rectified linear unit (Agarap, 2018) to avoid vanishing gradient. Also, ψ represents the BN-Dropout operation that randomly dropouts output features with a probability of 0.5 to avoid overfitting.

The temporal GC unit investigates brain function from a complementary perspective to spatial information. Through the spatial and temporal GC (ST-GC) units, we can explicitly model both spatial and temporal patterns of fMRI and obtain the output feature map $f_{st\_out}^l\in R^{c_{st\_out}\times T\times N}\left(c_{st\_out}=16\right)$. For efficient feature extraction and abstraction, four hierarchical ST-GC units are included in the proposed AST-GCM (with three units shown in Fig. 1 for simplicity). Note that for l > 1, $f_{in}^{l-1}$ in Eq. (1) is equal to $f_{s{t}_{-}out}^{l-1}$. Through multiple stacked ST-GC units, the hierarchical spatial features between multi-hop ROIs based on functional topology and rich temporal features across consecutive time points can be well characterized.

3.2.3. Attention Mechanism

To characterize unique contributions of different functional connectivities to disease diagnosis, we further embed a learnable attention matrix/mask $M\in R^{N\times N}$ into the adjacency matrix A to quantify the importance of each functional connectivity between a pair of ROIs. In this attention mask, off-diagonal elements with larger values denote functional connectivities that are more discriminative for MDD diagnosis.

Specifically, we replace A + I in Eq. (1) with $(A+I)\otimes M$, where ⊗ denotes the element-wise multiplication between two matrices and M is the to-be-learned attention mask. When conducting spatio-temporal graph convolution on a brain ROI, the elements in A are expected to model the contribution of functional connectivities between this ROI and its neighbourhoods. Note that this attention mask can be learned automatically via the proposed model in a data-driven manner. This makes our model well interpretable in detecting MDD-associated functional connectivity abnormalities, thereby facilitating fMRI-based analysis of MDD in clinical practice.

3.3. Feature Alignment

To explicitly reduce the feature distribution gap between source and target data, we employ a maximum mean discrepancy constrained module to minimize the feature difference between two domains at three convolutional layers (see Fig. 1). Note that we do not perform feature alignment on low-level features such as intermediate features generated from two AST-GCM components. The reason is that these features may contain very limited semantic information, and thus, adapting these low-level features could be less effective for category-level classification. We will further study the influence of feature alignment at different layers in Section 5.3.

The proposed feature adaptation module aims to minimize a maximum mean discrepancy constrained loss function L_MMD, which is defined as:

$$L_{MMD}=\frac{1}{N_s^2}\sum _{j=l_1,l_2,l_3}{\left|f_{src}(j)-f_{tgt}(j)\right|}^2,$$ (3)

where f_src and f_tgt are feature maps obtained from the labeled source and unlabeled target domain, respectively, N_s indicates the number of subjects in one training batch, while l₁, l₂, and l₃ denote the last three convolutional layers with 1,024, 512, and 64 channels, respectively. With Eq. (3), we can explicitly align feature distributions of two domains, thus alleviating inter-site data heterogeneity. Since the maximum mean discrepancy constrained loss function can be jointly optimized with the whole network, such a feature alignment module is also expected to constrain the feature extraction module (i.e., AST-GCM) to generate fMRI features shared by both domains.

3.4. Classification

Based on labeled source data, a classification module is designed for disease diagnosis, including a convolutional operation (kernel size: 1×1) and a sigmoid activation function. Thus, a hybrid loss function L is used for training the proposed UFA-Net, consisting of two components: (1) a binary cross-entropy loss function L_C for predicting category labels of source data, and (2) a maximum mean discrepancy constrained loss L_MMD for inter-domain feature alignment. Here, L_C aims to minimize the difference between the predicted classification probability and the ground-truth label for the labeled source domain, and it can be represented as:

$$L_C=-\sum _i{y}_{i}log\left(p_i\right)+\left(1-y_i\right)log\left(1-p_i\right),$$ (4)

where $p_i\in [0,1]$ indicates the probability of the i-th source subject belonging to the patient category, and $y_i\in \{1,0\}$ denotes the ground-truth category label (i.e., 1 for MDD, and 0 for HC).

The hybrid loss function of the proposed UFA-Net is then formulated as follows:

$$L=L_C+\lambda L_{MMD},$$ (5)

where λ is a hyperparameter that tunes the specific contributions of the two terms. In this work, λ is set to 1 empirically, and we will experimentally investigate the influence of λ in Section 5.1.

3.5. Implementation

In the proposed UFA-Net model, the AST-GCM component for the source domain shares the same network architecture and network parameters with those for the target domain The inputs of AST-GCM ($f_{in}^0$) are standardized/normalized ROI-based BOLD signals for each subject, with a dimension of (1,T, N). Each AST-GCM produces a feature map with a dimension of (c_{st_out}, T, N). This map is then averaged across the N dimension to accumulate features across all ROIs, and thus a feature map with a dimension of (c_{st_out}, T) is derived. This compressed feature is then fed into the maximum mean discrepancy constrained module for feature alignment and the classification module for label prediction of source data.

Our model is trained via a two-step optimization algorithm. In the first step, we train the UFA-Net based on the source domain in a supervised manner to narrow the parameter search space (with 40 epochs). In the second step, the pre-trained UFA-Net (via step 1) is further optimized based on all labeled source and unlabeled target data. During the inference process, all target samples are used as test data for prediction, making our proposed UFA-Net a transductive learning method. The proposed model is implemented using Python based on the PyTorch package (Paszke et al., 2017), and the experiment is performed on a GPU (NVIDIA TITAN Xp) with 12GB of memory. The stochastic gradient descent (SGD) optimizer is used as the optimization method, and a mini-batch of size 128 is used for model training. The initial learning rate is set to 0.01 and reduced by a factor of 2 every 30 epochs, with a total of 100 training epochs. The source code is available online¹.

4. Experiments

4.1. Materials

4.1.1. Data Acquisition

The REST-meta-MDD Consortium (Yan et al., 2019) is employed to validate the effectiveness of our proposed method. This dataset contains rs-fMRI data acquired from 25 research groups from 17 Chinese hospitals/sites, among which we select two different sites (i.e., Site-20 and Site-1) as the source and target domains, respectively. The Site-20 with 533 subjects (282 MDD patients and 251 matched HCs) is treated as the source domain, collected using a Siemens Tim Trio 3T MRI scanner with a 12-channel coil. For each scan, the slice thickness is 3.0 mm, echo time (TE) is 30 ms, repetition time (TR) is 2,000 ms, slice number is 32, flip angle is 90°, voxel size is 3.44 × 3.44 × 4.00 mm³, field-of-view (FOV) is 220 × 220, and the number of time points is 242. The Site-1 with 148 subjects (74 MDD patients and 74 matched HCs) is used as the to-be-analyzed target domain, collected using a Siemens Tim Trio 3T MRI scanner with a 32-channel coil. For each scan, the slice thickness is 4.0 mm, TE is 30 ms, TR is 2,000 ms, slice number is 30, flip angle is 90°, voxel size is 3.28 × 3.28 × 4.80 mm3, FOV is 210 × 210, and the number of time points is 210. The detailed demographic information of subjects from both source and target domains is summarized in Table 1. Note that there exist significant differences (p < 0.05) for subjects across two sites in terms of age/education via two-tailed two-sample t-test.

Table 1.

Demographic characteristics of the studied subjects from two sites (i.e., Site-20 and Site-1) in the REST-meta-MDD Consortium (Yan et al., 2019). MDD: major depressive disorder; HC: healthy control; M/F: Male/Female; Edu: education; std: standard deviation.

Group	Site-20 (Source Domain)		Site-1 (Target Domain)
	MDD	HC	MDD	HC
Subject #	282	251	74	74
Gender (M/F)	99/183	87/164	31/43	32/42
Age (mean±std)	38.74±13.74	39.64±15.87	31.72±8.19	31.80±8.99
Edu (mean±std)	10.78±3.61	12.97±3.94	13.80±2.94	15.23±2.26

4.1.2. Data Pre-Processing

A standardized pre-processing protocol based on Data Processing Assistant for Resting-State fMRI (DPARSF) (Yan and Zang, 2010) is implemented on rs-fMRI scans from both sites, including discarding the first 10 volumes, slice timing correction, head motion estimation, bandpass filtering, regression of nuisance covariates (i.e., head motion parameters, white matter, and cerebrospinal fluid), co-registration between T1-weighted images and mean functional images, and transformations from individual native space to the Montreal Neurological Institute (MNI) template space. Finally, the rs-fMRI BOLD signals for each subject are extracted, with a size of T × N, where T and N denote the number of time points and the number of ROIs, respectively. In this work, we use the Automated Anatomical Labeling (AAL) atlas with N = 116 ROIs for brain parcellation. Furthermore, we standardize each ROI’s BOLD signal across all subjects with the z-score normalization strategy (called Norm-eachROI-allSubj), and the resulting signals are used as the inputs of the proposed model. We will also study the influence of different normalization strategies in Section 5.5.

4.2. Competing Methods

We compare our proposed UFA-Net with five conventional methods, i.e., (1) BC-SVM-N, (2) BC-SVM-G, (3) BC-SVM-N-G, (4) XGBoost (Shi et al., 2021b), and (5) MaLRR (Wang et al., 2019b), and also four deep learning methods, i.e., (6) Wck-CNN (Jie et al., 2020), (7) LSTM (Graves, 2012), (8) STNet (Wang et al., 2019a), and (9) DANN (Ganin and Lempitsky, 2015).

1. BC-SVM-N: In this method, we first build a stationary functional connectivity matrix for each subject based on PCC to measure linear correlation between any pair of ROIs. Then, seven node-based brain connectivity (BC) features are extracted based on the functional connectivity matrix, including node degree, node strength, local efficiency, eigenvector centrality, modularity, clustering coefficient, and node betweenness centrality. The definition and detailed implementations of these manually-designed features can be found in Rubinov and Sporns (2010), and they are widely used in brain functional connectivity network analysis (Hong et al., 2013; Mijalkov et al., 2017; Jakab et al., 2019). These features are then concatenated to an 812-dimensional vectorized representation for each subject and fed into a linear SVM for classification.

2. BC-SVM-G: In this method, we also construct a functional connectivity matrix first, based on which five graph-based topology features (i.e., density, global efficiency, assortativity coefficient, characteristic path length, and transitivity) are extracted, forming a 5-dimensional feature vector for each subject. A linear SVM is then used to produce the final prediction.

3. BC-SVM-N-G: Since node-based and graph-based features reflect spatial and topological characteristics of rs-fMRI data, respectively, we further combine them to form an 817-dimensional feature representation for each subject, which is then fed into a linear SVM for further classification.

4. XGBoost (Shi et al., 2021b): In this method, a functional connectivity matrix based on PCC is first constructed for each subject. Then, the upper triangle elements of the matrix are flattened and converted into a 6,670-dimensional vectorized representation, which is then fed into an XGBoost model. Following Shi et al. (2021b), the parameters of XGBoost are set as follows: maximum tree depth is set to 5, minimum sum of instance weight in a child is set to 1, subsample ratio of the training instance is set to 0.8, subsample ratio of columns for each tree is set to 0.8, boosting learning rate is set to 0.1, and the coefficient of the l₁ regularization term is set to 0.01.

5. MaLRR (Wang et al., 2019b): This method develops a multi-site domain adaptation framework via low-rank representation (LRR) decomposition based on rs-fMRI signals. Specifically, we first transform the source and target domain into a common feature space via LRR, and then linearly represent each source sample using all target samples. Following Wang et al. (2019b), the transformed source and target data are finally fed into a linear SVM for classification.

6. Wck-CNN (Jie et al., 2020): This method introduces a weighted correlation kernel based CNN (Wck-CNN) to capture hierarchical rs-fMRI features for end-to-end brain disease diagnosis based on time series data. The interaction information among brain ROIs is conveyed by sequentially extracting local (i.e., region-specific), global (i.e., whole-brain-specific), and temporal features using different convolutional layers. Following Jie et al. (2020), the channel numbers of the convolutional layers are N × T₁ × M₁, 1×T₂ × M₂, and 1×1× M₃, respectively. Here, M₁, M₂, and M₃ represent the corresponding kernel numbers (with M₁ = 32, M₂ = 64, M₃ = 64), respectively, while T₁ and T₂ denote the total operations of using kernel along the temporal dimension (with T₁ = 33, T₂ = 32), respectively.

7. LSTM (Graves, 2012): This method is a popular recurrent neural network (RNN) architecture that is widely used to process sequential data by modeling the long-term time dependencies of the inputs, e.g., rs-fMRI analysis (Dvornek et al., 2017; Li and Fan, 2018). In this method, each recurrent cell has a hidden state of dimension 256, and the output of the last hidden layer is fed into a fully-connected layer to produce the final classification result. A dropout of 0.5 is utilized after each hidden layer to prevent the model from overfitting.

8. STNet (Wang et al., 2019a): This method effectively incorporates the spatial and temporal information of the rs-fMRI time series to perform disease identification. Specifically, the rs-fMRI data are first segmented into a sequence of overlapping sliding windows, followed by a series of convolutional operations to capture the spatially-dependent patterns within each window. Then, many LSTM models are employed to mine the whole-brain temporal dynamics of the complete time series. Lastly, the output of the LSTM models is fed into a fully-connected layer to perform classification.

9. DANN (Ganin and Lempitsky, 2015): This is a popular unsupervised domain adaptation method, which encourages domain invariance in feature space. In specific, a shared encoder is first leveraged to extract features from both source and target domain. Then, a domain discriminator connected to the feature extractor via a gradient reversal layer is utilized to differentiate which features come from which domain, encouraging that feature distribution of the source domain is indistinguishable from that of the target domain. Similar to our method, a binary cross-entropy loss function is used to minimize feature distribution difference between source and target domains.

Among all the competing methods, three methods (i.e., MaLRR, Wck-CNN, and STNet) are originally designed to process fMRI time series, hence being considered for comparison. The Wck-CNN characterizes the temporal properties of the brain network by performing the convolution along the temporal dimension. The LSTM directly takes the rs-fMRI BOLD signals as inputs and models long-term time dependencies of different time points. The STNet employs LSTMs to capture whole-brain temporal dynamics based on the spatially-dependent sequences, which are derived from a series of segmented windows. Two methods (i.e., MaLRR and DANN) are developed for unsupervised domain adaptation for general purposes, which aim to minimize the boundary between the source and target domains. On the other hand, these competing methods and our UFA-Net can be categorized into (1) transductive learning and (2) domain generalization learning groups. The three methods (i.e., MaLRR, DANN, and UFA-Net) are transductive learning approaches, where unlabeled target data participate in model training. The seven methods (i.e., BC-SVM-N, BC-SVM-G, BC-SVM-N-G, XGBoost, Wck-CNN, LSTM, and STNet) are implemented in a domain generalization learning manner (Zhou et al., 2022), where only source data are used for model training (without using any unlabeled target data).

We repeat the five deep learning methods 5 times independently to reduce the bias caused by parameter initialization, and record the mean and standard deviation results. Since conventional methods (i.e., BC-SVM-N, BC-SVM-G, BC-SVM-N-G, XGBoost, and MaLRR) do not require initialization, we perform only one experiment with these methods. For each competing method, we tune its adjustable hyperparameters to achieve the optimal classification results. Experimental results of two competing methods using different parameters can be found in Supplementary Materials.

4.3. Experimental Settings

For a fair comparison, all methods share the same experimental setting, with Site-20 as the source domain and Site-1 as the target domain. Five evaluation metrics are used in this work, including classification accuracy (ACC), the area under the receiver operating characteristic curve (AUC), sensitivity (SEN), specificity (SPE), and precision (PRE). Denote true positive (TP) as the number of subjects that are correctly classified as the positive category (i.e., MDD), true negative (TN) as the number of subjects that are correctly classified as the negative category (i.e., HC), false positive (FP) as the number of subjects that are wrongly classified as the positive group, and false negative (FN) as the number of subjects that are wrongly classified as the negative category. Here, $\text{ACC}=\frac{TP+TN}{TP+FP+TN+FN}$, $\text{SEN}=\frac{TP}{TP+FN}$, $\text{SPE}=\frac{TN}{TN+FP}$, and $\text{PRE}=\frac{TP}{TP+FP}$.

4.4. Bound Analysis of Cross-Domain Data Adaptation

We first experimentally analyze the lower and upper bounds of the proposed UFA-Net in the task of MDD vs. HC classification based on the studied data. To get the lower bound of cross-domain classification, we only use the source data (with 533 subjects) to train the upper branch of UFA-Net, and then directly apply the trained model (called UFA-Net-LB) to the target domain (with 148 subjects) without any data adaptation technique. The UFA-Net-LB model shares the same AST-GCM as UFA-Net that extracts spatio-temporal feature characteristics of rs-fMRI data. The only difference between UFA-Net-LB and UFA-Net lies in the incorporation of the cross-domain adaptation module. To get the upper bound (UFA-Net-UB), we train and validate UFA-Net using a two-fold cross-validation strategy based only on the target data. Specifically, we randomly partition the target data (with 148 subjects) into two subsets, with each subset having equal sample size. Then, each subset is sequentially chosen as the test set, and the remaining subset is considered as the training set. The classification score is achieved by averaging the prediction results derived from the testing subsets. To avoid the bias caused by random partition, we repeat this process five times. It is noted that we only use the upper branch (see the top panel of Fig. 1) of the proposed UFA-Net to compute the lower and upper bounds experimentally, without considering the inter-site heterogeneity. The experimental results are reported in Table 2.

Table 2.

Lower bound and upper bound analysis of the proposed UFA-Net for cross-domain data adaptation in the task of MDD vs. HC classification. LB: lower bound; UB: upper bound. Results are reported in terms of “mean±standard deviation”, with best results shown in bold.

Model	ACC (%)	AUC (%)	SEN (%)	SPE (%)	PRE (%)
UFA-Net-LB	53.51±2.39	55.22±3.59	62.43±4.05	44.59±4.91	53.02±2.18
UFA-Net-UB	55.00±1.01	56.32±2.84	52.70±8.76	57.30±8.22	55.82±2.02
UFA-Net (Ours)	59.73±1.63	62.50±2.50	69.46±6.43	50.00±9.63	58.49±2.58

From Table 2, we can observe that the lower bound (e.g., ACC=53.51% and AUC=55.22%) is only slightly better than random guesses. This implies that directly applying a model trained on the source domain to the target domain is not a good solution, possibly due to significant inter-site heterogeneity. The upper bound results are not very promising either (with ACC=55.00% and AUC=56.32%), possibly due to the limited sample size in the target domain. In contrast, our UFA-Net (trained on labeled source data and unlabeled target data) yields promising performance in most cases. For instance, the UFA-Net greatly outperforms the upper bound, with an improvement of 6.18% in terms of AUC. These results imply that UFA-Net that mitigates the inter-site distribution differences can improve classification performance, which is valuable for problems with a large number of source samples and a relatively limited number of heterogeneous target samples.

4.5. Classification Performance

The results of our UFA-Net and nine competing methods in cross-domain MDD identification are reported in Table 3. We also perform two-tailed two-sample t-test on the results of UFA-Net and each competing method, with p-values reported in the last column of this table. The term denoted by ‘*’ means that the proposed UFA-Net is statistically significantly different (with p < 0.05) from a specific competing method. From Table 3, we have the following interesting observations.

Table 3.

Results of ten methods in the task of cross-domain MDD identification (i.e., MDD vs. HC classification). Three methods (i.e., MaLRR, DANN, and UFA-Net) are transductive learning approaches, where unlabeled target data participate in model training process, while the other seven methods are implemented in a domain generalization learning manner (without using target data for model training). Best results are shown in bold.

Method	ACC (%)	AUC (%)	SEN (%)	SPE (%)	PRE (%)	p-value
BC-SVM-N*	52.03	55.35	50.00	54.05	52.11	6.1e-3
BC-SVM-G*	51.35	53.45	58.11	44.59	51.19	7.5e-41
BC-SVM-N-G*	52.03	55.49	52.70	51.35	52.00	2.7e-3
XGBoost (Shi et al., 2021b)*	50.68	54.27	51.35	50.00	50.67	2.8e-5
MaLRR (Wang et al., 2019b)*	54.73	53.86	59.46	50.00	54.32	4.9e-14
Wck-CNN (Jie et al., 2020)*	53.92±1.93	54.51±5.30	52.43±26.00	55.41±23.95	54.61±2.01	3.0e-15
LSTM (Graves, 2012)*	51.62±1.10	51.91±2.77	55.95±14.14	47.30±13.05	51.48±1.02	1.6e-39
STNet (Wang et al., 2019a)	52.03±1.35	53.10±1.40	59.46±6.40	44.59±5.34	51.73±1.11	2.1e-1
DANN (Ganin and Lempitsky, 2015)*	52.43±2.32	51.86±2.61	54.32±2.62	50.54±3.88	52.39±2.26	7.1e-4
UFA-Net (Ours)	59.73±1.63	62.50±2.50	69.46±6.43	50.00±9.63	58.49±2.58	-

^‘*’means that the proposed UFA-Net is statistically significantly different (p < 0.05) from a specific competing method based on two-tailed two-sample t-test.

On one hand, the proposed UFA-Net generally significantly outperforms five traditional learning models (i.e., BC-SVM-N, BC-SVM-G, BC-SVM-N-G, XGBoost, and MaLRR) by a large margin. For instance, UFA-Net achieves the improvement of 7.7% and 7.01% in terms of ACC and AUC values compared with the BC-SVM-N-G method. Even though the XGBoost method achieves the state-of-the-art performance (ACC: 72.8%) among studies using the REST-meta-MDD Consortium (Yan et al., 2019), their original experiment is performed only on one single site (i.e., Site-20). But when applied to another domain (i.e., Site-1), its performance drops significantly (e.g., ACC=50.68%). The possible reason is that these methods only consider handcrafted features derived from rs-fMRI signals, without taking advantage of spatio-temporal characteristics conveyed in time series data.

On the other hand, compared with three deep learning methods (i.e., Wck-CNN, LSTM, and STNet) that capture spatial features and/or temporal dynamics of rs-fMRI data, our UFA-Net yields consistently better results in terms of five metrics. This may be because UFA-Net not only characterizes spatio-temporal properties of brain functional connectivity networks, but also employs an adaptation strategy to align feature distributions between the source and target domains, but these three methods simply ignore the inter-site data heterogeneity.

Furthermore, the proposed UFA-Net yields promising results when compared with two unsupervised domain adaptation methods (i.e., MaLRR and DANN), while these three methods are all implemented in the way of transductive learning. For instance, compared with DANN, the UFA-Net improves the ACC and AUC values by 7.30% and 10.64%, respectively. These results imply that learning classification-oriented spatio-temporal features (as we do in UFA-Net) helps capture more discriminative features to distinguish MDD patients from healthy controls.

To further validate the generalizability of the UFA-Net, we directly apply the well-trained model on several unseen/held-out MDD sites from the REST-meta-MDD Consortium (Yan et al., 2019), without any model retraining or finetuning, with results reported in Supplementary Materials.

4.6. Identified Discriminative Functional Connectivities

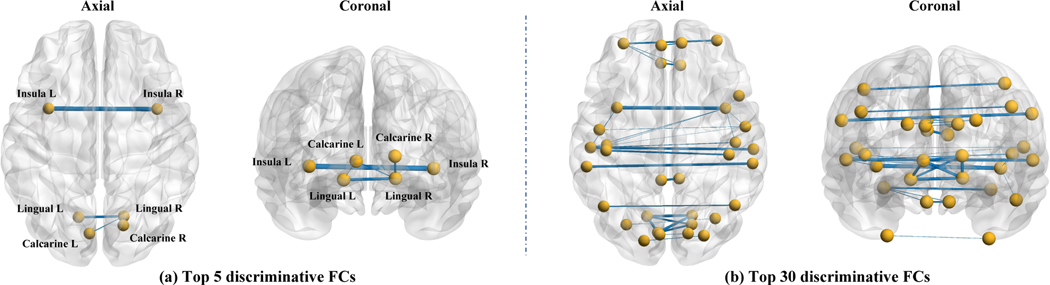
As mentioned in Section 3.2.3, an attention mechanism is utilized in the proposed UFA-Net to automatically localize disease-associated functional connectivity patterns that can differentiate patients with MDD from healthy controls. We now visualize the most discriminative functional connectivities and their associated ROIs identified by UFA-Net in Fig. 2 and Table 4, respectively. In Fig. 2, the thickest solid line denotes the most discriminative FCs, corresponding to the highest value in the attention map.

Fig. 2.

Top 5 and top 30 discriminative functional connectivities (FCs) identified by our UFA-Net in differentiating MDD subjects from healthy controls, where the thickest solid blue line denotes the most discriminative connection. L: left hemisphere; R: right hemisphere.

Table 4.

Top 5 and top 30 discriminative functional connectivities (FCs) and their associated brain regions identified by the UFA-Net. We rank these connections based on their discriminative capability for differentiating MDD from HCs in a descending manner. L: left hemisphere; R: right hemisphere.

Top-5 FCs	Top-30 FCs (column 1)	Top-30 FCs (column 2)	Top-30 FCs (column 3)
Insula_L - Insula_R Lingual_L - LinguaL_R Calcarine_R - LinguaL_R Calcarine_L - LinguaL_R Calcarine_L - Lingual_L	Insula_L - Insula_R Lingual_L - Lingual_R Calcarine_R - Lingual_R Calcarine_L - Lingual_R Calcarine_L - Lingual_L SupraMarginal_L - SupraMarginal_R Temporal Sup_L - Temporal Sup_R Cingulum Post_L - Cingulum Post_R Calcarine_L - Calcarine_R Calcarine_R - Lingual_L	Postcentral_L - Postcentral_R Frontal Mid Orb_L - Frontal Mid Orb_R Rectus_L - Rectus_R Angular_L - Angular_R Frontl Sup Medl_L - Frontl Sup Medl_R Heschl_L - Temporal Sup_L HeschLR - Temporal Sup_L Insula_L - Temporal Sup_L Frontal Mid Orb_L - Rectus_L Frontal Mid Orb_L - Rectus_R	Insula_R - Temporal Sup_L Occipital Sup_L - Occipital Sup_R Insula_R - Heschl_R Cuneus_L - Cuneus_R Rolandic Oper_L - Rolandic Oper_R Insula_R - Heschl_L Cerebelm Crus2_L - Cerebelm Crus2_R Rolandic Oper_R - Insula_R Insula_R - Templ Pole Sup_R Rolandic Oper_R - Temporal Sup_L

From Fig. 2 and Table 4, we can see that many discriminative FCs identified by UFA-Net are associated with bilateral homotopic brain regions in two hemispheres. This is consistent with previous findings that functional coordination between bilateral homotopic brain ROIs is impaired in MDD patients, while the abnormalities in homotopic connectivity across hemispheres may imply abnormal neural circuits associated with aberrant emotional processing and cognition in MDD patients (Hermesdorf et al., 2016; Yang et al., 2019; Wang et al., 2013; Guo et al., 2013). In particular, the functional connectivity between homotopic insulae has the most discriminative capability (i.e., top 1) in differentiating MDD patients from HCs, which is consistent with previous findings (Hermesdorf et al., 2016). Besides, Table 4 suggests that our identified ROIs include lingual gyrus and calcarine fissure, while their abnormal FCs have been reported in adults with major depression (Liang et al., 2020; Long et al., 2020). Also, the left superior temporal gyrus (STG), an important brain network hub in MDD patients (Su et al., 2018), appears in many discriminative FCs. A potential reason could be that gray matter volume of STG changes after depression (Inkster et al., 2009). These findings further verify the reliability of the proposed UFA-Net in identifying disease-associated functional connectivity patterns for automated MDD identification with rs-fMRI data.

4.7. Feature Interpretation from Temporal Perspective

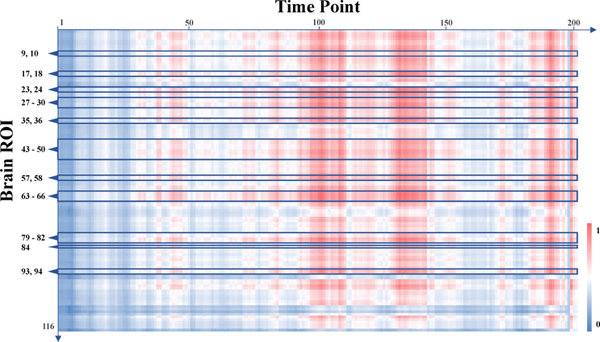
To show the characteristics derived by the proposed UFA-Net from spatial perspective, we report the identified discriminative brain ROIs in Fig. 2 and Table 4. We now try to investigate and interpret the derived fMRI features from the temporal perspective. Specifically, we first select 50 correctly-classified MDD patients and 50 correctly-classified HC subjects from the training data. We then generate the spatio-temporal feature map feature map (size: c_{st_out} × T × N) of each subject according to Eq. 2, with c_{st_out} = 16 feature channels, T = 200 time points, and N = 116 brain ROIs. The derived feature maps are then averaged across 16 channels, so each subject is represented by a map with a size of T×N. Finally, we average the feature maps of subjects within each specific group and obtain two feature maps (i.e., Map_MDD for MDD and Map_HC for HC) sized T × N. The difference between these two maps is normalized to [0, 1] and illustrated in Fig. 3, where red and blue represent large and small feature differences between MDD and HC groups, respectively. It can be seen from Fig. 3 that larger inter-group difference exists in the middle and rear parts of the entire time points. We also show the IDs of brain ROIs associated with the top 30 discriminative functional connectivities on the left side of Fig. 3. Interestingly, we find the inter-group feature difference is generally large among these ROIs, which further verifies the rationality of our identified discriminative ROIs detailed in Section 4.6.

Fig. 3.

Visualization of group-level feature differences learned by the proposed method from temporal perspective. Red and blue represent large and small feature differences between MDD patients and HC subjects, respectively. The ROIs noted on the left side are all brain regions associated with top 30 discriminative functional connectivities (refer to Table 4), and the ROI IDs are consistent with those in standard AAL-116 template.

It is worth noting that the overall performance of our UFA-Net and the nine competing methods in MDD vs. HC classification is not that promising, as shown in Table 3. And thus, the discriminative power of functional connectivity and temporal features identified by the UFA-Net may be negatively affected. It is necessary to develop more advanced techniques to further improve classification performance and generate more reliable fMRI biomarkers.

5. Discussion

5.1. Influence of Different Contributions of Feature Alignment

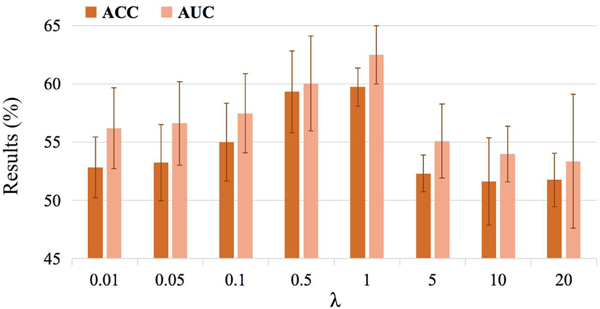
The proposed UFA-Net aims to minimize a hybrid loss that consists of a cross-entropy loss and a maximum mean discrepancy constrained loss (see Eq. 5). To investigate the influence of the maximum mean discrepancy constrained loss, we vary the hyperparameter λ within the range of {0.01,0.05,0.1,0.5,1,5,10}, and record the corresponding results achieved by our UFA-Net in Table 5 and Fig. 4.

Table 5.

Results of the proposed UFA-Net with different values of λ in the task of MDD vs. HC classification. Best results are shown in bold.

λ	ACC (%)	AUC(%)	SEN (%)	SPE (%)	PRE (%)
0.01	52.84±2.61	56.19±3.46	61.08±5.16	44.59±4.44	52.41±2.26
0.05	53.24±3.27	56.61±3.58	60.54±4.86	45.95±6.45	52.90±2.86
0.1	55.00±3.35	57.48±3.40	62.43±4.71	47.57±6.75	54.46±3.01
0.5	59.32±3.51	60.03±4.09	68.11 ±4.15	50.54±10.31	58.41±4.31
1	59.73±1.63	62.50±2.50	69.46±6.43	50.00±9.63	58.49±2.58
5	52.30±1.58	55.08±3.18	39.19± 15.78	65.41 ± 14.11	53.18±2.43
10	51.62±3.74	53.97±2.38	17.57±12.59	85.68±12.04	55.81±13.35

Fig. 4.

Results of the proposed UFA-Net with different values of λ in the task of MDD vs. HC classification in terms of ACC and AUC.

It can be seen from Table 5 and Fig. 4 that the performance of UFA-Net gradually rises with the increase of λ and the overall best results are achieved with λ = 1. But with λ ≥ 5, the classification results are not satisfactory. These results suggest that the proposed UFA-Net can not produce good classification results if we pay more attention to feature alignment by penalizing the maximum mean discrepancy constrained loss more. A potential reason could be that when we use a larger λ, the optimization algorithm will pay less attention to the classification loss, thus making the classification model underfitting.

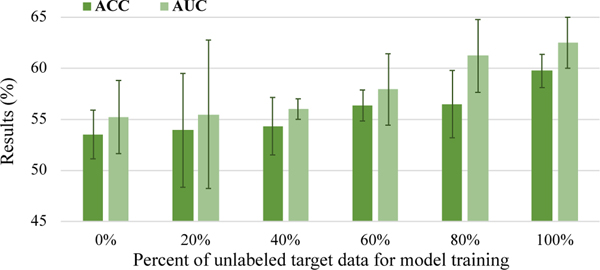
5.2. Influence of Involved Target Sample Size

In the proposed UFA-Net, all unlabeled data (148 subjects) from the target domain are leveraged for model training. Here, we investigate the influence of different target sample sizes on classification performance. Specifically, we train the proposed UFA-Net on all labeled source data and different percentages of unlabeled target data within the range of {0%,20%, · · ·, 100%}. During the inference process, all target samples are used as test data. Results are reported in Table 6 and Fig. 5.

Table 6.

Results of the proposed UFA-Net with different numbers of unlabeled target samples for model training in the task of MDD vs. HC classification. Best results are shown in bold.

Model 1	ACC (%)	AUC (%)	SEN (%)	SPE (%)	PRE (%)
0%	53.51±2.39	55.22±3.59	62.43±4.05	44.59±4.91	53.02±2.18
20%	53.92±5.58	55.49±7.28	52.70±14.17	55.14±12.77	54.20±6.73
40%	54.32±2.82	56.00±1.01	63.78±8.98	44.86±11.95	54.09±3.52
60%	56.35±1.52	57.92±3.50	67.30±6.53	45.41±6.32	55.25±1.32
80%	56.49±3.30	61.21±3.57	66.76±4.41	46.22±8.26	55.61±3.18
100%	59.73±1.63	62.50±2.50	69.46±6.43	50.00±9.63	58.49±2.58

Fig. 5.

Results of the proposed UFA-Net with different percentages of unlabeled target samples for model training in terms of ACC and AUC.

Table 6 suggests that the performance of UFA-Net generally rises as the target sample size increases, and the overall best results are produced when using all target samples. This trend can be visually observed from Fig. 5. This suggests that using more unlabeled target data helps boost classification results. The underlying reason may be that using more target data tends to more reliably reflect true data distribution of the target domain, thereby encouraging UFA-Net to perform more efficient inter-domain feature alignment to improve learning performance.

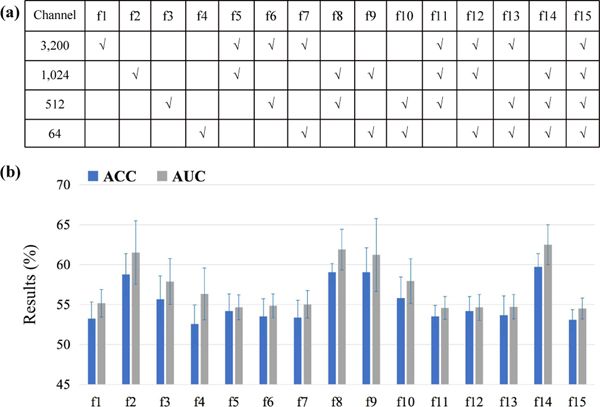
5.3. Influence of Feature Alignment at Different Layers

As shown in Fig. 1, we employ a maximum mean discrepancy constrained module for inter-domain data adaptation based on features generated from three convolutional layers (with 1,024, 512, and 64 channels, respectively). To fully exploit the optimal feature alignment strategy, we perform experiments based on features from permutation and combination of the involved convolutional layers, as shown in Fig. 6 (a), where the tick specifies the corresponding layer for feature alignment. The results with feature alignment at different layers are reported in Fig. 6 (b). The classification models in this group of experiments are based on UFA-Net with fixed parameters, and the only difference is the convolutional layers involved for feature alignment, so the results are comparable.

Fig. 6.

Results of UFA-Net with feature alignment based on fMRI features generated from different convolutional layers in terms of ACC and AUC.

From Fig. 6, we can observe that the model with feature alignment gets better performance (e.g., ACC>58.7%, AUC>61.2%) in four cases (i.e., f2, f8, f9, and f14). Especially, the proposed UFA-Net yields good results when the 1,024-channel layer is involved for feature alignment (i.e., f1, f5, f6, f7, f11, f12, f13, and f15). But when the 3,200-channel layer is involved (i.e., f1, f5, f6, f7, f11, f12, f13, and f15), UFA-Net can not produce satisfactory performance. These results suggest that compared with feature adaptation at low-level feature layers, it is more efficient for UFA-Net to perform feature alignment at high-level semantic feature layers.

5.4. Influence of Brain Atlas

The previous experiments are based on the anatomical AAL atlas for brain ROI definition. To further verify the effectiveness of the proposed UFA-Net, we also employ the Dosenbach atlas with 160 functional ROIs (Dosenbach et al., 2010) for brain parcellation. The classification results are reported in Table 7, where UFA-Net-D denotes the proposed model with Dosenbach and UFA-Net indicates the model with AAL. For comparison, we also report the lower bound of UFA-Net-D, called UFA-Net-D-LB, by training the model on the source data and applying it directly to the target data. The experiments are repeated five times to reduce the bias caused by parameter initialization.

Table 7.

Results of the proposed UFA-Net with different atlases for brain ROI parcellation. Here, the UFA-Net method uses the AAL atlas and the UFA-Net-D uses the Dosenbach atlas. The UFA-Net-D-LB is a degenerated version of UFA-Net-D, without feature alignment.

Model	ACC (%)	AUC (%)	SEN (%)	SPE (%)	PRE (%)
UFA-Net-D-LB	50.27±2.85	50.23±3.94	49.19±8.44	51.35±8.96	50.35±3.48
UFA-Net-D	57.16±2.08	58.23±1.46	62.70±15.09	51.62±11.82	56.41 ± 1.21
UFA-Net	59.73±1.63	62.50±2.50	69.46±6.43	50.00±9.63	58.49±2.58

It can be observed from Table 7, compared with UFA-Net-D-LB, our UFA-Net-D achieves an improvement of 6.89% and 8.00% in terms of ACC and AUC, respectively. This further validates the effectiveness of the proposed feature adaptation strategy in boosting the performance of MDD identification. Besides, UFA-Net-D can produce comparable results with UFA-Net based on the AAL atlas, which implies that the proposed method is not very sensitive to the choice of brain atlases.

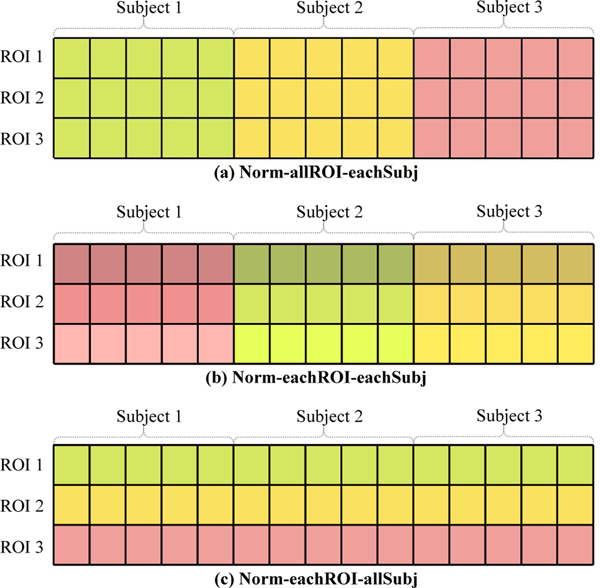
5.5. Influence of Data Normalization

As one of the most important pre-processing steps, fMRI data normalization has a great influence on classification performance. Here, we investigate the influence of three normalization strategies, including (1) Norm-allROI-eachSubj that normalizes all ROIs’ BOLD signal for each subject using z-score standardization, (2) Norm-eachROI-eachSubj that normalizes each ROI’s BOLD signal for each subject, and (3) Norm-eachROI-allSubj that standardizes each ROI’s BOLD signal along all subjects, which is used in the previous experiments. For clarity, we illustrate these three normalization methods in Fig. 7, where three ROIs and three subjects are depicted for simplicity. The classification results of our UFA-Net with the three normalization strategies as well as the raw data (without any normalization) are reported in Table 8.

Fig. 7.

Illustration of three data normalization methods: (a) Norm-allROI-eachSubj that normalizes all ROI signals within one subject, (b) Norm-eachROI-eachSubj that normalizes each ROI signal within one subject, and (c) Norm-eachROI-allSubj that normalizes all subjects for the same ROI. Only three ROIs and three subjects are depicted for simplicity.

Table 8.

Results of the proposed UFA-Net with raw data and three different BOLD signal normalization strategies in the task of MDD vs. HC classification. Best results are shown in bold.

Normalization Strategy	ACC (%)	AUC (%)	SEN (%)	SPE (%)	PRE (%)
Raw Data (without normalization)	52.16±2.11	55.94±2.94	84.59±10.76	19.73±7.77	51.22±1.32
Norm-allROI-eachSubj	55.00±3.88	55.52±3.84	67.03±5.58	42.97±5.76	54.06±3.05
Norm-eachROI-eachSubj	53.65±2.72	55.15±3.16	59.73±6.07	47.57±5.36	53.24±2.48
Norm-eachROI-allSubj (Ours)	59.73±1.63	62.50±2.50	69.46±6.43	50.00±9.63	58.49±2.58

Table 8 suggests that the normalization method we use (i.e., Norm-eachROI-allSubj) achieves the ACC improvement of 4.73% and 6.08%, respectively, compared with the models with Norm-allROI-eachSubj and Norm-eachROI-eachSubj. Note that Norm-eachROI-eachSubj performs the worst among the three approaches, with an average ACC of 53.65%. This result is not surprising since normalizing each ROI’s BOLD signal for each subject tends to neglect individual features which should be informative for differentiating MDD subjects from HCs. In contrast, the Norm-eachROI-allSubj technique we use aims to standardize each ROI’s rs-fMRI data across all subjects, ensuring that the relative ROI signal values across different subjects remain unchanged. This would help preserve the characteristics of the two different groups (i.e., MDD and HC), thus boosting the classification performance.

5.6. Influence of Target Site

To further verify the effectiveness and robustness of our method to the choice of unlabeled target sites, we apply the proposed UFA-Net to another target site (Site-21: 85 MDD patients and 70 HC subjects) of REST-meta-MDD Consortium (Yan et al., 2019), while the source domain remains Site-20. In this group of experiments, the target domain is involved in model training, without the target labels being accessible. The classification results of the proposed UFA-Net and several competing methods are shown in Table 9, from which we can see that our method generally shows superior performance compared with the competing methods, validating the robustness of our method to the choice of target sites.

Table 9.

Results of different methods on another target domain (Site-21) of REST-meta-MDD Consortium (Yan et al., 2019), with Site-20 as the source domain. Best results are shown in bold.

Method	ACC (%)	AUC (%)	SEN (%)	SPE (%)	PRE (%)
BC-SVM-N-G	53.21	50.50	67.44	35.71	56.31
XGBoost	52.56	50.02	68.61	32.86	55.66
DANN	54.74±2.68	52.20±3.25	67.44±8.32	39.14±5.83	57.56±1.66
UFA-Net-LB	51.41±1.43	50.48±0.89	58.14±4.82	43.14±2.91	55.63±0.85
UFA-Net (Ours)	56.15±2.45	56.62±2.68	70.23±7.73	38.86±11.48	58.77±2.58

5.7. Application on Other Brain Diseases

We also apply our method to automated diagnosis of prodromal Alzheimer’s disease, aiming to differentiate patients with early mild cognitive impairment (eMCI) from those with late mild cognitive impairment (lMCI). Specifically, two largest sites from the Alzheimer’s Disease Neuroimaging Initiative (ADNI) database (Jack Jr et al., 2008)² are selected, with Site-2 (with 24 eMCI and 32 lMCI) served as source domain and Site-31 (with 28 eMCI and 25 lMCI) treated as target domain. Similarly, the target domain is involved in model training, with the target labels being inaccessible. The classification results of the proposed UFA-Net and several competing methods are reported in Table 10, from which we can see that our method achieves superior performance compared with the competing methods in terms of all metrics. We find that even though the sample size in each domain is limited (i.e., with only ∼50 subjects), our UFA-Net can still achieve reasonable classification results, which further validates our model’s effectiveness in fMRI-based brain disease diagnosis. Besides, we apply the proposed UFA-Net on the Autism Brain Imaging Data Exchange (ABIDE) initiative³ to identify autism spectrum disorder (ASD) patients from HCs, with results reported in Supplementary Materials.

Table 10.

Classification results of the UFA-Net and several competing methods in the task of eMCI vs. lMCI classification with rs-fMRI data from the ADNI dataset (Jack Jr et al., 2008). eMCI: early mild cognitive impairment; lMCI: late mild cognitive impairment.

Method	ACC(%)	AUC (%)	SEN (%)	SPE (%)	PRE (%)
BC-SVM-N-G	52.83	50.43	64.29	40.00	54.55
XGBoost	50.94	51.21	67.86	32.00	52.78
DANN	49.81±3.50	47.91±4.77	59.29±22.54	39.20±22.11	52.42±3.73
UFA-Net-LB	51.70±5.15	53.14±4.63	62.86±7.35	39.20±9.60	53.78±4.34
UFA-Net (Ours)	55.47±6.38	57.94±8.69	69.29±5.35	40.00±13.62	56.89±5.70

5.8. Influence of Attention Technique

To investigate the influence of attention mechanism on the diagnosis performance, we conduct ablation studies by comparing our UFA-Net with its degraded version without attention (called UFA-Net w/o Att). The classification results are shown in Table 11. From the table, we can observe that there exists no significant difference between UFA-Net models with and without the attention strategy. But our learned attention mask can help explicitly localize the disease-related functional connectivities, and the visualized discriminative connectivities and associated ROIs (see Fig. 2) can facilitate the understanding of the brain functional mechanism of MDD patients.

Table 11.

Results of the proposed UFA-Net with and without attention mechanism in the task of MDD vs. HC classification.

Method	ACC (%)	AUC (%)	SEN (%)	SPE (%)	PRE (%)
UFA-Net w/o Att	59.73±1.32	62.37±2.82	70.00±6.75	49.46±8.36	58.28±1.81
UFA-Net	59.73±1.63	62.50±2.50	69.46±6.43	50.00±9.63	58.49±2.58

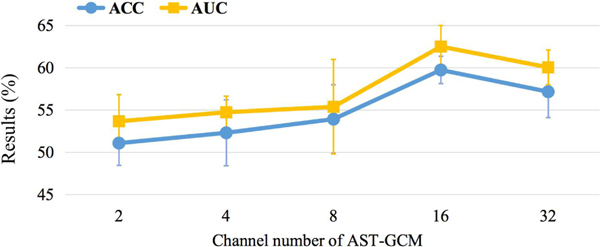
5.9. Influence of Channel Numbers

As mentioned in Section 3.2.2, each ST-GC unit produces 16-channel feature outputs. To investigate the influence of channel numbers on MDD classification performance, we vary the channel number within the range of {2,4,8,16,32}, and the prediction results are given in Table 12 and Fig. 8. We can observe that the proposed UFA-Net suffers from performance degradation when the channel number is small, e.g., {2,4,8}. The underlying reason may be that with fewer learnable parameters, the trained model is prone to underfitting, thereby the relationship between the input features and diagnostic label cannot be accurately modeled, resulting in unsatisfactory performance. If the number of learnable parameters is very large (e.g., with 32 channels), the performance of UFA-Net is not that good.

Table 12.

Results of the proposed UFA-Net with different ST-GC channels in the task of MDD vs. HC classification. Best results are shown in bold.

Channel	ACC (%)	AUC (%)	SEN (%)	SPE (%)	PRE (%)
2	51.08±2.65	53.66±3.17	54.32±7.57	47.84±9.99	51.22±2.35
4	52.30±3.91	54.73±1.90	58.92±8.49	45.68±15.56	53.00±4.78
8	53.92±4.04	55.37±5.58	64.59±9.18	43.24±11.87	53.49±3.39
16	59.73±1.63	62.50±2.50	69.46±6.43	50.00±9.63	58.49±2.58
32	57.16±3.04	60.04±2.04	68.92±9.00	45.41±11.10	56.03±2.79

Fig. 8.

Results of the proposed UFA-Net with different ST-GC channels in the task of MDD vs. HC classification in terms of ACC and AUC.

5.10. Limitations and Future Work

Several limitations need to be addressed in the future. First, the proposed model is only trained on one single source domain and adapted to the target domain without taking advantage of multiple source domains. In the future, we will explore utilizing diverse data from multiple source domains, which is expected to further improve learning performance. Second, we only learn brain functional connectivity features based on one single brain atlas (i.e., AAL or Dosenbach), while multi-scale brain ROI partition provides coarse-to-fine information on brain functional activity. It is interesting to integrate functional connectivity features learned from multi-scale brain atlases to further boost classification performance. Third, current work only investigates functional characteristics while brain structural information (e.g., T1 and diffusion tensor imaging) may also help automated MDD diagnosis. Future work will seek to integrate complementary features from both anatomical and functional modalities to further improve the learning performance. In addition, only neuroimaging data are leveraged in the current work, while demographic information (e.g., age, gender, education, and clinical scores) may also be essential for brain disease diagnosis. We will explore both non-imaging and imaging characteristics for automated MDD identification in the future.

6. Conclusions

We propose a discrepancy-based unsupervised cross-domain fMRI adaptation framework for automated MDD identification. We first capture spatio-temporal fMRI features of source and target data via an attention-guided graph convolution module. A maximum mean discrepancy constrained module is then designed for feature alignment between labeled source and unlabeled target domains. Experiments on 681 subjects with rs-fMRI data suggest the superior performance of the proposed method. The proposed method helps localize disease-associated functional connectivity abnormalities, which would facilitate fMRI-based MDD analysis in clinical practice.

Highlights.

1. A novel discrepancy-based unsupervised cross-domain fMRI adaptation framework is developed for major depressive disorder (MDD) diagnosis. To the best of our knowledge, this is one of the first attempts to investigate cross-site fMRI adaptation for MDD analysis.

2. A maximum mean discrepancy constrained module is introduced for fMRI feature alignment between labeled source and unlabeled target domains, and these features are automatically learned by an attention-guided spatio-temporal graph convolution module.

3. The proposed method helps localize disease-related brain regions and functional connectivity abnormalities based on fMRI time series. This would facilitate fMRI-based MDD analysis in clinical practice.