Comparison of nonlinear curves and surfaces

Abstract

Estimation of nonlinear curves and surfaces has long been the focus of semiparametric and nonparametric regression analysis. What has been less studied is the comparison of nonlinear functions. In lower-dimensional situations, inference typically involves comparisons of curves and surfaces. The existing comparative procedures are subject to various limitations, and few computational tools have been made available for off-the-shelf use. To address these limitations, two modified testing procedures for nonlinear curve and surface comparisons are proposed. The proposed computational tools are implemented in an R package, with a syntax similar to that of the commonly used model fitting packages. An R Shiny application is provided with an interactive interface for analysts who do not use R. The new tests are consistent against fixed alternative hypotheses. Theoretical details are presented in an appendix. Operating characteristics of the proposed tests are assessed against the existing methods. Applications of the methods are illustrated through real data examples.

1. Introduction

An essential task in nonparametric and semiparametric regression is to estimate nonlinear functions for depiction of relations between independent and dependent variables. In lower-dimensional situations, the functions are often expressed as smooth curves and surfaces [1]. Various smoothing techniques have been developed for the estimation of nonlinear functions. Commonly used methods include local polynomial models [2], wavelets [3], smoothing splines [4, 5], and various types of penalized regression splines [6, 7, 8, 9]. Most of these estimation methods can be easily implemented in common computational platforms, giving analysts much flexibility for curve and surface estimation. What has been less studied is the inference concerning nonlinear functions, and there is a dearth of computational tools for practical use. A question of general interest is whether a specific nonparametric smoother, when applied to different comparison groups, gives the same function.

To address the question above, we review the existing literature on curve and surface comparisons, and present two L₂-based testing procedures with related theoretical and numerical justifications. Our procedures are based on B-splines, although the formulation of the test statistics could be extended to other smoothers. We put forward an R package, which can be accessed either directly from within R, or through an interactive R-Shiny interface; the latter allows analysts who do not use R to perform the desired comparisons. To illustrate the use of the proposed methods, we present two real data examples.

2. Existing methods for curve and surface comparison

Comparison of smooth curves can be formalized as a test of the following hypothesis H₀ : g₁(x) = g₂(x) = ⋯ = g_I(x), $\forall x\in ℝ\text{vs}{H}_1:g_i\left(x\right)\ne g_j\left(x\right)$ for some i, j ∈ {1, … , I}, where i and j indicate different comparison groups. In the situation of $x\in {ℝ}^2$, g_i(x) and g_j(x) are surface functions. The concept can be extended to higher-dimensional functions, although visualization of higher-dimensional functions becomes more difficult. In this paper, we restrict the discussion to lower-dimensional situations, and we write the underlying model as Y = g_i(x) + ϵ. We use capital letters Y and X to indicate the random response and independent variables, and their lower-case counterparts x and y to indicate the observed values of the corresponding random variables.

Early work on this problem started almost three decades ago. One approach is to frame the problem in a regression setting, where a modified version of the Kolmogorov-Smirnov test could be used to compare the regression curves [10]. Another approach is to transform the nonparametric curves to reduce the comparison to a test of limited dimensional parameters within the transformation matrix [11]. Alternatively, wavelet methods have been used to compare density functions [12]; the methods are especially suitable for comparing higher frequency local features. Many of these methods, however, require the curves to have the same design points, i.e., all functions must be evaluated at the same x values. To remedy, Kulasekera (1995) fitted kernel-based regression models and proposed tests based on the weighted average of partial sum of squares of the quasi-residuals and error variances [13]. But simulations suggest that these tests tend to be overly sensitive to bandwidth selection. There are also specialized tests for parallelism among the curves [14, 15].

In this section, we briefly review the methods that are most frequently used in analytical practice.

2.1. Nonparametric Analysis of Covariance (ANCOVA)

Young and Bowman (1995)[16] described a method for testing the equality of two or more smooth curves, under the model Y_ij = g_i(x_ij) + ϵ_ji, where ϵ_ij ~ N(0, σ²), for i = 1, 2, … , I, j = 1, … , n_i. The test has a homoscedastic assumption, i.e., the error variance remains constant across all I groups.

Young and Bowman used a kernel-based smoothing method to approximate g_i. Assuming that h_i is the bandwidth for the ith regression function, they proposed to estimate g_i with

$${\widehat{g}}_i\left(x\right)=\frac{{\sum }_{j=1}^{n_i}K\left(\left(x-x_{ij}\right)/h_i\right)y_{ij}}{{\sum }_{j=1}^{n_i}K\left(\left(x-x_{ij}\right)/h_i\right)},$$ (1)

which is sometimes referred to as the Nadaraya-Watson estimator of g_i.

Under the null hypothesis, one could obtain a common regression function by combining data from all groups

$$\widehat{g}\left(x\right)=\frac{{\sum }_{i=1}^I{\sum }_{j=1}^{n_i}K\left(\left(x-x_{ij}\right)/h\right)y_{ij}}{{\sum }_{i=1}^I{\sum }_{j=1}^{n_i}K\left(\left(x-x_{ij}\right)/h\right)},$$ (2)

where h is the common bandwidth for estimating g.

The test statistic that Young and Bowman proposed is analogous to the one-way ANOVA,

$$T_1=\frac{\sum _{i=1}^I\sum _{j=1}^{n_i}{\left[\widehat{g}\left(x_{ij}\right)-{\widehat{g}}_i\left(x_{ij}\right)\right]}^2}{{\widehat{\sigma }}^2},$$ (3)

where ${\widehat{g}}_i$ and $\widehat{g}$ are the group-specific and common curve estimators, and ${\widehat{\sigma }}^2$ is the pooled variance. To estimate σ², one uses ${\widehat{\sigma }}^2=\frac{1}{N-I}{\sum }_{i=1}^I\left(n_i-1\right){\widehat{\sigma }}_i^2$, where $N={\sum }_{i=1}^I{n}_i$. Similarly, the group-specific variance is estimated as

$${\widehat{\sigma }}_i^2=\frac{1}{2\left(n_i-1\right)}\sum _{j=1}^{n_i-1}{\left(y_{i,\left[j+1\right]}-y_{i,\left[j\right]}\right)}^2.$$

This test has been extended to comparisons of surface functions [17].

The construction of the test is intuitive, and its implementation straight-forward. The equal variance assumption, however, can be overly restrictive in some analytical situations. Additionally, when the explanatory variable x_ij takes different values in the comparison groups, the power of the test often drops precipitously because the biases can no longer be canceled out under H₀; see Tables 1– 3 in Young and Bowman (1995)[16].

Table 1:

Summary of the existing methods

Author(s), Methods	Same x(s)	Correlation	>2 Groups	Curve/Surface	Additional Comments
Bowman (2006)[17]:	Y	N	N	Curve/Surface	(+) Simple to implement and understand as a derivation from ANOVA test; (−) Assume equal variance across groups.
Dette & Neumeyer (2001)[19], Pardo-Fernandez & Van Keilegom (2007)[21], Wang & Ye (2010)[23]:	N	N	Y	Curve/Surface	(+) Demonstrated asymptotic normality of all three kernel-based statistics under H0; Recommended wild bootstrap when studying finite samples.
Zhang & Lin (1998)[24]:	Y	Y	N	Curve	(+) Spline-based semiparametric additive model; (−) χ2 approximation can be biased with different covariate values.
Wang & Ye (2010)[23]:	N	Y	Y	Curve/Surface	(+) Able to adjust for spatial correlation; (−) Larger bias in estimating regression surface hence decreased power.
Kulasekera (1995)[13]:	N	N	N	Curve	(+) Low computational demand; (−) Low power when curve functions are similar.
Park, Hannig,& Kang (2014)[18]:	N	N	Y	Curve	(+) A visualization tool to present differences between curves across multiple locations and scales; (−) Type 1 error rate below nominal level; relatively low power

Table 3:

P-values for weight growth curves and weight growth surfaces for different race and sex groups

Endpoints vs predictor(s)	Group effect	Subset data	T spline	T 4	T 3	T 2
Weight vs. Age	Sex	Black	0.08	0.16	0.55	<0.01
		White	0.48	0.18	0.69	0.28
	Race	Boys	0.41	0.09	0.69	0.2
		Girls	<0.01	0.01	0.96	<0.01
Weight vs. Age & Height	Sex	Black	0.16	0.65	0.66	0.49
		White	0.49	0.55	0.55	0.77
	Race	Boys	0.42	0.42	0.46	0.35
		Girls	0.34	0.19	0.91	0.06

More recently, Park and colleagues considered a similar ANOVA type test statistic for multiple x values with a given bandwidth [18]. They obtained an empirical distribution for the maximum of the pointwise test statistics for controlling multiplicity. A visualization tool has been developed to show differences between curves at multiple locations. But simulation studies suggest that the test has type I error rates far below the nominal level, and very low power; see Table 1 of Park et al [18].

2.2. Kernel-based nonparametric methods

Dette and Neumeyer (2001) proposed another set of tests, all based on kernel smoothing techniques [19]. Expressing the curves as Y_ij = g_i(x_ij) + ϵ_ij(x_ij), where i = 1, 2, … , I, j = 1, … , n_i, the authors introduced heteroscedastic errors ${ϵ}_{ij}\left(x_{ij}\right)~N\left(0,{\sigma }_i^2\right)$ into the model. The main hypothesis remains the same, H₀ : g₁ = g₂ = ⋯ = g_I vs H₁ : g_i ≠ g_j for some i, j ∈ {1, … , I}.

The tests are subject to the following conditions: (1) The variances σ_i(·) are continuous functions; (2) the design points x_ij satisfy ${\int }_0^{x_{\mathrm{i,j}}}{r}_i\left(x\right)dx=\frac{j}{n_j}$ for a density function r_i, where j = 1, … , n_i, and i = 1, … , I; (3) the regression functions g(·) are sufficiently smooth, i.e., ≥ 2 times continuously differentiable in the supporting space. And the Nadaraya-Watson estimators ${\widehat{g}}_i$ and $\widehat{g}$ are as previously defined.

One test (T₂) compares the group-specific error variances against that of the combined sample, in a way that is analogous to one-way ANOVA

$$T_2={\widehat{\sigma }}^2-\frac{1}{N}\sum _{i=1}^I{n}_i{\widehat{\sigma }}_i^2.$$ (4)

The second test (T₃) directly assesses the distance between the group-specific curves and a common curve at x_ij, assuming that x_ij remain exactly the same across the groups,

$$T_3=\frac{1}{N}\sum _{i=1}^I\sum _{j=1}^{n_i}{\left[\widehat{g}\left(x_{ij}\right)-{\widehat{g}}_i\left(x_{ij}\right)\right]}^2.$$ (5)

The third test (T₄) summarizes all pairwise L₂-distances of the estimated individual grooup curves,

$$T_4=\sum _{i=1}^I\sum _{j=1}^{i-1}\int {\left[{\widehat{g}}_i\left(x\right)-{\widehat{g}}_j\left(x\right)\right]}^2{w}_{ij}\left(x\right)dx,$$ (6)

where w_ij(·) are positive weight functions. Asymptotic normality of the test statistics has been established under the null and fixed alternatives.

The above tests have been extended to comparison of two regression curves with different design points and heteroscedastic variances [20]. For comparison of two curves, the authors proved by using the empirical process theory that the two marked empirical processes converged to a centered Gaussian process at a rate of N^−1/2 under the null; while under the alternative, the means of the two processes do not converge to zero. Hence, tests could be constructed based on either functions of the integrated squared residuals or the supremum of the absolute residuals of these two processes.

A practically important extension of Neumeyer and Dette’s methods is the comparison of multiple curve functions [21]. These tests have also been extended to compare surface functions. Since the rates of convergence of the test statistics are slower [22], and the wild bootstrap procedure is consistent under more relaxed conditions, analysts often calculate p-values from the distribution of the test statistic under H₀ using a wild bootstrap procedure [23].

2.3. Additive model-based tests

Zhang and Lin (2000) [24] considered testing the equivalence of two nonparametric functions in an additive mixed model for longitudinal data

$$Y_{ijk}=g_i\left(x_{ijk}\right)+{\mathbf{s}}_{ijk}^T{\mathbf{\alpha }}_i+{\mathbf{Z}}_{ijk}^T{b}_{ij}+{ϵ}_{ijk},$$ (7)

where Y_ijk is the response from the jth subject in the ith group at the kth assessment, and α_i is a p × 1 vector associated with covariates s_ijk.

To test hypothesis H₀ : g₁ = g₂ vs. H₁ : g₁ ≠ g₂, the authors suggested the following test statistic

$$G\left\{{\widehat{g}}_1\left(x\right),{\widehat{g}}_2\left(x\right)\right\}={\int }_{T_1}^{T_2}\left\{{\left[{\widehat{g}}_1\left(x\right)-{\widehat{g}}_2\left(x\right)\right]}^2\right\}dx,$$ (8)

where ${\widehat{g}}_1$ and ${\widehat{g}}_2$ are estimated by maximizing the penalized log-likelihood function.

The penalized likelihood under the semiparametric additive mixed model for an individual group is $l\left(g_i,{\alpha }_i;y\right)-\frac{{\lambda }_i}{2}\int {\left[g_i^{\prime \prime }\left(x\right)\right]}^{2}dx$, where λ_i is the parameter that controls the smoothness of function g_i(x). Note that the test statistic (8) is also an L₂-based distance measure, as that in (6). Expressing G in Equation (8) as a quadratic function of y, Zhang and Lin approximated the distribution of $G\left\{{\widehat{g}}_1\left(x\right),{\widehat{g}}_2\left(x\right)\right\}$ with a scaled χ² distribution using the moment matching technique.

We summarize the tests reviewed in Table 1, which highlights the key features of each method.

3. Curve comparison in semiparametric regression

In a low-dimensional regression analysis, comparing nonlinear effects amounts to a comparison of nonlinear curves and surfaces. As described in Table 1, the existing methods are often overly restrictive in their accommodation of heterogeneity and design points. For example, when we compare two nonlinear functions g₁(x) and g₂(x), it is rather unrealistic to expect the two functions be evaluated at the exact same x values. Furthermore, if the functions are indeed different, it would not be reasonable to expect the two functions to have the same variance. These are the features that the existing methods and analytical software have not accommodated adequately.

To remedy, we propose a testing procedure in the usual context of semiparametric regression. For the convenience of discussion, we consider a comparison of curve functions g_i(x_ij), where x_ij denotes the value of independent variable of the jth subjects in the ith group. We are interested in testing hypothesis g₁ = g₂ = ⋯ = g_I. We note that the test can be extended to compare higher dimensional functions, although visualization may be difficult.

In order to test the above hypothesis, one needs to estimate the functions, g₁,g₂,…, g_I, as well as g. Most of the existing methods are developed based on kernel estimates. In practice, however, many analysts prefer various forms of regression splines, with or without smoothness penalty. In this paper, all theoretical results are derived under B-spline estimates. For all practical purposes, choices of spline basis functions are often less consequential. Here for curve comparison, we write the model as Y_ij = g_i(x_ij) + ϵ_ij, where ${ϵ}_{ij}~N\left(0,{\sigma }_i^2\right)$, and we write the group-specific function g_i as a B-spline function, i.e., $g_i\left(x\right)={\sum }_{k=1}^{K_n+m}{\gamma }_k{B}_k^m\left(x\right)$, where K_n is the number of internal knots with K_n = O(n^v), m is the order of the B-spline with m ≥ 1, ${\left\{{\gamma }_k\right\}}_{k=1}^{K_n+m}$ is the set of B-spline coefficients, and $\left\{B_k^m\left(x\right):x\in \left[a,b\right]\right\}$ are B-spline basis functions. For higher dimensional functions g_i(x₁, x₂, … , x_d), one could use tensor products, radial, or thin-plate splines [25][26][27].

3.1. Test statistics and comparison procedures

An intuitive way to compare two functions is to measure the distance between them. The L₂ norm is a commonly used distance measure. As described previously, both Zhang and Lin (2000) and Dette and Neumeyer (2003) used the L₂ norm in the construction of their test statistics. Herein, we reexamine the test statistic

$$T_{\mathit{\text{spline}}}=\frac{1}{N}\sum _{1\le i<m\le I}\sum _{j=1}^{n_i}{\left[{\widehat{g}}_i\left(x_{ij}\right)-{\widehat{g}}_m\left(x_{ij}\right)\right]}^2,$$

under B-spline estimates of ${\widehat{g}}_i$ and ${\widehat{g}}_m$ for testing the hypothesis H₀ : g₁ = g₂ = ⋯ = g_I vs H₁ : g_i ≠ g_j for some i, j ∈ {1, … , I}. Theoretical properties of the test statistic are examined in Section 3.1.2.

In the absence of an asymptotic normal distribution, however, one has to devise a method to approximate the distribution of the test statistic under the null hypothesis. In the following section, we demonstrate how such an approximation can be done through a resampling procedure. Specifically, we show how to ascertain p values for the test statistic from a wild bootstrap procedure.

3.1.1. A wild bootstrap-based comparison method

For the standard linear regression models, it is usually sufficient to draw bootstrap samples from centralized residuals, because the errors are homoscedastic [28]. In the one dimensional case, the underlying model can be written as Y_ij = g_i(x_ij) + ϵ_ij, where ${ϵ}_{ij}~N\left(0,{\sigma }_i^2\right)$. We present g as a curve function here, although the method can be easily extended to higher dimensional situations.

To accommodate error heteroscedasticity, we consider a wild bootstrap procedure, which assures that the bootstrap error terms possess properties that are similar to those of the actual errors [29]. Another alternative approach is to use pairs bootstrapping, in which the analyst directly resamples from the joint empirical distribution function of Y_i and x_i, which are the vectors of the response and independent variables respectively. The computational burden of pairs bootstrap, however, tends to be greater especially if the dimension of x_i is high [28].

Wild bootstrap has been used to resample the residuals of nonparametric regression models, as suggested by Härdle and Mammen (1993) [30], and Mammen (1993) [31]. The essence of wild bootstrap is to express the regression function as a conditional expectation of the observed response variable, i.e. $E\left(Y_i^{\ast }|X_i=x_i\right)=g\left(x_i\right)$, where $Y_i^{\ast }$ is the bootstrap data. Since this method uses a single residual ${\widehat{ϵ}}_i$ to estimate the conditional distribution l(Y_i − g(x_i)|X_i = x_i) of an arbitrary distribution (${\widehat{F}}_i$ in the following), it is often referred to as the wild bootstrap.

Let V_i be a random variable following a two-point distribution ${\widehat{F}}_i$ such that $E_{{\widehat{F}}_i}\left(V_i\right)=0$, $E_{{\widehat{F}}_i}\left(V_i^2\right)=1$, and $E_{{\widehat{F}}_i}\left(V_i^3\right)=1$. We define random independent quantities ${ϵ}_i^{\ast }=V_i{\widehat{ϵ}}_i~{\widehat{F}}_i$, and use $\left(X_i,Y_i^{\ast }=\widehat{g}\left(x_i\right)+{ϵ}_i^{\ast }\right)$ as the bootstrap observations. We then create a new bootstrap test statistic T*.

With the bootstrap samples, for a test at level α, the null hypothesis will be rejected if T is greater than the corresponding quantile of the bootstrap distribution of the test statistic T*, i.e. $T>T_{\left[B\left(1-\alpha \right)\right]}^{\ast }$, where $T_{\left[B\left(1-\alpha \right)\right]}^{\ast }$ is the ith order value of the bootstrap statistic T*. Härdle and Mammen (1993)[30] showed that under the null hypothesis, T* estimated the distribution of T consistently, since the regression function with bootstrap data g*(·) had mean g(·) for nonlinear models under the standard regularity conditions.

Using the wild bootstrap method, we propose the following procedure:

• Step 1: Estimate function g_i(x) with ${\widehat{g}}_i\left(\mathbf{x}\right)$, i = 1, 2, … , I, and compute the test statistic

  $$T_{\mathit{\text{spline}}}=\frac{1}{N}\sum _{1\le i<m\le I}\sum _{j=1}^{n_l}{\left[{\widehat{g}}_i\left(x_{ij}\right)-{\widehat{g}}_m\left(x_{ij}\right)\right]}^2.$$

• Step 2: Estimate the common function $\widehat{g}\left(\mathbf{x}\right)$ from the combined sample and calculate the residuals ${\widehat{ϵ}}_{ij}=y_{ij}-\widehat{g}\left(x_{ij}\right)$.

• Step 3: For each x_ij, draw a bootstrap residual ${ϵ}_{ij}^{\left(b\right)}$, for b = 1, 2, … , B, where B is the number of bootstrap samples, from the two-point distribution with probability mass points $\frac{1-\sqrt{5}}{2}{\widehat{ϵ}}_{ij}$ and $\frac{1+\sqrt{5}}{2}{\widehat{ϵ}}_{ij}$, occurring with probabilities $\frac{5+\sqrt{5}}{10}$ and $\frac{5-\sqrt{5}}{10}$ respectively, so that $E\left({ϵ}_{ij}^{\left(b\right)}\right)=0$, $E\left({ϵ}_{ij}^{\left(b\right)2}\right)={\widehat{ϵ}}_{ij}^2$ and $E\left({ϵ}_{ij}^{\left(b\right)3}\right)={\widehat{ϵ}}_{ij}^3$.

• Step 4: Generate a bootstrap sample $\left(x_{ij},Y_{ij}^{\left(b\right)}\right)$ from $Y_{ij}^{\left(b\right)}=\widehat{g}\left({\mathbf{x}}_{ij}\right)+{ϵ}_{ij}^{\left(b\right)}$.

• Step 5: From this sample, estimate the bth bootstrap regression function ${\widehat{g}}_i^{\left(b\right)}$, and calculate the test statistic T^(b) as in the original T_spline calculation.

• Step 6: Repeat Step 3 to 5 B times, and use the B generated values of the test statistics, $T_{\mathit{\text{spline}}}^{*}=\left(T^{\left(1\right)},T^{\left(2\right)},\dots ,T^{\left(B\right)}\right)$, to determine the quantiles of the distribution of the test statistic. For a test at significance level α, the null hypothesis is rejected if T_spline is greater than the corresponding (1 − α)th quantile of the bootstrap distribution of $T_{\mathit{\text{spline}}}^{*}$.

3.1.2. Consistency of the test against fixed alternatives

In this section we show that the proposed test is consistent against any fixed alternatives. We also provide the optimal number of internal knots for the B-spline that leads to the best possible rate of convergence. We first rewrite the model in a slightly more general form; here we use X instead of x to emphasize the random nature of the independent variable.

We write the true model as follows

$$Y_j=g_0\left(X_j\right)+{ϵ}_j=g_0\left(X_j\right)+\sigma e_j,$$

where g₀ is an unknown function of interest, (Y_j, X_j), j = 1, … , n, are i.i.d. random variables independent of the error term e_j ~ N(0, 1). For simplicity and without loss of generality, we assume that the covariate $X_j\in \mathbb{X}$ a.s., where $\mathbb{X}=\left[0,1\right]$. As defined, $\mathbb{X}$ is a compact subset in $ℝ$.

As previously described, a B-spline estimate of $g\left(x\right)={\sum }_{k=1}^{K_n+m}{\gamma }_k{B}_k^m\left(x\right)$ can be achieved by minimizing the objective function

$$\frac{1}{n}\sum _{j=1}^n{\left[Y_j-g\left(X_j\right)\right]}^2,$$

or, equivalently, by maximizing

$${\mathbb{M}}_n\left(g\right)\equiv {\mathbb{P}}_n{m}_g=2{\mathbb{P}}_n\left(g-g_0\right)e-{\mathbb{P}}_n{\left(g-g_0\right)}^2,$$

where ${\mathbb{P}}_n{m}_g$ denotes the empirical process indexed by the function m_g, i.e.

$${\mathbb{P}}_n{m}_g=\frac{1}{n}\sum _{j=1}^n{m}_g\left(X_j\right)=-\frac{1}{n}\sum _{j=1}^n{\left[Y_j-g\left(X_j\right)\right]}^2.$$

Direct maximization of the above objective function over the full infinite-dimensional parameter space $\mathcal{G}$ may lead to inconsistant estimates[32]. There-fore, one has to use the sieve M-estimation framework by considering the spaces of B-spline functions

$${\mathcal{G}}_n\left(D_n,K_n,m\right)=\left\{g_n:g_n\left(x\right)=\sum _{k=1}^{K_n+m}{\gamma }_k{B}_k^m\left(x\right)\in S_n\left(D_n,K_n,m\right),x\in \left[0,1\right]\right\},$$

where $D_n=\left\{d_1,\dots ,d_{K_n}\right\}$ is a set of partition points for the set [0, 1], K_n is the number of internal knots with K_n = O(n^v), m is the order of the B-spline with m ≥ 1, ${\left\{{\gamma }_k\right\}}_{k=1}^{K_n+m}$ is the set of the unknown coefficients or control points for the B-spline, $\left\{B_k^m\left(x\right):x\in \left[a,b\right]\right\}$ are the basis functions, and S_n(D_n, K_n, m) is the space of polynomial splines on a partition D_n with K_n internal knots and of order m. Then, the sieve estimator ${\widehat{g}}_n$ of g₀ satisfies

$${\mathbb{M}}_n\left({\widehat{g}}_n\right)\ge {\mathbb{M}}_n\left(g\right)\text{for all}g\in {\mathcal{G}}_n,$$

that is ${\widehat{g}}_n$ maximizes $g\mapsto {\mathbb{M}}_n\left(g\right)$ over the sieve space ${\mathcal{G}}_n\left(D_n,K_n,m\right)$.

For simplicity of presentation, we consider the special case of the two-sample comparison. We assume the following regularity conditions:

• C1. The error e_j has a distribution with zero mean and sub-exponential tails, i.e., tails bound by the supremum of an empirical process. Also, e and the covariate X are independent.

• C2. The parameter space ${\mathcal{G}}_i\ni g_{0,i}$, i = 1, 2, contains functions uniformly bounded by C ≥ 1/2 on [0, 1], with bounded pth derivatives, for fixed p ≥ 1, with the first derivative being continuous.

• C3. The number of internal knots satisfies K_n = O(n^v), such that

  $$\underset{1\le k\le K_n+1}{\text{max}}\left\{d_k-d_{k-1}\right\}=O\left(n^{-v}\right).$$
• C4. The sample sizes of the two groups satisfy

  $$\frac{n_1}{n_1+n_2}\to \lambda \in \left(0,1\right),$$

  as min(n₁, n₂) → ∞.

Theorem 1. Assuming conditions C1-C4 hold, we consider a wild-bootstrap procedure that of level α asymptotically. Then, the proposed test is consistent against any fixed alternative hypothesis: If π_n(θ_δ) is the power function of the test under the fixed alternative hypothesis θ_δ, then π_n(θ_δ) → 1 as n → ∞.

A sketch of the proof is provided in Appendix A. Even though the proposed test is, by Theorem 1, consistent against any fixed alternative hypothesis, the asymptotic distribution of the test statistic is difficult to derive. The difficulty stems from the fact that the convergence rate of the B-spline estimator of g₁ and g₂ is

$$d\left({\widehat{g}}_{n_i,i},g_{0,i}\right)=O_p\left(n^{\frac{p}{1+2p}}\right),i=1,2,$$

where d(g₁, g₂) = {E[g₁(X) − g₂(X)]²}^1/2. Note that the above rate is the optimal convergence rate for nonparametric regression and is achieved if one sets v = 1/(1 + 2p). This convergence rate is slower than the usual $\sqrt{n}$ rate for parametric models, even though it is the optimal rate in nonparametric regression.

In the absence of an analytically derived asymptotic distribution, we assessed the performance of the wild-bootstrap procedure through extensive simulations. Results of the simulation experiments are presented in Section 5.

3.1.3. Extending the testing procedure to correlated data

The same testing procedures can be modified and extended to the analysis of correlated data. A key requirement for the modification is the preservation of the correlation structure that exists within each subject. The following algorithm is a natural extension and it performs a Cholesky decomposition on the estimated covariance structure [33]. Combining with the estimated regression functions, we generate the bootstrap sample $Y_{ijk}^{\left(b\right)}$.

The algorithm is described below.

• Step 1: Obtain group-specific estimates ${\widehat{g}}_i\left(\mathbf{x}\right)$ of function g_i by using semiparametric mixed effect models, and then compute the test statistic T_splcorr.

• Step 2: Obtain a common regression function estimate $\widehat{g}\left(\mathbf{x}\right)$ for the combined sample.

• Step 3: For i = 1, … , I, obtain the group-specific covariance matrix estimate ${\widehat{\mathbf{R}}}_i$ from the fitted group-specific model and ascertain the residuals ${\widehat{\eta }}_i=\left({\widehat{\eta }}_{i11},{\widehat{\eta }}_{i12},\dots ,{\widehat{\eta }}_{in{n}_i}\right)$.

• Step 4: Perform a Cholesky decomposition on ${\widehat{R}}_i$ so that ${\widehat{R}}_i={\widehat{L}}_i{\widehat{L}}_i^T$, where ${\widehat{L}}_i$ is a lower triangular matrix. We then obtain

  $${\widehat{\mathbf{e}}}_i=\left({\widehat{e}}_{i11},{\widehat{e}}_{i12},\dots ,{\widehat{e}}_{in{n}_i}\right)={\widehat{\mathbf{L}}}_i^{-1}{\widehat{\eta }}_i;$$

  and calculate the “whitened” residuals ${\tilde{\mathbf{e}}}_i={\widehat{\mathbf{e}}}_i-\frac{1}{n_i}{\sum }_{j=1}^{n_i}{\widehat{\mathbf{e}}}_i$.

• Step 5: Draw a random sample from the “whitened” residuals ${\tilde{\mathbf{e}}}_i$ and calculate ${\tilde{\eta }}_i^{\left(b\right)}={\widehat{\mathbf{L}}}_i{\tilde{\mathbf{e}}}_i$. We use $Y_{ijk}^{\left(b\right)}=\widehat{g}\left(x_{ijk}\right)+{\tilde{\eta }}_{ijk}^{\left(b\right)}$ as the bootstrap sample.

• Step 6: Calculate the test statistic T^(b) with the bootstrap sample. Repeat Steps 3 to 5 B times to construct an empirical distribution of the statistic with bootstrap samples, and then calculate the p value from the tail area of the empirical distribution.

4. Software development

We published an R package gamm4.test in CRAN to make the proposed testing procedures available to practitioners. The two main functions are gam.grptest for comparisons of nonlinear functions with cross-sectional data, and gamm4.grptest for comparisons involving correlated data. Key features of this package are:

1. It utilizes a syntax that is consistent with mgcv and gamm4, two packages that are often used for fitting semiparametric regression models. Users familiar with those packages can perform comparisons with gam.grptest and gamm4.grptest.

2. The package performs parallel computing with an automatic detection of thenumbers of available CPU cores for enhanced computational efficiency.

3. The R package includes a data visualization function plot.gamtest that allows users to visually examine the fitted curves and surfaces. The graphics are produced by the R package plotly. With option type = plotly.persp, the users can create 3-dimensional interactive plots. Finally, setting the option test.statistic = TRUE generates the empirical distribution of the test statistic under the null hypothesis of equal regression functions.

Computational efficiency of gamm4.test in the analysis of the example data in the package was assessed on a computer with Intel(R) Core(TM) i5–3470, CPU @3.20GHz, 64-bit operating system, and 4 CPU cores. The computing time is summarized in Table 2.

Table 2:

Average run times and standard errors in seconds over 20 runs of the proposed methods for each of the examples in the package, with and without using the parallel computing

Data	Functions	Obs per group	Time (parallel)	Time (no parallel)
cross-sectional	curve	(474,465)	9.6(0.2)	9.1(0.2)
	surface	(474,465)	14.8 (0.2)	23.5(0.6)
correlated	curve	(1873,1713)	86.4(0.6)	204.5(1.6)
	surface	(1873,1713)	664.6(13.6)	1749.0 (30.3)

To enhance the usability of the testing methods, we also created an interactive R Shiny interface for the gamm4.test package. This interface allows analysts that do not use R to access the testing procedure through a web link. See https://heather.shinyapps.io/shinygamm4/ for the app. See https://youtu.be/SHqaZXSLaMw for a related youtube tutorial.

5. Simulation Studies

We conducted a series of simulation studies to verify the theoretical results and to examine the operating characteristics of the proposed tests, in comparison with the other L₂-based methods. We additionally investigated the influences of the number of knots on the tests.

5.1. Curve comparisons

For curve comparisons, we considered the following model

$$Y_{ij}=g_{id}\left(x_{ij}\right)+{ϵ}_{ij},$$ (9)

where i = 1, 2;j = 1, … , n_i.

In this simulation, we generated values of the independent variable x_ij from Unif[0, 1], with sample sizes n₁ and n₂ for the two comparison groups. The nonlinear functions for the two groups were specified as g₁(x) = 2xexp(2−4x)−2x+0.5 and g₂(x) = 2xexp(2−4x)−0.5, with g(x) = (4xexp(2−4x)−2x)/2. More generally, we considered g_id(x_ij) = (d/10)g_i(x_ij) + (1 − d/10)g(x_ij), with d = 0, 1, 2, 3, where d controlled the distance between the two group-specific functions. For example, d = 0 corresponded to the situation where the two groups shared the same regression function; as d increased, the functions grew further apart. These functions were plotted in Appendix B; see Supplemental Figure 1.

Values of the dependent variables Y_ij were generated from Equation (9) with standard errors σ₁ and σ₂, i.e.${ϵ}_{1j}~N\left(0,{\sigma }_1^2\right)$, ${ϵ}_{2j}~N\left(0,{\sigma }_2^2\right)$. Comparisons of the nonlinear functions were carried out under the following three conditions: (1) a distance parameter d = 0, 1, 2, 3; (2) sample sizes (n₁, n₂)=(125, 125), (216, 216), and (512, 512); (3) values of the error standard deviations (σ₁, σ₂)=(0.20, 0.15) and (0.25, 0.20).

With the generated data sets, we comparatively evaluated the performance of five discussed methods:

• Method 1: The proposed testing method with cubic B-spline regression bases for curve estimation, and a wild bootstrap procedure for p-value calculation.

• Method 2: The proposed testing method with penalized cubic spline bases for curve estimation, with a wild bootstrap procedure for p-value calculation by using the gam function in the R package mgcv. Numbers of knots were set to the default value, which was determined by a generalized cross-validation (GCV) method.

• Method 3: Kernel smoothing based on the L₂ distance test statistic, followed by a wild bootstrap procedure [19].

• Method 4: The testing method based on variance estimator [19].

• Method 5: Young and Bowman’s (1995) method [16], which calculates the p value by matching with a scaled chi-square distribution.

For each simulation setting, we generated a total of 1,000 testing datasets. For each dataset, we performed the proposed test on 200 wild bootstrap samples to calculate the p value. We calculated the rate of rejection in the 1,000 simulated samples at a significance level of 0.05.

Rejection rates for curve comparison under the null and alternative hypotheses are reported in Appendix B; see supplemental Table 1. When d = 0, the rejection rates are Type I error rates; when d = 1, 2, 3, the rejection rates represent the power of the tests. In comparison with other testing methods, the proposed tests in general had an excellent control of Type I error rates. As d increased, the power of rejecting the null hypothesis increased as well. The power of the new tests was comparable to, if not slightly better than, that of the existing tests. We noticed that Method 5 showed a slightly higher type I error rates than others. On the other hand, the Method 4 exhibited a tighter type I error control, while having considerably lower power. For the proposed testing methods, B-splines and penalized splines produced similar results. As previously discussed, we set the number of knots to $\sqrt[3]{n_1}$. In the simulation studies we observed that when an unpenalized semiparametric model was used, incorrect number of knots selection could lead to substantial bias and hence inflated the Type I error rates. The penalized semiparametric regression estimates, however, were generally very robust.

To verify the consistency theory in Section 3, we further examined the rejection rates (i.e., power) of the test as the sample size increased, under a fixed alternative hypothesis. We showed that when the distance between the null and alternative hypotheses was set to d = 1, the power increased with the sample size. The power approached to 1 when n₁ = n₂ = 1000. See Figure 2 in Appendix B.

Besides of the five methods listed above, we also compared the proposed methods with the test proposed by Kulasekera (1995) [13]. The latter’s performance has left much to be desired: In the tested settings, the type I error rates were close to zero, and the power was low as well. The suboptimal performance could be due to the simulation settings we chose, where the functional curves were close and data variability was large. The proposed tests, on the other hand, performed well in such situations. We omitted the results of Kulasekera’s test from the summary table.

We further examined the performance of the tests in situations of three group comparison. The nonlinear functions of the three groups were specified respectively as g₁(x) = 2xexp(2−4x)−x−(d₁/10)(x−0.5), g₂(x) = 2xexp(2−4x) − x + (d₂/10)(x − 0.5) and g₃(x) = 2xexp(2 − 4x) − x, with d_i = 0, 1, 2, 3 and i = 1, 2, where d₁, d₂ respectively controlled the distances between g₁ and g₃, and g₂ and g₃. Comparisons of the nonlinear functions were carried out with various distance values of d₁ and d₂, as well as sample sizes. For each setting, we generated a total of 500 testing datasets.

See Supplemental Table 2 in Appendix B for rates of rejection in 500 simulated samples at a significance level of 0.05. Similar to two curve comparisons, when d₁ = d₂ = 0, the proposed tests in general had a good control of type I error rates. As d_i increased, regardless the equal or unequal distances between the curves, the power of rejecting the null hypothesis increased with the sample size.

5.2. Surface comparisons

Simulations for surface comparisons were carried out in a similar manner. We used the following surface functions in the simulation:

1. g₁(x) = g₂(x) = sin(2πx₁) + cos(2πx₂)

2. $g_1\left(\mathbf{x}\right)=g_2\left(\mathbf{x}\right)=2x_1^2+3x_2^2$

3. $g_1\left(x\right)=g_2\left(x\right)=\text{exp}\left(-x_1^2-x_2^2\right)$

4. g₁(x) = sin(2πx₁) + cos(2πx₂) g₂(x) = sin(2πx₁) + cos(2πx₂) + x₁

5. $g_1\left(\mathbf{x}\right)=2x_1^2+3x_2^2{g}_2\left(\mathbf{x}\right)=2x_1^2+3x_2^2+\text{sin}\left(2\pi x_1\right)$

6. $g_1\left(\mathbf{x}\right)=\text{exp}\left(-x_1^2-x_2^2\right)g_2\left(\mathbf{x}\right)=\text{exp}\left(-x_1^2-x_2^2\right)+\text{sin}\left(2\pi x_1\right)$

Scenarios a-c represented situations under the null hypothesis, i.e., where the surfaces were the same; Scenarios d-f corresponded to various alternative hypotheses. The independent variables x₁ and x₂ were simulated from independent Unif[0, 1] with sample size n₁ and n₂ for each group. The dependent variables Y_ij were generated from the above functions with standard errors σ₁ and σ₂. i.e. Y_ij = g_i(x_ij) + ϵ_ij, where i = 1, 2; j = 1, … , n_i, ${ϵ}_{1j}~N\left(0,{\sigma }_1^2\right)$, ${ϵ}_{2j}~N\left(0,{\sigma }_2^2\right)$.

We conducted the simulation under the following parameter settings: (1) Three sample size settings of (n₁, n₂) as (125, 125), and (216, 216), (512,512); (2) Two different values of standard errors (σ₁, σ₂) for each function. For each simulation setting, we generated 500 datasets. For each dataset, we tested the new method with 300 wild bootstrap resamples. We calculated the rejection rate based on the 500 simulated datasets at α = 0.05.

Type I error rates for function pairs of a-c are reported in Appendix B; see supplemental Table 4; powers for function pairs in d-f are reported in Table 5 of Appendix B. The Type I error rates of the proposed tests were generally good and power was superior than the existing tests. Similar to the simulation studies for curve comparisons, the penalized semiparametirc model with the default number of knots from ‘GCV’ method showed a performance similar to the tests using semiparametirc estimating methods and $\sqrt[3]{n_i}$ number of knots. Numbers of knots had relatively minor influences on the testing performance.

In comparison with the existing methods, we found that in general the proposed methods had reasonable Type I error control as expected. The power was either comparable to or superior than that of the other methods.

5.3. Tests with correlated data

We considered the following models for correlated data

$$Y_{ijk}=g_{id}\left(x_{ijk}\right)+b_{ij}+{ϵ}_{ijk},$$

where i = 1, 2; j = 1, … , n_i; k = 1, 2, 3. As previously presented in Equation (9), we used Y_ijk to indicate the measure on the kth occasion in subject j from group i. Values of the independent variable x_ijk were generated from independent Unif[0, 1]. Values of the dependent variable Y_ij were generated based on the above functions with random effect $b_i~N\left(0,{\sigma }_i^{\prime }\right)$ and the i.i.d. random error ϵ_ijk ~ N(0, σ_i). We used the same regression functions in Section 5.1, where the two curves gradually grew apart with an increasing d (see Appendix Figure 1).

We considered the following parameter settings: (1) d=0, 1, 2; (2) three sample size settings (n₁, n₂) = (50, 60), (100, 120), and (150, 160) and all with three repeated measures; (3) three different combinations of the standard deviations of the random intercept and the i.i.d random variable as $\left({\sigma }_1^{\prime },{\sigma }_2^{\prime },{\sigma }_1,{\sigma }_2\right)=(0.2,0.15,0.04,0.05)$, (0.2, 0.15, 0.10, 0.12), and (0.25, 0.20, 0.10, 0.12). We used penalized semiparametric mixed regression to estimate the curves.

The simulation results are reported in supplemental Table 6 of Appendix B. Results suggested a relatively tight Type 1 error rate control and good power. Zhang’s (2000) scaled chi-square test is the only existing comparative test for correlated data [24]. We compared the performance of the new test with that of the scaled chi-square test. Under sample sizes (n₁, n₂) = (50, 50) and (100, 100), we performed the test using 1) the same x values for two groups; 2) slightly different x (x₂ = x₁ + Unif(0, 0.05)); 3) completely random and independent x₁, x₂ for two groups. Simulation was repeated for 200 times under each scenario and the results were shown in Appendix B Table 7.

The proposed test clearly outperformed the scaled χ² test. When the two groups had the same values in x, the scaled χ² test had Type I error rates that were lower than the nominal level. The power was generally lower as well. The scaled chi-square test was not designed for situations of randomly distributed independent variables so the power deteriorated when we introduced different x values between the two groups.

6. Real data applications

To illustrate the proposed testing procedures, we analyzed two data sets from a large observational study. The original study was designed to examine the factors related to blood pressure development in children. Detailed study protocols were published elsewhere [34][35]. Briefly, healthy children between 5 and 17 years of age were recruited from schools in Indianapolis, Indiana. Blood pressure, height, and weight were measured twice a year from the study participants. Blood and overnight urine samples were collected. The study protocol was approved by a local Internal Review Board. Informed consent was obtained from study participants, or their parents when appropriate.

6.1. Comparisons of weight growth curves

We compared the weight growth curves between blacks and whites within each sex, and between boys and girls within each race. We write the model as

$$\mathit{\text{Weigh}}{t}_{ij}=g_i\left(Ag{e}_{ij}\right)+{ϵ}_{ij},$$

where i indexes the groups and j the n_i observations within each group. Here we used the baseline assessment data to examine the weight-age relationships in the four sex and race combinations. The sizes of the four groups were: 205 black boys, 311 white boys, 232 black girls, and 289 white girls. We performed comparisons by testing the hypotheses H₀ : g₁ = g₂ vs H₁ : g₁ ≠ g₂, where g₁, g₂ are the weight growth curves between the sexes within each race group, or weight growth functions between the races within each sex group.

We first estimated the weight growth curves of the groups as part of the preliminary analysis. See scatter plots in Figure 1(a). We reported the p values of the four competing testing methods in Table 3. We presented the curve estimates with 95% pointwise confidence intervals from the semiparametric regression model (Generalized Cross-Validation for selecting smoothing parameter and thin-plate penalized basis function) in Figure 1(b). The nonparametric smoothing curves by loess produced curve estimates that were similar to the semiparametric regression estimates.

Figure 1:

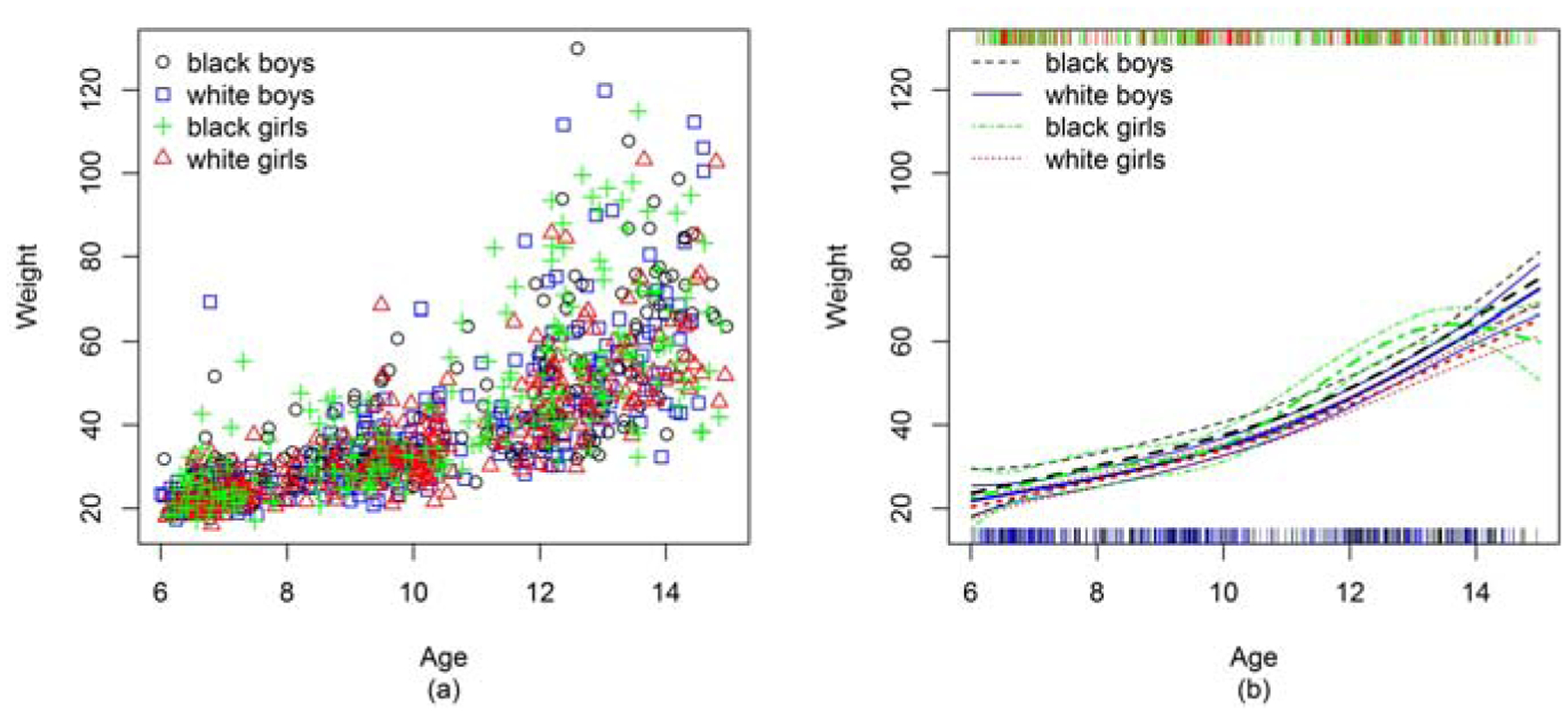
(a) Weight growth by race and sex; (b) Estimated weight growth curves with pointwise 95% CI, by race and sex

Testing results from the semiparametric spline-based estimating method were consistent with the curve estimations shown in Figure 1. The tests showed that the weight-for-age curves were significantly different between white and black girls. In our sample, the black girls gained more weight around ages 12 and 13 than their white peers, but the two curves converged gradually at age 14 years. The confidence intervals became wider after age 15, possibly due to the reduced sample sizes. Similar patterns were seen in the height-for-age curves.

For surface comparison, we considered weight as a function of age and height. We wrote the model as

$$\mathit{\text{Weigh}}{t}_{ij}=g_i\left(Ag{e}_{ij},\mathit{\text{Heigh}}{t}_{ij}\right)+{ϵ}_{ij},$$

where i is the index for the sex-race group, and j is the index for a specific subject, j = 1, 2, … , n_i within the group. We compared simultaneous effects of height and age on weight, among the four race-sex groups. The p-values of the four types of tests were summarized in Table 3 and the corresponding contour plots were presented in Figure 2 . No statistically significant differences were detected using the four tests.

Figure 2:

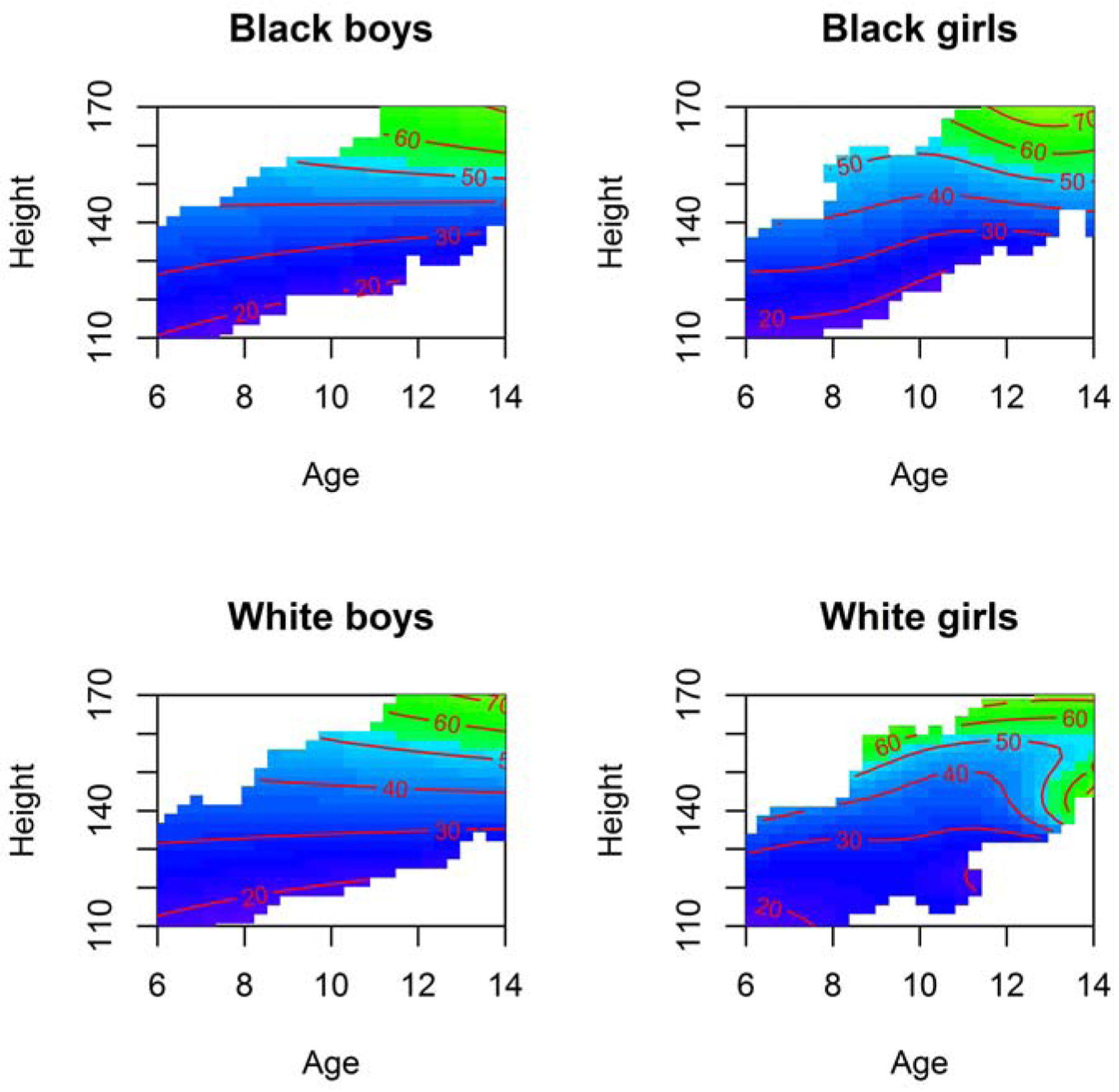
Estimated contour plots of weight as a function of height and age, by race and sex

6.2. Hormonal influences on blood pressure

Blood pressure is regulated by hormones in the renin-angiotensin-aldosterone system (RAAS). An essential product of RAAS is aldosterone, a mineralocorticoid hormone. Aldosterone acts on the epithelial sodium channel (ENaC) to help retain sodium. Increased sodium load causes extracellular fluid volume (ECFV) expansion, which in turn leads to blood pressure elevation. Recent biological experiments have shown that in the American population, blacks are more responsive to the stimulation of aldosterone in comparison to whites [35]. As a result, blacks tend to have greater levels of ECFV, which helps to suppress renin secretion. Renin, together with potassium, helps production of aldosterone [36]. This process is essential for the maintenance of blood pressure [37].

In this analysis, we examined the simultaneous influences of plasma renin activity (PRA) and plasma aldosterone concentration (PAC) on systolic blood pressure (BP):

$$B{P}_{ij}=g_i\left(log{\left(PRA\right)}_{ij},log{\left(PAC\right)}_{ij}\right)+{ϵ}_{ij},$$

where i is the index for the race group, and j is the index for a specific subject, j = 1, 2, … , n_i within the group. We were interested in comparing the surface functions in blacks and in whites. A quick visual examination (Figure 3) showed that blood pressure in whites (n=313) was on average lower than that in blacks (n=184). In whites, PRA and PAC were not significantly correlated with blood pressure, as one would expect in a steady-state sample. But in blacks, lower PRA and higher PAC were associated with a higher systolic blood pressure, which suggested an increased blood pressure sensitivity to aldosterone. We compared the two surface functions and obtained a p-value of 0.054, based on 500 bootstrap resamples. The comparison generated a p value that was close to, but did not reach the commonly accepted threshold of 0.05. Other testing methods, including Young and Bowman’s (1995) tests (Method 4 and 5 in Section 5.1) gave p-values of 0.15 and 0.73, while the L₂ distance-based test using kernel smoothing (Method 3 in Section 5.1) provided a p-value of 0.03. Indication for the racial difference in this analysis is generally consistent with the experimental evidence from drug-induced hyperaldosteronism in human subjects [35]; the actual power of the tests, however, is likely influenced by the sample size and data variability.

Figure 3:

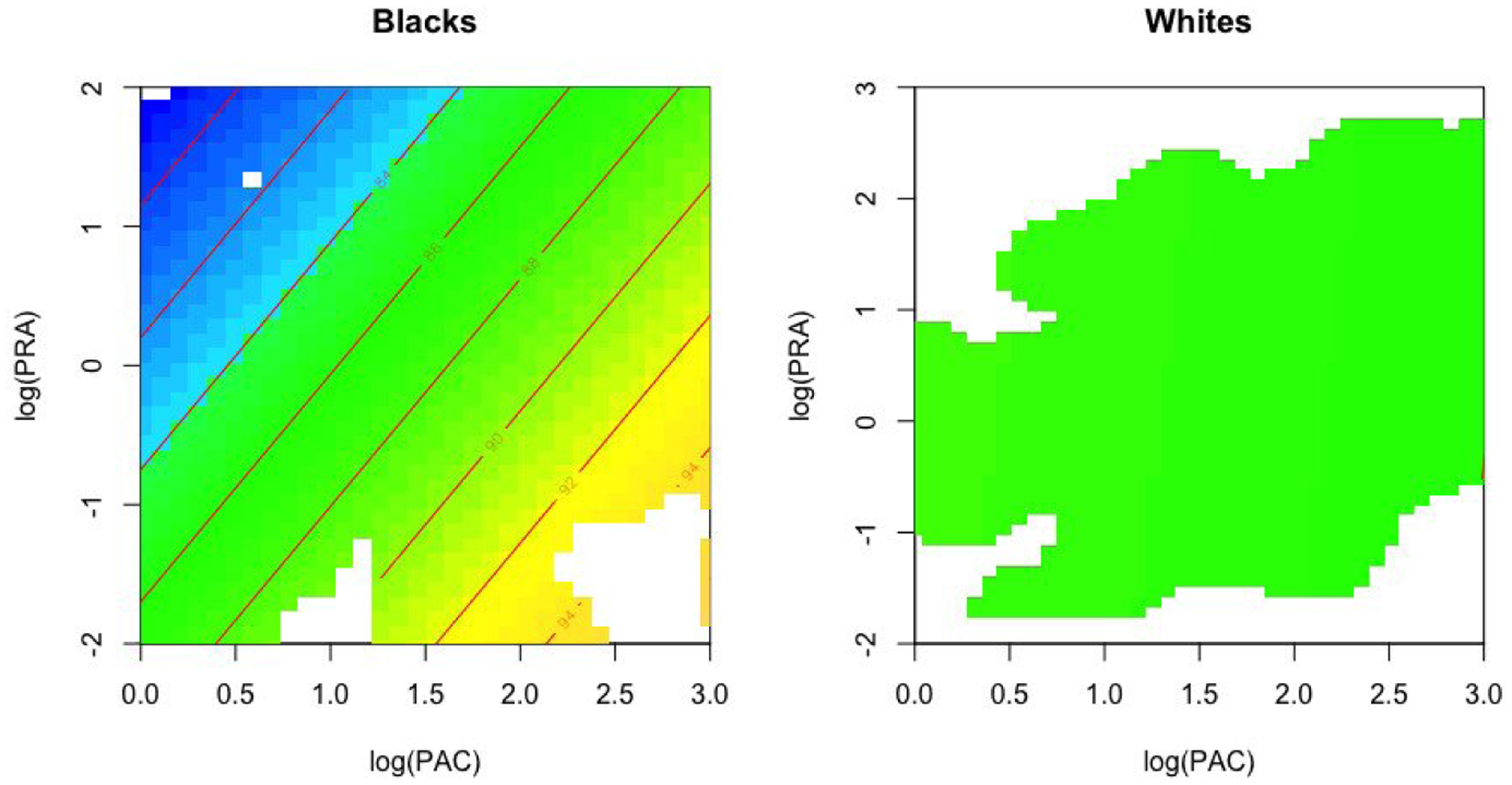
Estimated contour plots of systolic blood pressure as a function of logarithmic transformed plasma renin activity (PRA) and plasma aldosterone concentration (PAC), by race

7. Discussion

Statistical analysis of biomedical data is never complete without a proper test. In analysis of lower-dimensional nonlinear functions, inference typically involves comparisons of curves and surfaces. In parametric analysis where the functions are fully specified, inference is generally straightforward and can be carried out in the usual likelihood-based framework. In nonparametric or semiparametric analyses, due to lack of knowledge of the true functional forms of the relationships, hypotheses cannot be formulated solely on prespecified parameters. Analysts, therefore, can no longer rely on likelihood-based tests. Standard software packages or functions typically do not produce comparison of interest. In practice, estimation and inference of the functional curves and surfaces are often done separately, in part due to the lack of integration of estimation and inference tools and common programming syntax. In the present paper, we propose new testing procedures based on the L₂ distance. We show that the proposed tests are consistent against any fixed alternative hypothesis. To evaluate the level of statistical significance we provide a set of bootstrap testing methods. We have developed an R package to assist analysts who are interested in using the tests. For those who do not use R, we present an R Shiny interface to wrap around the software package so that analysts could directly upload their data to a web server and implement the tests through interactive web-based operations.

Extensive simulation studies show that, in comparison to the existing methods, the proposed tests have good control of type I error rate and excellent power. Despite our use of computer intensive methods such as the wild bootstrap, the procedures are generally quite efficient. Our own testing of the method with real data shows that the software package is easy to operate and it is flexible for accommodating covariates and repeated measures. We showed that the testing procedure possesses the property of consistency, a necessary condition for bootstrap to work. The rate of convergence, however, has not reached the optimum of n^1/2. The empirical evidence from our simulation has nonetheless supported the good performance in finite sample situations. Notwithstanding this limitation, we put forward a computational tool for the comparison of curves and surfaces in nonparametric or semiparametric analyses.