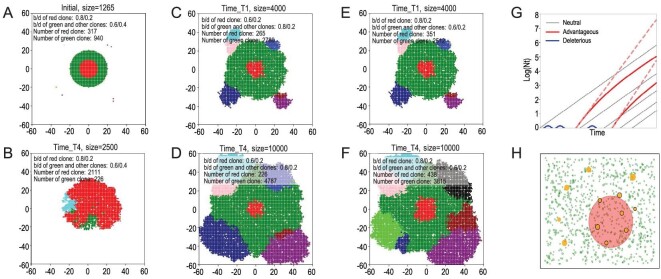
Figure 1.

The growth dynamics of competing tumors and the possibility of ‘tumors-in-tumor’. (A) The initial state of Rows 2 and 3. Different colors designate independently-emerged cell clones (ICCs) of a small area. The green clone is surrounded by a main clone colored in red with other clones scattered nearby. The red clone differs from the green and other clones in birth and death rate. (B) If the inside red clone has a selective advantage above a threshold, it would break out by engulfing and then eliminating the weaker green clone outside. (C and D) The clonal states at different time points when the total cell number is 4000 or 10 000. The red clone inside (birth rate at 0.6) is less fit than the green clone on the outside (birth rate at 0.8) with the death rate at 0.2 for both. (E and F) These two panels, the mirror images of (C) and (D), show the stronger red clone inside. It is most interesting to contrast the two rows of (C) and (D) vs. (E) and (F) that have remarkably similar dynamics despite the reversal in the selective advantage. This is because the selective coefficient (either positive or negative) is diluted to N^(1/3) of the initial value. (G) Tumor mass in log scale (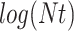 is linear if the clones grow exponentially (black lines). Red lines indicate advantageous clones that are much rarer than the neutral ones initially. Dotted red lines indicate exponential growth in a spatially panmictic population as in leukemia. In solid tumors, after the initial rapid growth, the fitness advantage gradually diminishes and approaches the rate of the neutral clones (solid red lines; see the text). The blue lines indicate clones less fit than the neutral ones, which would eventually disappear. (H) This panel illustrates another aspect of clonal competition when tumors are abutting each other without one being enclosed by the other. Hence, the clones grow more or less independently and the lesser ones are not eliminated. This coexistence may explain the dynamics of multifocal tumors in the literature.