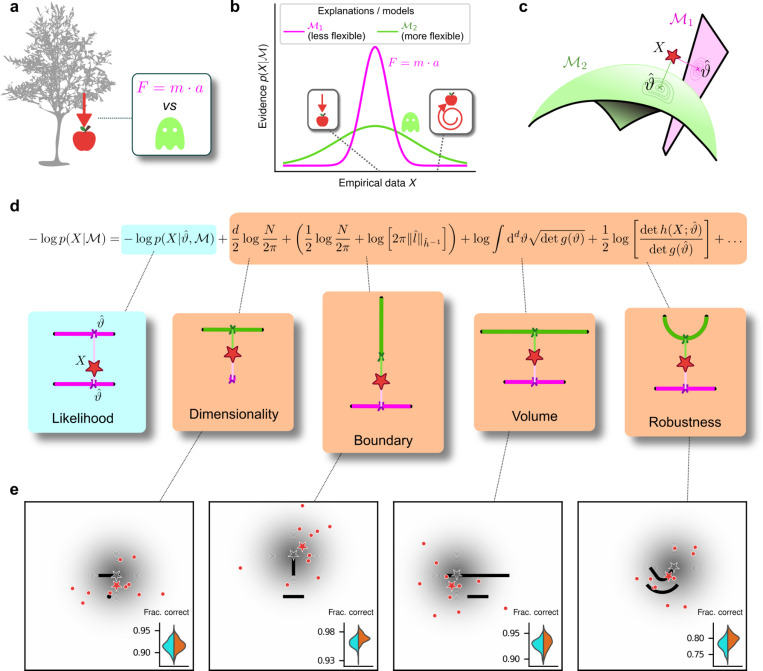
Figure 1: Formalizing Occam’s razor as Bayesian model selection to understand simplicity preferences in human decision-making.

a: Occam’s razor prescribes an aversion to complex explanations (models). In Bayesian model selection, model complexity quantifies the flexibility of a model, or its capacity to account for a broad range of empirical observations. In this example, we observe an apple falling from a tree (left) and compare two possible explanations: 1) classical mechanics, and 2) the intervention of a ghost. b: Schematic comparison of the evidence of the two models in a. Classical mechanics (pink) explains a narrower range of observations than the ghost (green), which is a valid explanation for essentially any conceivable phenomenon (e.g., both a falling and spinning-upward trajectory, as in the insets). Absent further evidence and given equal prior probabilities, Occam’s razor posits that the simpler model (classical mechanics) is preferred, because its hypothesis space is more concentrated around the sparse, noisy data and thus avoids “overfitting” to noise c: A geometrical view of the model-selection problem. Two alternative models are represented as geometrical manifolds, and the maximum-likelihood point $\widehat{\text{ϑ}}$ for each model is represented as the projection of the data (red star) onto the manifolds. d: Systematic expansion of the log evidence of a model $M$ (see previous work by Balasubramanian¹ and Methods section M.2). $\widehat{\text{ϑ}}$ is the maximum-likelihood point on model $M$ for data $X,N$ is the number of observations, $d$ is the number of parameters of the model, $\hat{l}$ is the likelihood gradient evaluated at $\widehat{\text{ϑ}},h$ is the observed Fisher information matrix, and $g$ is the expected Fisher information matrix (see Methods). $g(\text{ϑ})$ captures how distinguishable elements of $M$ are in the neighborhood of $\text{ϑ}$ (see Methods section M.2 and previous work¹). When $M$ is the true source of the data $X,h(X;\text{ϑ})$ can be seen as a noisy version of $g(\text{ϑ})$, estimated from limited data¹$.{\hat{h}}^{-1}$ is a shorthand for $h(X;\widehat{\text{ϑ}}{)}^{-1}$, and $\Vert \hat{l}{\Vert }_{{\hat{h}}^{-1}}=\sqrt{{\hat{l}}^T({\hat{h}}^{-1})\hat{l}}$ is the length of $\hat{l}$ measured in the metric defined by ${\widehat{h}}^{-1}$. The ellipsis collects terms that decrease as $N$ grows. Each term of the expansion represents a distinct geometrical feature of the model¹: dimensionality penalizes models with many parameters; boundary (a novel contribution of this work) penalizes models for which $\widehat{\text{ϑ}}$ is on the boundary; volume counts the number of distinguishable probability distributions contained in M; and robustness captures the shape (curvature) of M near $\widehat{\text{ϑ}}$ (see Methods section M.2 and previous work¹). e: Psychophysical task with variants designed to probe each geometrical feature in d. For each trial, a random location on one model was selected (gray star), and data (red dots) were sampled from a Gaussian centered around that point (gray shading). The red star represents the empirical centroid of the data, by analogy with c. The maximum-likelihood point can be found by projecting the empirical centroid onto one of the models. Participants saw the models (black lines) and data (red dots) only and were required to choose which model was best for the data. Insets: task performance for the given task variant, for a set of 100 simulated ideal Bayesian observers (orange) versus a set of 100 simulated maximum-likelihood observers (i.e., choosing based only on whichever model was the closest to the empirical centroid of the data on a given trial; cyan).