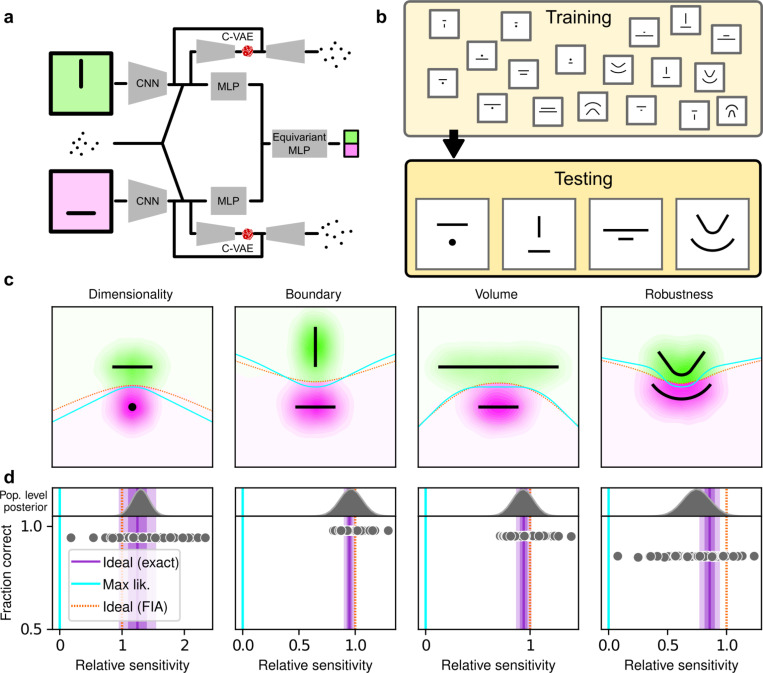
Figure 4: Artificial neural networks exhibit theoretically grounded simplicity preferences.

a: A novel deep neural-network architecture for statistical model selection. The network (see text and Methods for details) takes two images as input, each representing a model, and a set of 2D coordinates, each representing a datapoint. The output is a softmax-encoded choice between the two models. b: Each network was trained on multiple variants of the task, including systematically varied model length or curvature, then tested using the same configurations as for the human studies. c: Summary of network behavior, like Figure 2a. Hue (pink/green): k-nearest-neighbor interpolation of the model choice, as a function of the empirical centroid of the data. Color gradient (light/dark): marginal density of empirical data centroids for the given model pair, showing the region of space where data were more likely to fall. Cyan solid line: decision boundary for an observer that always chooses the model with highest maximum likelihood. Orange dashed line: decision boundary for an ideal Bayesian observer. d: Estimated relative sensitivity to geometrical features characterizing model complexity. As for the human participants, each fitted FIA coefficient was normalized to the likelihood coefficient and thus can be interpreted as a relative sensitivity to the associated FIA term. For each term, an ideal Bayesian observer would have a relative sensitivity of one (dashed orange lines), whereas an observer that relied on only maximum-likelihood estimation (i.e., choosing “up” or “down” based on only the model that was the closest to the data) would have a relative sensitivity of zero (solid cyan lines). Top: population-level estimate (posterior distribution of population-level relative sensitivity given the experimental observations; see Methods section M.6 for details). Bottom: each gray dot represents the task accuracy of one of 50 trained networks (y axis) versus the posterior mean estimate of the relative sensitivity for that network (x axis). Intuitively, the population-level posterior can be interpreted as an estimate of the location of the center of the cloud of dots representing individual subjects in the panel below. See Methods section M.6 for further details on statistical inference and the relationship between population-level and participant-level estimates. Purple: relative sensitivity of an ideal observer that samples from the exact Bayesian posterior (not the approximated one provided by the FIA). Shading: posterior mean ± 1 or 2 stdev., estimated by simulating 50 such observers.