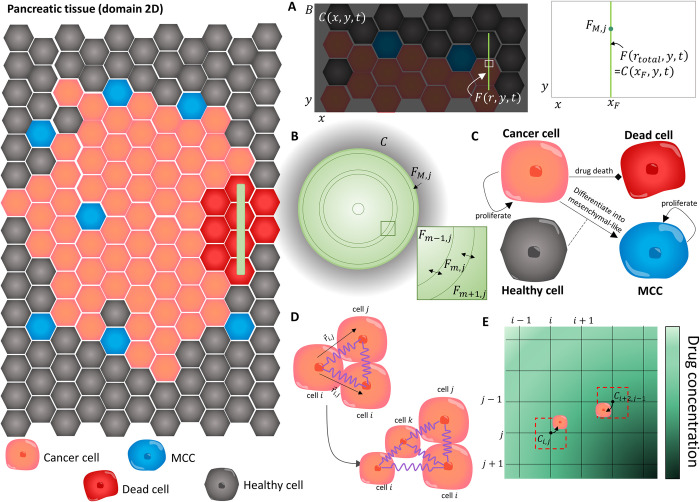
Fig 2. The main components of the VCBM–PDE model.

In the VCBM, we model the interactions between healthy cells (grey), cancer cells (orange), MCC (blue) and dead cells (read) in a 2–dimensional tumour microenvironment cross section. (A) The concentration of drug in the TME was modelled in a 2 dimensional domain bounded by B, where C(x,y,t) was the concentration in the TME at position (x,y). The fibre implant was then placed at a position x = x_F and modelled as a line source. To capture the diffusion of drug from the fibre, we modelled the concentration of gemcitabine inside the fibre F(r,y,t) at radial position r and domain position y where the continuity condition in Eq (3) required equal concentrations at the fibre boundary and at the immedicate local microenvironment, i.e. F(r_total,y,t) = C(x_F,y,t). (B) The concentration of gemcitabine inside the polymeric fibres was modelled by radially symmetric diffusion Eq (2) using a finite volume method (FVM) discretisation and considering the 2D cylindrical cross section of the fibres which have length L and radius r_total. The fibre was discretised into concentric annuli F_m,j at annulus m and cross section j, (i = 0,1,…,M) and the concentration of drug in each annulus F_m,j was modelled by considering drug diffusion across the bounadaries (e.g. F_m−1,j and F_m+1,j flow into F_m,j and vice vera). The full discretisation is presented in S1 Technical Supplementary Information. (C) Modelling assumptions for the VCBM were that cancer cells (orange) proliferate and some are able to cause epithelial to mesenchymal transtion and become invasive. We model this transition by assuming cells differentiate into a mesenchymal cancer cell (MCC) with one daughter cell placed on a neighbouring healthy cell. These MCCs cause the break down of surrounding tissue (i.e. replace healthy neighbouring cells with their progeny). Cancer cells can then die through gemcitabine uptake from their local environment. For more details see Fig B in S1 Text. (D) Individual cells were modelled as cell centres connected by springs [57]. The proliferation of a cell introduced a new cell into the lattice network which caused the rearrangement of the cells in the lattice with movement governed by Hooke’s law. (E) To simulate the gemcitabine concentration in the TME, Eq (1), we introduced a FVM discretisation, where the gemcitabine concentration was defined at discrete volumes centered around points in the discretisation. Cells could take up drug from the nearest grid point to their centre, and this concentration was used to determine their likelihood of drug–induced cell–death.