Free-Breathing Myocardial T₁ Mapping using Inversion-Recovery Radial FLASH and Motion-Resolved Model-Based Reconstruction

Abstract

Purpose:

To develop a free-breathing myocardial T₁ mapping technique using inversion-recovery (IR) radial fast low-angle shot (FLASH) and calibrationless motion-resolved model-based reconstruction.

Methods:

Free-running (free-breathing, retrospective cardiac gating) IR radial FLASH is used for data acquisition at 3T. First, to reduce the waiting time between inversions, an analytical formula is derived that takes the incomplete T₁ recovery into account for an accurate T₁ calculation. Second, the respiratory motion signal is estimated from the k-space center of the contrast varying acquisition using an adapted singular spectrum analysis (SSA-FARY) technique. Third, a motion-resolved model-based reconstruction is used to estimate both parameter and coil sensitivity maps directly from the sorted k-space data. Thus, spatio-temporal total variation, in addition to the spatial sparsity constraints, can be directly applied to the parameter maps. Validations are performed on an experimental phantom, eleven human subjects, and a young landrace pig with myocardial infarction.

Results:

In comparison to an IR spin-echo reference, phantom results confirm good T₁ accuracy, when reducing the waiting time from five seconds to one second using the new correction. The motion-resolved model-based reconstruction further improves T₁ precision compared to the spatial regularization-only reconstruction. Aside from showing that a reliable respiratory motion signal can be estimated using modified SSA-FARY, in vivo studies demonstrate that dynamic myocardial T₁ maps can be obtained within two minutes with good precision and repeatability.

Conclusion:

Motion-resolved myocardial T₁ mapping during free-breathing with good accuracy, precision and repeatability can be achieved by combining inversion-recovery radial FLASH, self-gating and a calibrationless motion-resolved model-based reconstruction.

Introduction

Quantitative myocardial T₁ mapping is becoming ever more important in clinical cardiovascular magnetic resonance (CMR) imaging [1, 2]. For example, both native and post-contrast T₁ mapping can be used to assess diffuse myocardial fibrosis [3]. Commonly used T₁ mapping techniques are modified Look-Locker inversion recovery (MOLLI) [4], saturation recovery single-shot acquisition (SASHA) [5], and saturation pulse prepared heart rate independent inversion recovery (SAPPHIRE) [6]. These techniques normally utilize a breathhold to mitigate respiratory motion and use an external electrocardiogram (ECG) device to synchronize data acquisition to a certain cardiac phase (e.g., end-diastolic), reducing the influence of cardiac motion. Although widely used, the need of a breathhold time of around 11 to 17 heartbeats may cause discomfort for patients (such as heart failure patients) and limits the achievable spatial resolution. Substantial efforts were made to shorten the breathhold period by optimized sampling [7], or by using non-Cartesian acquisition for single-shot myocardial T₁ mapping [8–10] or by cardiac magnetic resonance fingerprinting (MRF) techniques for efficient multi-parameter mapping [11–14]. More recently, free-breathing strategies [15–19] were investigated. These approaches acquire data continuously without the need for breath-holding and extract motion (respiration and/or cardiac) signals from the measured data itself using self-gating techniques. Following motion-resolved image reconstruction and pixel-wise fitting/matching, cardiac T₁ maps can then be obtained for certain motion states.

Model-based reconstruction [20–22] is an alternative approach to quantitative MRI. These methods directly reconstruct parameter maps from k-space, substantially reducing the number of unknowns to the number of actual physical parameters by not first reconstructing contrast-weighted images. They also offer a flexible choice of temporal footprint for parameter quantification as no intermediate image reconstruction is needed. Furthermore, sparsity constraints can be applied directly to the parameter maps to improve precision [23–25]. Model-based approaches have been used to accelerate myocardial T₁ mapping at high spatial resolution [26, 27], but still require breath-holding.

Combining idea from all these strategies, we aim to develop a free-breathing myocardial T₁ mapping technique by combining a free-running inversion-prepared radial FLASH sequence, an adapted self-gating technique and a calibrationless motion-resolved model-based reconstruction. In particular, the techniques integrate three novel developments: First, instead of setting the delay long enough to allow for a full T₁ recovery (> 5 s), we have derived an analytical formula for accurate T₁ calculation even when T₁ recovery is incomplete, i.e., ≤ 3 s. Second, to allow for robust respiratory motion estimation, we propose to use an extended technique based on SSA-FARY [28] to extract the respiratory motion signal from the k-space center by eliminating the trajectory-dependent oscillations and inversion contrast in a preprocessing step. Third, after sorting raw data into a number of respiration and cardiac bins based on the estimated respiration signal and the recorded ECG signal, we estimate both parameter maps and coil sensitivity maps of the desired motion bins directly from k-space using a calibrationless motion-resolved model-based reconstruction. The latter is an extension of a previously developed model-based reconstruction [24, 27] to the motion-resolved case which enables the application of sparsity constraints along all motion dimensions, in addition to the spatial regularization, to further improve T₁ precision. Validation of the proposed method was performed on an experimental phantom, eleven healthy subjects and one landrace pig with infarcted myocardium.

Theory

Sequence Design and T₁ Estimation from Incomplete Recovery

The free-running T₁ mapping sequence (free-breathing, retrospective cardiac gating) is shown in Figure 1 (A). It consists of three repeated blocks: (1) non-selective inversion (2) continuous radial FLASH readout using a tiny golden-angle (≈ 23.63°) [29] with a 3-s duration (3) and a time delay (T₁ recovery) before the inversion in the next repetition. In previous studies using multiple inversions [30, 31], the delay time was set long enough to ensure full recovery of longitudinal magnetization so that T₁ can still be calculated using the conventional Look-Locker formula [32, 33]. However, a full recovery may need as long as 5 seconds for cardiac T₁ mapping, which prolongs the total acquisition time. In this work, we treat this delay as a period that encodes T₁ information in the data. We use an analytical formula based on T₁, T₁*, the steady-state signal M_ss, and the new start magnetization signal $M_0^{\prime }$ (i.e., in the case that the T₁ recovery is not complete:$M_0^{\prime }<M_0$, with M₀ the equilibrium magnetization):

$$M_0^{\prime }=\frac{R_1{M}_{ss}{R}_1^{*}\left(1-E_1\right)+E_1{M}_{ss}\left(1-E_1^{*}\right)}{1+E_1\cdot E_1^{*}}$$ (1)

where $E_1=e^{-R_1\cdot t_1}$, $E_1^{*}=e^{-R_1^{*}\cdot t_{1s}}$, R₁ = 1/T₁, $R_1^{*}=1/T_1^{*}$ and t₁, t_1s are the time periods for T₁ and T₁* relaxation, respectively. Thus, T₁ can be estimated even from partial T₁ recoveries after reconstruction of the parameter maps ${\left(M_{ss},M_0^{\prime },R_1^{*}\right)}^T$ according to Equation (1). Here, we adopt a bisection root-finding algorithm to solve Equation (1). A full derivation of the above equation can be found in Section I of the Supporting Information File.

Figure 1.

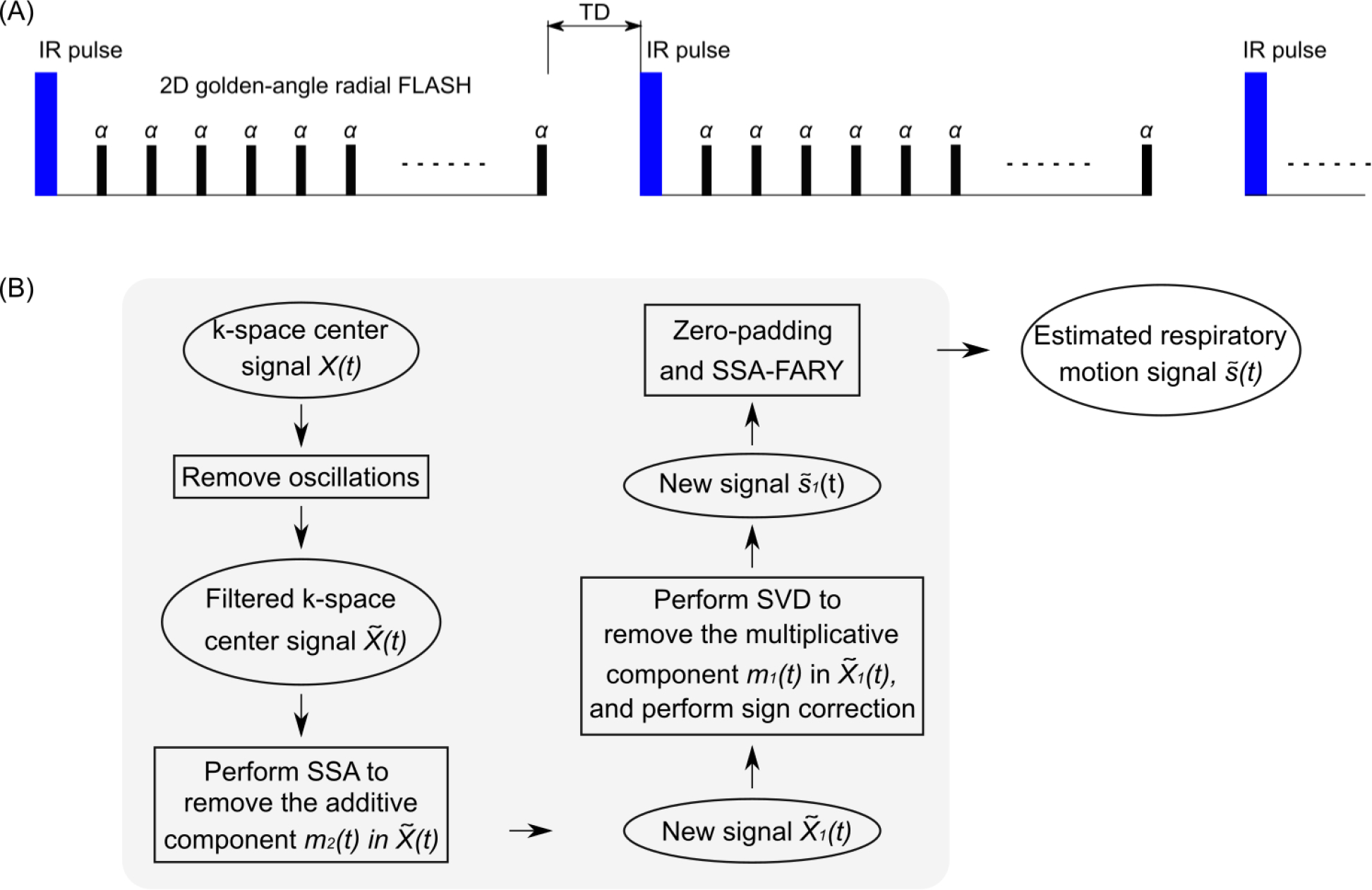
A. Schematic diagram of the free-running inversion-recovery radial FLASH sequence. Note TD is the delay time between inversions and this period encodes pure T₁ information in the data. B. Flowchart of the main steps in the adapted SSA-FARY technique for the respiratory motion signal estimation from the k-space center.

Respiratory Motion Estimation

The main steps of the respiratory motion estimation process are demonstrated in the flowchart in Figure 1 (B). In the following, we explain all these steps in detail. Similar to [28, 34], we construct an auto-calibration (AC) region for self-gating using the central k-space samples of a radial acquisition, resulting in a time-series X(t) of size [N_C × N_t], with N_C and N_t the total number of channels (phased array coils) and central k-space points, respectively. N_t = N_S · N_I, with N_S the number of sampling points per IR and N_I the total number of inversions. The AC data is usually corrupted by a trajectory-dependent signal due to eddy currents. Therefore, we first remove such oscillations by extending the method of orthogonal projections (with higher-order harmonics) from the steady-state case [28] to the contrast-change case (inversion recovery). Details of this procedure can be found in the Section II of the Supporting Information File.

Following removal of the oscillations, the new k-space center signal $\tilde{X}(t)$ can be modeled as

$$\tilde{X}(t)=s(t)\cdot m_1(t)+m_2(t)$$ (2)

with s(t) the steady-state signal which contains motion information (ideally without contrast change), and m₁(t) and m₂(t) the multiplicative and additive signals which model the contrast change due to inversion [35]. Here we propose the following procedure to remove the main effects from the changing contrast and to extract the signal component that is most relevant for respiratory motion:

• Step 1. Estimating m₂(t): Perform the singular spectrum analysis (SSA) on $\tilde{X}(t)$, remove the components that are mostly related to the inversion-recovery contrast in the spectrum domain and transfer the processed signal back to the time domain. In SSA [28], this step largely removes the additive contrast-changing component of Equation (2), resulting in a new signal ${\tilde{X}}_1(t)=\tilde{X}(t)-{\tilde{m}}_2(t)$, with ${\tilde{m}}_2(t)$ the estimated additive contrast-changing signal.

• Step 2. Estimating m₁(t): Since the multiplicative component is mainly left in Equation (2), the singular value decomposition (SVD) is then performed on ${\tilde{X}}_1(t)$ and the corresponding rank-one approximation is taken, generating an estimate of the multiplicative component ${\tilde{m}}_1(t)$. Next, the magnitude of ${\tilde{m}}_1(t)$ was utilized for the calculation, leading to a new signal $\tilde{s}(t)=\frac{{\tilde{X}}_1(t)}{\left|{\tilde{m}}_1(t)\right|}$. Due to the 180° phase difference before and after zero-crossing caused by inversion, the phase of $\tilde{s}(t)$ before zero-crossing needs to be inverted. This was done by first detecting the minimum points of the absolute value of signal $\tilde{X}(t)$ (zero-crossing) for each coil and inversion and then correcting using:

  $${\tilde{s}}_1(t)=\{\begin{array}{ll}-\tilde{s}(t),\hfill & \text{if}t\le \text{zero-crossing}\hfill \\ \tilde{s}(t),\hfill & \text{otherwise}.\hfill \end{array}$$ (3)

• Step 3. Zero-padding: To account for the missing temporal information due to the delay time between inversions, ${\tilde{s}}_1(t)$ was zero-padded, generating a new signal ${\tilde{s}}_2(t)\in C^{\left[N_C\times \left(N_I\cdot \left(N_S+N_{\text{Z}}\right)\right)\right]}$ with N_Z calculated by $N_{\text{Z}}=\frac{\text{Delay}\text{Time}}{\text{Repetition}\text{Time}\left(\text{TR}\right)}$.

• Step 4. SSA-FARY: Perform SSA-FARY on ${\tilde{s}}_2(t)$ with the window size tuned to estimate the signal component that is most relevant for the respiratory motion.

Motion-Resolved Model-Based Reconstruction

The acquired k-space data is then sorted into 6 respiration and 20 cardiac bins using amplitude binning [36] based on the estimated respiratory signal and the recorded ECG signal. The MR physical parameter maps in Equation (1) for the selected motion states are estimated directly from k-space using a calibrationless model-based reconstruction [24, 27]. Here, to further exploit sparsity along the motion dimensions, the previous model-based reconstruction is extended to the motion-resolved case by formulating the estimation of unknowns from the selected motion states as a single regularized nonlinear inverse problem:

$$\widehat{x}=\underset{x\in S}{\arg \min }\sum _{r=1}^{T_R}\sum _{c=1}^{T_C}{\Vert F_{r,c}(x)-Y_{r,c}\Vert }_2^2+\alpha R\left(x_{\mathit{m}}\right)+\beta U\left(x_{\mathit{c}}\right)$$ (4)

where F is a nonlinear operator [27] mapping all unknowns x to the sorted k-space data Y. T_R, T_C are the numbers of respiration and cardiac bins, respectively. x = (x_m, x_c)^T where x_m contains MR physical parameter maps in Equation (1), i.e., ${\left(M_{ss},M_0^{\prime },R_1^{*}\right)}^T$ of all the selected motion states and x_c represents coil sensitivity maps ${\left(c_1,\cdots ,c_{N_C}\right)}^T$ for the corresponding motion states. S is a convex set ensuring non-negativity of the relaxation rate $R_1^{*}$. For the regularization R(·), we first adopt the joint ℓ₁-Wavelet spatial constraints [24]. Second, we add the temporal total variation (TV) regularization to explore sparsity along the motion dimensions [37]. Furthermore, as a pure TV may favor straight lines if applied along the motion dimension only, we utilize a joint TV regularization along spatial and temporal dimensions to better preserve the spatio-temporal information. Thus, R(·) reads:

$$R\left(x_{\mathit{m}}\right)={\lambda }_1{\Vert W{x}_{\mathit{m}}\Vert }_1+\sqrt{{\lambda }_2{\Vert D_x{x}_{\mathit{m}}\Vert }^2+{\lambda }_3{\Vert D_y{x}_{\mathit{m}}\Vert }^2+{\lambda }_4{\Vert D_c{x}_{\mathit{m}}\Vert }^2+{\lambda }_5{\Vert D_r{x}_{\mathit{m}}\Vert }^2}$$ (5)

with ${\Vert W{x}_{\mathit{m}}\Vert }_1$ the joint ℓ₁-Wavelet spatial regularization and D_x, D_y, D_c and D_r the gradient operators along the x, y, cardiac and respiratory dimensions, respectively. λ₁, λ₂, λ₃, λ₄ and λ₅ are the corresponding weighting parameters, balancing the effects of different regularization terms. α is a global regularization parameter on R(·). U(·) represents the Sobolev regularization term [38] on the coil sensitivity maps with β the regularization parameter. Similar to [24, 27], the above nonlinear inverse problem is solved by the iteratively regularized Gauss-Newton method (IRGNM) algorithm [39] where the nonlinear problem in Equation (4) is linearizedly solved in each Gauss-Newton step. To enable the use of multiple regularizations, the ADMM algorithm [40] was employed to solve the linearized subproblem. More details of the proposed IRGNM-ADMM algorithm can be found in Appendix I.

Methods

Data Acquisition

All MRI experiments were performed on a Magnetom Skyra 3T (Siemens Healthineers, Erlangen, Germany) with approval of the local ethics committee. Animal care and all experimental procedures were performed in strict accordance with the German and National Institutes of Health animal legislation guidelines and were approved by the local animal care and use committees. Validations were first performed on a commercial reference phantom (Diagnostic Sonar LTD, Scotland, UK) consisting of 6 compartments with defined T₁ values surrounded by water. Phantom scans employed a 20-channel head/neck coil, while in vivo measurements used combined thorax and spine coils with 26 channels. In the phantom study, the delay time TD in the sequence was varied from 5 s to 1 s (with a step size of 1 s) to study T₁ accuracy and precision when using the proposed T₁ estimation procedure. An optimal value of TD was then chosen for subsequent in vivo studies. Informed written consent was obtained from all subjects prior to MRI. In vivo scans were performed during free-breathing using the free-running sequence. The ECG signals were recorded for later use but not for triggering. To assess repeatability of the proposed method, the sequence was repeated twice in the middle short-axis slice for each subject. Data from basal and apical slices were additionally acquired for a subset of subjects. After excluding measurements with non-reliable ECG signal, data sets from eleven subjects (seven female, four male, age 25 ± 4, range 21 – 37 years; heart rates 63 ± 9 bpm, range 50 – 77 bpm) were used in this work (including six subjects with basal and apical slices). For FLASH readout, spoiling of the residual transverse magnetization was achieved using random radiofrequency (RF) phases [41]. The other acquisition parameters were: field of view (FOV) = 256 × 256 mm², slice thickness = 6 mm, matrix size = 256 × 256, TR/echo time (TE) = 3.27–3.30/1.98 ms, RF-pulse time-bandwidth product = 4.5, nominal flip angle = 6°, receiver bandwidth = 810 Hz/pixel and total acquisition time of 21 inversions, i.e., around 2 min with 915 radial spokes per inversion. A window size of 21 frames was chosen for the adapted SSA-FARY technique [28]. Further, one data set from a young landrace pig with infarcted myocardium (regions in the septum and anterior wall due to intermittent left anterior descending artery occlusion) was acquired on the mid-ventricular short-axis slice using the same free-running acquisition parameters described above.

For reference, gold standard T₁ mapping was performed on the phantom using an IR spin-echo method [42] with 9 IR scans (TI = 30, 530, 1030, 1530, 2030, 2530, 3030, 3530, 4030 ms), TR/TE = 4050/12 ms, FOV = 192 × 192 mm², slice thickness = 5 mm, matrix size = 192 × 192, and a total acquisition time of 2.4 h. For in vivo studies, a 5(3)3 MOLLI reference sequence with a hyperbolic tangent inversion pulse [43] provided by the vendor was applied for end-diastolic T₁ mapping using a FOV of 360 × 306.6 mm², in-plane resolution = 1.41 × 1.41 × 8 mm³, TR/TE = 2.7/1.12 ms, nominal flip angle = 35°, receiver bandwidth=1085 Hz/pixel and an acquisition period of 11 heart beats during a single breathhold. A correction factor was further applied to the final MOLLI T₁ map to accommodate for the imperfect inversion [43].

Iterative Reconstruction

The motion-resolved model-based reconstruction algorithm was implemented using the nonlinear operator and optimization framework in C/CUDA in the Berkeley Advanced Reconstruction Toolbox (BART) [44]. To reduce computational demand, we selected three respiratory motion bins (out of 6) close to the end-respiratory state and all cardiac bins for the motion-resolved quantitative reconstruction. Similar to [24], we initialized the parameter maps ${\left(M_{ss},M_0^{\prime },R_1^{*}\right)}^T$ with (1.0, 1.0, 1.5)^T and all coil sensitivities with zeros in the IRGNM-ADMM algorithm. Moreover, as a high accuracy is usually not necessary during the first Gauss-Newton steps, we set the number of ADMM iteration steps to be N_n = min(100, 2N_n−1) at the n-th Gauss-Newton step with N₀ = 10. This setting resulted in stable reconstructions for all cases tested.

Regularization parameters were tuned to balance the preservation of image details versus reduction of noise. The regularization parameters α and β were initialized with 1.0 and subsequently reduced by a factor of three in each Gauss-Newton step. A minimum value of α was used to control the noise of the estimated parameter maps even with a large number of Gauss-Newton steps, i.e., α_n+1 = max(α_min, (1/3)ⁿ · α₀). The optimal value α_min as well as the weighting parameters λs were chosen manually to optimize the signal-to-noise ratio (SNR) without compromising the quantitative accuracy or delineation of structural details. Particularly, α_min was tuned from 0.004 to 0.007 with the optimal value chosen by visual inspection. λ₁ was set to be 0.2 and parameters (λ₂, λ₃, λ₄, λ₅)^T in the weighted spatio-temporal TV regularization term in Equation (5) were set to be (0.4, 0.4, 1.0, 0.2)^T. For comparison, the other types of regularization, such as the spatial-only (ℓ₁-Wavelet) regularization (R(x_m) = λ₁∥Wx_m∥₁), temporal TV regularization (R(x_m) = λ₄∥D_cx_m∥₁ + λ₅∥D_rx_m∥₁) and the combination of the above two (R(x_m) = λ₁∥Wx_m∥₁ + λ₄∥D_cx_m∥₁ + λ₅∥D_rx_m∥₁) were also implemented and first evaluated on a simulated dynamic phantom using the parallel imaging and compressed sensing (PICS) tool in BART, followed by the evaluation on the data of one subject with the proposed motion-resolved model-based reconstruction. More details regarding the simulated dynamic phantom can be found in Section III of the Supporting Information File.

With the above parameter settings, all image reconstruction was done offline. After gradient-delay correction [45] and channel compression to six principal components, the multi-coil radial data were gridded onto a Cartesian grid, where all successive iterations were then performed using FFT-based convolutions with the point-spread function [46]. To reduce memory demand during iterations, 15 spokes were binned into one k-space frame prior to model-based reconstruction, resulting in a nominal temporal resolution of around 49 ms. To allow for efficient reconstructions, implementations were optimized in BART (see Section IV of the Supporting Information File) so that all computations could run on a GPU (A100, NVIDIA, Santa Clara, CA) with a memory of 80 GB. It then took around 20 – 30 minutes to reconstruct one in vivo data set using the above reconstruction parameters.

T₁ Analysis

All quantitative T₁ results are reported as mean ± standard deviation (SD). For the in vivo studies, T₁ maps from the end-diastolic and end-respiratory phase were selected for quantitative assessment of the proposed method. Regions-of-interest (ROIs) were carefully drawn into the myocardial segments model defined by the American Heart Association (AHA) [47] with 6 segments in the basal and middle slices and 4 segments in the apical slice using the arrayShow [48] tool in MATLAB (MathWorks, Natick, MA). The mean T₁ values were calculated for each segment across all subjects and scans, and were visualized with bullseye plots. The repeatability error was calculated using $\sqrt{\left({\sum }_{i=1}^{n_s}{T}_{1\text{diff}}^2(i)\right)/n_s}$, with T_1diff(i) the T₁ difference between two repeated measurements and n_s the number of subjects. The precision of T₁ estimation was computed using the coefficient of variation (CoV = SD_ROI / Mean_ROI × 100%). Further, Bland-Altman analyses were performed to compare ROI-based mean T₁ values between different T₁ mapping techniques. The two-tailed Student’s t-tests were utilized for comparison, and a p value < 0.05 was considered significant. In addition, to quantify the in-plane cardiac motion between end-diastolic and end-systolic phases, the relative difference of the left-ventricular area (Area_{End-Diastolic} − Area_End-Systolic / Area_{End-Diastolic} × 100%), similar to the left-ventricular ejection fraction (LVEF) index for the volume case, was calculated based on the mid-ventricular myocardial T₁ maps. The blood–myocardium boundary was manually segmented using the aforementioned arrayShow tool.

Results

Phantom Validation

We first validated the proposed T₁ correction procedure for phantom T₁ mapping when using different delay times in the multi-shot acquisition in comparison to an IR spin-echo reference. Figure 2 presents the estimated T₁ maps for acquisitions with delay times ranging from five seconds to one second (step size one second) when using the conventional Look-Locker formula and the proposed procedure. Prior to T₁ correction, all the physical parameters ${\left(M_{ss},M_0^{\prime },R_1^{*}\right)}^T$ were estimated by the single-slice model-based reconstruction [24] using the data from the second inversion, where the initial magnetization is affected by incomplete recovery. Both quantitative T₁ maps and T₁ values of a ROI in Figure 2 as well as the Bland-Altman plots in the Supporting Information Figure S1 (A) reveal that the conventional Look-Locker correction underestimates T₁: the smaller the delay time, the higher the bias. On the other hand, the proposed procedure could achieve good T₁ accuracy regardless of the delay time, but at the expense of increased noise (i.e., lower precision) for short delays and large T₁ times. This is mainly due to the fact that there is less T₁ information encoded in the data for shorter delays. In the extreme case where there is no delay, it is impossible to recover T₁ (i.e., decouple T₁ and $B_1^{+}$ from $T_1^{*}$) as no explicit T₁ is encoded in the data. According to these results, a delay time of two or three seconds is a good compromise between short acquisition time and good T₁ precision. We choose three seconds for the other acquisitions in this study.

Figure 2.

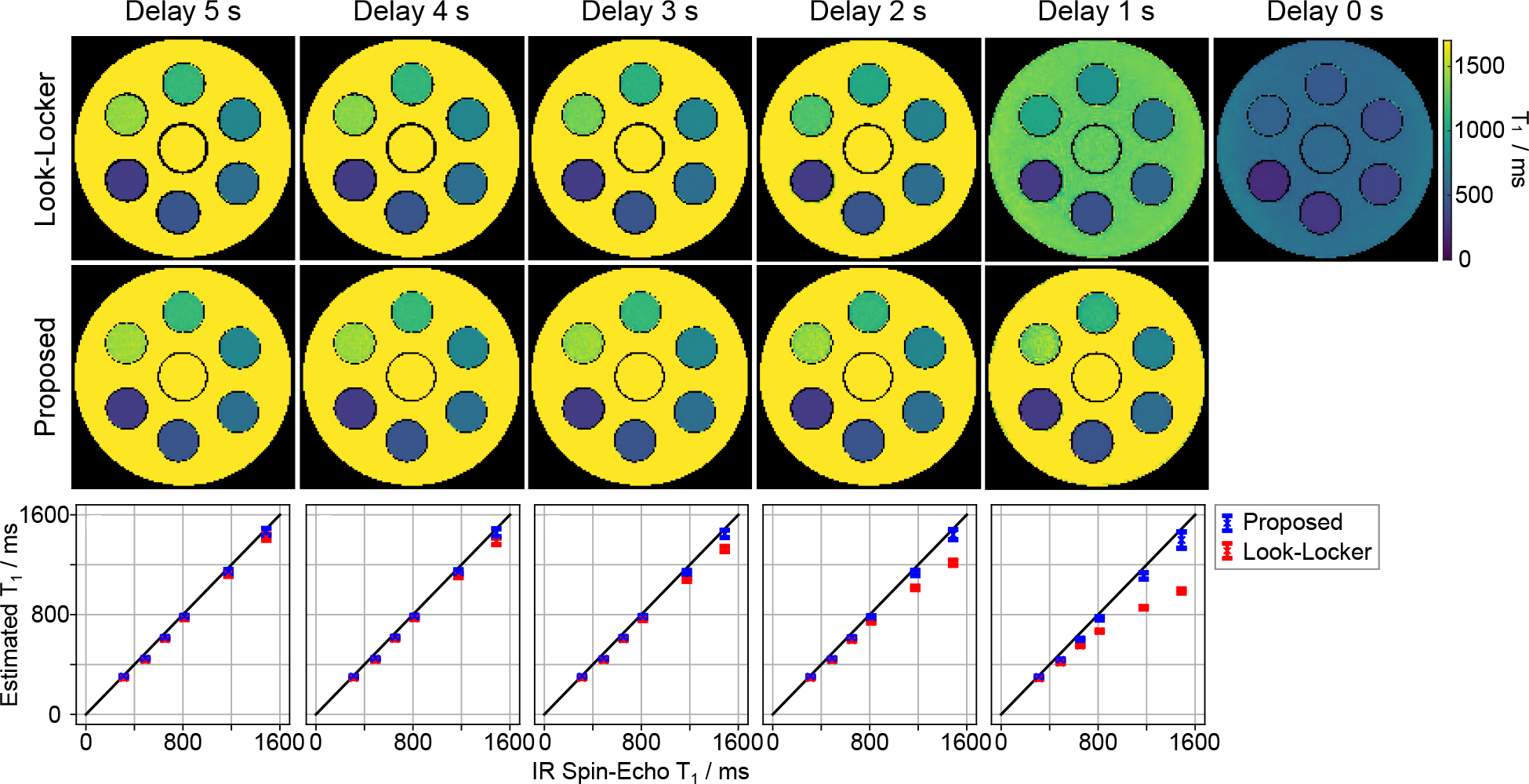
Quantitative phantom T₁ maps with various delay times from 5 s to 1 s (step size 1 s) using (top) the conventional Look-Locker correction and (middle) the proposed formula. (Bottom) Quantitative T₁ values (mean and standard deviation) within ROIs of the 6 phantom tubes in comparison to an IR spin-echo reference. The corresponding Bland-Altman plots are shown in the Supporting Information Figure S1 (A).

Subsequently, we evaluated the proposed motion-resolved model-based reconstruction on the same phantom using the multi-shot data with the delay time of three seconds. The data has been sorted into 6 respiratory and 20 cardiac motion states based on the motion signals estimated from one human subject (subject #3, scan #1). Figure 3 (top) shows the estimated phantom T₁ maps (selected at the end-expiration and end-diastolic phase) with the spatial-only regularization using two different regularization parameters α_min = 0.005 and α_min = 0.02, and its combination with the spatio-temporal TV regularization with α_min = 0.005. Figure 3 (bottom) plots the corresponding quantitative T₁ values of the ROI against the IR spin-echo reference. The Supporting Information Figure S1 (B) further presents the corresponding Bland-Altman plots. The above quantitative results show that all reconstructions could achieve good T₁ accuracy. The increase of the regularization strength in the spatial-only regularization or the use of an additional spatio-temporal TV with the same regularization parameter is helpful for reducing noise (improving T₁ precision) in the quantitative phantom T₁ maps.

Figure 3.

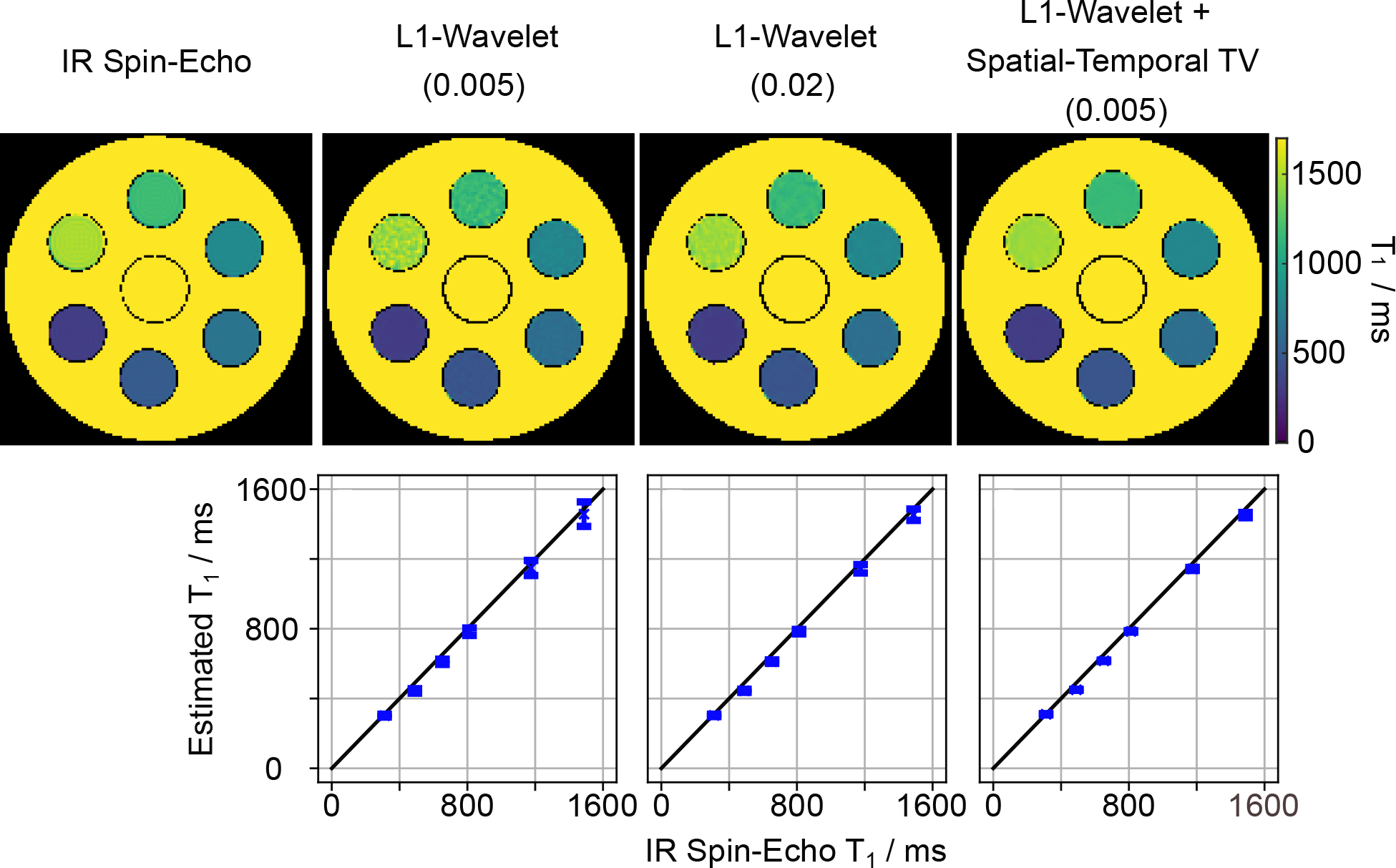
(Top) Phantom T₁ maps reconstructed with different regularization using the motion-resolved model-based reconstruction in comparison to an IR spin-echo reference. (Bottom) Quantitative T₁ values (mean and standard deviation) within ROIs of the 6 phantom tubes. The value in the bracket (top) indicates the regularization parameter α_min used for each reconstruction. The corresponding Bland-Altman plots are presented in the Supporting Information Figure S1 (B).

In Vivo Studies

Respiratory Motion Estimation

Figure 4 shows the DC component for one inversion recovery before and after data correction using the extended orthogonal projection with the order of harmonics N_H set to five. Some coils exhibit strong oscillations. The oscillation period in the AC data is linked to the period of the projection angle used in the radial acquisition [28]. By removing this frequency and the higher-order harmonics, these oscillations can be largely eliminated. The filtered DC component is then used for self-gating.

Figure 4.

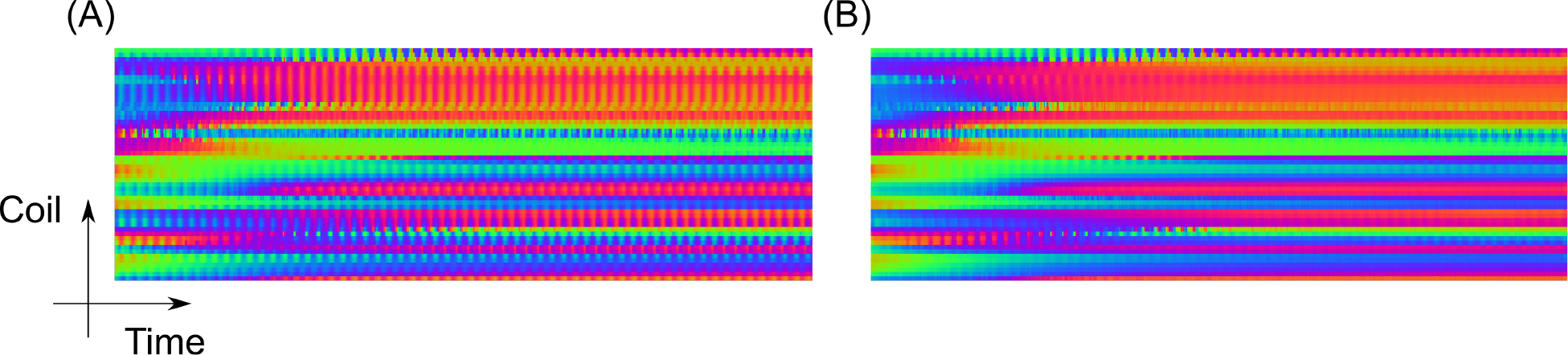
Snippet of the complex plot with color-coded phase of the DC samples used for auto-calibration before (A) and after (B) data correction with the extended orthogonal projection. Notably less disturbing oscillations are observed in B. The above snippet corresponds to one complete inversion recovery (3 s).

The background of Figure 5 (A) represents the temporal evolution of a line profile extracted from a real-time image reconstruction [46] of the free-running IR radial FLASH with 12 inversions. The line was placed in the vertical direction of the real-time image series where the diaphragmatic motion can be observed, as demonstrated by the white vertical line in Figure 5 (B). On top of the line profiles, the estimated respiratory signal and the signal provided by the respiratory belt are plotted. All motion signals have been scaled for better visual comparison. The estimated respiratory signal coincides well with the motion of the diaphragm in the real-time images. The adapted SSA-FARY technique could also provide reliable motion signal in the region where the respiratory belt failed to produce a signal (pointed out by a white arrow). Figure 4 (B) shows the corresponding steady-state images reconstructed with the non-uniform fast Fourier transform (nuFFT) after binning the data into 6 respiratory motion states using the estimated respiration signal. As indicated by the dashed lines, the different inspiration and expiration phases are well resolved. Figure 5 (C) and (D) show a similar comparison for the pig experiment where reliable respiratory signal can be obtained, suggesting robustness of the adapted SSA-FARY technique.

Figure 5.

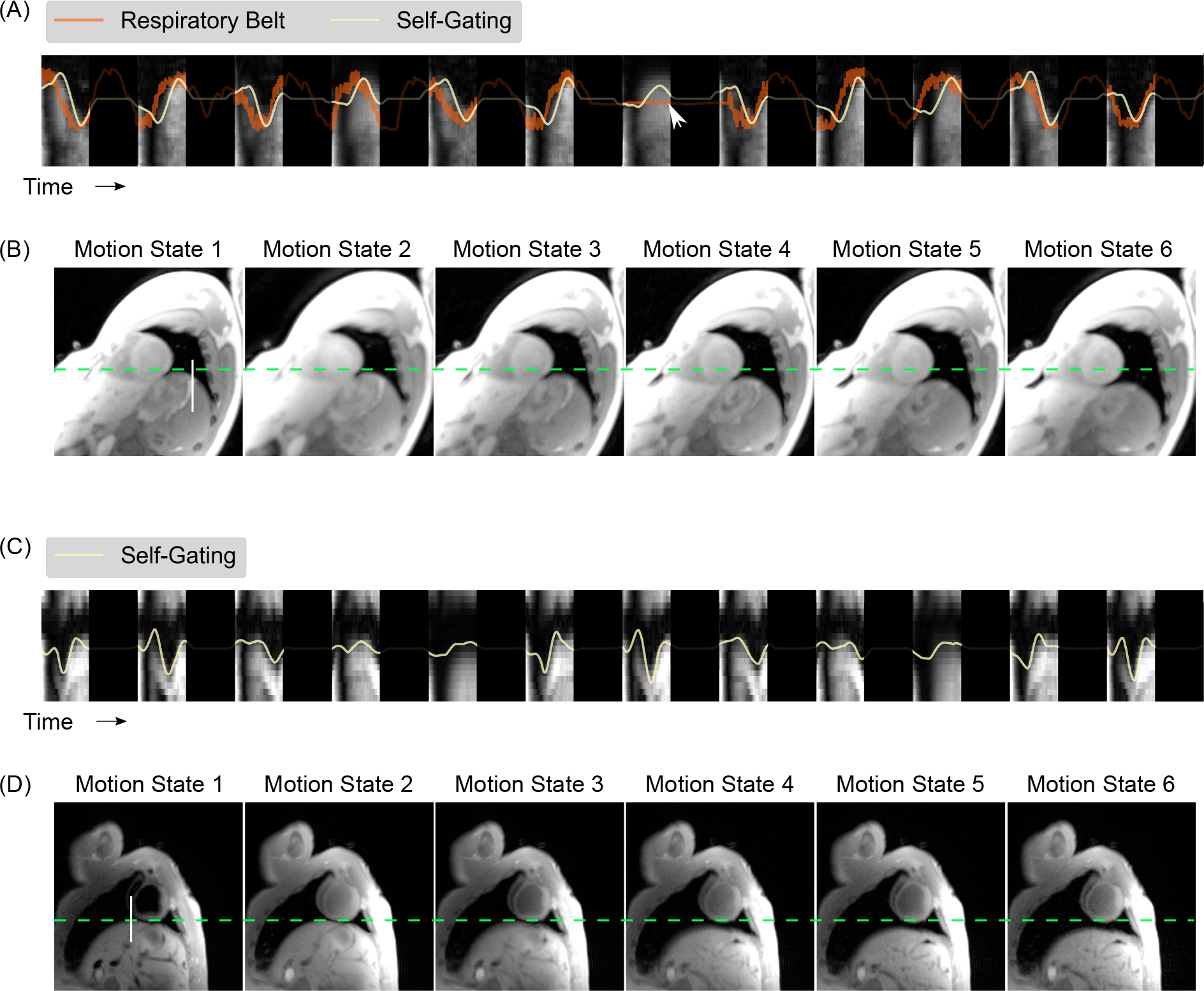
A. Comparison of the estimated respiratory signal with that obtained from the respiratory belt for 12 inversions for a healthy subject. The background image represents the temporal evolution of a vertical line profile (white line in B) extracted from a real-time image reconstruction [46] of the data acquired with free-running IR radial FLASH. The dark regions represent the time delay between inversions. The white arrow indicates a time point where the respiration belt failed to provide a signal. B. The corresponding steady-state images reconstructed by the non-uniform fast Fourier transform after binning the data (combing all cardiac phases) into 6 respiratory motion states. The dashed green line serves as a baseline for the end-respiration motion state. (C) and (D) show similar results for the pig experiment but with the respiratory belt signal absent.

Model-Based Myocardial T₁ Mapping

We validated the effects of different regularization types used in the model-based reconstruction. Figure 6 shows myocardial T₁ maps (at the selected end-expiration and end-diastolic phase) for one subject and the corresponding T₁ line profiles (as indicated by the dashed black line) through all cardiac phases with various regularization types. The regularization parameter α_min has been optimized for each type of reconstruction individually. In particular, α_min was set to be 0.02, 0.02, 0.006 and 0.005 for spatial (ℓ₁-Wavelet) only, temporal TV only, combined spatial (ℓ₁-Wavelet) and temporal TV, and the proposed regularization that combines spatial (ℓ₁-Wavelet) and a spatio-temporal TV, respectively. The spatial (ℓ₁-Wavelet) only regularization creates noisy and degraded myocardial T₁ maps. The temporal TV regularization could improve the image quality significantly by exploiting temporal sparsity. However, this kind of regularization also favors straight lines and thus creates “line”-like artifacts along the time/motion dimension (as seen the line profile images). The combination of spatial (ℓ₁-Wavelet) and temporal TV regularization could reduce these “line”-like effects as a weaker temporal TV regularization is sufficient to achieve a similar denoising effect. Finally, the spatio-temporal TV regularization that combined both spatial and temporal information in a single multi-dimensional TV regularization, and its combination with the spatial (ℓ₁-Wavelet) regularization, could achieve an even better compromise between denoising and the preservation of subtle motion in the line profiles (indicated by the black arrows) than the other types of regularization. Noteworthy, the myocardial T₁ map from the spatial-only regularization is noisier than our previous single-shot results [27]. This is mainly due to the fact that there is much less data in one motion state in the motion-resolved reconstruction than the one in [27] which combines data from several diastolic phases (e.g., ~285 spokes vs ~800 spokes). The Supporting Information Figure S2 shows a similar comparison of the effects of various regularization types on a simulated dynamic phantom with three small tubes on the “myocardium”, mimicking certain “lesions”. Here, all reconstructions were done with the same regularization parameter. In line with the in vivo results presented here, the spatial regularization-only reconstruction results in blurred images with artifacts and signal inhomogeneities on the “myocardium” due to high undersampling. Temporal TV regularization is able to largely remove the above artifacts and improve image sharpness by exploiting the temporal sparsity but favors “line”-like artifacts along the motion dimension. On the contrary, the proposed spatio-temporal TV combined with the spatial (ℓ₁-Wavelet) regularization has the best performance in denoising and preservation of both spatial and temporal structure details.

Figure 6.

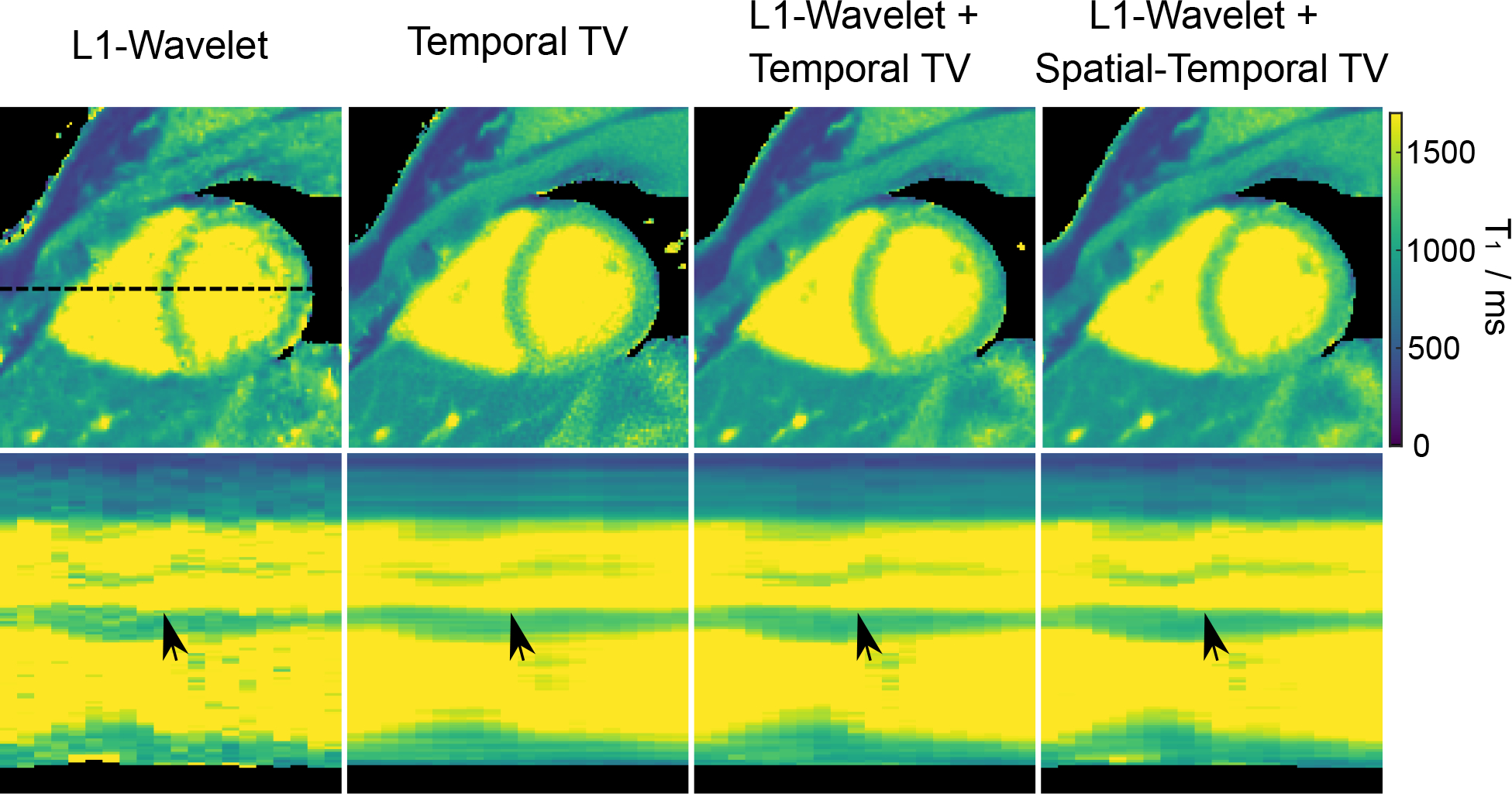
(Top) Myocardial T₁ maps (end-expiration and end-diastolic) with different types of regularization using the proposed motion-resolved model-based reconstruction. (Bottom) Horizontal profiles (dashed black line in the top) through all cardiac phases. The black arrows indicate subtle wall motion that is preserved best with the spatio-temporal TV regularization. Note that the regularization parameter α_min for each regularization type was tuned individually to achieve a fair comparison.

Figure 7(A) shows the effects of the minimum regularization parameter α_min on myocardial T₁ maps and the line profiles through the cardiac phases using the combination of the spatio-temporal TV and the spatial (ℓ₁-Wavelet) regularization. Figure 7 (B) presents the corresponding quantitative myocardial septal T₁ values for the ROI. As expected, both qualitative and quantitative results reveal that low values of α_min result in noisy maps (higher standard deviation) while high values may introduce blurring in the images. α_min = 0.005 was then chosen to balance noise reduction and preservation of anatomical details.

Figure 7.

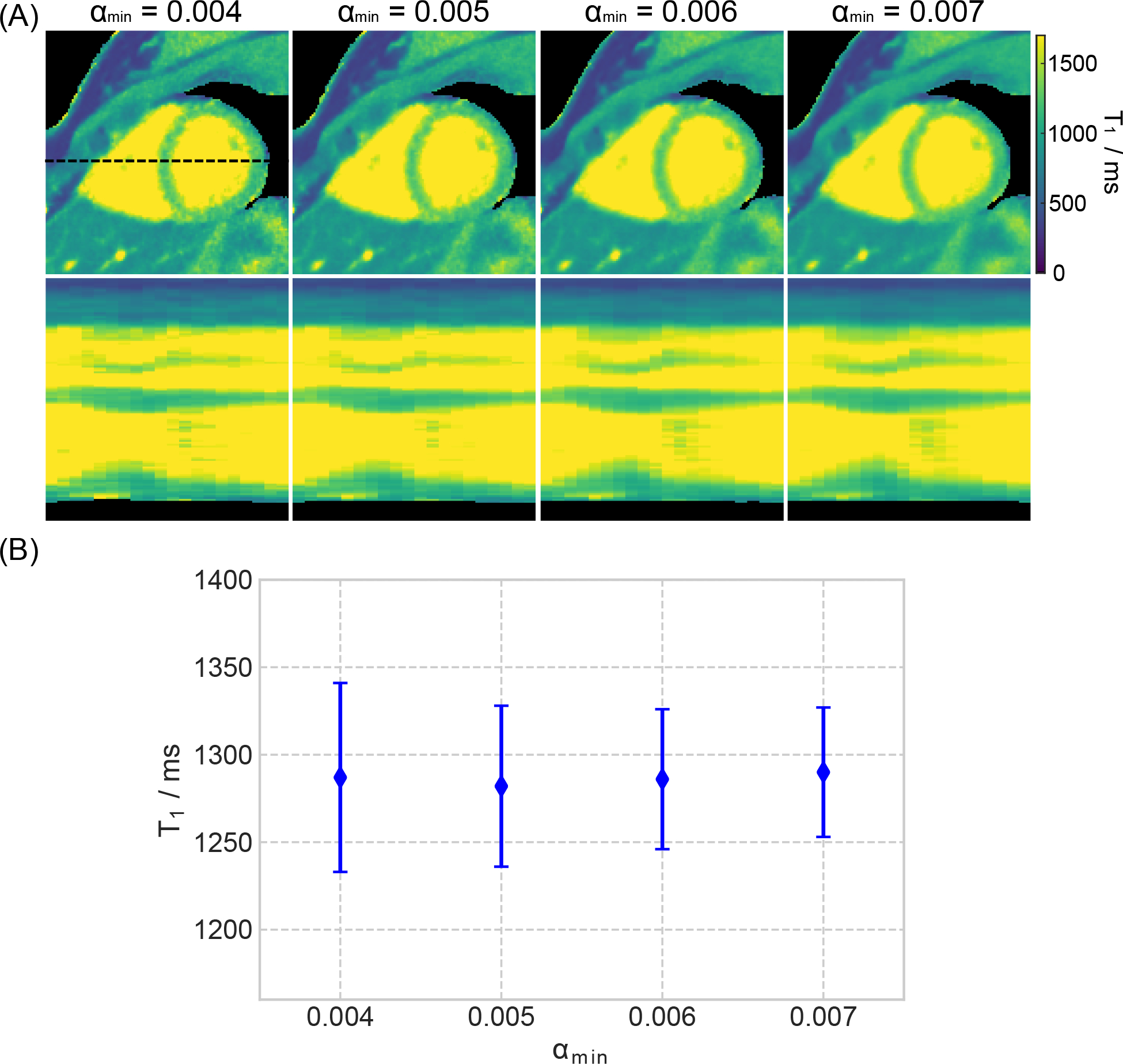
A. (Top) Myocardial T₁ maps (end-expiration and end-diastolic) estimated with motion-resolved model-based reconstruction with different choices of the minimum regularization parameter α_min. (Bottom) Horizontal profiles (dashed black line in the top) through all cardiac phases. B. Quantitative T₁ values (mean and standard deviation) within a ROI in the septal region.

With the above settings, Figure 8 shows a MOLLI T₁ map and two mid-ventricular myocardial T₁ maps at the end-diastolic and end-systolic phases (the same respiratory motion state) as well as the T₁ line profile through the cardiac phase using the proposed method for two representative subjects. Although the breathing conditions are different, diastolic myocardial T₁ maps are visually comparable between MOLLI and the free-breathing technique. Besides the diastolic T₁ map, the proposed method could also provide myocardial T₁ maps at other cardiac phases.

Figure 8.

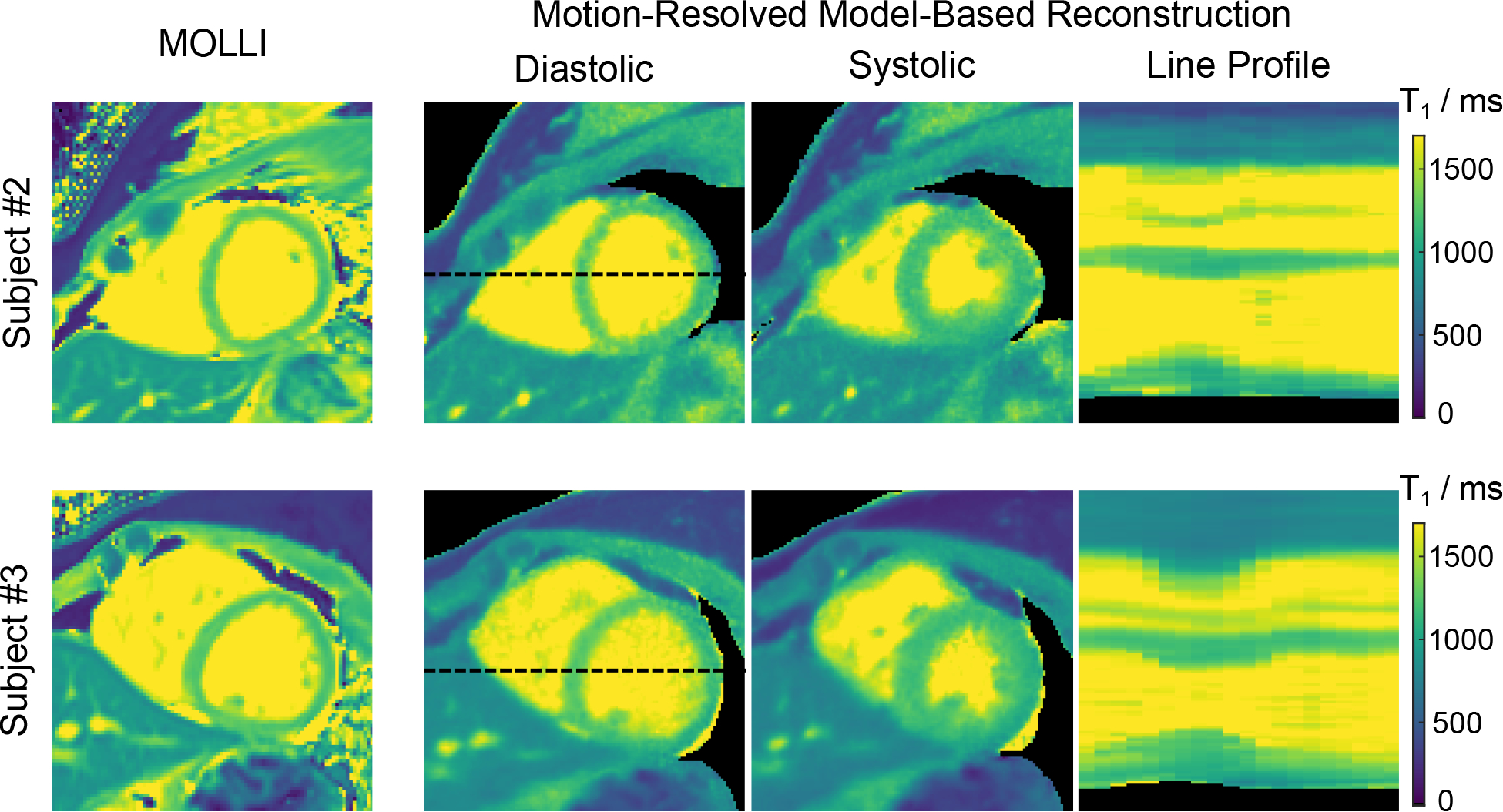
Diastolic and systolic myocardial T₁ maps (end-expiration) and line profiles through the cardiac phase of the motion-resolved model-based reconstruction acquired during free breathing in comparison to MOLLI acquired in a breathhold for two representative subjects.

The Supporting Information Figure S3 then presents two repetitive mid-ventricular myocardial T₁ maps (end-expiration and end-diastolic) of the proposed method and a MOLLI T₁ map for all subjects. Despite differences in breathing conditions between scans, the free-breathing T₁ maps are visually comparable between the two repetitive scans for all subjects. Figure 9 (A) shows the Bullseye plots of quantitative T₁ values and measurement repeatability errors for the six mid-ventricular segments of all subjects and scans for both the proposed motion-resolved model-based reconstruction and MOLLI techniques. Figure 9 (B) compares diastolic T₁ values for all mid-ventricular segments and septal segments (segments 8 and 9 according to AHA) for both methods. The paired t-test comparisons for each segment are summarized in the Supporting Information Table S3. The above quantitative comparison demonstrates that the proposed technique has slightly shorter mean T₁ values for all segments (1218 ± 56 ms vs 1231 ± 40 ms) but longer T₁ values for the septum segments (1262 ± 38 ms vs 1250 ± 28 ms) than MOLLI. However, no significant differences were found in most of the AHA segments, except for the lateral segments where MOLLI has longer T₁ values. Noteworthy, all the above T₁ values are within the published normal range at 3T [49]. Moreover, the proposed method has a slightly lower T₁ precision (higher CoV values) than MOLLI (CoV: 4.5% ± 1.4% vs 2.8% ± 1.1%, p < 0.01) but are comparable to MOLLI in the repeatability errors (34 ± 12 ms vs 31 ± 13 ms, p = 0.73) for all mid-ventricular segments. The Bland-Altman plot in the Supporting Information Figure S4 further reveal that the proposed T₁ correction formula generates longer T₁ values than the conventional Look-Locker correction technique (1262 ± 38 ms vs 1238 ± 35 ms, p < 0.01).

Figure 9.

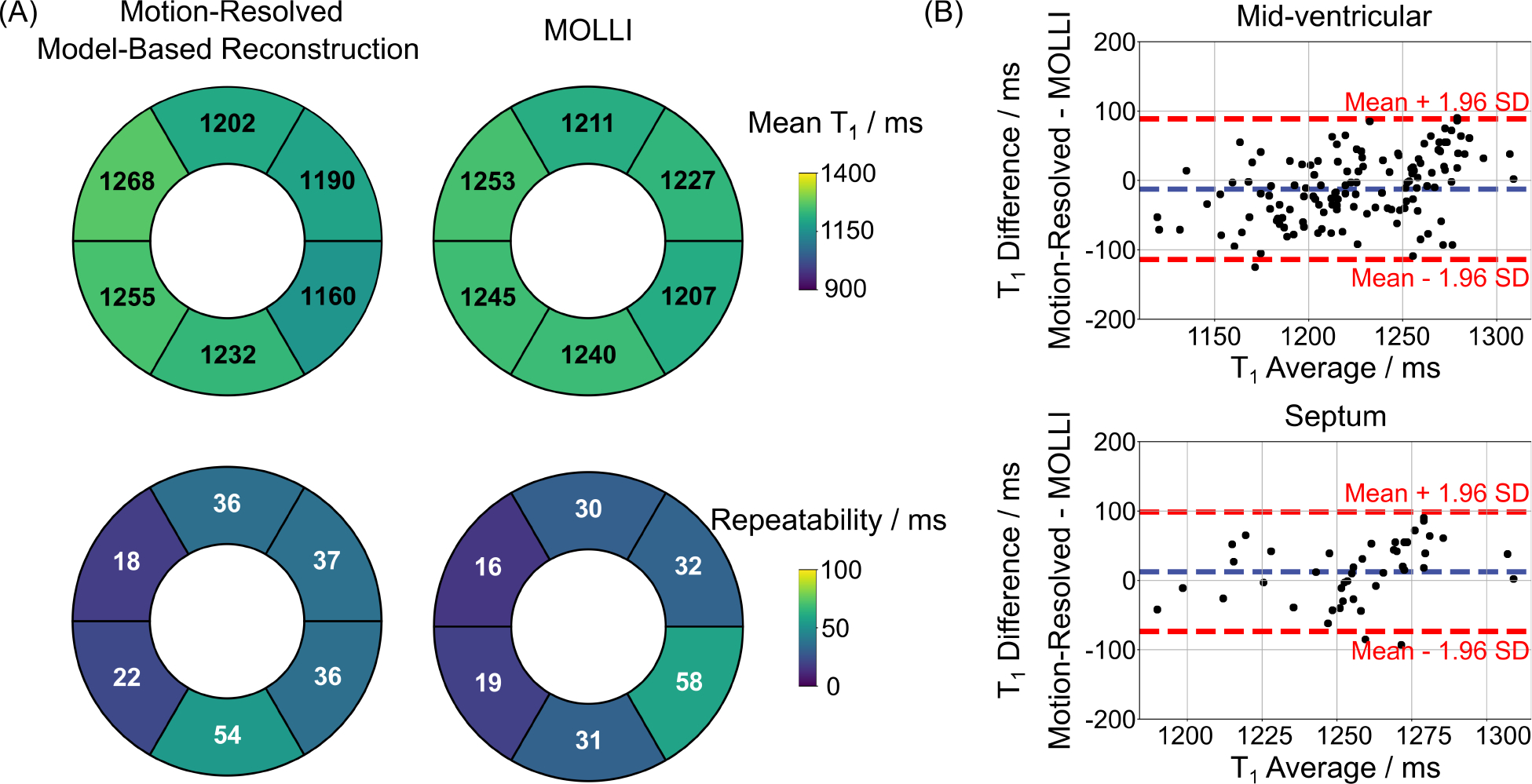
A. Bullseye plots of six mid-ventricular myocardial segments, showing (top) the mean diastolic T₁ values and (bottom) the measurement repeatability errors for all eleven subjects and all scans for (left) the motion-resolved model-based reconstruction (free-breathing) and (right) the MOLLI method (breathhold), respectively. B. Bland–Altman plots comparing the mean diastolic T₁ values of (top) all the six mid-ventricular segments (mean difference: −12 ms, SD: 52 ms) and (bottom) the septal segments (segments 8 and 9 according to AHA, mean difference: 12 ms, SD: 44 ms) for the proposed method and MOLLI for all subjects and scans.

Representative basal and apical diastolic myocardial T₁ maps, in addition to the mid-slice T₁ map, from two subjects, are shown in the Supporting Information Figure S5 (A). Quantitative results from both basal and apical slices and their comparison to MOLLI are presented in the Supporting Information Figure S5 (B) and (C). Again, although slight mean T₁ difference is observed between the motion-resolved model-based reconstruction and MOLLI techniques, no significant differences were found in all basal and apical AHA segments as shown in the Supporting Information Table S3. The Supporting Information Table S4 further shows the relative difference of the left-ventricular area calculated from the myocardial T₁ maps. We observe good repeatability (repeatability error: 3%) between scans. Although the results are obtained from a single slice, they are generally in the expected range for LVEF values. In addition, the quantitative T₁ maps and ROI-analyzed T₁ values in the Supporting Information Figure S6 demonstrate good agreement between the proposed approach and MOLLI for the pig experiment, i.e., both methods show higher and similar myocardial T₁ values in the infarcted septal and anterior wall regions, suggesting robustness of the proposed approach.

Aside from quantitative myocardial T₁ maps, Figure 10 presents synthesized T₁-weighted cardiac images (bright blood and dark blood) at the two cardiac phases for the same subjects shown in Figure 8. Both the bright-blood and dark-blood-weighted images clearly resolve the contrast between myocardium and blood pool. The synthetic images and myocardial T₁ maps at all cardiac phases were then converted into movies which are available as Supporting Information Videos S1 and S2. Similarly, a synthetic image series for all inversion times and all cardiac phases of one subject can be found in the Supporting Information Video S3.

Figure 10.

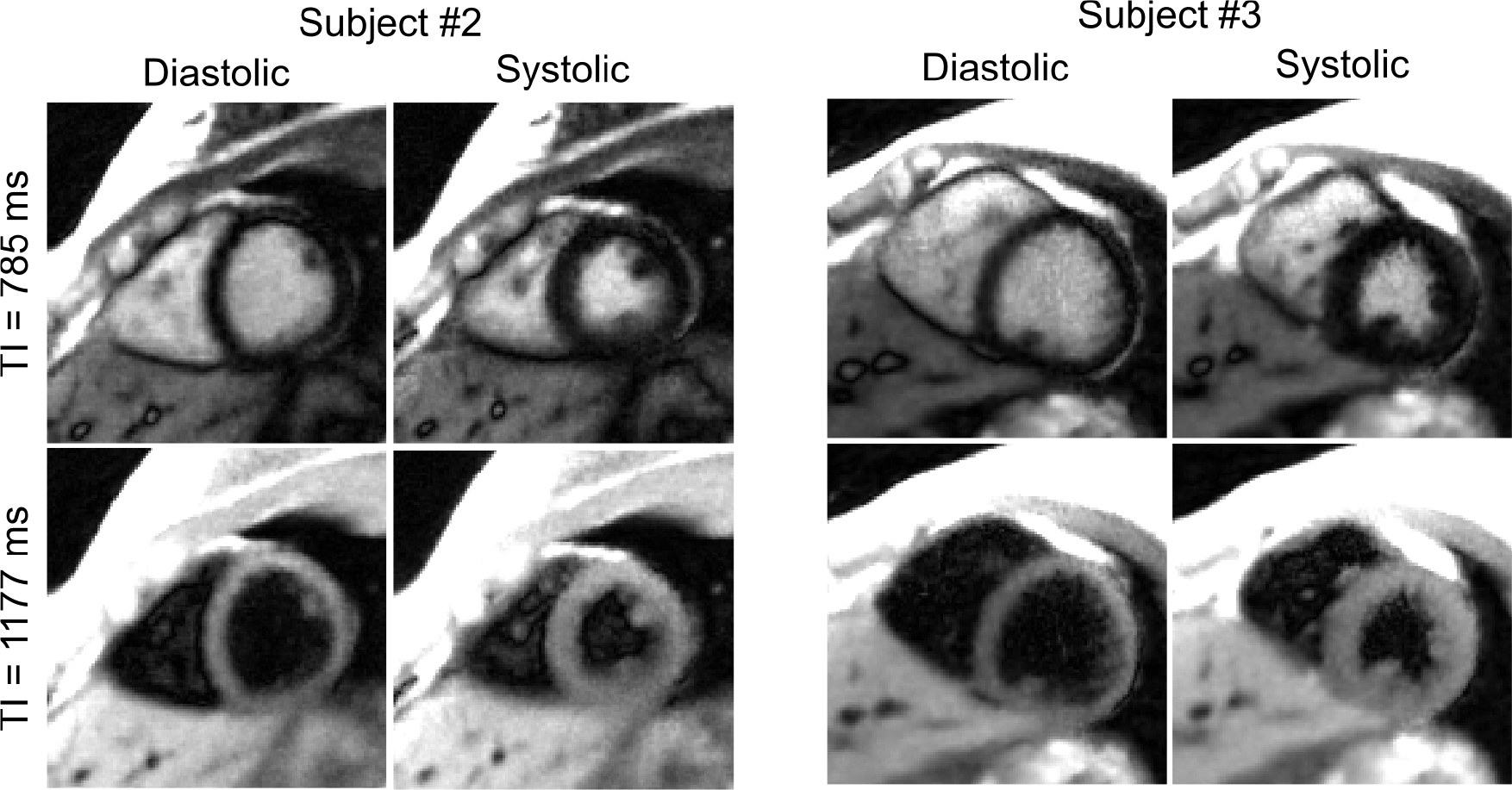
Synthesized T₁-weighted images at two representative inversion times (bright blood and dark blood) for the end-diastolic and end-systolic cardiac phases for the same subjects shown in Figure 8.

Discussion

In this work, we have developed a free-breathing high-resolution myocardial T₁ mapping technique using a free-running inversion-recovery radial FLASH sequence and a calibrationless motion-resolved model-based reconstruction. Instead of continuous acquisitions, we adopt a delay time between inversions to encode T₁ information and have derived a correction procedure for accurate T₁ estimation without needing full T₁ recovery or additional $B_1^{+}$ mapping. We further adapted the SSA-FARY strategy for robust respiratory motion signal estimation from the zero-padded AC region where the trajectory-dependent oscillations and contrast changing signal (due to inversion) have been eliminated in preprocessing. Following self-gating and data sorting, we propose to estimate both parameter maps and coil sensitivity maps of the desired motion states directly from k-space using an extended motion-resolved model-based reconstruction. The latter avoids any coil calibration and can employ high-dimensional spatio-temporal TV regularization, in addition to the spatial regularization, to improve precision in T₁ while preserving the spatio-temporal information. Studies have been performed on an experimental phantom, eleven healthy subjects and one young landrace pig with infarcted myocardium.

The phantom results demonstrate good T₁ accuracy of the proposed approach over a wide range of T₁ times. In vivo studies have shown similar diastolic myocardial T₁ values between the proposed approach and MOLLI for all segments, except for the lateral segments. The T₁ difference in the lateral regions between the two approaches and the difference between lateral and septal T₁ values can also be seen in other T₁ mapping techniques using continuous acquisitions, such as MR multitasking [15] and ref.[26]. The origin of these differences might be through-plane myocardial motion, which makes the lateral segments violate the assumed signal model. If new spins that experienced T₁ instead of $T_1^{*}$ relaxation move into the imaging plane due to the through-plane motion, the total signal intensity will increase, resulting in a faster signal recovery, i.e., a shorter apparent T₁ time. This is similar to the in-flow effects in blood T₁ estimation, as analyzed by Hermann et al. [50]. Although T₁ values in this work correspond well with MOLLI, the proposed approach may still underestimate T₁ when compared to the saturation recovery-based approaches such as SASHA and SAPPHIRE. With a low flip-angle FLASH readout, the proposed sequence should be robust to B₁ and slice profile effects [51]. The main contributing factor for the underestimation could be imperfect inversion caused by the non-selective hyperbolic secant pulse we used. The lateral regions are additionally affected by through-plane motion as explained above. The precision of the proposed method (CoV: 4.5% ± 1.4%) is lower than that of MOLLI (CoV: 2.8% ± 1.1%). Such a difference could be explained by the differences in the nominal spatial resolution (MOLLI: 1.4 × 1.4 × 8 mm³, the proposed: 1.0 × 1.0 × 6.0 mm³) and the readouts (MOLLI: Cartesian balanced SSFP, the proposed: radial FLASH). Nevertheless, the proposed approach shows comparable (CoV: 4.9% with 1.3 × 1.3 × 8 mm³ in ref. [26], CoV: 4.8% with 1.7 × 1.7 × 8 mm³ in MR multitasking [15]) or even slightly better (CoV: 5.7% with 1.6 × 1.6 × 8 mm³ in MRF [11]) T₁ precision when comparing to other well-known techniques.

Continuous acquisitions with constant flip angles [16, 17] have been used in several inversion-prepared free-running T₁ mapping techniques attributed to the scan efficiency. I.e., there is no waiting time between inversions. However, as pointed out by [19], continuous acquisition with the same flip angle only encodes $T_1^{*}$ information in the data [32]. Since $T_1^{*}$ is a function of flip angle and T₁, additional information about $B_1^{+}$ is therefore necessary for accurate T₁ estimation. However, the additional estimation of $B_1^{+}$ at the same motion state might be di cult to achieve in free-breathing, self-gated acquisitions. In [19], Zhou et al. propose to solve this issue by introducing a dual flip-angle strategy which acquires data continuously with two flip angles consecutively applied. Following self-gated data sorting, image reconstruction and dictionary matching, two different $T_1^{*}$ maps from the same motion state can be extracted and subsequently be used to calculate both T₁ and $B_1^{+}$ maps in an iterative manner. Most recently, a similar idea has been proposed in the MR multitasking technique for more accurate T₁ mapping [52]. Alternatively, in this work, we propose to resolve this problem by adopting a delay time between inversions, using this period for encoding T₁ information in the data. Different from studies which set the delay time long enough to ensure a full recovery of longitudinal magnetization, we are capable of estimating accurate T₁ even with incomplete T₁ recovery, shortening the acquisition time. Moreover, the proposed approach requires neither additional $B_1^{+}$ mapping nor the explicit calculation of $B_1^{+}$ from the data.

Self-gating constitutes another key component for free-breathing imaging. Although a few self-gating techniques have been successfully developed for steady-state imaging, estimation of reliable motion signals from the contrast-modulated k-space is challenging. In this work, following removal of signal oscillations in the k-space center signal, we model the additive and multiplicative effects caused by inversion in the data following [35] and propose to reduce such effects prior to the application of the SSA-FARY-based self-gating techniques. From our experience, the above step is crucial for reliable motion estimation using SSA-FARY. Although the proposed method could achieve robust respiration signal estimation, determination of reliable cardiac signals from the filtered k-space remained challenging and retrospective ECG gating was used for binning. Resolving the latter issue in future work would be valuable as the ECG signal is not always reliable [34], which we also observed for several data sets acquired for this study.

Inspired by the high-dimensional imaging techniques [15, 37, 53–55], we have sorted the data into multiple cardiac and respiratory motion states, and applied high-dimensional regularization along these motion dimensions to improve T₁ accuracy and precision. In contrast, several other studies [17, 19] combined data from multiple respiratory motion states into one using rigid image registration, following respiratory motion field being estimated from low-resolution images. The latter strategy has the advantage that more data is available for each cardiac phase than the one that sorts the data into multiple respiratory and cardiac motion states within the same amount of time. However, as motion between respiratory states is usually considered to be nonlinear [56] for cardiac imaging, a linear model may cause data mismatch in the cost function, resulting in reconstruction errors. Most recently, advanced nonlinear motion estimation methods have been developed for whole-heart coronary MR imaging [57]. Integration of such a nonlinear motion model into the model-based reconstruction framework would also be of great interest as it has the potential to shorten the total acquisition time of the proposed method while preserving good T₁ accuracy and precision.

Spatio-Temporal regularization has been shown to be more effective in exploiting sparsity in compressed-sensing reconstructions for dynamic/high-dimensional imaging, resulting in higher accelerator factors than spatial regularization-only reconstruction [15, 37, 53]. This work confirms the above findings in the regularized nonlinear model-based reconstruction for dynamic myocardial T₁ mapping. Moreover, our results demonstrate that the spatio-temporal TV regularization has a slightly better performance in both image denoising and preservation of structure details than the temporal TV regularization. On the other hand, although the regularization used in this study is effective in reducing noise/improving quantitative precision, it may also cause a certain degree of image blurring (lower effective spatial resolution) similar to other regularization techniques used in compressed sensing. More advanced regularization, such as neural network-enhanced regularizers [58] could be employed in future studies to solve this issue.

The proposed method takes around two minutes for reliable T₁ estimation, which compares well to alternative techniques when considering the relatively high nominal resolution of the T₁ maps (1.0 × 1.0 × 6 mm³). The acquisition time could be shorted by further reducing the delay time. Here, we adopted the three-second delay to achieve a good compromise of T₁ accuracy and precision. However, in principle, a delay time of one second could be used (at a cost of lower precision), resulting in acquisition times of around 80 s.

There are also other limitations of the present work that need to be mentioned. First, the blood T₁ estimated by methods using continuous acquisition may not be reliable as the in-flow effects make the blood violate the assumed signal model, a problem which also affects other methods based on continuous acquisition [17, 19, 50]. Thus, the proposed method is not ideal for estimating the extracellular volume (ECV). A thorough investigation of how blood T₁ is affected by the proposed sequence using simulations and a flow phantom, similar to the work in [50], would be an interesting next step. Second, evaluation of the proposed method has so far only been done in healthy volunteers. Validation of the proposed free-breathing method in patient studies with both native and post-contrast T₁ mapping is now warranted and will be the subject of future work. Another limitation of the proposed method is the long computation time. Although substantial efforts have been made in the implementation part to enable model-based reconstruction to run on GPUs, which already reduced reconstruction time from several hours to 25 minutes, further efforts are still needed.

Conclusion

The proposed free-breathing method enables high-resolution T₁ mapping with good T₁ accuracy, precision and repeatability by combing inversion-recovery radial FLASH, self-gating and a calibrationless motion-resolved model-based reconstruction.

Supplementary Material

vS1

Supporting Information Video S1. Synthesized T₁-weighted image series (bright blood and dark blood) and the corresponding myocardial T₁ maps through the cardiac phase dimension for subject #2.

supinfo

Supporting Information Figure S1. A. Bland-Altman plots comparing ROI-analyzed phantom T₁ values (top) between the original Look-Locker correction and the IR spin-echo reference (from left to right, mean difference: −50, −57, −74, −108 and −195 ms, and SD: 14, 24, 45, 85 and 163 ms), and (bottom) between the proposed correction and the IR spin-echo reference (from left to right, mean difference: −21, −22, −26, −26 and −41 ms, and SD: 11, 10, 12, 11 and 19 ms) for various delays. B. Bland-Altman plots comparing ROI-analyzed phantom T₁ values between motion-resolved model-based reconstruction with different regularizations and the IR spin-echo reference (from left to right, mean difference: −31, −31 and −31 ms, and SD: 12, 12 and 12 ms).

Supporting Information Figure S2. (Top) One of the “end-diastolic” images (28th of 32) of a simulated dynamic image series and (middle and bottom) the corresponding horizontal profiles (dashed line in the top) through the motion dimension. The image series were reconstructed using the motion-resolved image reconstruction with different regularization type.

Supporting Information Figure S3. Two repeated myocardial T₁ maps (end-expiration, end-diastolic) of the motion-resolved model-based reconstruction acquired during free breathing in comparison to MOLLI acquired in a breathhold for all eleven subjects.

Supporting Information Figure S4. Bland-Altman plots comparing ROI-analyzed mid-ventricular septal mean T₁ values between the proposed correction and the Look-Locker correction for all subjects and scans. The mean difference is 24 ms and SD is 8 ms.

Supporting Information Figure S5. A. Representative diastolic T₁ maps of basal, mid and apical short-axis slices reconstructed with the motion-resolved model-based reconstruction (free breathing) for two healthy subjects. B. Bullseye plots of (top) six basal segments and (bottom) four apical segments, showing the mean diastolic T₁ values for six subjects for (left) the motion-resolved model-based reconstruction acquired during free breathing and (right) the MOLLI reference acquired in a breathhold. C. Bland Altman plots comparing (top) the mean diastolic T₁ values of all six basal segments (mean difference: −15 ms, SD: 45 ms) and the two basal septal segments (segments 2 and 3 according to AHA, mean difference: 9 ms, SD: 42 ms), and (bottom) the mean diastolic T₁ values of all apical segments (mean difference: −3 ms, SD: 71 ms) and the one apical septal segment (segment 14 according to AHA, mean difference: 42 ms, SD: 40 ms) for the proposed method and MOLLI for six subjects.

Supporting Information Figure S6. Free-breathing systolic and diastolic myocardial T₁ maps reconstructed with the motion-resolved model-based reconstruction and their comparison to the MOLLI reference for a pig experiment. The ROI-analyzed mean T₁ values (ms) and CoV values (%) for all the mid-ventricular AHA segments are presented in the bottom.

Supporting Information Table S1. T₁ relaxation times (ms, mean ± SD) and CoV values (%) for the experimental phantom in Figure 2.

Supporting Information Table S2. T₁ relaxation times (ms, mean ± SD) and CoV values (%) for the experimental phantom in Figure 3.

Supporting Information Table S3. The P-value of paired t-test comparison of the proposed free-breathing diastolic T₁ values and MOLLI T₁ values in each AHA segment.

Supporting Information Table S4. The relative difference (%) of the left-ventricular area between end-diastolic and end-systolic mid-ventricular myocardial T₁ maps for all subjects and scans.

vS2

Supporting Information Video S2. Synthesized T₁-weighted image series (bright blood and dark blood) and the corresponding myocardial T₁ maps through the cardiac phase dimension for subject #3.

vS3

Supporting Information Video S3. Synthesized T₁-weighted image series at temporal resolution of 49 ms for all inversion times and all cardiac phases of subject #2.

Appendix I: IRGNM-ADMM algorithm

In the above algorithm, $\mathbf{p}\mathbf{r}\mathbf{o}{\mathbf{x}}_{{\alpha }_n/\rho }^{\mathbf{m}}$ contains the following three proximal operators:

$$Z_{\mathit{m}}^{k+1}:=W^H{S}_{{\alpha }_n/\rho }\left(W{Z}_{\mathit{m}}^k\right)\left(\text{Wavelet-domain}\text{joint}\text{soft-thresholding}\right)$$

$$Z_{\mathit{m}}^{k+1}:=P_S\left(Z_{\mathit{m}}^k\right)\left(\text{projection}\text{of}{Z}_{\mathit{m}}^k\text{onto}\text{domain}S\right)$$

$$Z_{\mathit{m}}^{k+1}:=D^H{S}_{{\alpha }_n/\rho }D{Z}_{\mathit{m}}^k\left(\text{Total}\text{variation}\text{gradient-domain}\text{soft-thresholding}\right)$$

and $\mathbf{p}\mathbf{r}\mathbf{o}{\mathbf{x}}_{{\alpha }_n/\rho }^{\mathit{c}}$ is the least-square proximal operator, i.e.,

$$Z_{\mathit{c}}^{k+1}:=\frac{1}{2}{Z}_{\mathit{c}}^k.$$

Data Availability Statement

In the spirit of reproducible research, code to reproduce the experiments will be available on https://github.com/mrirecon/motion-resolved-myocardial-T1-mapping. The raw k-space data, all ROIs to reproduce the quantitative values and other relevant files used in this study can be downloaded from https://doi.org/10.5281/zenodo.5707688.