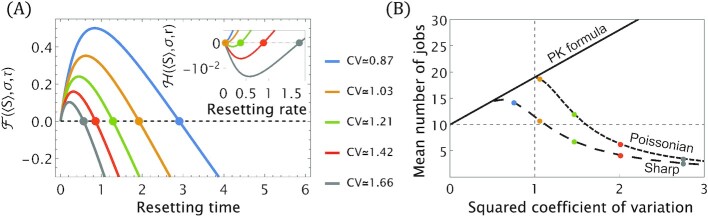
Fig. 5.

Panel (A): solutions of Eqs. (29) and (30) for the Log-normal service time distribution under Poissonian (inset) and sharp resetting (main). Here, we fix 〈S〉 = 1 for the mean service time without resetting and vary σ to control relative stochastic fluctuations, CV, via Eq. (28). The intersection points of the curves with the dashed horizontal line going through the origin give the optimal resetting times τ* (optimal resetting rates r* in the inset). Note that higher values of σ yield lower optimal resetting times (higher resetting rates). Panel (B): The mean number of jobs in a queue with arrival rate λ = 0.95, as a function of the underlying CV² of the service time distribution. The Pollaczek–Khinchin formula gives the familiar linear dependence of Eq. (1). Also plotted are the behaviors for the optimal Poissonian and sharp resetting protocols, with colored circles matching their counterparts in panel (A). Strong deviations from the Pollaczek–Khinchin behavior of the nonrestarted case are observed. While resetting provides no advantage for low CV values, it can drastically reduce queue lengths when CV is high.