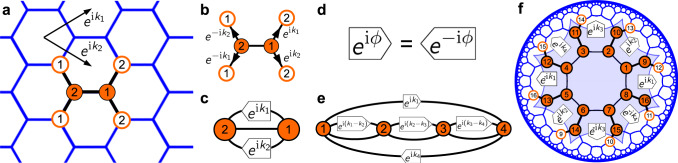
Fig. 1. Unit-cell circuits.

a Euclidean {6, 3} honeycomb lattice with two sites in the unit cell (full orange circles). Each site has 3 neighbors, some of them in adjacent unit cells (empty orange circles). b The wave function of particles hopping between unit cells picks up a complex Bloch phase, see Eq. (1). c The associated unit-cell circuit diagram encodes the Bloch-wave Hamiltonian H(k), Eq. (2), and the energy bands. Momentum k = (k₁, k₂) is an external parameter. d In topolectrical circuits, a complex-phase element imprints tunable Bloch phases along edges connecting neighboring sites. The circuit element is directed, with e^iϕ imprinted in one direction, and e^−iϕ in the other. This leads to Hermitian matrices H(k). Unit-cell circuits for the {8, 4} (e) and {8, 3} (f) hyperbolic lattices. The Bravais lattice is the {8, 8} lattice in either case, with 4 and 16 sites in the unit cell, respectively. In these lattices, Bloch waves carry a four-dimensional momentum k = (k₁, k₂, k₃, k₄).