Cerebral hemodynamics during atrial fibrillation: Computational fluid dynamics analysis of lenticulostriate arteries using 7 T high-resolution magnetic resonance imaging

Abstract

Atrial fibrillation (AF) is the most common cardiac arrhythmia, inducing irregular and faster heart beating. Aside from disabling symptoms—such as palpitations, chest discomfort, and reduced exercise capacity—there is growing evidence that AF increases the risk of dementia and cognitive decline, even in the absence of clinical strokes. Among the possible mechanisms, the alteration of deep cerebral hemodynamics during AF is one of the most fascinating and least investigated hypotheses. Lenticulostriate arteries (LSAs)—small perforating arteries perpendicularly departing from the anterior and middle cerebral arteries and supplying blood flow to basal ganglia—are especially involved in silent strokes and cerebral small vessel diseases, which are considered among the main vascular drivers of dementia. We propose for the first time a computational fluid dynamics analysis to investigate the AF effects on the LSAs hemodynamics by using 7 T high-resolution magnetic resonance imaging (MRI). We explored different heart rates (HRs)—from 50 to 130 bpm—in sinus rhythm and AF, exploiting MRI data from a healthy young male and internal carotid artery data from validated 0D cardiovascular-cerebral modeling as inflow condition. Our results reveal that AF induces a marked reduction of wall shear stress and flow velocity fields. This study suggests that AF at higher HR leads to a more hazardous hemodynamic scenario by increasing the atheromatosis and thrombogenesis risks in the LSAs region.

NOMENCLATURE

ACA

Anterior cerebral artery

AF

Atrial fibrillation

CFD

Computational fluid dynamics

FV

Flow velocity

HR

Heart rate

ICA

Internal carotid artery

LSAs

Lenticulostriate arteries

MCA

Middle cerebral artery

MRI

Magnetic resonance imaging

Q

Flow rate

RR

Heartbeat interval

SR

Sinus rhythm

WSS

Wall shear stress

I. INTRODUCTION

Atrial fibrillation (AF), characterized by an irregular and faster heart beating, is the most common cardiac arrhythmia with nearly 60 × 10⁶ prevalent cases worldwide in 2019¹ and, due to rising life expectancy in Western countries, its incidence is expected to more than double within the next 40 years.² Through a constellation of potential underlying hemodynamic mechanisms—such as silent microembolic cerebral infarctions, altered cerebral blood flow, hypoperfusion, and microbleeds^3–6—there is recent growing evidence that AF is independently associated with an increased risk of dementia and cognitive impairment,^3,7,8 even in the absence of clinical strokes.^9,10 However, a clear causal link between AF and cognitive decline still lacks⁷ and, among the possible contributors, the hypothesis of an altered cerebral blood flow at the distal level is the most intriguing and the least investigated.^3,4 In particular, silent strokes and cerebral small vessel diseases are believed to be among the main vascular drivers of cognitive decline and dementia. Within this context, lenticulostriate arteries (LSAs), i.e., small perforating arteries (0.1–1.5 mm diameter) supplying blood flow to important subcortical and basal ganglia areas—require special attention. Indeed, being small end arteries perpendicularly departing from the anterior (ACA) and the middle cerebral (MCA) arteries, the LSAs are prone to hemodynamic alterations, ranging from hypoxia conditions to lacunar strokes (i.e., ischemic strokes located in the LSAs).^11,12

Recent low-order computational approaches trying to fill current knowledge gaps highlighted that the repeated exposure to irregular AF beating promotes alterations of the hemodynamic patterns in the distal cerebral circulation during AF.¹³ Critical episodes, either hypoperfusions or hypertensive events, could induce potential damage via reduced cerebral blood flow or hemorrhagic episodes,^14,15 especially in case the heart rate (HR) ranges out of the 50 < HR < 70 bpm reference interval.¹⁶ More recently, high-frequency near-infrared spectroscopy monitoring in vivo confirmed the computational hypotheses, showing a beat-to-beat level that sinus rhythm (SR) restoration after electrical cardioversion significantly improved cerebral microcirculation.¹⁷

One of the reasons why, to date, well-established causal links between AF hemodynamics and cognitive impairment are missing is the difficulty in obtaining direct and local clinical measures: currently adopted techniques usually fail in capturing the cerebral micro-vasculature hemodynamics. In particular, transcranial Doppler ultrasonography¹⁸ lacks the resolving power to provide insight in terms of flow and pressure signals on the portion downstream the three cerebral arteries (anterior, middle, and posterior). 4D flow magnetic resonance imaging (MRI) is able to describe in detail the flow of the large cerebral arteries and can even be pushed to small distal cerebral arteries beyond the circle of Willis.¹⁹ However, 4D MRI is currently not able to assess blood flow in the penetrating arteries and also cannot provide direct wall shear stress (WSS) information, which is just as significant as the flow field. At the same time, lumped and one-dimensional cerebrovascular models, although useful to grasp AF effects on the global cerebral hemodynamics, are not adequate to examine local variations and spatial details of the flow structure due to AF. 3D computational fluid dynamics (CFD) methods based on MRI are instead definitely suitable to study the local hemodynamics by relying on clinically measured 3D vascular morphologies. Once the vessel centerline is identified, 2D segmentations of the vessel lumen are created and merged together to form the complete 3D model of the vascular anatomy. After being coupled with low-order (0D–1D) dimensional models to impose suitable boundary conditions, the three-dimensional continuity and momentum Navier–Stokes equations are discretized over the computational domain and usually solved by finite element/volume methods. In so doing, the temporal evolution of the 3D flow velocity (FV) and pressure fields over the whole spatial domain are obtained, making CFD based on MRI particularly promising to investigate brain blood flow, given the complexity and variability of the geometrical topology, flow patterns, and stresses of the cerebral hemodynamics.²⁰ CFD analyses already proved to be a powerful tool to inquire into AF effects on the local hemodynamics and have been employed for the aortic^21,22 and left atrium regions.^23–25 However, to the best of our knowledge, CFD analyses of the LSAs in AF conditions have not been performed so far. CFD analyses of the LSAs are overall very few, mostly due to the difficulty of achieving high-resolution MRI through which building a reliable computational domain: available literature mainly focuses on stenotic and acute ischemic stroke conditions,^26,27 also resorting to ideal two-dimensional models.²⁸

In the present work, we propose for the first time a CFD analysis to investigate the AF effects on the LSAs hemodynamics by using 7 T high-resolution MRI²⁹ to reconstruct the cerebral geometry. The main AF features, namely, the absence of atrial kick and the uncorrelated, faster, and more variable heart beating—were taken into account by exploiting data from our validated 0D cardiovascular-cerebral modeling¹⁶ as inlet condition for the 3D CFD model. The CFD analysis was performed using Simvascular, open-source software implementing a finite element method, which is widely adopted for 3D computational hemodynamics and particularly suitable for image-based cardiovascular simulations.^30,31 In particular, different HRs, from 50 to 130 bpm, in SR and AF conditions were explored to define the internal carotid artery (ICA) flow rate, Q_ICA, inlet conditions. Being a CFD analysis on a fully 3D domain over thousands of beats computationally unfeasible—long time series are necessary to significantly reproduce the statistical properties of AF, we separately considered two different kinds of ICA inlet conditions: (case A) constant flow rate Q_ICA, taken by spanning the range of flow rate values reached through the 0D cardiovascular-cerebral modeling over thousands of beats at each mean HR; (case B) periodic pulsatile flow rate waveform, $Q_{\mathit{ICA}}(t)$, over a single typical beat of the HR considered. In so doing, we separately accounted for the two main AF beating features: (case A) the effects of heart rhythm, namely, the increased variability of cardiac beats (and then wider Q_ICA range) in AF with respect to SR; (case B) the effects of heart rate at the single beat scale, as cardiac beats in AF occur at a faster rate, inducing a different shape of the $Q_{\mathit{ICA}}(t)$ signal. In both cases A and B, the results were expressed in terms of wall shear stress (WSS) and flow velocity (FV), which turned out to be the most meaningful fluid dynamics metrics. Present findings show significant AF-induced changes in the deep cerebral circulation and demonstrate the key role of fluid dynamics simulations in shedding light on complex mechanisms underlying important cerebral pathologies.

II. METHODS

A. Magnetic resonance imaging and reconstructed geometry

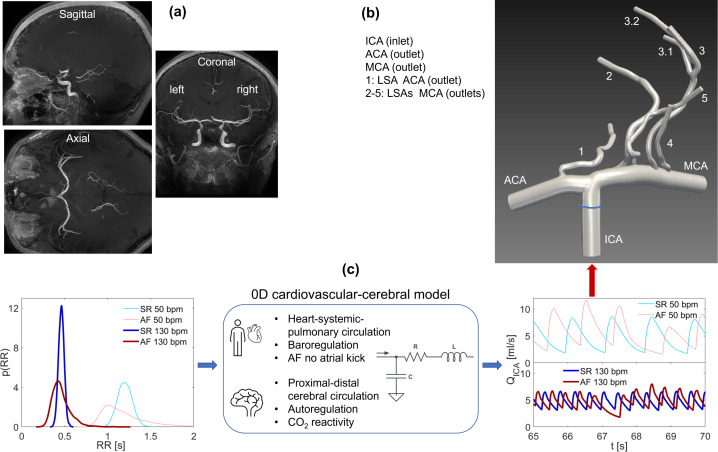
MRI data of a 20 years old healthy male subject, acquired within a group of ten volunteers using a 7 T MRI scanner (Philips Healthcare, Cleveland, OH) at the Brain Center, University Medical Center Utrecht, Utrecht (The Netherlands), were used to reconstruct the cerebral anatomy. The study protocol was approved by the local institutional review board, and all subjects were scanned after written informed consent. High-resolution three-dimensional T1-, T2-, as well as T2^*-weighted sequences and time-of-flight angiography were used to extract morphological information on the circle of Willis and perforating LSAs. In particular, the vasculature geometry was built based on the 3D T1-weighted magnetization prepared rapid gradient echo sequence with acquired and reconstructed resolutions (mm) of (0.5 × 0.5 × 0.5) and (0.29 × 0.29 × 0.25), respectively. Full details of scan parameters and volunteers are offered elsewhere,²⁹ while Fig. 1(a) shows the three (axial, coronal, sagittal) planes describing the anatomical vascular structures of the selected healthy volunteer.

FIG. 1.

Scheme of the model construction: (a) MRI anatomy data view through axial, coronal, and sagittal planes; (b) 3D model geometry with inlet and outlet boundary conditions; (c) RR pdfs (SR and AF, 50 and 130 bpm), schematic features of the 0D cardiovascular-cerebral model, and resulting ICA flow rate time-series, $Q_{\mathit{ICA}}(t)$ (SR and AF, 50 and 130 bpm).

The geometry was reconstructed from raw MRI data in the DICOM format exploiting the Simvascular (Version 22.02.09) image-based modeling pipeline,³⁰ which consists in identifying the vessel centerline, creating 2D segmentations of the vessel lumen (perpendicular to the centerline path), generating 3D surfaces fitted to groups of 2D segmentations, and eventually joining together single vessels to form the complete 3D model of the vascular anatomy. The resulting 3D geometry is shown in Fig. 1(b) and comprises the right internal carotid artery (ICA), the precommunicating ACA, the MCA, and 5 LSAs perpendicularly departing from MCA (four vessels) and ACA (one vessel) with inlet diameters 0.9 mm (LSAs 1–3), 1.0 mm (LSA 4), and 0.8 mm (LSA 5).

B. Governing equations, boundary conditions, and numerical simulation

Blood was assumed as an incompressible, homogeneous, and Newtonian fluid, characterized by constant density, ρ, and dynamic viscosity, μ, while the effects of suspended particles were neglected. Since LSAs diameter here averagely ranges between 0.8 and 1.0 mm, the particle size ( $\sim \mu$m) is still negligible with respect to the vessel diameter; thus, the Newtonianity and homogeneity of the fluid hold valid.³² The Newtonian hypothesis was adopted considering that the same assumption was done in the available literature performing CFD analyses of the LSAs.^26–28 Moreover, in the cerebral circulation—starting from the carotid sinus up to the circle of Willis circulation—Newtonian and non-Newtonian assumptions led to minor differences in the flow characteristics, also due to the reduced flow pulsatility.^33,34 In addition, a comparison between Newtonian and non-Newtonian models in the circle of Willis showed the same spatial distribution of WSS with slightly higher values in the non-Newtonian model.³⁵ In the end, although modest differences may emerge between Newtonian and non-Newtonian models, we here use the same Newtonian hypothesis to compare AF and SR conditions, which show much more significant differences than any neglected non-Newtonian effect (i.e., the non-Newtonian model would slightly and similarly affect both AF and SR configurations). Under these hypotheses, the blood flow is governed by the three-dimensional continuity and momentum Navier–Stokes equations, expressed as follows:

$$\frac{\partial u_i}{\partial x_i}=0,$$ (1)

$$\frac{\partial u_i}{\partial t}+u_j\frac{\partial u_i}{\partial x_j}=-\frac{1}{\rho }\frac{\partial p}{\partial x_i}+\nu \frac{{\partial }^2{u}_i}{\partial x_j^2},$$ (2)

where x_i and u_i denote in index notation (i = 1, 2, 3) the Cartesian coordinates (x, y, z) and the velocity components (u, v, w), respectively, p is the pressure, ρ = 1060 kg/m³ is the blood density, and ν = 3.77 × 10⁻⁶ m²/s is the blood kinematic viscosity.

The model consists of one inlet (ICA) and nine outlets (ACA, MCA, and seven LSA outflows) as displayed in Fig. 1(b). The ICA inlet condition was given in terms of flow rate, Q, extracted from a 0D cardiovascular-cerebral model already validated and used to inquire the hemodynamic AF effects on the cerebral circulation at different HRs.^13–16 Two kinds of inflow conditions will be obtained from the 0D cardiovascular-cerebral model [see Fig. 1(c)]: (case A) constant flow rate, taken by spanning the range of maximum values typically reached by different flow rate time-series [as shown in Fig. 1(c)] at each HR; (case B) periodic pulsatile flow rate waveform over one beat defined by the considered HR [Fig. 1(c) shows representative flow rate time-series over variable beats]. Outflow conditions were treated through the weakly prescribed pressure boundary by setting to zero the outlet pressure. All vessels were assumed to be rigid and with time-independent geometry, no-slip condition was applied to the wall boundaries. The mean Reynolds number Re—defined through the blood kinematic viscosity ν, the bulk velocity U, and the vessel diameter D at the outlet—is $Re\approx {10}^2$ for the MCA and $Re\approx {10}^1$ for the LSAs.

The continuity and momentum Navier–Stokes equations (1) and (2) were discretized and numerically solved by means of Simvascular (Version 22.02.09), which is open-source software implementing a finite element method (http://simvascular.github.io/). Simvascular is particularly suited for image-based cardiovascular CFD, as it provides a complete pipeline from medical image data segmentation to patient-specific blood flow simulation and analysis.³⁰

One of the reasons why Simvascular was chosen and its primary advantage with respect to other existing software is the integration and complete handling of the geometry segmentation, meshing capabilities, coupling with reduced order models, and numerical resolution into one computational tool (only post-processing is carried out with Paraview), which facilitates the patient-specific project and decreases the time needed for numerical investigations.^36,37 Moreover, the algorithms implemented by Simvascular are, together with the VMTK platform (http://www.vmtk.org/), among the most optimized and adopted for the 3D reconstruction of image-based blood vessel models. In terms of predicting results, given the same simulation conditions, agreement among Ansys Fluent, FEBio, and Simvascular was remarkably good in terms of WSS for the carotid bifurcation,³⁸ while COMSOL Multiphysics, Ansys Fluent, and Simvascular could predict flow and pressure waveforms without any notable differences for the thoracic aortic hemodynamics³⁹ as well as both Ansys Fluent and Simvascular accurately and similarly predicted the complex flow patterns in the abdominal aorta flow,³⁶ Glenn anastomosis, and central shunt pulmonary models.⁴⁰ For all the above reasons, Simvascular has become paradigm software for 3D computational hemodynamics and cardiovascular modeling research, adopted for CFD analyses at high-to-moderate Reynolds numbers investigating the hemodynamics of aortic pathologies,^41–43 thus perfectly able to capture the LSAs hemodynamics at lower Reynolds numbers. Given its well-established employment in cardiovascular applications and considering the efficiency and accuracy of image-based handling, Simvascular is here adopted for the present CFD analysis. To further strengthen and validate our choice of adopting Simvascular, in the supplementary material a test case—namely, the laminar flow in a curved tube—is reported, comparing results obtained through Simvascular with different CFD investigations and analytical approximations. In the following, we report the main computational features of Simvascular, while further details are offered elsewhere.^30,31 The streamline-upwind/Petrov–Galerkin and pressure-stabilizing/Petrov–Galerkin formulation leads to the weak form of the Navier–Stokes equations (1) and (2), which reads

$$\begin{array}{c}{B}_G(w_i,q;u_i,p)\\ =+{\int }_{\Omega }\left\{w_i\rho \left(\frac{\partial u_i}{\partial t}+u_j\frac{\partial u_i}{\partial x_j}\right)+\frac{\partial w_i}{\partial x_j}\left(\mu \frac{\partial u_i}{\partial x_j}-p\right)-q_i{u}_i\right\}d\Omega \\ +{\int }_{{\Gamma }_N}\left\{w_i\left(-\mu \frac{\partial u_i}{\partial n_j}+p{n}_i\right)+q{u}_i{n}_i\right\}d\Gamma =0,\end{array}$$ (3)

where $\Omega \in {ℝ}^3$ is the domain with boundary $\Gamma ={\Gamma }_D\cup {\Gamma }_N$ (Dirichlet conditions are applied on Γ_D, while Neumann conditions on Γ_N), n_i is the normal vector to Γ, and w_i and q are weight functions defined in the space functions $W=\{w_i\in {[H^1(\Omega )]}^d:w_i=0$ on ${\Gamma }_D\}$ and $Q=L^2(\Omega )$, respectively. Both the momentum and pressure stabilization terms are included, the first required to handle advection dominated flows and the latter to support the use of linear tetrahedral elements as well as incompressibility constraint is also stabilized. The resulting stabilized weak form of the Navier–Stokes equations is

$$B(w_i,q;u_i,p)=B_G(w_i,q;u_i,p)+\mathit{mps}+\mathit{ics}+cs,$$ (4)

where mps is a momentum and pressure stabilization term and ics is an incompressibility constraint stabilization term, while cs is a compensation for the stabilization term.³⁰ The stabilized FEM formulation reported in Eq. (4) is discretized in time using the generalized alpha time-stepping scheme, here set to a second-order scheme satisfying CFL criterion. Convergence criteria were based on the residual norm of the numerical solution with the threshold here set equal to 10⁻⁵. The maximum number of nonlinear iterations for each time step, usually taken equal to 1–2 for steady simulations and at least 3 for pulsatile configurations,^30,31 is here increased to 7 to guarantee a more accurate solution at an acceptable computational cost. Apart from the higher computational cost, no significant changes emerge with a number of nonlinear iterations higher than 3. For both pulsatile and steady simulations, stable numerical convergence of the solution was achieved after an initial numerical transient of about 0.06 s. Since for steady simulations, the flow rate was taken constant and by spanning, for each run, the range^2,14 ml/s, the time step size is constant and taken equal to 0.05 ms to guarantee for all the runs the numerical convergence to steady solution in 1200 time steps and avoid numerical fluctuations for simulations at higher constant flow rate values. For pulsatile simulations, once the initial numerical transient is extinguished, a larger time step size (0.2 ms) can be adopted, as high flow rate values are reached only once in a heartbeat in correspondence of the systolic peak. Lower time step size values did not lead to significant changes.

Suitable flow domain extensions (from 3D to 5D, where D is the vessel diameter) were added to the inlet [highlighted in blue in Fig. 1(b)] and the outlets to guarantee a fully developed flow field. SimVascular supports construction of unstructured tetrahedral meshes based on the open-source TetGen kernel, combining exact constrained Delaunay tetrahedralizations, boundary conforming Delaunay meshes, and Voronoi partitions, together with functionalities such as adaptive meshing, boundary layer, and radius-based meshing. To accurately capture the variety of the flow features (e.g., recirculating regions far from the walls as well as velocity field attached and parallel to the walls, stagnation points, and flow separation) throughout the domain and given the low Reynolds numbers involved, the computational domain is composed of uniform tetrahedral elements. The global maximum edge size is set equal to 0.017 cm with a minimum volume of the elements equal to 1.0 × 1 $0^{-9}$ cm³, which corresponds to a computational domain of about 1.1 × 10⁶ elements and provided an appropriate description of the different flow features. The chosen value for the mesh size is adequate for the LSAs region and in line with available literature data: Mori et al.²⁶ considered a mesh size equal to 0.03 cm, while the minimum volume of the elements used by Liu et al.²⁷ is 1.0 × 10⁻⁸cm³. Sensitivity analysis of the computational domain was performed considering 0.015, 0.017, and 0.019 cm, as global maximum edge sizes and did not lead to significant changes of the numerical solution. Since the chosen mesh size (0.017 cm) is finer than those generally used,^26,27 we limited the sensitivity analysis to $\pm 10\%$ variations. Though over a restricted range of values, the sensitivity analysis is comforting. (Details are offered in the supplementary material.) Based on this, we adopted the intermediate (0.017 cm) and not the finest mesh size, considering that changes are minimal but computational times are more affordable.

C. AF features through 0D cardiovascular-cerebral modeling

We here recall the main features of the computational algorithm [see Fig. 1(c)] combining (i) a stochastic extraction of the heart beating in SR and AF from suitable heart rate-specific probability density functions with (ii) a cardiovascular-cerebral lumped parameter model. The ICA flow rate resulting from the 0D cerebral submodel was then exploited as the inlet boundary condition for the above described 3D model. More details can be found elsewhere,¹⁶ while the middle panel of Fig. 1(c) displays a schematic representation of the 0D cardiovascular-cerebral modeling.

1. Beating extraction

The heart beating, RR (s), is defined as the temporal interval between two consecutive heart beats, while the heart rate HR (bpm) is the number of heart beats per minute. For both SR and AF conditions, artificially built RR intervals were built for HR = 50, 70, 90, 110, and 130 bpm.¹⁶ In brief, SR beating was extracted from a correlated Gaussian distribution centered at the considered mean HR and having a constant coefficient of variation, cv = 0.07, for all the HRs. AF beating was extracted from an uncorrelated exponentially modified Gaussian distribution again centered at the chosen mean HR and with cv = 0.24 for all the HRs.^44,45 The so-built RR extraction intrinsically accounts for the increased RR interval variability that occurs during AF. After being tested and validated over clinically measured data,^44,46,47 the resulting RR intervals represent suitable and reliable RR time-series to model SR and AF conditions. 5000 cardiac beats were extracted for each configuration to achieve statistically significant results. The RR probability density distributions [p(RR)] in SR and AF conditions are displayed for the two extreme values of HR, 50 and 130 bpm, in Fig. 1(c).

2. 0D cardiovascular-cerebral model

After RR extraction, the zero-dimensional cardiovascular-cerebral model was run to obtain ICA flow rate time-series, $Q_{\mathit{ICA}}(t)$, corresponding to the extracted RR beating. Through a suitable combination of electrical/hydraulic components (i.e., resistances, compliances, inertances), the 0D cardiovascular submodel describes the arterial and venous circuits of both systemic and pulmonary circulations together with an active representation of the four cardiac chambers. The short-term baroregulation, accounting for the inotropic effects of both ventricles and the control of the systemic vasculature (peripheral arterial resistances, unstressed volume of the venous system, and venous compliance), is also included. Both atria are imposed as passive to simulate the absence of atrial kick during AF, while they can actively contract during SR. The 0D cerebral submodel consists of a network of time-varying resistances and compliances describing the cerebral circulation from the large proximal arteries up to the distal and capillary/venous regions, along with the cerebrovascular control mechanisms of autoregulation and CO₂ reactivity. Both submodels have been validated^13,44 and extensively used to investigate AF effects on the systemic^45,48–50 and cerebral^14–16 circulation. Key features of the 0D cardiovascular-cerebral model are sketched in Fig. 1(c), together with the resulting portions of the ICA flow rate time series in SR and AF (HR = 50 and 130 bpm).

D. Modeling rhythm and rate effects of AF beating

The computational cost of the 3D simulation of the flow field over one cardiac beat (taking about 30 h on a machine with an Intel^® Core^™ i7–4790, CPU 3.60 GHz, 4 cores, 32 GB RAM) makes the 3D simulation along the whole 5000 beats-long ICA time series unfeasible. For this reason, we pursued a different strategy by separately accounting for heart rhythm (case A) and rate (case B) effects, which jointly characterize AF beating.

1. Heart rhythm effects (case A)

The conceptual workflow to build the inlet condition and related outcomes consists of four steps and relies on the negligible role of temporal fluid dynamics inertia in the rigid 3D model. To this aim, we compared numerical simulations when $Q_{\mathit{ICA}}(t)$ evolves according to the typical (time-dependent) hemodynamic tracing against simulations forced by steady ICA discharges, Q_s. In particular, we compared the flow field and WSS patterns at homologous discharge values [i.e., when $Q_{\mathit{ICA}}(t)=Q_s$]. We observed that differences between unsteady and steady cases emerged only during strong flow acceleration or deceleration phases (i.e., |d $Q_{\mathit{ICA}}(t$)/dt| $\gg$ 0), while differences were negligible close to discharge extreme values, that is when $Q_{\mathit{ICA}}(t)$ reaches its maximum values Q_max. (Details can be found in the supplementary material.)

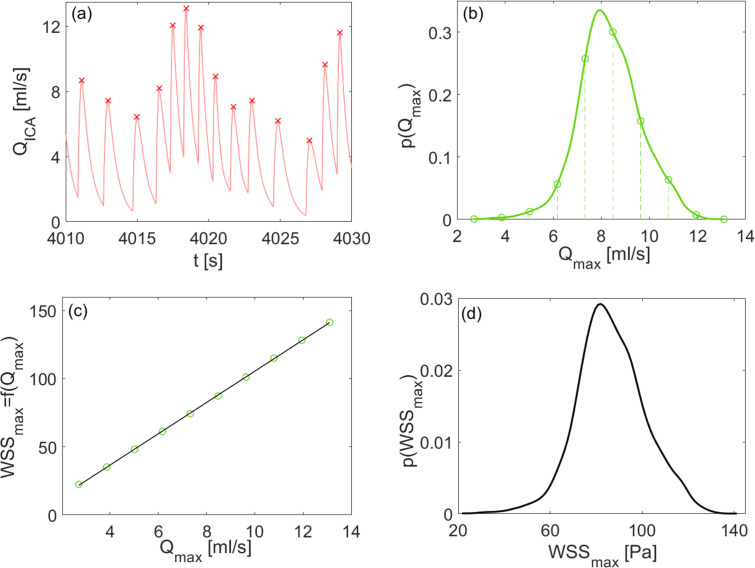
Given these premises, the following four-steps workflow was implemented for each HR (50, 70, 90, 110, 130 bpm) and SR/AF condition and sketched in Fig. 2 (for the AF case at 50 bpm):

• (i)by considering the $Q_{\mathit{ICA}}(t)$ time-series, maximum values, Q_max, over the 5000 beats simulated through the 0D cardiovascular-cerebral model were detected [see Fig. 2(a)];
• (ii)the probability density function, $p(Q_{\text{max}})$, of the Q_max beat-to-beat maximum discharges (5000 values) was extracted [see Fig. 2(b)]. $p(Q_{\text{max}})$ was sampled with ten equally spaced points [green symbols in panels 2(b) and 2(c)] from the minimum to the maximum values. For each of these Q_max values, a steady flow rate simulation was run;
• (iii)since 3D model outcomes are independent from the ICA discharge time history close to Q_max, based on the ten steady flow rate simulations, we built a relationship between the ICA Q_max values and a number of fluid dynamics metrics m (e.g., maximum WSS in the MCA or in a specific LSA) through a one-to-one function such as $m=f(Q_{\text{max}})$ [see Fig. 2(c), where m is taken as the maximum WSS, WSS_max, in the 3D model];
• (iv)
  the probability distribution for the metric m was obtained as the derived distribution from $p(Q_{\text{max}})$, according to the rule

  $$p(m)=\frac{\mathrm{d}{Q}_{\text{max}}}{\mathrm{d}m}p(Q_{\text{max}})=\frac{\mathrm{d}{Q}_{\text{max}}}{\mathrm{d}f(Q_{\text{max}})}p(Q_{\text{max}}),$$ (5)

  where the previously obtained relations $m=f(Q_{\text{max}})$ were exploited, see Fig. 2(d), where $m=WS{S}_{\text{max}}$.

FIG. 2.

Conceptual workflow to account for heart rhythm effects (case A), AF condition at 50 bpm: (a) representative Q_ICA time-series where maximum values, Q_max, are evidenced by red symbols; (b) probability density function, $p(Q_{\text{max}})$. Vertical dashed lines and related green symbols highlight the ten equally spaced discharge values chosen and simulated in steady state conditions to build the relation $f(Q_{\text{max}})$; (c) function $m=f(Q_{\text{max}})$ with m taken as the maximum WSS, WSS_max, in the 3D model (green symbols show the ten flow rate values chosen and the corresponding m values resulting from the ten steady state simulations); (d) derived distribution p(m), here $m=WS{S}_{\text{max}}$.

This workflow was adopted for SR and AF conditions at the considered HRs, obtaining ten pdfs p(m) representing the probability distributions of the metric m at the maximum values of the ICA flow rate for five mean HRs (50, 70, 90, 110, 130 bpm) both in sinus and fibrillated rhythm. In particular, for the m metric, we focused on discharges flowing in the MCA and LSAs, and wall shear stress averaged on the N pixels ranked with the highest WSS. (This metric was studied separately for the MCA and LSAs.) Sensitivity analyses showed that N = 50 in the MCA and N = 20 in the LSAs represented the optimal choice highlighting high WSS values and avoiding very local spurious WSS spikes.

2. Heart rate effects (case B)

Inlet condition is conceptually simpler since a single periodic pulsatile flow rate waveform, $Q_{\mathit{ICA}}(t)$, at the considered HR (50, 70, 90, 110, 130 bpm) was imposed. Outcomes were obtained directly from the numerical simulation of the 3D model for a single beat.

III. RESULTS

The results are first shown accounting for the heart rhythm effects (case A), thus highlighting AF variability at different HRs, in terms of MCA/LSAs flow rates and derived distributions, p(m), for WSS_max and LSA flow rates, Q. Then, heart rate effects (case B) will be displayed through 3D maps reporting beat-averaged and differential WSS values as well as FV streamlines for the periodic beating at 50, 70 (baseline), and 130 bpm. For both cases A and B, the LSAs region will be zoomed and separately focused on. Other hemodynamic indexes, such as the oscillatory shear index and the endothelial cell activation potential, accounting for the emergence of reversed flow, have been computed but turned out to be scarcely significant due to reduced oscillatory nature of the ICA to LSAs flow dynamics. Wall shear stress gradient was evaluated as well but did not bring any more significant information than already highlighted by the beat-averaged WSS. Therefore, we here do not show the oscillatory shear index, the endothelial cell activation potential, and the wall shear stress gradient results, but we focus on the most significant hemodynamic markers, that is WSS and FV related parameters.

A. Role of heart rhythm

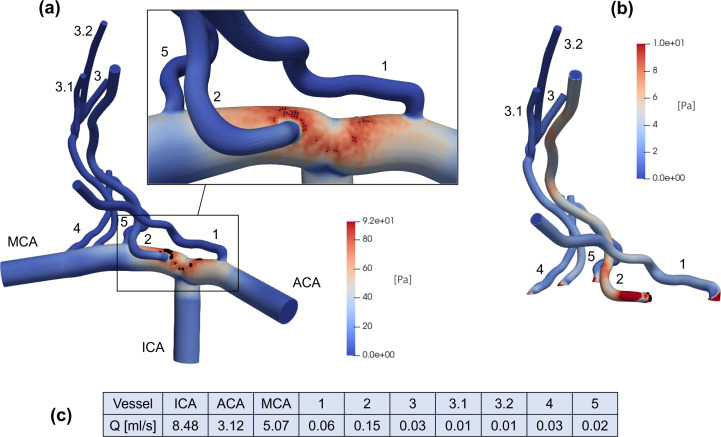
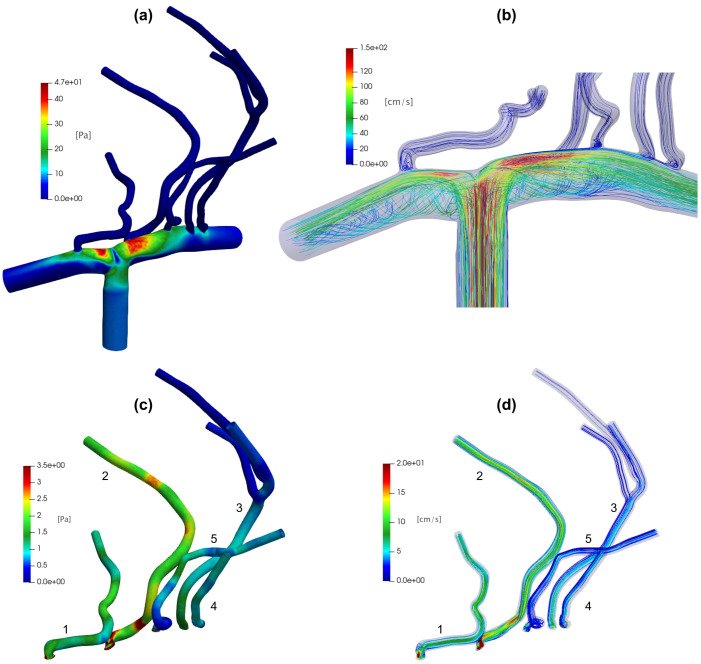
Figure 3 shows, for an intermediate $Q_{\mathit{ICA},\text{max}}$ value (8.48 ml/s) used as constant ICA inlet for the 3D model, the resulting WSS map [panel (a)] and discharge values in different domain regions [panel (c)]. Panel (a) also displays the N = 50 pixels (marked as black dots) which, when averaged, determine $m=WS{S}_{\text{max}}$ corresponding to the selected value $Q_{\mathit{ICA},\text{max}}=8.48\hspace{0.17em}\text{ml}/\mathrm{s}$ (used as inlet condition). Maximum values are reached in the region where the ICA bifurcates into the ACA and MCA [see also the zoomed inset of panel (a)], which holds true also for other constant inlet values in the range^2,14 ml/s. In panel (b), WSS is shown for LSAs alone, together with the N = 20 pixels (marked with black dots) defining $m=WS{S}_{\text{max}}$ for the LSAs region only. The maximum values are reached at the entrance of LSA 2 (the first LSA departing from the MCA) and remain still high along the entire length, a feature which again is true for other constant Q_max values. The range of WSS values reached in the LSAs ([0, 10] Pa) is comparable with the CFD analyses obtained with standard values of pulsatile flow rate in the case of infarct in non-LSA territory.²⁶ In panel (c), steady state flow rate values are reported. Blood flow is mainly distributed in LSAs 1 and 2; in particular, LSA 2 is the one with the greatest discharge (0.15 ml/s).

FIG. 3.

Representative CFD outcomes with constant ICA inlet (8.48 ml/s): (a) WSS map of the whole 3D model, together with the first N = 50 pixels (marked as black dots) having maximum WSS values (the highest WSS region is zoomed in the inset); (b) WSS map of the LSAs with the N = 20 pixels (marked as black dots and located at the entrance of LSA 2) reaching the maximum WSS values; (c) steady state flow rate values in the different vessels.

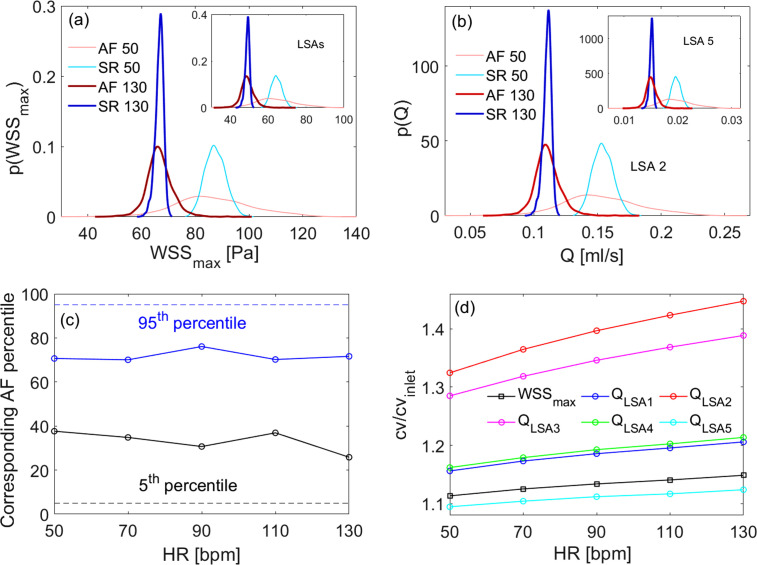
In Fig. 4, derived distributions of maximum wall shear stress, $p(WS{S}_{\text{max}})$ for the whole 3D model [panel (a)] and the LSAs region alone [inset panel (a)], and flow rate, p(Q) in the LSA 2 and LSA 5 [panel (b) and relative inset], are shown for 50 and 130 bpm. The derived distributions are informative of the range of values reached, for each HR and rhythm condition, by the key hemodynamic variables. We note that: (i) WSS_max and flow rate mean values decrease (similarly in SR and AF) as HR increases from 50 to 130 bpm: from 87 to 67 Pa (mean WSS_max of the whole 3D model), from 64 to 49 Pa (mean WSS_max of the LSAs region), from 0.15 to 0.11 ml/s (mean $Q_{\mathit{LSA}2}$), and from 0.02 to 0.015 ml/s (mean $Q_{\mathit{LSA}5}$); (ii) at all HRs, AF induces a much higher variability compared to SR (at the same HR).

FIG. 4.

Role of heart rhythm through derived distributions, percentile analysis and amplification of variability. (a) Derived distributions $p(WS{S}_{\text{max}})$ for the whole 3D model and in the LSAs region alone (inset), at 50 and 130 bpm. (b) Derived distributions p(Q) in the LSA 2 and LSA 5 (inset) at 50 and 130 bpm, respectively. (c) Evaluation of AF percentiles corresponding to the SR thresholds (fifth and 95th) as a function of HR (dashed lines recall the fifth and 95th reference percentiles in SR). (d) Amplification of variability $cv/c{v}_{\mathit{inlet}}$ during AF in the LSAs for WSS_max and Q.

To quantify the higher AF-induced variability, the analysis of the derived distribution tails reveals whether extreme hemodynamic values that would normally be unlikely in SR may become more often reached in AF. Figure 4(c) displays the AF percentiles corresponding to SR fifth (black bullet curve) and 95th (blue bullet curve) percentiles. (Percentile analysis is representative of WSS and Q variables, as derived distributions have very similar shape for all the hemodynamic variables here considered.) The AF value corresponding to the 95th percentile during SR sets around the 70th, while the value corresponding to the fifth percentile SR is around the 30th in AF, in both cases not showing significant trends with HR. It follows that in AF there are extremely high/low values much more probable than in SR, and this higher probability remains almost constant for all the considered HRs.

Finally, although the hemodynamic variability decreases with HR (that is, $cv=\sigma /\mu$ values of all the hemodynamic variables considered decrease with HR, as also observed in Ref. 16), this does not occur uniformly for all the variables and in the different vascular districts. Figure 4(d) shows in AF the $cv/c{v}_{\mathit{inlet}}$ ratio as a function of HR for the WSS_max in the LSAs and for the flow rates Q in each LSA (cv_inlet refers to the $Q_{\mathit{ICA},\text{max}}$ inlet distribution). There is an amplification of the variability in the LSAs region with respect to the carotid inlet (all the $cv/c{v}_{\mathit{inlet}}$ ratios are well above 1); furthermore, for both wall shear stress and flow rate, this amplification always increases with HR. Moreover, the amplification of the variability of flow rates is different in various LSAs and does not depend either on the average blood load or the location of the bifurcation: LSA 2 [the first LSA along the MCA encountered after the T-shaped ICA–MCA–ACA bifurcation, red curve in Fig. 4(d)] is the most prone to undergo a greater amplification of the variability; however, the least prone is the LSA 5 [cyan curve in Fig. 4(d)], which is located immediately after LSA2: in terms of amplification of variability, LSA 2 appears to play a protective role against LSA 5.

B. Role of heart rate

We here consider the net heart rate role by showing WSS and FV maps obtained by means of pulsatile ICA flow rate inlet with periodic beating ranging from 50 to 130 bpm. Since the beat-averaged ICA inlet flow rate is maintained constant (4.7 ml/s) at all HRs due to cerebral autoregulation mechanisms implemented in the 0D cardiovascular-cerebral model,¹⁶ WSS and FV maps averaged over the cardiac beat do not change with HR, thus are displayed for the baseline HR of 70 bpm only (Fig. 5).

FIG. 5.

Beat-averaged results with pulsatile ICA flow rate inlet at baseline 70 bpm. Top panels: (a) beat-averaged WSS and (b) FV streamlines for the whole model. Bottom panels: (c) beat-averaged WSS and (d) FV streamlines in the LSAs.

Panels (a) and (b) of Fig. 5 show beat-averaged WSS and FV maps for the whole 3D model, respectively. We here interpret, from a fluid dynamics point of view, the spatial distribution of the beat-averaged WSS by relating it to the most evident flow field features. The vascular regions with the greatest WSS are the upper walls of the MCA and ACA just past the T-shaped bifurcation ICA–MCA–ACA. (The region around the stagnation point has a WSS value close to zero.) The upper walls with elevated WSS involve all the grafts of the LSAs (the farthest LSAs 3 and 4 are a bit less influenced), which, therefore, experience high WSS at their inlets. The lower walls of the ACA and MCA instead reach very low WSS. By observing the beat-averaged flow field [Fig. 5(b)] near the T-shaped bifurcation, there is an abrupt flow deceleration (almost zero WSS and FV values at the stagnation point) and the generation of two separate flow currents: one toward the MCA and the other toward the ACA. Close to the MCA and ACA upper walls, the velocity field reaches the greatest values and is substantially ordered, attached, and parallel to the walls, generating high WSS. Close to the lower MCA and ACA walls, relevant recirculation regions emerge, where the flow is definitely slower, helicoidal, not parallel, and no more attached to the wall. This causes the WSS here to be very low.

A similar picture relating WSS spatial distribution and flow field features, even if less evident due to the lower WSS and FV values, can also be found in the LSAs [Fig. 5, panels (c) and (d)]: to the high WSS values, we, therefore, associate a faster velocity field, which is attached to the walls, aligned with the vessel axis and having ordered streamlines; low WSS values are instead associated with recirculating flow regions, where the velocity field separates from the walls, slows down, and becomes less ordered (that is, more vortical and helicoidal).

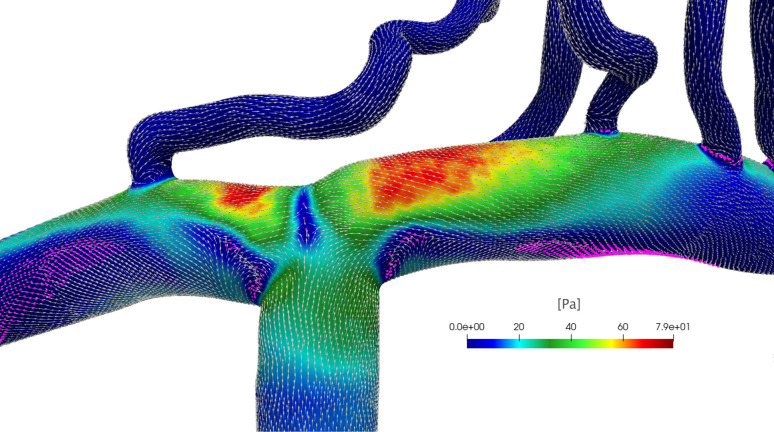
Figure 6 shows the WSS direction (vectors), magnitude (color map), potential WSS fixed points, and manifolds (magenta points) in correspondence of the systolic peak of the pulsatile ICA flow rate at 70 bpm for the ICA–MCA–ACA region. WSS vectors are mainly oriented in the mean flow direction; however, important deviations from this direction are found in proximity of the recirculation and separation regions that are close to the lower walls of the ACA and MCA and T-shaped bifurcation ICA–MCA–ACA, where low WSS magnitude values are reached. Although not easily detectable with simple visualization, WSS fixed points are points on the vessel wall where the WSS vector vanishes and is often used as indicators of the flow topology; in particular, they are associated with upwelling motion and possible flow separation.⁵¹ Also here, indeed, potential WSS fixed points evidence stagnation points (T-shaped bifurcation ICA–MCA–ACA) as well as recirculating flow and separation regions (lower walls of the ACA and MCA), where the WSS direction transversal to the vessel axis is relevant and potentially attracting WSS manifolds linking fixed points emerge. However, the precise detection of these points and manifolds relies on a dynamical system theory and requires rigorous Lagrangian-based and Eulerian-based post-processing techniques.⁵²

FIG. 6.

WSS direction (vectors) and magnitude (color map) at the systolic peak of the pulsatile ICA flow rate for 70 bpm evaluated in the ICA–MCA–ACA vascular region. The WSS vectors are normalized for visualization. Magenta points show potential WSS fixed points and manifolds detected considering points having the WSS magnitude lower than the fifth percentile value of the WSS probability distribution in the ICA–MCA–ACA region.

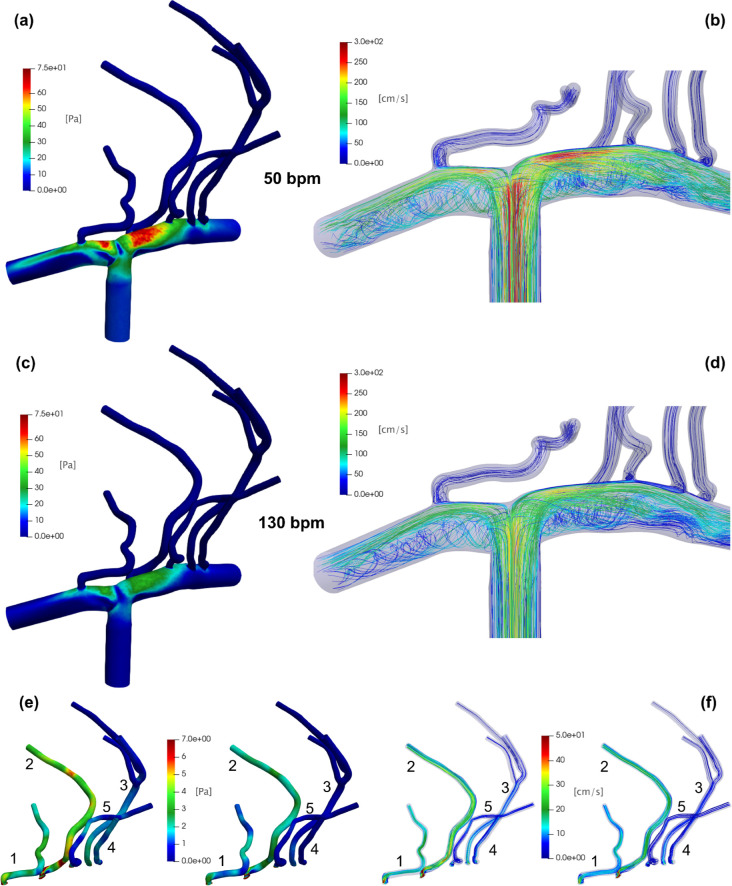
If beat-averaged WSS and FV maps are the same for all HRs, the instantaneous WSS and FV values corresponding to minima and maxima of the Q_ICA inlet change with HR [see a representative example in the right panel of Fig. 1(c)]. In Fig. 7, we report ${\Delta }_{\mathit{WSS}}=\mathit{WSS}(Q_{\mathit{ICA},\text{max}})-\mathit{WSS}(Q_{\mathit{ICA},\text{min}})$, describing the intra-beat shear stress excursion at the wall, and $FV(Q_{\mathit{ICA},\text{max}})$ that is the flow field at the maximum value of Q_ICA, at different HRs. Passing from 50 to 130 bpm, an overall Δ_WSS reduction is observed. In particular, the ACA and MCA upper walls—where beat-averaged WSS is around 45 Pa and constant for all HRs [Fig. 5(a)]—are the most affected regions by the Δ_WSS variation. Here, Δ_WSS decreases from values around 75 Pa at 50 bpm [Fig. 7(a)] to values not exceeding 40 Pa at 130 bpm [Fig. 7(c)]. At the lower walls, where beat-averaged WSS is instead lower, less significant Δ_WSS variations are observed as HR increases from 50 to 130 bpm. In both upper and lower wall regions, increasing HR reduces Δ_WSS excursion, and this is mainly caused by a reduction in the WSS_max values (not shown here). The scenario is confirmed when looking at $FV(Q_{\mathit{ICA},\text{max}})$ [Figs. 7(b)–7(d)]: in fact, passing from 50 to 130 bpm, streamlines close to the upper walls are still parallel each other and ordered, but the flow velocity is markedly slowed down. At the same time, at the lower walls, the helicoidal flow structures that are separated from the walls show a reduced velocity field, consequently increasing the residence time of the blood in the recirculation areas.

FIG. 7.

Role of heart rate through WSS and FV instantaneous values at 50 and 130 bpm. Top panels: (a) Δ_WSS and (b) $FV(Q_{\mathit{ICA},\text{max}})$ at 50 bpm. Middle panels: (c) Δ_WSS and (d) $FV(Q_{\mathit{ICA},\text{max}})$ at 130 bpm. Bottom panels: LSAs zoom for (e) Δ_WSS and (f) $FV(Q_{\mathit{ICA},\text{max}})$ [left panels (e) and (f): 50 bpm; right panels (e) and (f): 130 bpm].

With due proportions given the reduced hemodynamic values reached, the resulting picture is similar also for the LSAs [see Figs. 7(e) and 7(f)]. In particular, perforating arteries appearing the most prone to decreases of Δ_WSS and $FV(Q_{\mathit{ICA},\text{max}})$ induced by increasing HR are the first encountered after the T-shaped bifurcation, that is LSAs 1 (along the ACA) and 2 (along the MCA). On the contrary, more downstream LSAs 3, 4, and 5 are less exposed to alterations, maintaining low WSS and FV values at all HRs.

It, therefore, emerges that an increase in HR reduces the spread between $\mathit{WSS}(Q_{\mathit{ICA},\text{max}})$ and $\mathit{WSS}(Q_{\mathit{ICA},\text{min}})$, mostly reducing the $\mathit{WSS}(Q_{\mathit{ICA},\text{max}})$ throughout the vascular domain. The generalized WSS decrease is associated with a significant variation of the FV distribution, and this fluid dynamics correlation has important implications in terms of blood flow patterns: in the higher WSS regions (e.g., the upper walls of the ACA and MCA), the FV slows down but still remains aligned and parallel to the walls, while in the lower WSS regions (e.g., the lower walls of the ACA and MCA), the already present region of helicoidal and separating flow slows down further, favoring the blood stagnation (with consequent possible clot formation) and the potential accumulation of atheromatous plaques.^53–56

IV. DISCUSSION AND CONCLUSIONS

Combining results from cases A and B, we first observed a higher variability of the hemodynamic variables during AF. The percentile analysis quantifies this greater variability by showing that extremely high/low values are much more probable in AF without evidencing any trend with HR. This last is instead observable evaluating the $cv/c{v}_{\mathit{inlet}}$ ratio, which showed an amplification of the variability with HR as well as heterogeneity of the response in the different vascular districts of the LSAs. Both cases A and B highlighted a reduction of WSS_max and Δ_WSS as HR increases. We recall that WSS and related metrics are crucial markers of the endothelial cells function, and they are widely adopted to evaluate the lesional state and the consequent increased risk of thrombogenesis and atherosclerosis onset. In fact, it has been observed that low WSS conditions promote adherence between endothelial and blood cells, favoring thrombogenesis, formation of atherosclerosis and inflammatory states.^53–56 A recent CFD analysis on the LSAs showed that in patients with LSAs infarct, WSS and FV are lower in the ipsilesional LSAs than in the contralesional LSAs: a more pathological response (that is, greater susceptibility to atherogenesis) was, therefore, associated with lower WSS and FV.²⁶ Another CFD study of a single-patient aortic region observed that some features of AF, including the absence of atrial kick and reduced ventricular function, modify the flow structure, reducing the WSS and originating zones of reversed flow, both these last findings suggesting thrombogenesis hazard and the increased possibility of plaque formation in the aortic arch and descending aorta.²¹ In a more recent CFD analysis on different patients, the same group of authors reported that the above mechanisms are exacerbated if AF acts concomitantly with vascular changes due to the ageing.²²

Therefore, our findings about low WSS and FV values in the cerebral hemodynamics during AF might suggest a more risky state. Moreover, through the flow field analysis carried out in case B, we recall from a fluid dynamics point of view why low WSS regions are more susceptible to atherogenesis. Indeed, since the velocity near the wall is related to WSS, low WSS regions correspond to stagnation flow points. In these vascular areas, the flow slows down considerably and where this occurs in the presence of already existing recirculation patterns (MCA and ACA lower walls or inlet of the LSAs) the residence time of the blood and consequently the probability of clot/thrombus formation increase. The low WSS values are much more likely to be achieved at high HRs and if hemodynamic variability is high, both features characterize AF beating.

Finally, focusing on the LSAs, both analyses A and B showed a heterogeneity of the response in the different vascular districts. In particular, both the $cv/c{v}_{\mathit{inlet}}$ ratio and the Δ_WSS analyses displayed that the LSAs most affected by the AF-induced variations are the first departing from the ACA and the MCA, i.e., LSAs 1 and 2, while the subsequent LSAs along the MCA are less exposed to alteration. LSAs are the sole blood supply of basal ganglia and do not have a significant collateral blood supply.^11,57 For this reason, the LSAs are considered end arteries and, therefore, particularly prone to hypoxia. In this regard, it has been observed that intracranial atherosclerosis, either as atheroma of the MCA/ACA or in the LSAs, is the most frequent cause of lacunar strokes, namely, ischemic strokes located in the LSAs.¹² The reduction of WSS and its high variability induced by AF especially for the LSAs 1 and 2 (which are the LSAs providing the greatest blood supply) here highlighted may, therefore, be indicative of a greater atheromatosis hazard and, consequently, a higher AF-induced lacunar stroke risk.

This study has some limiting aspects. First, rigid wall assumption was considered for the CFD analysis by neglecting deformation and compliant effects of the distal cerebral hemodynamics. Second, the parametric analysis was carried out on the vascular morphology of a single subject, while inter-subject variability needs to be explored in future works. In the end, no patient-specific data were exploited as the computational algorithm combining AF stochastic beating extraction with the 0D cardiovascular-cerebral refers to a generic subject.

In conclusion, by combining different AF features, the CFD analysis of the LSAs using high-resolution MRI showed a significant AF-induced change of WSS and FV fields. This study suggests that AF at higher HR leads to a potentially more hazardous hemodynamic scenario at the level of the LSAs. These results highlight the increasing importance of CFD analyses in hemodynamics and how CFD can guide future clinical investigation on the topic.

SUPPLEMENTARY MATERIAL

See the supplementary material for the mesh sensitivity analysis, the role of inertial effects in the proximity of inlet flow rate maximum values, and a test case (namely, the laminar flow in a curved tube), comparing results obtained through Simvascular with different CFD investigations and analytical approximations.

AUTHOR DECLARATIONS

Conflict of Interest

The authors have no conflicts to disclose.

Author Contributions

S. Scarsoglio and A. Saglietto contributed equally to this work.

S. Scarsoglio: Conceptualization (lead); Formal analysis (lead); Methodology (equal); Resources (lead); Software (equal); Supervision (equal); Validation (equal); Writing – original draft (lead); Writing – review & editing (equal). A. Saglietto: Conceptualization (lead); Formal analysis (equal); Resources (equal); Validation (equal); Writing – review & editing (equal). F. Tripoli: Formal analysis (equal); Methodology (equal); Software (lead); Validation (equal); Writing – review & editing (equal). J. J. M. Zwanenburg: Conceptualization (equal); Investigation (equal); Methodology (equal); Resources (lead); Writing – review & editing (equal). G. J. Biessels: Conceptualization (equal); Investigation (equal); Methodology (equal); Resources (lead); Writing – review & editing (equal). G. M. De Ferrari: Conceptualization (equal); Validation (equal); Writing – review & editing (equal). M. Anselmino: Conceptualization (lead); Formal analysis (equal); Resources (equal); Validation (equal); Writing – review & editing (equal). L. Ridolfi: Conceptualization (lead); Formal analysis (lead); Methodology (equal); Resources (lead); Software (equal); Supervision (equal); Validation (equal); Writing – original draft (equal); Writing – review & editing (equal).

DATA AVAILABILITY

The data that support the findings of this study are available from the corresponding author upon reasonable request.