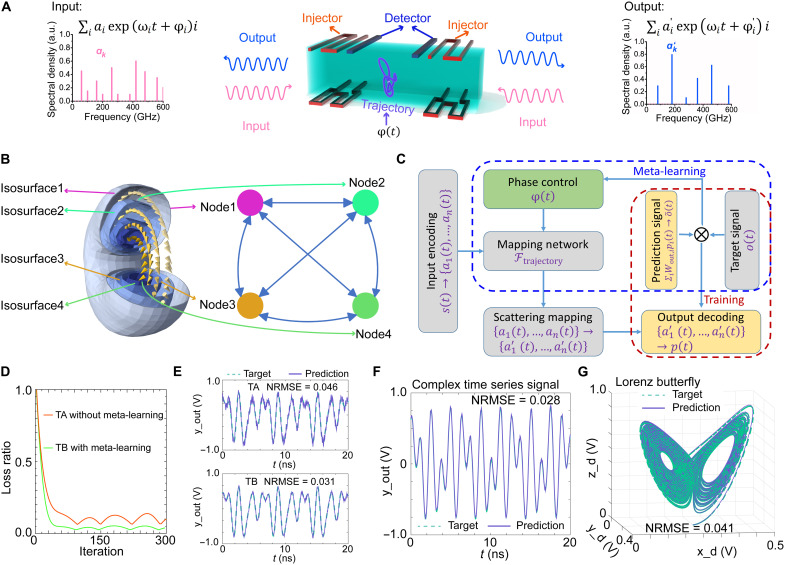
Fig. 6. Meta-learning neural network based on magnon scattering by a hopfion.

(A) Schematic of the meta-learning neuromorphic device. The process of magnon scattering by the hopfion is used to implement the neural network. Carrying the input signal shown in the left frequency spectrum, magnons are injected into the device through the injector antenna. The scattered magnons are received at the detector antenna and are decoded to the right spectrum to obtain the output signal in arbitrary units (a.u.). (B) Correspondence between the neural network nodes and the isosurfaces of the hopfion. The amplitude of magnons of each frequency can be seen as a node in a neural network. The connections between nodes can be treated as the scattering spectrum of magnons. The connections starting from the same node can be seen as an isosurface of the hopfion. (C) Flowchart of the meta-learning framework. The blue dashed circle denotes the meta-learning step, and the red dashed circle denotes the linear regression step. (D) Normalized loss function (loss ratio) convergence curves for the test task. The red line represents the test without meta-learning. The green line represents the test with meta-learning. (E) Prediction result for the test task without and with the multitask training. Normalized root mean square error (NRMSE) is used to estimate the prediction accuracy. (F and G) Our device performs so well in complex time series tasks that the NRMSE reaches 0.028 for (F) the periodic signal and 0.041 for (G) the Lorenz-like chaotic time series.