静息态功能磁共振成像多尺度熵优化及在颞叶癫痫致痫侧定位中的应用

Abstract

熵模型广泛应用在癫痫脑电分析中，但其在静息态功能磁共振成像（rfMRI）中尚存在主观选择计算参数的问题。为此，本文提出多尺度熵模型优化算法，联合有监督机器学习检验优化效果。以致痫侧定位为例，将20位海马硬化标记患者分为左、右侧2组，利用敏感性分析指标优化熵模型参数，以组间优化熵值有显著差异的脑区作为对致痫侧敏感的标记，其熵值为特征向量输入支持向量机分类并验证，获得平均准确率达95%的定侧结果，高于目前水平。研究结果显示，熵模型参数优化算法可较为准确地提取对致痫侧敏感的功能影像学标记，达到客观选择癫痫rfMRI熵模型参数的研究目的，为熵应用于先进技术检测提供了依据。

引言

癫痫是由大脑神经元异常放电引起的中枢神经系统功能异常的慢性疾病，严重影响着患者生活和生命质量，且病变可在大规模脑网络中产生分布效应，导致与原发病灶相连的远端脑区发生代谢功能障碍或者结构改变^[1]。手术治疗是难治性癫痫的首选方法，70%以上的局灶性癫痫患者手术治疗后病情得到缓解，颞叶癫痫（temporal lobe epilepsy，TLE）患者表现出最积极的治疗效果^[2-3]。因此，癫痫致痫侧、致痫灶和癫痫传播路径等定位是术前的重要准备，定侧是基础^[4]。

临床上，对于癫痫疾病诊断以及致痫灶定位常采用脑电图和常规结构磁共振成像（magnetic resonance imaging，MRI）技术。脑电图是临床上定位致痫灶和致痫侧的金标准，其通过监测始发异常神经放电实现定位。然而，颅内电极或立体定位电极的插入会不可避免地造成脑组织损伤，并且脑电存在空间分辨率低、灵敏度不足、观察范围有限和费用昂贵等缺点^[5]。此外，常规MRI作为TLE患者术前定位最常用的检查方法，通过对海马形态的观察和海马体体积测量能够对部分TLE患者作出定位诊断^[6]。海马阳性是致痫侧的典型标识，但只有海马区神经元丢失达50%机体形态才会表现阳性的异常标记^[7]，所以，常规MRI扫描对致痫灶和致痫侧定位诊断的检出率（33%）较低^[8]。

近年来，静息态功能磁共振成像（resting-state functional MRI，rfMRI）以其无损、快捷和广泛的患者适应性等优势，成为检测癫痫引起异常脑功能的先进技术。研究表明，不同致痫侧的TLE患者rfMRI存在较大差异^[9-10]。Barron等^[11]发现不同致痫侧的TLE患者丘脑和颞叶之间功能连接强度存在差异；Yang等^[12]分析TLE患者的静息态功能连接，发现该方法选取的特征量能够较为有效地区分TLE患者的致痫侧。rfMRI不仅可以从脑功能水平揭示疾病脑区病理变化，还能增加手术的安全性和准确性，对神经疾病术后及疗效监测有较大的临床应用价值^[13-15]。

以往，熵模型广泛应用于癫痫脑电信号分析。为从神经信号中提取更多有效信息，Costa等^[16]提出多尺度熵（multi-scale entropy，MSE）模型将熵和尺度联合共同表征生理系统在不同状态下所表现的复杂特性。MSE模型被广泛用于分析具有多尺度和非线性特点的脑电^[17]、fMRI^[18-19]、功能性近红外光谱（functional near-infrared spectroscopy，fNIRS）^[20]和心脑信号^[21-23]。Yang等^[24]通过MSE模型发现年轻人和老年人的血氧水平依赖（blood oxygen level dependent，BOLD）信号复杂度存在差异，Li等^[20]通过MSE模型发现轻度认知障碍患者、阿尔茨海默病患者和健康人的fNIRS信号复杂度也存在差异。然而，MSE模型的参数选择对信号本身存在较大依赖性，以往多依赖经验选取参数，具有一定的主观性。对rfMRI信号来说，常采用m = 1、r = 0.5^[19]或m = 1、r = 0.35^[24]等。

TLE患者rfMRI信号的非线性显著高于健康人^[25-26]，因此，应用MSE模型研究TLE患者的rfMRI复杂度，或可为患者的检测或治疗提供新思路。本文以rfMRI致痫侧定位为例，试图用敏感性分析的接受者操作特征曲线（receiver operating characteristic，ROC）及其曲线下面积AUC值（area under ROC curve，AUC）优化MSE模型的计算参数。为检验优化效果，通过优化后的熵模型提取对致痫侧敏感的功能像标记，并将其熵值作为特征向量输入至可适应小样本的机器学习模型——支持向量机（support vector machine，SVM）定侧，以其精度评估优化有效性，试图解决MSE参数选择依赖经验和数据特征、缺少统一客观依据的计算瓶颈，为熵值应用于TLE患者rfMRI提供客观依据。最后，由于SVM是有监督学习模型，需要在正确标注的样本上运行，所以，本文借助结构像海马阳性提示的致痫侧信息进行有监督的机器学习。整体分析框架如图1所示。

图 1.

Study flowchart

分析流程图

1. 数据与方法

1.1. 数据采集

本文中20名TLE患者rfMRI数据来自南京大学医学院附属金陵医院医学影像科，其中男性9例，女性11例，年龄19～33（25.7±3.7）岁，接受常规的术前评估以定位癫痫放电区域。其中结构像海马阳性左侧和右侧的患者各10例（男性，左侧4例，右侧5例；女性，左侧6例，右侧5例），命名为左侧组和右侧组。

数据采集使用Siemens 3.0T高场强超导MR扫描仪，经单次激发GE-EPI序列采集BOLD-fMRI数据，TR = 2 000 ms，TE = 30 ms，翻转角度为90°，矩阵64×64，扫描视野240 mm×240 mm，层厚4.00 mm，层间距0.40 mm^[27]。本研究获得南京军区总医院医学伦理委员会批准，患者知情并且签署知情同意书。

1.2. 数据预处理

使用FMRIB软件库中的工具进行rfMRI数据预处理^[28-29]，处理流程和质量检测（头动控制量 < 0.2 mm）在美国哈佛医学院Martinos医学影像中心完成^[30-31]。处理平台CPU为Intel Xeon Sliver 4112 × 16，64核，操作系统Centos7.6，每个被试者的数据预处理时间约为15 h。

预处理步骤：① 将每个被试采集的前4个时间点数据移除，使信号更加稳定；② 使用SPM2校正切片采集的每个脑体积时间偏移（Wellcome Department of Cognitive Neurology，London，英国）；③ 利用FSL软件（http://fsl.fmrib.ox.ac.uk/fsl）对头部运动进行刚体平移和旋转^[32]；④ 全脑平均信号的归一化，将信号配准到蒙特利尔神经研究所（Montreal Neurological Institute，MNI）的标准空间，重采样到2 mm各向同性体素大小；⑤ 带通时间滤波（0.01～0.08 Hz）。

预处理后，使用win10操作系统MatlabR2018b版本的DPABI将数据投射到自动解剖标记（the anatomical automatic labeling atlas，AAL1）上，每个被试者的数据处理时间约为20 min，将每个被试全脑分成116个脑区，每个脑区有246个时间点，时间长度为490 s。

1.3. 多尺度熵

1.3.1. 多尺度熵模型

多尺度熵模型通过评估量化生物医学信号的“复杂度”，能够有效分析信号的动态变化，因此在神经信号分析中具有应用价值，特别是癫痫这种动态疾病。

多尺度熵的计算步骤：

1）将采集长度为N的时间序列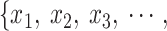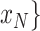进行粗粒化，重新构建一个时间序列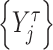如式（1）所示。粗粒化（非重叠式）是根据选取的时间尺度大小，对连续的时间点取平均值，重新构建时间序列。

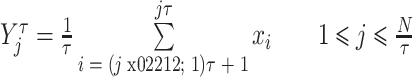1

式中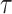为时间尺度。

2）定义多尺度熵模型参数m，其中m为整数，代表比较向量的长度。按顺序构建一组m维矢量，即， 。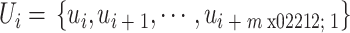

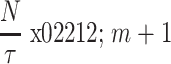3）定义多尺度熵模型参数公差阈值（即相似系数r），其中r为实数，代表匹配阈值。定义U_i与U_j之间的距离 为两个矢量中元素之间距离的最大值，即 ，其中i ≠ j，统计当 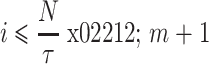时 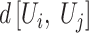小于r时的数目b，并将b与距离总数 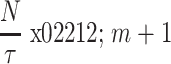的比值，记做 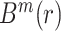，如式（2）所示。

2

4）将维数m加1，在重新设定维度m的情况下重复步骤2、3，将会得到。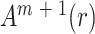

5）理论上，多尺度熵计算如式（3）所示：

3

当N有限时，式（3）的计算模型如式（4）所示：

4

综上所述，多尺度熵中的3个参数分别为维度m、相似度r和时间尺度τ。若计算所得熵值越大，表明复杂度越大，反之亦然。

1.3.2. 熵模型参数优化准侧

多尺度熵是在不同时间尺度值下计算时间序列的样本熵，所以，多尺度熵模型中维度m和相似度r的选取与样本熵参数选取相似。因为多尺度熵的3个参数之间相互影响，则在单个参数优化过程中，其余两个参数也须参与优化过程，即3个参数同时参与一个参数的优化过程。本文中，首先利用组间熵值差异较大（P ≤ 0.05）的脑区数量确定维度m和另外两个参数即将优化的区间，然后，结合ROC曲线和AUC值依次对相似度r和时间尺度 τ 进行优化。多尺度熵模型的参数优化流程见图2。

图 2.

Flowchart of parameters optimization in a multi-scale entropy model

模型参数优化流程图

原则上，熵评估的准确度会随着维度m和m + 1的矢量（时间序列）匹配数量的增加而提高，选择较小的维度m和较大的相似度r也能够增加矢量匹配数量提高准确度。基于时间长度10^m～20^m（m参数维度）的BOLD信号可较为准确地计算熵值^[33]。根据本文中数据的时间点长度可以选取m = 1或2。

根据经验，相似度r范围可选在0.05～0.6。但对文中数据分析发现：在r = 0.05～0.3时，脑区熵值会出现无效值，这是由于选取相似度r较小，计算过程中不存在与之相匹配的矢量。为保证分析精确性，相似度r选在0.3～0.6（步长0.02）范围内，时间尺度也不宜选择过大，本文选取范围是 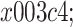= 1～5。

本文用敏感性分析的ROC曲线（反映分类效果敏感性和特异性连续变量的综合指标）和AUC值（ROC曲线下方的面积大小）来评估MSE模型参数的优化，使参数有利于分析癫痫rfMRI信号特征，使得参数选择具有一定的统计特性和客观性。

1.3.3. 对发作侧敏感的脑区

利用MSE模型计算全脑（AAL1）中90个大脑区域的rfMRI信号得到脑区熵值，并通过t检验对比两组患者脑区熵值的差异性，获得脑区P值。在P ≤ 0.05范围内，选取脑区将其作为对致痫侧敏感的功能影像标记，并利用ROC曲线和AUC值（IBM SPSS Statistics21，美国）对标记进行验证。最后用BrainNet Viewer^[34]（http://www.nitrc.org/projects/bnv/）将标记进行可视化。

1.4. 机器学习

1.4.1. 特征向量

在优化参数下，将对致痫侧敏感的脑区熵值作为特征向量，输入到支持向量机中。

1.4.2. 支持向量机

由Vapnik提出的SVM是一种有监督的机器学习方法，以训练误差作为优化问题的约束条件，并以置信范围最小化为优化目标，是一种基于结构风险最小化准则的学习方法，不易受数据维数和样本数量的限制，这为其在小样本中的应用提供了依据^[35-36]。

文中将20名患者的脑区多尺度熵值作为特征向量，按照3∶2比例分成12名训练集和8名测试集，作为机器学习的基本输入信息进行数据归一化。选择径向基函数（radial basis function，RBF）做为核函数，选取比例参数g = 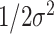代替核参数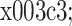，形成一组参数对（C，g）。其中，参数C和g的取值范围设定为［− 10，10］（步长0.2），并用网格搜索方法（交叉验证法）寻找误差最小的惩罚系数C和核参数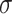为最优参数，创建训练模型，对测试集数据进行计算。

1.4.3. 留一交叉验证

留一交叉验证（leave one out cross-validation，LOOCV）常被用来检测机器学习模型的准确性，其样本利用率较高，能够从有限的样本中尽可能地获取更多有效信息，所以，适用于小样本分析。如果有N个样本，其中N − 1个为训练样本，剩余1个为测试样本，用N次结果的平均分类精度来评估模型的准确性（文中，N = 20）。

2. 结果

2.1. MSE模型的优化参数

调节3个参数（维度m、相似度r和时间尺度τ）计算脑区熵值，通过t检验分析左、右致痫侧TLE患者间的脑区熵值，从而获得具有统计学意义（P ≤ 0.05）的脑区和优化参数范围，并利用ROC曲线和AUC值对其验证。

2.1.1. 维度m优化值

以时间尺度τ = 1～5（步长1）生成图，每张图以相似度r = 0.3～0.6（步长为0.02）为变量，对比维度m = 1和m = 2时组间熵值差异显著的脑区数量来确认维度m优化值，如图3所示。结果发现，m = 1时熵值差异显著的脑区数量明显高于m = 2时（P ≤ 0.05），在τ = 2时，差异较明显，在τ = 3时最为明显，从τ平均角度上看亦如此。很显然，m = 1较m = 2更优，在后面的优化过程中将保持m = 1。另外，在τ = 2～3中，r = 0.54～0.6时熵值差异显著的脑区数量较其他r值要多，即其他2个参数优化将在r = 0.54~0.6、τ = 2～3区间进行。

图 3.

Optimal value of parameter m estimated by number of brain regions with inter-group significant differences in MSE model

以组间熵值差异显著的脑区数量确定维度m优化值

2.1.2. 相似度r优化值

保持维度m = 1时，结合ROC曲线和AUC值对相似度r = 0.54～0.6（步长为0.02）进行优化，如图4所示（τ = 2和τ = 3结果相似，这里只显示了时间尺度τ = 3的结果）。结果发现，当r = 0.54～0.6时，图4a左内侧额上回和图4b右顶上回的ROC曲线都处于参考线以上，说明这两个脑区对致痫侧敏感，可作为标志性脑区。然而图4c左楔叶和图4d左丘脑的ROC曲线在参考线上下浮动，说明这两个脑区不具有分类价值，所以不能作为对致痫侧敏感的脑区。

图 4.

Effects of similarity coefficient r on classification of a single brain area displayed by ROC curves (m = 1, τ = 3)

相似系数r对单个脑区分类效果的ROC曲线(m = 1，τ = 3)

a.左内侧额上回；b.右顶上回；c.左楔叶；d.左丘脑

a. SFGmed.L; b. SPG.R; c. CUN.L; d. THA.L

这个规律也可通过脑区AUC值体现（τ = 2和τ = 3结果相似，这里只给出了时间尺度τ = 3的结果），如表1所示。结果发现，由ROC曲线确认的标志性脑区左内侧额上回和右顶上回，其AUC值也较大，且在r = 0.56时值最大，而左楔叶和左丘脑并不存在合适的r值使其AUC值较大。综上所述，r = 0.56为r的优化值。

表 1. AUC value of classification of a single brain region by different similarity factor r.

不同相似度r下单个脑区侧别分类效果的AUC值

相似度r	左内侧额上回	右顶上回	左楔叶	左丘脑
r = 0.54	0.92	0.89	0.53	0.65
r = 0.56	0.93	0.90	0.53	0.69
r = 0.58	0.89	0.86	0.50	0.56
r = 0.60	0.89	0.90	0.54	0.61

2.1.3. 时间尺度τ优化值

保持m = 1、r = 0.56下，结合ROC曲线和AUC值对时间尺度 τ = 1～5进行优化，如图5和表2所示。结果发现，图5a左脑岛和图5b左中央沟盖在时间尺度因子 τ = 1～5范围内，其ROC曲线多数在参考线之上，说明该脑区可作为对致痫侧敏感的脑区。然而，图5c左楔叶和图5d右背外侧额上回的ROC曲线在参考线上下浮动，不具备分类价值，所以不能作为对致痫侧敏感的脑区。

图 5.

Effects of scale factor τ on classification of a single brain area displayed by ROC curves (m = 1, r = 0.56)

时间尺度因子τ对单个脑区分类效果的ROC曲线（m = 1，r = 0.56）

a.左脑岛；b.左中央沟盖；c.左楔叶；d.右背外侧额上回

a. INS.L; b. ROL.L; c. CUN.L; d. SFGdor.R

表 2. AUC value of classification of a single brain region by different scale factor τ.

不同时间尺度τ下单个脑区侧别分类的AUC值

时间尺度τ	左脑岛	左中央沟盖	左楔叶	右背外侧额上回
τ = 1	0.43	0.46	0.43	0.38
τ = 2	0.72	0.84	0.63	0.55
τ = 3	0.83	0.91	0.53	0.54
τ = 4	0.45	0.67	0.47	0.40
τ = 5	0.62	0.65	0.41	0.59

表2给出单个脑区侧别分类的AUC值，与ROC曲线规律一致。左脑岛和左中央沟盖在τ = 3时AUC值达到最大，而左楔叶和右背外侧额上回则不存在合适的 τ使其AUC值较大。综上所述，τ = 3为 τ的优化值。

综上所述，得到TLE患者rfMRI信号多尺度熵模型的优化参数：维度m = 1，相似度r = 0.56，时间尺度 τ = 3。

2.2. 特征向量

在优化参数（m = 1，r = 0.56，τ = 3）下，计算TLE患者全脑熵值，通过t检验获得P值（P < 0.01），共选出9个标志性脑区，即左中央沟盖、右中央沟盖、左内侧额上回、左脑岛、右脑岛、右顶上回、左楔前叶、右尾状核、右颞极：颞上回。各脑区ROC曲线及脑区在皮层表面的投影如图6所示。

图 6.

Bio-marker brain regions

标志性脑区

a.在多尺度熵模型优化参数（即m = 1，r = 0.56，τ = 3）下9个标志性脑区的ROC曲线；b. 9个标志性脑区的三视图

a. ROC curves of 9 bio-marker brain regions at optimized parameters (m = 1, r = 0.56, τ = 3) in MSE model; b. three-views of 9 bio-marker brain regions

将以上脑区AUC值和P值列入表3，可以看出标志性脑区AUC值较大，并且其P值皆小于0.05。

表 3. AUC value and significance (P value) in a bio-marker area.

标志性脑区的AUC值和统计值

标志性脑区	AUC	P值
左内侧额上回	0.93	0.000 5
左中央沟盖	0.91	0.000 1
右中央沟盖	0.90	0.001 0
右颞极：颞上回	0.90	0.000 7
右顶上回	0.89	0.002 7
右脑岛	0.88	0.002 9
左楔前叶	0.84	0.007 5
左脑岛	0.83	0.001 9
右尾状核	0.82	0.008 1

最后，9个标志性脑区在 τ = 1～5时的组间多尺度熵值变化如图7所示。从图中看出在 τ = 3时，脑区的组间熵值都表现出最大差异，也验证了 τ = 3为优化值。

图 7.

Inter-group MSE values change of 9 bio-marker brain regions

9个标志性脑区的组间多尺度熵值变化

a.左中央沟盖；b.右中央沟盖；c.左内侧额上回；d.左脑岛；e.右脑岛；f.右顶上回；g.左楔前叶；h.右尾状核；i.右颞极：颞上回

a. ROL.L; b. ROL.R; c. SFGmed.L; d. INS.L; e. INS.R; f. SPG.R; g. PCUN.L; h. CAU.R; i. TPOsup.R

2.3. SVM分类效果

将9个标志性脑区的优化熵值作为特征向量，按照3∶2比例将数据随机分为两组数据，输入到SVM进行定侧，并用LOOCV进一步验证，观察其定侧准确度。

经过20次随机分组计算，定侧精度如表4所示，表中精度（s）为：（92.% ± 7.29）%。留一交叉验证法的定侧结果如表5所示，平均精度为95%。从表4、5中发现，利用优化MSE模型对TLE患者定侧精度较为理想。

表 4. Classification rate (CR) of side classification by random validation (%).

随机分组的分类精度（%）

次数	CR		次数	CR
1	87.5		11	87.5
2	100		12	87.5
3	100		13	100
4	87.5		14	87.5
5	100		15	87.5
6	75		16	100
7	87.5		17	100
8	87.5		18	100
9	87.5		19	87.5
10	100		20	100

表 5. Classification result by LOOCV.

LOOCV的分类结果

编号	1	2	3	4	5	6	7	8	9	10
注：L为致痫侧在左侧、R为致痫侧在右侧
实际类别	L	L	L	L	L	L	R	R	R	R
预测类别	L	L	L	L	L	L	R	R	R	R
编号	11	12	13	14	15	16	17	18	19	20
实际类别	R	R	R	R	R	R	L	L	L	L
预测编号	L	R	R	R	R	R	L	L	L	L

3. 讨论

为进一步体现优化熵模型对区分TLE患者致痫侧的有效性，我们在本文中相同TLE患者数据上计算了由Pearson相关系数表达的传统功能连接（记成FC），由本文采用的敏感性分析（即ROC曲线和AUC值）获得8个组间差异显著脑区的FC为特征向量，并结合SVM进行10次随机交叉验证，分类结果如表6所示，其分类准确度（s）为（68.75 ± 12.81）%。与熵模型相比，FC的分类准确度波动范围较大即稳定性较差，不如本文提出的优化熵模型的分类效果。

表 6. Classification accuracy in machine learning of SVM by FC.

基于皮尔森相关性的SVM机器学习分类精度

验证序号	1	2	3	4	5	6	7	8	9	10
准确率	87.5%	62.5%	75.0%	50.0%	62.5%	75.0%	87.5%	75.0%	62.5%	50.0%

表7^{[9,11-12,37-39]}是本文研究方法与其他方法对TLE患者致痫侧的分类效果对比。从中可以看出熵模型优化方法有助于分析rfMRI数据，为TLE患者定侧研究提供了一种新方法。

表 7. Comparison of classification rate by this work and other studies in localizing epileptogenic hemisphere.

本文与其他分析方法定侧准确率对比

作者	数据	LTLE	RTLE	分析方法	准确率
注：LTLE表示左致痫侧TLE患者，RTLE表示右致痫侧TLE患者，SPECT为单光子发射计算机断层成像技术，FDG-PET为氟脱氧葡萄糖正电子发射计算机断层扫描技术，FLAIR为磁共振成像液体衰减反转恢复序列
Jafari-Khouzani等[37]	SPECT	30	16	图像分割和线性分类器	91%
Kerr等[9]	FDG-PET	39	34	互信息和计算机辅助诊断	89%
Yang等[12]	rfMRI	7	5	静息态功能连接和SVM	83.3%
Barron等[11]	rfMRI	12	12	静息态功能连接和判别分析法	83%
Jin等[38]	MEG	23	23	静息态功能连接和SVM	76.2%
Beheshti等[39]	FLAIR	23	19	SVM	76.19%
本文	rfMRI	10	10	MSE和SVM	95%

目前比较明确的TLE患者病灶包含岛叶、双侧扣带回和楔前叶^[12,38-40]。通过分析TLE患者BOLD信号的变化以及对静息态脑功能网络的影响，发现楔前叶、左右额叶和顶叶中的BOLD信号显著减少，听觉网络中的脑岛及颞上回的功能连接强度降低。此外，还发现TLE患者背侧注意网络中的顶上叶表现出的功能连接强度存在差异^[41-42]。利用基于体素的形态测量法分析不同发作侧TLE患者的结构像，发现颞叶、额叶和枕叶区域的皮质厚度发生变化。通过容积磁共振成像技术对TLE患者和健康对照组的海马不对称性分析得到94%的分类准确度^[43]，但TLE患者的结构像变化不局限于海马体，可能会延伸到颞叶周围的皮质区域和皮质下结构^[44-45]。这些研究结果为本文的标志性脑区提供了支撑。

尽管文中表明优化的多尺度熵模型可较为有效地提取对TLE患者致痫侧敏感的功能影像学标记，为优化多尺度熵模型的参数选择提供了一定的参考性。但无法确定本文所选参数是否适用于不同时间长度的癫痫脑部rfMRI信号，还需要借助其他癫痫脑部rfMRI数据集验证。文中进行机器学习分类的样本量较少，虽获得较为理想的分类准确率，但仍可能存在泛化能力不足的问题。目前无法确定多尺度熵模型结合机器学习在充足样本中能否取得更好的分类效果，需要在此基础上进一步搜集数据深入研究。

4. 结论

多尺度熵模型应用于TLE患者rfMRI，其首要问题是如何客观选择模型的计算参数。为此，以定位致痫侧为例，论文提出借助敏感性分析的ROC曲线和AUC值对多尺度熵模型参数进行优化，使其选择具有一定的客观性。为检验优化效果，用优化参数的熵模型寻求对致痫侧敏感的标志性脑区，以其熵值构成特征向量输入支持向量机进行定侧，获得了较高准确率。分析结果发现9个标志性脑区，即左中央沟盖、右中央沟盖、左内侧额上回、左脑岛、右脑岛、右顶上回、左楔前叶、右尾状核、右颞极：颞上回。将脑区熵值作为特征向量对致痫侧不同的TLE患者的分类准确率可达到95%，说明优化多尺度熵模型能够较为有效地区分TLE患者致痫侧。

利益冲突声明：本文全体作者均声明不存在利益冲突。

Funding Statement

国家自然科学基金资助项目（81871345）；河北省自然科学基金资助项目（E2019202019）

The National Natural Science Foundation of China]