基于定向传递函数的癫痫因效性脑网络动态分析

Abstract

癫痫是一种脑网络连接失调的神经系统疾病，从有向功能连通性的角度分析癫痫发作过程的脑网络机制具有重要的研究价值。本文首先对不同频段的癫痫脑电信号在发作间期、发作前期和发作期以定向传递函数方法构建因效性脑网络，并分析在不同状态下脑网络信息传递的途径及动态变化过程，最后对癫痫脑网络的特征属性的动态变化进行分析。结果表明，从发作间期到发作期癫痫脑网络的拓扑结构由趋向随机网络转变成趋向规则网络，整个脑网络的节点连接呈现出逐渐下降的趋势，但是在额区、颞区、枕区的内部节点之间的通路连接数增加，在病灶区域存在大量信息流出的枢纽节点。α波、β波和γ波的发作期全局效率明显高于发作间期和发作前期，聚类系数变化趋势表现为发作前期大于发作期，发作期大于发作间期，其中额区、颞区、顶叶区的聚类系数明显增加。本文的研究结果说明，对癫痫因效性脑网络的拓扑结构和特征参数的动态分析可以构建出癫痫发作全过程的动态变化模型，今后在癫痫病灶的定位和癫痫发作预测方面具有重要的研究价值。

引言

癫痫是一种脑部神经元异常放电引起大脑功能障碍的慢性中枢系统疾病，癫痫的突然和反复发作给患者及其家庭成员带来极大的痛苦。癫痫的发作过程包括癫痫发作间期、发作前期和发作期，对发作前期和发作期的识别可以分别实现癫痫发作预测和癫痫信号检测。人脑是自然界中最复杂的网络之一，人脑的大量神经元相互连接形成了一个巨大的脑网络，通过这些连接模式产生了人的各种行为和认知功能^[1]。对不同生理状态下的脑网络进行深入地研究可以了解不同脑区之间的相互作用，从而揭示大脑信息流的传递方式，为分析各种脑部疾病及脑认知过程提供理论基础^[2]。2010年国际抗癫痫联盟分类标准认为癫痫是一种脑网络连接失调的疾病，并提出了癫痫脑网络的概念^[3]。从脑网络层次阐述大脑结构、功能与行为的关系，为寻找神经系统疾病的病理和治疗方案提供了一个新思路^[4]。

根据脑网络边的构造方式，可以把脑网络分为以下三种：结构性脑网络，一般是通过磁共振成像（magnetic resonance imaging，MRI）和弥散张量成像（diffusion tensor imaging，DTI）构建；功能性脑网络，是由功能MRI（functional MRI，fMRI ）或脑电图（electroencephalogram，EEG）数据的时序信号而构建^[5]；因效性脑网络，在功能性脑网络基础上，如果连接边是有向的，则称为因效连接网络^[6]。胡云奉^[7]考察了3种不同的脑功能连接计算方法对大脑网络拓扑性质的影响，发现虽然基于不同连接定义构建的功能网络都具有稳定的“小世界”属性，但网络参数差异显著，说明不同的网络连接定义方式对网络拓扑性质存在着广泛的影响。功能性脑网络没有考虑节点之间的因果关系，而因效性脑网络能表示各网络节点之间相关性和信息传递方向性，对揭示癫痫发作机制起到了至关重要的作用^[8]。在构建因效性脑网络时，常用的方法有格兰杰因果分析（Granger causality，GC）、定向传递函数（directed transfer function，DTF）和偏定向相干（partial directed coherence，PDC）等^[9]。李亚兵等^[10]利用动态PDC算法对运动想象EEG信号进行因效性脑网络分析，探讨不同任务脑区间信息流的变化。DTF是在GC的基础上改进而来，是用来定量地分析频域脑网络因果连接特性的重要方法，在脑网络的研究中得到广泛应用^[11]。Wang等^[12]利用DTF方法构建癫痫的因效性网络，并结合卷积神经网络实现癫痫发作预测。Kotiuchyi等^[8]应用DTF和独立成分分析（independent components analysis，ICA）构建癫痫EEG因效性脑网络，对大脑信息的动态活动进行分析，但是该研究缺乏时间和空间维度的关于脑活动信息传递的分析。Hejazi等^[13]应用DTF和GC实现基于颅内EEG信号因效性脑网络的癫痫发作预测，但颅内EEG信号的采集是有创的，导致该研究在临床应用受到局限。

目前，对于癫痫患者在不同状态下脑网络的特征和脑区之间瞬时信息流传递的研究还处于初期阶段，有待进一步地深入研究。如果能够在癫痫患者脑网络的动态变化上有所发现，对癫痫EEG信号检测、癫痫发作预测和癫痫病灶定位都有重要的意义。本文首先利用DTF方法对癫痫患者的 EEG 信号构建因效性脑网络，并从频率、状态和空间三个维度分析癫痫患者在癫痫发作间期、发作前期和发作期不同频段的脑网络信息传递的途径及动态变化过程；然后求出患者在三种不同状态下不同频段脑网络的特征属性（全局效率和聚类系数），同时利用秩和检验对患者的网络特征属性进行统计学检验分析，保留差异具有统计学意义的特征，从而得到一个基于 DTF 方法的癫痫脑网络的动态分析模型。本文的研究成果，可反映癫痫发作的动态变化过程，在癫痫病灶的定位和癫痫发作预测方面或将具有重要的研究价值。

1. 实验数据

本文数据来源为可公开获取的意大利锡耶纳大学头皮EEG数据库(Siena scalp EEG database，SSED)(网址：https://physionet.org/content/siena-scalp-eeg/1.0.0/)，本文已得到授权可以使用该数据库内数据。该数据库由锡耶纳大学神经病学和神经生理学部门采集的14 名癫痫患者的 EEG数据记录组成，其中包括 8 名男性（25～71岁）和 6名女性（20～58岁）。受试者使用采样率为512 Hz的动态视频EEG信号进行监测，电极排列遵循国际10-20系统规则。根据国际抗癫痫联盟的标准，由临床医生仔细核对每位癫痫患者的临床和电生理数据后进行癫痫诊断和癫痫发作的分类。记录数据中包含了每位癫痫患者各10次癫痫发作前后的 EEG 信号。本文提取并分析癫痫患者发作间期、发作前期和发作期三种状态的脑网络特征。每段记录里选取医学专家标记的癫痫发作起始点前 60 s数据作为癫痫发作前期数据，在癫痫发作前50 min 选取 60 s 作为癫痫发作间期数据，最终获得癫痫发作间期和发作前期数据各47段，以保证样本量均衡。

2. 方法

本文的数据处理过程如图1所示，包括三个部分：癫痫EEG信号预处理、癫痫因效性脑网络的构建与动态分析、癫痫脑网络的特征参数分析。首先对癫痫EEG信号进行预处理，去除噪声和数据分段；其次利用DTF构建癫痫因效性脑网络，并且从频率、状态和空间三个维度对其进行动态分析；最后基于图论的方法对癫痫脑网络的聚类系数和全局效率的变化进行动态分析。

图 1.

Data processing flow chart

数据处理流程图

2.1. 数据预处理

有研究表明，EEG信号仅在1~80 Hz频带范围内包含有效信息，故先对所有癫痫患者的EEG数据进行1~80 Hz的带通滤波处理，并对其做50 Hz的陷波处理以消除工频干扰，去除 EEG 信号中的心电，眼动、肌电以及头动信号。如图1所示利用ICA方法将19个通道（Fp1、F3、C3、O1、P3、F7、T3、T5、Fz、Cz、Pz、Fp2、F4、C4、P4、O2、F8、T4、T6）的EEG信号分离成15个独立的信号源，再将心电、眼动等信号从信号源中剔除，对信号源进行重构就能得到19个通道的EEG信号。再利用覆盖率为50%的长度为5 s的滑动时间窗对每一段60 s的数据进行分割，则每个患者单次发作记录得到5 s的发作间期数据和发作前期数据各23段。

2.2. 癫痫因效性脑网络的构建方法

DTF方法是由GC衍生出的一种能表示多个变量在时序上的有向连接的谱方法。它以多元向量自回归（multivariate vector auto regression，MVAR）为框架，表示时序数据的内部不同维度的数据之间存在的依赖关系，并以矩阵形式表现出来。

其中t为时间，Y(t)为时间序列，U(t)为噪声矩阵，A_k表示系数矩阵，k为不同的阶数，k的取值范围[1，p]，序列的多元过程表示成阶数为p的静态、稳定自回归过程，如式(1)所示：

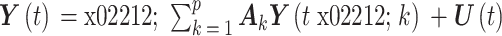1

对式(1)进行频域转换得如式(2)所示：

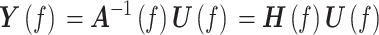2

其中，Y(f)是Y(t)的傅里叶变换，U(f)是U(t)的傅里叶变换。因此可构建DTF矩阵，如式(3)所示：

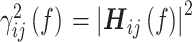3

其中，i，j为DTF矩阵系数的索引。对式(3)进行归一化，如式(4)所示：

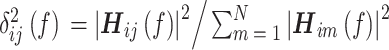4

DTF矩阵归一化后的δ²_ij(f)代表导联j对导联i的影响在所有导联对导联i的影响中的占比，N为DTF矩阵的最大宽度，δ²_ij (f)的值越大，则导联j对导联i的影响越强。

自适应有向传递函数（adaptive direct transfer function，ADTF）是一种时变的DTF方法，它揭示了不同频率下不同大脑区域之间的时变连接。但是由于时间复杂度增加，消耗的计算量巨大，采用ADTF计算的时间要比DTF方法计算时间长数十倍。最终本文选取计算量较小，且适合于时变网络分析的DTF方法计算各节点之间的相互传递关系。

2.3. 脑网络特征参数计算

2.3.1. 图论

复杂网络是大量真实复杂系统的高度抽象，包括规则网络、小世界网络和随机网络。规则网络，是指系统各节点之间用规则的结构表示，网络中任意两个节点之间的连通具有规则性。随机网络，指在由N个节点构成的图中，以概率P随机连接任意两个节点而成的网络。人脑是一种具有小世界和无标度特征的复杂网络系统，是介于规则网络和随机网络之间的小世界网络。图论是描述网络特征的重要工具，是一种定量分析网络特征的方法^[14]。

2.3.2. 聚类系数

在图论中，节点的聚类系数为该节点的邻居节点之间互为邻居的可能，是一种用来度量某个节点周围节点的聚集程度或者集群效应的系数。它反映了一个节点周围网络的集团化程度，即局部区域节点的信息传输能力。在有向网络里，节点i的聚类系数C_i等于与i相邻的m个节点之间实际存在的连接数t_i与这些节点之间可能存在的最大的连接数m × (m − 1)的比值，如式(5)所示：

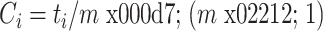5

2.3.3. 全局效率

图论里，网络的最短路径长度度量了整个网络的全局传输的能力，节点间的最短路径越短，说明网络节点连接越密集，传输效率越高。最短路径SP_ij为节点j到节点i之间需要通过几个节点的间隔距离。如果SP_ij为1，则j与i直接相连。若无任何路径能从j到i，则令SP_ij为。整个网络的平均最短路径长度如式(6)所示：

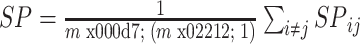6

由于存在SP_ij为的可能，故令全局效率为G，如式(7)所示：

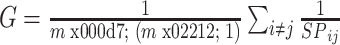7

全局效率能将一些断点置零，计算网络中存在的连通点的网络效率。

3. 实验与分析

3.1. 癫痫脑网络信息传递模型

利用工具箱Econnectome（美国明尼苏达大学的Bin He教授团队开发的一款基于科学计算软件MATLAB的工具包，本研究已获授权可以使用）对14位癫痫患者基于DTF方法的因效性脑网络进行可视化分析。如图2所示，为随机选取的4号癫痫患者在不同状态下（发作间期、发作前期和发作期）各频段的部分因效性脑网络图。由于癫痫的发病类型和病灶区域不同，所以不同癫痫患者的脑网络拓扑结构及信息流向具有个体差异性，但也具有一定的规律性。从频率、状态和空间三个维度，对14位癫痫患者的因效性脑网络图进行动态分析，考察患者癫痫发作整个过程脑网络信息流传递。图2中，通路越粗，颜色越深，则代表节点之间的影响强度越强；箭头所指部分为某点对所指节点的传递方向。

图 2.

Causal brain network map of patient 4

4号患者的因效性脑网络图

由于预处理后的EEG信号频带范围在1～80 Hz，计算所有患者的DTF矩阵，共有80层，每层代表相应频率的DTF矩阵。根据EEG信号的频段划分，将上述80层DTF矩阵分别按照δ波(0.5～3 Hz)、θ波(4～7 Hz)、α波(8～13 Hz)、β波(14～30 Hz)和γ波(>30 Hz)所对应的频率进行加权平均，最终合并为5个DTF矩阵。每个DTF矩阵对应着EEG信号各频段中各导联之间的传递系数。

3.1.1. 从频率维度分析

癫痫发作间期，所有子频段的节点连接紧密，信息传递路径处于随机状态，1号、4号和10号患者δ波、θ波、α波在病灶区域有信息流出强度比较大的连接。癫痫发作前期，随着频率的增加，因效性脑网络中的整体连接程度逐渐降低，并且网络拓扑结构趋近于左右对称，δ波、θ波、α波在病灶区域信息流出强度将进一步增强。癫痫发作期，θ波、α波在病灶区域信息流出强度持续增强，并呈现聚集状态。

3.1.2. 从癫痫状态维度分析

癫痫发作间期所有频段的因效性脑网络趋向于随机网络的状态，节点之间的连接比较紧密。癫痫发作前期所有频段的因效性脑网络趋向于规则网络的状态，节点之间的连接明显减少，存在明显的枢纽节点，病灶区属于枢纽节点之一，从枢纽节点有明显的信息流出，强度高于发作间期。癫痫发作期的因效性脑网络趋向于规则网络的状态，网络的稀疏程度与发作前期相同，但是从枢纽节点流出的信息强度要高于发作前期。

3.1.3. 从空间维度分析

从发作间期经过发作前期到发作期，整个脑网络的节点连接呈现出逐渐下降的趋势，各脑区之间的节点通路连接数减少，但是在额区、颞区、枕区的内部节点之间的通路连接数增加，由顶区至额区或顶区至颞区的信息传递强度有不同程度的增加。

3.2. 脑网络特征参数分析

胡云奉^[7]在研究中确定了功能脑网络的阈值设定策略：① 大脑网络应是一个连通图，即大脑内不存在孤立的与其他无联系的脑区；② 大脑的平均度值k要大于In(N)；③ 网络密度要小于50%。本文以0.01为步长，从0.01遍历至0.99作为矩阵的一系列阈值，对5个频段中的传递矩阵进行二值化操作。计算每个阈值对应二值矩阵的网络稀疏度、平均度值以及连通性。条件 ①② 确定了阈值的最大值，条件 ③ 确定了阈值的最小范围，最终本文选择阈值范围内的最小值，以使得脑网络密度接近50%，如表1所示为14个患者的阈值。

表 1. Thresholds for constructing causal brain networks in 14 epileptics.

14名癫痫患者的阈值

患者编号	1	2	3	4	5	6	7	8	9	10	11	12	13	14
阈值	0.03	0.03	0.03	0.03	0.03	0.03	0.03	0.04	0.03	0.03	0.04	0.04	0.04	0.04

利用表1中的阈值对患者的所有状态定向传递矩阵进行二值化，以二值矩阵来表征一个复杂网络，通过图论的方法求取了该网络的特征。本文选择聚类系数和全局效率两个特征参数，利用秩和检验进行统计学分析，确定不同特征参数在癫痫发作间期、发作前期和发作期之间的差异是否具有统计学意义，当P < 0.05，则差异具有统计学意义，最后分别计算5个频段内脑网络中每个节点的聚类系数和5个频段脑网络的全局效率。

如图3 所示，为14名癫痫患者在三个不同状态下5个频段脑网络的全局效率的均值标准差。其中，δ波和θ波在发作间期和发作期的全局效率的差异不具有统计学意义（P > 0.05），而发作前期的全局效率明显低于发作间期和发作期，差异具有统计学意义（P < 0.05）。α波、β波和γ波的发作期全局效率明显高于发作间期和发作前期，其中β波三个状态的全局效率差异具有统计学意义（P < 0.05）。

图 3.

Global efficiencies of different frequency bands

不同频段的全局效率

如图4所示，为14名癫痫患者在三个不同状态下5个频段脑网络中19个节点的聚类系数的均值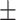标准差。从状态维度分析，不同频段的脑网络在19个节点的聚类系数变化趋势表现为发作前期大于发作期，发作期大于发作间期。从空间维度分析，Fp1、F3、O1、F7、T3、T5、Fp2、F4、O2、F8、T4、T6节点的聚类系数的变化趋势表现为发作前期和发作期远大于发作间期，而Fz、Cz和Pz的聚类系数较低。从频率维度分析，5个频段脑网络所有节点聚类系数都呈现出发作前期、发作期大于发作间期的趋势，但是δ波和γ波的脑网络各节点上的聚类系数在发作前期和发作期上的差异不具有统计学意义（P > 0.05），θ波、α波和β波在额区和颞区发作前期和发作期的差异具有统计学意义（P < 0.05）。

图 4.

Clustering coefficients of different frequency bands

不同频段的聚类系数

4. 讨论

本研究从发作间期、发作前期和发作期不同状态分析癫痫脑网络的动态拓扑结构和网络属性，研究癫痫EEG信号脑网络信息传递途径及动态变化过程。研究结果表明，随着频率的增加，因效性脑网络中的整体连接程度逐渐降低，并且网络拓扑结构趋近于左右对称。从癫痫发作间期—发作前期—发作期，患者的因效性脑网络表现为从趋向于随机网络过渡到趋向于规则网络，这与Ponten等^[15]研究结果相同，即癫痫脑网络的拓扑结构表征出患者状态的动态变化。从癫痫发作前期开始，在病灶区就出现枢纽节点有高强度的信息流出，这与Lopes等^[16]研究结果一致，即癫痫发作之前，病灶区域内各节点处于动态平衡的稳定状态，随着发作的开始，病灶逐渐与周围的区域建立了连接，在癫痫发作的进程中，病灶区域的稳定协调工作状态将被打破，即病灶附近的枢纽节点有大量的信息流出，同时也会有一些节点连接断开，使得无法再进行有效地信息传递。这种情况主要是由于神经元的异常放电过程导致局部的信息传递增强，同时切断了与其他神经传递介质之间的信息传递过程，导致部分脑区域的功能减退。从聚类系数的空间维度分析，在额区、颞区、顶叶区的聚类系数明显增加，这说明从发作间期到发作期，整个脑网络的节点连接呈现出逐渐下降的趋势，各脑区之间的节点通路连接数减少，但是在额区、颞区的内部节点之间的通路连接数增加，由顶区至额区或顶区至颞区的信息传递强度有不同程度的增加。在癫痫发作期各脑功能区相互之间的信息传递强度减弱，而功能区内部各节点的信息交互反而增强，但这种增强是一种“无效”的工作状态，因为它不能有效地与其他脑区进行信息交互。He等^[17]发现癫痫患者在颞区和额区子系统内部的交互作用减弱，证实了脑网络是一个动态的跨区域交互系统，在癫痫发作状态下脑网络动态信息传递出现异常。He等^[18]的研究结果与本文结论基本吻合。癫痫患者在发病时，会丧失思维功能、听觉功能、体感功能等，这些都是由于癫痫脑网络的信息传递途径的动态变化造成的。

人脑对信息进行处理的过程是在数十毫秒内完成的，所以时变网络模型才能揭示大脑的动态信息处理机制。根据动态有向功能性连接网络，找出从癫痫发作间期到癫痫发作期间的脑网络信息传递途径及动态特征变化，从而为癫痫病理机制的理解、癫痫病灶的定位和癫痫发作预测提供更多的思路。

5. 结论

针对癫痫发作机制复杂性以及癫痫发作预测和病灶定位等问题，本文基于DTF构建癫痫EEG信号有向功能性连接网络，从频率、状态和空间三个维度综合分析癫痫脑网络信息传递模型的信息传递途径及动态变化过程。最终结果显示，从发作间期到发作期癫痫脑网络的拓扑结构由趋向随机网络转变成趋向规则网络，整个脑网络的节点连接呈现出逐渐下降的趋势，在病灶区域存在大量信息流出的枢纽节点。在癫痫发作前期所有频段癫痫脑网络的全局效率明显降低，在癫痫发作期又增加。在额区、颞区和枕区附近所有频段癫痫脑网络的聚类系数变化趋势为发作前期大于发作期，发作期大于发作间期。本文的研究结果表明，癫痫因效性脑网络的拓扑结构和特征属性可以反映出癫痫发作的动态变化过程，今后在癫痫病灶的定位和癫痫发作预测方面或将具有重要的研究价值。

重要声明

利益冲突声明：本文全体作者均声明不存在利益冲突。

作者贡献声明：韩凌，研究构思与方法设计，撰写稿件。宋鑫轲，数据处理与撰写稿件。

李春胜，研究方法指导以及论文的审阅与修改。

Funding Statement

国家自然科学基金资助项目（61771323）；辽宁省自然科学基金（2021-KF-12-11）；2020年辽宁省高等学校创新人才支持计划；辽宁省教育厅基金（LJGD2020012）

National Natural Science Foundation of China; Natural Science Foundation of Liaoning Province; Liaoning Province Innovative Talents Support Program for Colleges and Universities in 2020; Liaoning Provincial Education Department Fund