基于子带包络和卷积神经网络的心音分类算法

Abstract

Automatic classification of heart sounds plays an important role in the early diagnosis of congenital heart disease. A kind of heart sound classification algorithms based on sub-band envelope feature and convolution neural network was proposed in this paper, which did not need to segment the heart sounds according to cardiac cycle accurately. Firstly, the heart sound signal was divided into some frames. Then, the frame level heart sound signal was filtered with Gammatone filter bank to obtain the sub-band signals. Next, the sub-band envelope was extracted by Hilbert transform. After that, the sub-band envelope was stacked into a feature map. Finally, type Ⅰ and type Ⅱ convolution neural network were selected as classifier. The result shown that the sub-band envelope feature was better in type Ⅰ than type Ⅱ. The algorithm is tested with 1 000 heart sound samples. The test results show that the overall performance of the algorithm proposed in this paper is significantly improved compared with other similar algorithms, which provides a new method for automatic classification of congenital heart disease, and speeds up the process of automatic classification of heart sounds applied to the actual screening.

引言

先天性心脏病（congenital heart disease，CHD）占所有先天性出生缺陷的近三分之一^[1]。CHD危害极大，及早发现并进行医疗干预是降低患者死亡率的关键，因此尽早对儿童和青少年进行CHD筛查尤其重要。心音是由心房与心室的收缩和舒张、瓣膜运动、血流的相互作用引起。此外，还有一些由于心脏结构和功能缺陷所致的杂音^[2]。心脏听诊是目前在筛查领域的一种重要手段，它依据心音与杂音的特点辅助临床医生进行诊断。但人类听觉感知在分析心音中的隐藏信息方面存在局限性，有时医生很难通过听诊来分析心音，从而影响心音诊断的准确性。

由于上述原因，近年来对心音的自动分析研究成为了人工智能在临床应用的一个重要课题。心音图（phonocardiogram，PCG）是借助电子听诊器采集得到心音信号的图形表示，含有能反映心脏功能及心脏生理、病理的重要信息。因此可以通过分析PCG信号来诊断心血管疾病。本文研究目的在于提高心音自动分类技术和CHD筛查效率，降低CHD的死亡风险。

基于计算机的PCG信号分析流程可以总结为以下三个步骤：① 预处理；② 特征提取；③ 分类器的构建。本文研究的重点是PCG信号分析的特征提取部分。典型用于PCG信号分析的特征大致可分为以下几类：时域特征、频域特征、时频域特征^[3]。国内外有大量研究者长期将PCG信号的特征提取作为一个重要研究课题。Schmidt等^[4]在5个不同频段中采用了参数谱模型、瞬时频率、倍频程功率等方法提取频谱特征，同时组合多个特征，最后评估得到受试者工作特性（receiver operating characteristic，ROC）曲线与坐标轴围成的面积（area under curve，AUC）为0.73。Chen等^[5]使用短时傅里叶变换（short-time Fourier transform，STFT）提取心音幅度谱，在39个测试样本中取得了0.954 9的准确率。Zabihi等^[6]从时域、频域、时频域提取了18个特征，例如梅尔频率倒谱系数（mel-frequency cepstral coefficients，MFCC）、功率谱密度等，最后在测试集上得到0.859的准确率。Rubin等^[7]利用卷积神经网络（convolutional neural networks，CNN）对时频域提取的MFCC特征进行训练，最后测试准确率为0.848。Maknickas等^[8]采用梅尔对数频率系数（log mel-frequency spectral coefficients，MFSC）与CNN，在304例测试样本上获得了0.841 5的准确率。Kay等^[9]将心动周期的时域特征、时频域特征和复杂特征（例如频谱熵、标准偏差等）利用主成分分析（principal component analysis，PCA）进行降维并融合特征，最后该算法在测试集上获得了0.852的准确率。Hamidi等^[10]利用MFCC和分形维数相结合对PCG信号进行分类，并在六个不同的数据集上进行测试，其中三个数据集中达到了0.92、0.81和0.98的准确率。

上述研究中，有些算法研究应用在心音分类上的准确率较高，但是离应用于机器智能辅助听诊阶段还有差距。文献[5]在少量的测试样本中取得了高准确率，普适性有待验证。文献[6]和文献[9]均提取了多种特征，但提取多种特征耗时高、计算复杂，并且实验准确率还有待提升。文献[4]和文献[9]的算法在进行特征提取前都要对PCG信号进行准确地分割。然而在噪声环境下很难准确地分割出基本心音，目前也没有一个较好的方案来解决此问题^[11]。文献[4]利用与时间相关的隐马尔可夫模型分割心音，但个体心音主成分存在差异，所以很难建立一个统一的模型去进行分析。文献[9]是基于心电图（electrocardiogram，ECG）信号对PCG信号进行分割，此方法需要对ECG信号和PCG信号进行同步记录，但对于新生儿来说ECG信号采集比较困难^[12]。对于CHD，能在婴幼儿时期发现并及时治疗，会提高患者存活率。但上述研究使用的数据集来源没有大量涵盖婴幼儿，是否能适用于婴幼儿的筛查还是个未知数。

针对以上问题，本文使用了一种基于子带包络的时频特征提取方法，并搭建了两种CNN模型对其验证。该特征提取方法不需要对PCG信号进行准确分割，减少了计算量。本文在实验中使用的数据集大部分针对低年龄阶段的孩童，以求能在实际筛查中及时发现患者。

1. 模型与方法

1.1. 数据来源

本文研究所用的心音数据库由实验室研究团队采集构建，其数据来源于云南省阜外心血管病医院的临床患者以及在云南省各地州开展CHD免费筛查救治活动时的儿童。作为数据采集来源的志愿者，其年龄限定在6个月至18岁，所有志愿者均签署了知情同意书。本研究及所有数据均已通过云南大学人体研究材料伦理委员会以及云南省阜外心血管病医院伦理委员会的审查并批准使用。数据库中的每一例阳性病例都由心脏病专科医生根据临床听诊和超声心动图确认和记录。本实验室自行研发了一套PCG信号采集设备。采集设备为The ONE心音传感器（Thinklabs Medical LLC，美国），其输出为模拟音频信号，采样频率（frequency of sample，Fs）为5 000 Hz，采集时长为20 s。

1.2. 心音自动分类流程

在对心音进行分类前，需要对心音组成有个基本的了解。按照心音的产生时间和产生机制可以把一个心动周期分为：第一心音（S1）、第二心音（S2）、第三心音（S3）、第四心音（S4）^[13]，通常情况只能听见S1、S2。正确的心脏听诊通常包括分析基本心音（fundamental heart sounds，FHS）和杂音。FHS包括了S1和S2，是心音重要的物理特征。在以往的心音分类研究中，对PCG信号中的FHS进行准确分割是分析PCG信号的前提。但是PCG信号的准确分割是一个有挑战性的难题，不仅计算复杂，而且分割不准确会导致后续分类精度下降。本文提出一种新颖的框架，无需对FHS进行准确分割来分类PCG信号，降低计算量的同时，也避免了心音分割不准确而导致分类器性能下降。

本文研究心音自动分类算法框架如图1所示，具体步骤如下：

图 1.

Flow chart of automatic classification of heart sounds

心音自动分类算法流程图

（1）对PCG信号进行标注，将完成标注的数据分为训练集、验证集、测试集。

（2）对标注信号进行预处理，把一段完整的PCG信号分成小段，每一小段为一帧。

（3）将每一帧的PCG信号分为不同的子带（根据不同频率范围划分），并对每一个子带信号提取包络信号。

（4）对所有的子带包络下采样到特定的点数，将其堆叠得到特定尺寸的特征图（将一维的数据转换为二维）。

（5）将得到的训练集与验证集特征图放进分类器进行训练和分类，得到算法模型。

（6）使用测试集评估模型性能。

1.3. 预处理

PCG信号的预处理通常指心音分割等步骤。但PCG信号分类的主要目的是检测信号中是否存在异常而不是进一步去识别它，所以无需对心音进行精确分割^[14]。本文采用的预处理方法借鉴了语音信号处理中常用的分帧方式，即使用持续时间的窗口对心音进行逐帧处理^[15]。分帧过程是将一个完整的PCG信号样本分为等长的小段，这在一定程度上起到了扩充数据的作用。在后续的分类过程中每一帧的PCG信号都会有一个分类结果，因此最终结果采用多数投票算法进行综合判定。本文研究中，选取的固定帧长为2 s，帧移1 s，如图2所示。正常人平均心率为60～100 次/min。但受生理或者病理的影响，可能导致心率低于或超过此范围。本文选择固定帧长为2 s的原因，就是为保证每一帧都能确保至少有一个完整心动周期存在。帧移是为了在帧与帧之间保留重叠部分数据，以满足连续的要求。通常帧移长度能使帧与帧之间重叠50%。

图 2.

Frame division of heart sound signal

PCG信号的分帧

为使分帧后的PCG信号更平稳，选择长度为2 s的图基窗进行加窗操作。图基窗的特点是旁瓣峰值比低，旁瓣衰减斜率较小，可以有效减少频谱泄漏。

1.4. 特征提取

临床上可根据杂音产生的时期和心音包络的形状，协助医生诊断某些心脏疾病。在PCG信号分析中，包络常被提取用于PCG信号的分割^[16]。但目前直接用包络信号当作心音分类主要特征的研究较少。一些基于小波的特征也可以看作是子带包络特征，比如Deng等^[17]根据离散小波分解系数得到类似于子带包络的特征。在本文的自动心音分类系统中，将采取堆叠子带信号包络的方法来构建时频特征。具体步骤如下：

（1）使用伽马通（Gammatone）滤波器组对分帧后的PCG信号进行滤波并得到子带信号。Gammatone滤波器组能够模拟人类听觉系统特点，可以用于音频信号的分解^[18]。其在时域的脉冲响应h（t）如式（1）所示：

1

其中，k为输出增益；t为连续时间；n是滤波器阶数，决定了边缘斜率；B是时间衰减系数，决定了滤波器带宽；f_c是滤波器的中心频率；φ为相位。本文将多个Gammatone滤波器按中心频率梯度叠加成一个带通滤波器组，对PCG信号进行滤波后使每一帧信号转换为不同的子带信号。子带信号数量与滤波器数量相等。在一定程度上滤波器组对信号也进行了降噪处理。其频率响应如图3所示（以16个滤波器为例）。

图 3.

Frequency response of Gammatone filter banks

Gammatone滤波器组的频率响应

（2）将子带信号通过希尔伯特变换计算得到子带包络。希尔伯特变换实际上是连续时间信号x（t）与 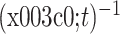之间做卷积^[19]。一个实值信号的希尔伯特变换如式（2）所示：

2

其中 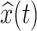是x（t）进行希尔伯特变换后的信号。

实信号进行傅里叶变换时，频谱存在正负频率，即有一半频带携带的信息是冗余的。希尔伯特变换在频域上仅有正频率部分，能起到消除冗余频率的作用。如式（2）、式（3）所示，可以构造复信号z（t），z（t）称为x（t）的解析信号。

3

其中x（t）为解析信号的实部， 构成虚部，j为虚数单位。最后对式（3）求模即可得到信号的包络。

（3）将子带包络下采样到特定的点数。通常采用抽取的方式进行下采样，即通过减少数据样点从而减少运算时间，但可能会造成原始信号特征缺失。本文将子带包络分成若干个点数一致的序列片，对每一个序列片求均值并将其设为下采样后的数值，从而得到新的序列。这种采样方法被称为平均下采样。平均下采样能较好地保存原始信号特征，还能去除高频分量，使包络更平滑。

（4）将平均下采样后的子带包络进行对数运算，如式（4）所示：

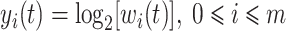4

其中w_i（t）为平均下采样后的子带包络信号，y_i（t）为最终得到的子带包络信号，m的取值由前面Gammatone滤波器数量即子带信号个数决定。通过对信号进行对数运算可以将线性转换为非线性，减少数据间的相关性，有利于后续的分类步骤。对数运算还可以有效对数据进行压缩，使数据更加平稳，方便计算。

（5）将最终处理得到的子带包络y_i（t）进行转置并横向堆叠成一个二维矩阵Y。对矩阵Y进行中心化得到S，并对S进行幅度归一化得到Q，如式（5）和（6）所示：

5

6

其中 为矩阵Y的均值。

（6）将处理后的矩阵Q的系数利用颜色编码对应。其中高值对应较亮的颜色，低值对应较暗的颜色，从而得到特征图。

本文是将PCG信号分帧后才进行特征提取，所以一帧PCG信号对应一张特征图。如图4所示，给出了特征提取的过程。图4中“Ind”指的是将一帧完整PCG信号分成不同子带信息的索引号，由于篇幅限制，中间的省略号指其它的子带信息。图4以32×16的特征图为例，其尺寸分别对应时间序列片数和子带包络数。正常PCG信号与异常PCG信号的特征提取结果图对比如图5所示。图5中异常PCG信号为常见CHD病例，包括房间隔缺损（atrial septal defect，ASD）、室间隔缺损（ventricular septal defect，VSD）、动脉导管未闭（patent ductus arteriosus，PDA）、卵圆孔未闭（patent foramen ovale，PFO）。

图 4.

The overall framework of the feature extraction

特征提取整体框架

图 5.

Comparison of feature extraction results

特征提取结果图对比

1.5. 分类模型

随着人工智能算法的快速发展，在心音自动分析领域，神经网络被用于分类的研究日益渐增，并取得不错的成果。Nilanon等^[20]利用CNN对心音进行分类并与传统分类方式进行了对比。Zhang等^[21]利用长短时记忆神经网络（long short-term memory networks，LSTM）对心音进行分类。因为心音数据库的规模通常来说相对较小，并且本文提取的特征图尺寸较小，使用复杂模型容易导致过拟合现象。据此，本文搭建了两个浅层CNN模型，分别为Ⅰ型与Ⅱ型模型。其中Ⅰ型指具有2层卷积层的CNN，Ⅱ型指具有4层卷积层的CNN。Ⅰ型与Ⅱ型CNN结构示意如图6和图7所示。Ⅰ型与Ⅱ型CNN每一个卷积层都是32个核，卷积核大小为3×3，步长为1×1，激活函数选用线性整流函数（rectified linear unit，ReLU）。池化层选用最大池化，池化核大小为2×2。随机失活（Dropout）层可以有效控制过拟合的现象，Dropout率设置为0.5。展平（Flatten）层用来展平参数，主要用作参数在卷积层与全连接层之间的过渡。本文选用柔性最大（Softmax）回归方法用于分类，Softmax可以将多个神经元输出映射到（0，1）区间内，选取概率最大的结点作为最终输出。本文通过不同特征提取方式和不同卷积层数的CNN模型组合探求适用于临床环境下的心音自动分类技术。

图 6.

Structure diagram of type Ⅰ CNN

Ⅰ型CNN结构图

图 7.

Structure diagram of type Ⅱ CNN

Ⅱ型CNN结构图

2. 实验与分析

2.1. 实验环境与数据说明

本文使用实验环境的硬件配置如下：中央处理器（Core i7-9750H @2.60GHz，Intel，美国），独立显卡（NVIDIA 1660 Ti 6GB, Nvidia，美国）。本文选用的深度学习框架为TensorFlow 2.0（Google，美国），编程语言为Python 3.6（Python Software Foundation，美国）。

为了更有效地进行对比，本文研究实验与对比实验均在同一数据集下进行，数据集来自1.1小节所提的心音数据库。实验使用的数据来自1 000名志愿者的心音，其中正常和异常心音样本比例为1∶1，异常心音病例包括了临床上主要类型的CHD，例如VSD、ASD、PDA、PFO。由于心脏听诊区通常有5个，每个人的心音都按五个听诊点位进行采集，每个点采集时间为20 s，故总的心音数据样本集为5 000例。将训练集、验证集、测试集按照0.65、0.15、 0.2的比例随机划分，即训练集3 250例、验证集750例、测试集1 000例。1 000例测试集数据中正常和异常心音样本比例也为1∶1。对比以往的心音分类研究，本文使用的数据量更大，能最大限度地保证本文算法的鲁棒性。

2.2. 评估指标

为了评估本文所提出的算法，本文的每个实验均使用以下5种评估标准：准确率（accuracy，acc）、灵敏度（sensitivity，se）、特异度（specificity，sp）、F₁、AUC。前三个评估方法的计算公式，如式（7）～式（9）所示：

7

8

9

其中，真阳性（true positive，TP）代表异常心音样本被正确分类的结果数；真阴性（true negative，TN）代表正常心音样本被正确分类的结果数；假阳性（false positive，FP）代表正常心音样本被错误分类的结果数；假阴性（false negative，FN）代表异常心音样本被错误分类的结果数。

F₁分数是分类问题的一个综合衡量指标。一些分类问题的机器学习竞赛，通常把F₁作为最终的测评指标。它结合了精确率（precision，pr）和召回率（recall，re），是这两者间的调和平均数^[22]。其计算公式如式（10）～式（12）所示：

10

11

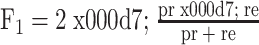12

ROC曲线是重要的统计分析方式。ROC关注两个指标，假阳性率（false positive rate，FPR）和真阳性率（true positive rate，TPR），这两者分别对应横坐标和纵坐标。ROC曲线下方与坐标轴形成的面积AUC是度量模型好坏的一个标准^[23]。AUC越大，表示性能越好。

2.3. 实验结果与分析

为了对比不同卷积层数对分类效果的影响，本文算法对比实验均在Ⅰ型和Ⅱ型CNN模型上进行训练和测试，通过将不同的特征提取方法与不同的CNN模型进行组合来找到最优算法。子带包络方法中的参数设置会导致特征图尺寸不同，从而影响分类效果。为比较特征参数与分类网络的契合程度，以获取最佳分类效果。本文通过选取不同的时间序列片数量和Gammatone滤波器数量进行参数对比实验。时间序列片数量设置为32、64、128。Gammatone滤波器的数量设置为16、32、64。两组参数一一对应，最后得到三种尺寸的特征图，分别为32×16、64×32、128×64。根据上述的评估方法，本文算法与其他算法的对比结果如表1和表2所示。

表 1. Comparison of various algorithms based on type Ⅰ CNN model.

基于Ⅰ型CNN模型的各算法对比

分类算法	心音分类评估标准
	se	sp	acc	F1	AUC
STFT + CNN[5]	0.876	0.896	0.886	0.885	0.939
MFCC + CNN[7]	0.876	0.926	0.901	0.898	0.948
MFSC + CNN[8]	0.872	0.938	0.905	0.902	0.952
子带包络(128 × 64) + CNN	0.892	0.936	0.914	0.912	0.952
子带包络(64 × 32) + CNN	0.912	0.938	0.925	0.924	0.965
子带包络(32 × 16) + CNN	0.938	0.940	0.939	0.939	0.966

表 2. Comparison of various algorithms based on type Ⅱ CNN model.

基于Ⅱ型CNN模型的各算法对比

分类算法	心音分类评估标准
	se	sp	acc	F1	AUC
STFT + CNN[5]	0.862	0.904	0.883	0.881	0.916
MFCC + CNN[7]	0.884	0.874	0.879	0.880	0.914
MFSC + CNN[8]	0.814	0.964	0.889	0.880	0.945
子带包络(128 × 64) + CNN	0.884	0.936	0.910	0.908	0.962
子带包络(64 × 32) + CNN	0.898	0.940	0.919	0.917	0.968
子带包络(32 × 16) + CNN	0.900	0.940	0.920	0.918	0.963

本文对比算法选取文献[5]、文献[7]和文献[8]中的方法。文献[5]采用STFT与CNN进行心音分类。STFT通过对加窗数据进行傅里叶变换从而得到时频图，但会含有过多冗余信息。文献[7]和文献[8]均采用梅尔滤波器组相关特征和CNN结合的算法。其中文献[7]特征提取方法为MFCC，文献[8]为MFSC。MFCC和MFSC能从音频数据捕捉到与人类对响度和音调感知相似的特征，所以在语音信号处理领域非常流行。MFSC与MFCC最大的不同是MFCC在MFSC的基础上又进行离散余弦变换，所以MFSC比起MFCC保留了更多原始特征。从表1与表2的数据来看，四种特征提取方法无论与Ⅰ型还是Ⅱ型CNN模型组合都能较好地对PCG信号进行分类，但是子带包络算法整体性能要优于其它算法。从子带包络参数对比看，32×16的特征图效果最佳，更适合应用于心音分类。在表2中，基于Ⅱ型CNN的MFSC算法的sp高于本文基于Ⅱ型CNN的子带包络算法，对比其它指标却略有欠缺。对于CHD的筛查应用，降低漏诊率是关键，所以提高se比sp更为重要。从两个表中可看出本文算法的se优于其它算法，降低了临床误诊的风险。

如图8所示是不同特征提取方法与不同CNN模型组合实验结果的ROC曲线对比。ROC曲线越靠近左上方表示AUC越大，该系统性能越好。从图8可以看出不同参数设置的子带包络无论搭配2层卷积CNN模型还是4层卷积CNN模型，从整体评估指标上看均优于其它三种算法。PCG信号包络在信号变化时能呈现出不同的特征信息，例如幅度、峰值间隔等。所以包络能很好地表示心音的特征。通过不同频率的子带包络叠加，可以将特征信息更加凸显，作为后续分类会更加有优势。总的来说，子带包络对比STFT、MFCC和MFSC具有更好的性能。

图 8.

ROC curve comparison of each algorithm

各算法ROC曲线对比

通过上述实验结果分析，基于Ⅰ型CNN的子带包络（32×16）优于其它所有对比算法。为了验证此二分类模型对常见CHD的分类有效性，本文单独将测试样本中的500例异常PCG信号进行测试。对常见CHD测试效果如表3所示。可以看出该算法对各类常见CHD能较好地识别，但对于PFO还稍有欠缺。可以从1.4节的图5中发现 PFO-PCG特征图较为接近正常PCG特征图，这是导致准确率稍低的原因。

表 3. Test results of common CHD.

常见CHD测试效果

CHD种类	基于I型CNN的子带包络(32×16)算法
	acc
VSD	0.993
ASD	0.950
PDA	0.904
PFO	0.853

本文算法实验以及对比实验的各项评估指标均在同一测试集上进行测试，并由程序自动计算、统计。对比以往研究，本文使用测试样本数量更多，进一步表明本文所提算法有较好的鲁棒性与泛化能力，可应用于CHD筛查。

3. 结论

针对心音自动分类领域多数算法依赖于心音分割的问题，本文提出了一种基于子带包络的时频特征提取方法，不依赖于对心音的准确分割，在降低了运算复杂度的同时也具备较好性能。首先对PCG信号进行预处理，即分帧操作。然后对帧级PCG信号提取子带包络，将其叠加成二维特征图作为CNN分类的主要特征。最后根据所提取的特征，构建合适的CNN分类器模型。本文使用5种不同评价指标对所提算法进行评估。实验结果表明，本文算法在测试集上的各项指标均取得较好结果，对比其他研究所用的时频特征提取方法，综合性能更佳，为心音自动分类技术应用于CHD筛查提供了可行方法。但本文算法对PFO病例分类准确率还有待提高，今后将加深对这方面的研究，进一步提高算法性能。

利益冲突声明：本文全体作者均声明不存在利益冲突。

Funding Statement

国家自然科学基金资助项目（81960067）；2018云南省重大科技专项资助项目（2018ZF017）

National Natural Science Foundation of China; Yunnan Provincial Science and Technology Department