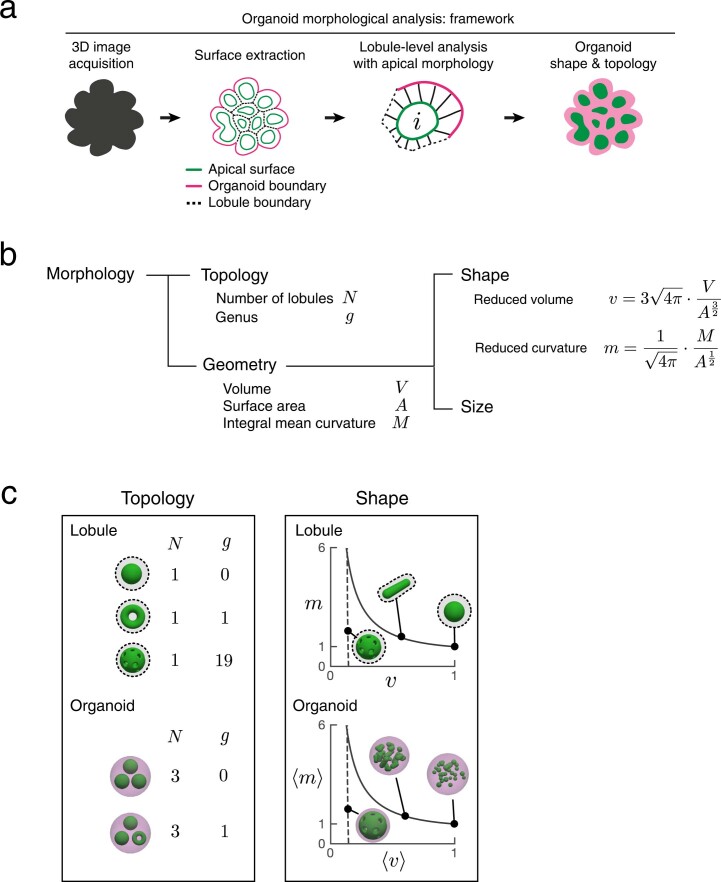
Extended Data Fig. 2. Framework for morphological analysis of organoids.

First, we acquire 3D images of a tissue sample, here, an organoid. Second, we perform image segmentation and surface construction of triangulated meshes to represent 3D tissue morphology as a set of apical surfaces and organoid outer boundary. Next, we use individual apical surfaces to define epithelial lobules and characterize their morphology. Finally, we integrate the information from all lobules to define the overall topology and shape of an organoids. This process is repeated for multiple organoids. b, In mathematical terms, morphology is discussed for the aspects of topology and geometry. Topology describes the connectivity of objects, which do not change from stretching or shrinking. Geometry is discussed in terms of the shape and size of objects. Shape is a scale invariant quality, while size has the units related to length scale. c, The metrics for topology are the number of lobules N and total genus g in an organoid. The metrics for shape are the reduced volume v and reduced curvature m of individual lobules, which are averaged to yield organoid level quantities 〈v〉 and 〈m〉 (see Methods).