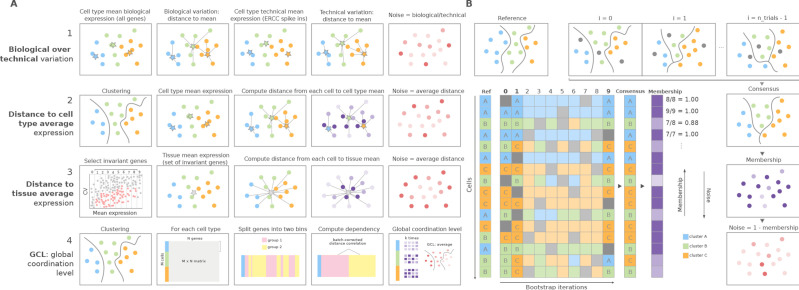
Figure 1. Overview of computational methods for the quantification of transcriptional noise and example workflow in Scallop.
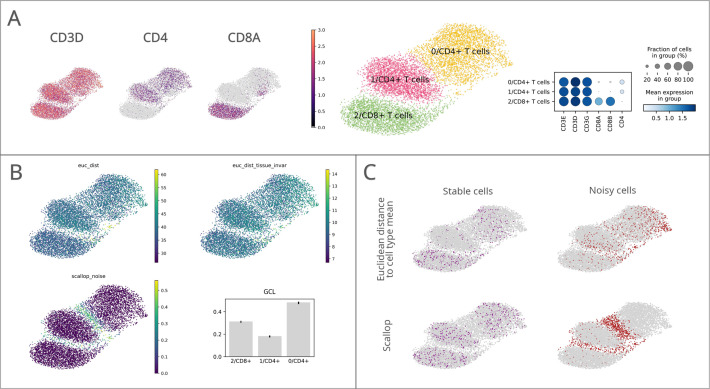
(A) The methods implemented in Decibel Python toolkit are summarized through diagrams depicting how they measure transcriptional noise. (1) Biological variation (whole transcriptome-based Pearson’s correlation distance between each cell and the mean expression vector), divided by the technical variation (External RNA Controls Consortium [ERCC] spike-in based distance; Enge et al., 2017). (2) Mean whole transcriptome-based Euclidean distance to cell type average (Enge et al., 2017). (3) Mean invariant gene-based Euclidean distance to tissue average (Enge et al., 2017). (4) GCL (Levy et al., 2020) per cell type. Stars represent the ‘center’ of each cluster (average gene expression for each cell type). (B) Scallop: example workflow on a 16 cell dataset. A reference clustering solution (Ref) is obtained by running a community detection algorithm (default: Leiden) on the whole dataset. Three clusters are obtained: A (blue), B (green), and C (orange). Then, a subset of cells is randomly selected and subjected to unsupervised clustering n_trials = 10 times (cells not selected in each bootstrap iteration are shown in gray). The cluster labels across bootstrap iterations are harmonized by mapping the cluster labels with the greatest overlap, using the Hungarian method (Munkres, 1957). A consensus clustering solution is derived by selecting the most frequently assigned cluster label per cell, and the membership score is computed as the frequency with which the consensus label was assigned to each cell. Scallop measures noise as a 1 − membership value assigned to each cell.
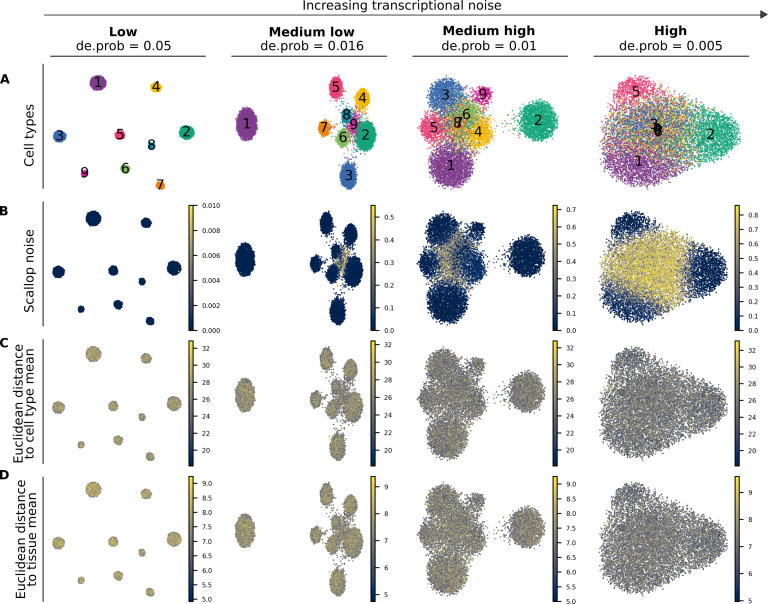
Figure 1—figure supplement 1. Performance of Scallop and two distance-to-centroid methods on four artificial datasets with increasing transcriptional noise.
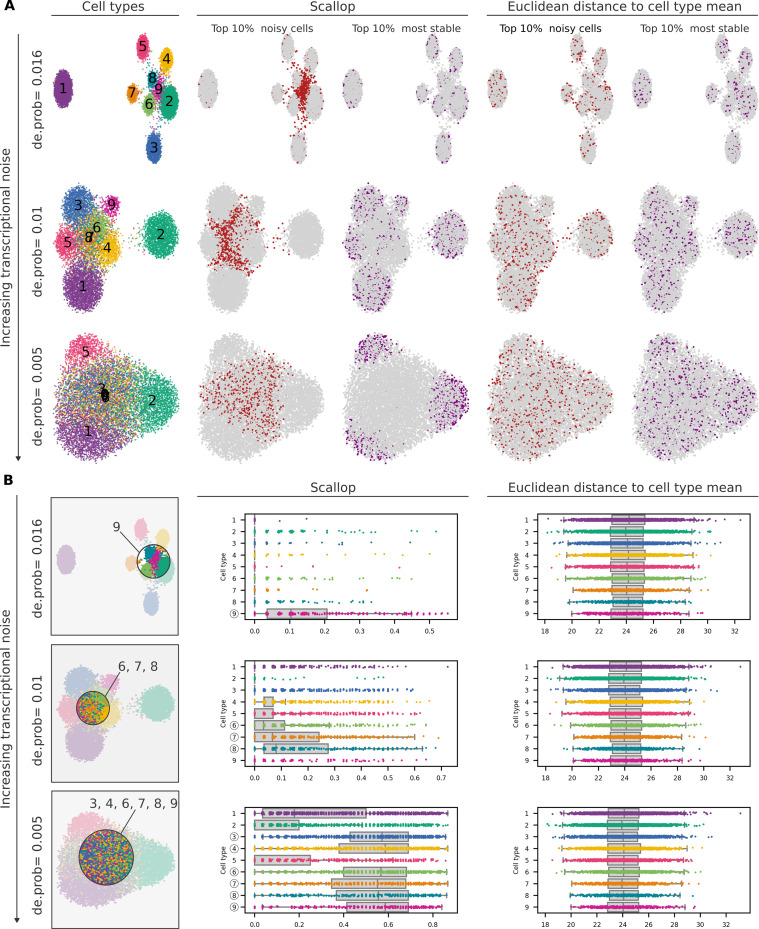
Figure 1—figure supplement 2. Ability of Scallop and a distance-to-centroid method to detect noisy cells within cell type clusters.
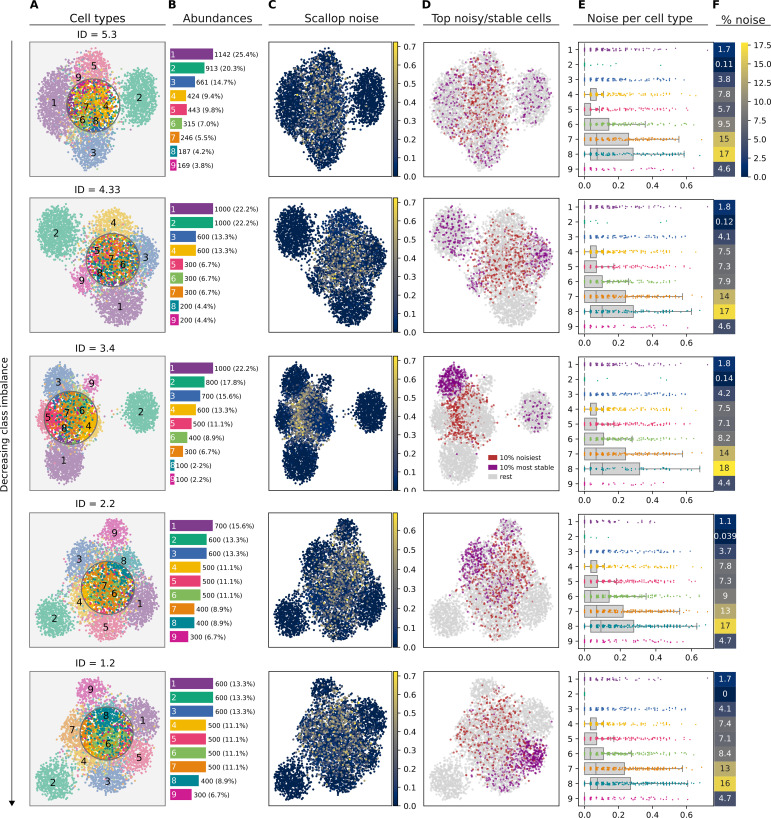
Figure 1—figure supplement 3. Effect of cellular composition on the performance of Scallop.
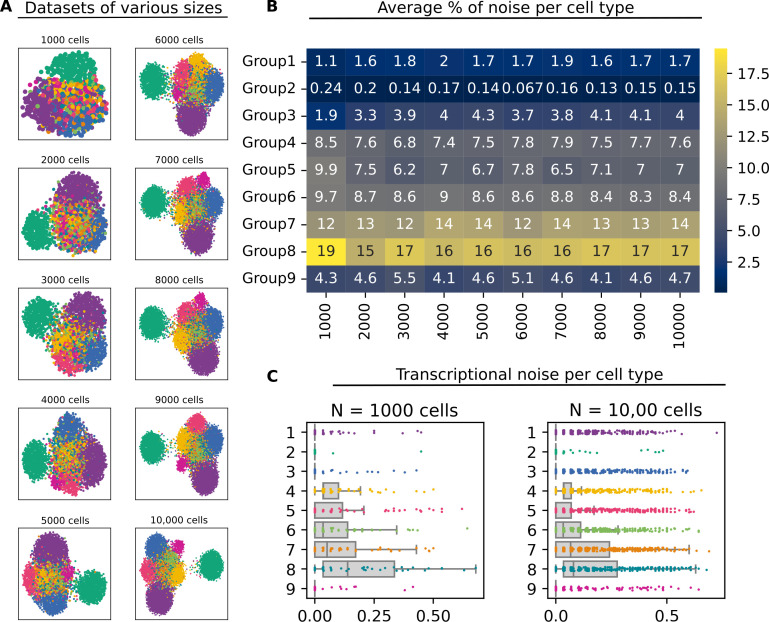
Figure 1—figure supplement 4. Effect of dataset size on the performance of Scallop.
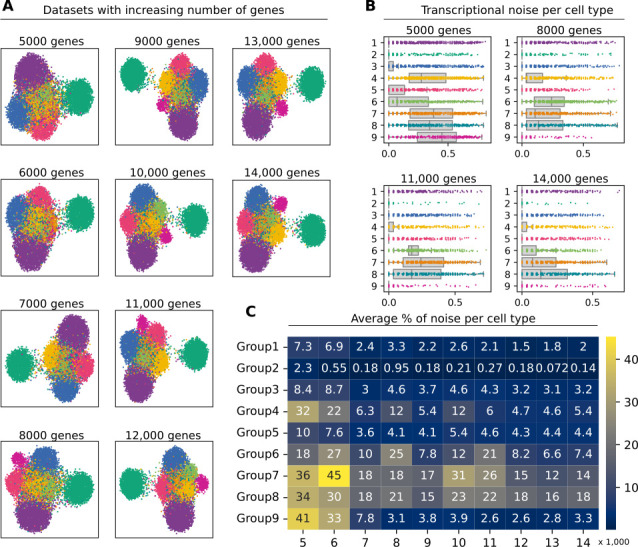
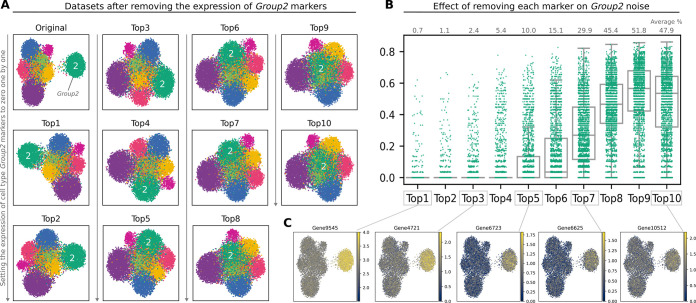
Figure 1—figure supplement 5. Effect of the number of genes on the performance of Scallop.