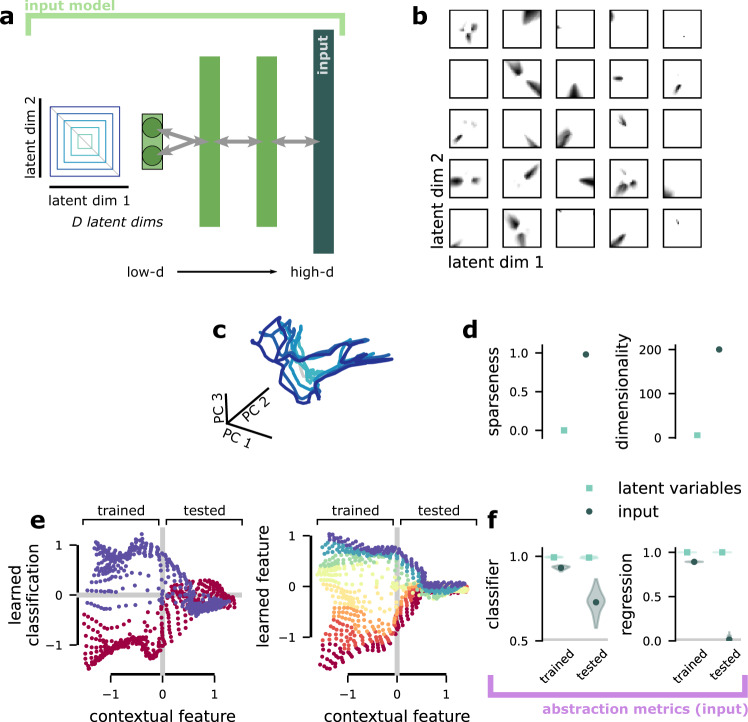
Fig. 2. The input model.

a Schematic of the input model. Here, schematized for D = 2 latent variables. The quantitative results are for D = 5. b The 2D response fields of 25 random units from the high-d input layer of the standard input. c The same concentric square structure shown to represent the latent variables in a after being transformed by the standard input. d (left) The per-unit sparseness (averaged across units) for the latent variables (S = 0, by definition) and standard input (S = 0.97). (right) The embedding dimensionality, as measured by participation ratio, of the latent variables (5, by definition) and the standard input (~190). e Visualization of the level of abstraction present in the high-d input layer of the standard input, as measured by the classifier generalization metric (left) and regression generalization metric (right). In both cases, the y-axis shows the distance from the learned classification hyperplane (right: regression output) for a classifier (right: regression model) trained to decode the sign of the latent variable on the y-axis (right: the value of the latent variable on the y-axis) only on representations from the left part of the x-axis (trained). The position of each point on the x-axis is the output of a linear regression for a second latent variable (trained on the whole latent variable space). The points are colored according to their true category (value). f The performance of a classifier (left) and regression (right) when it is trained and tested on the same region of latent variable space (trained) or trained in one region and tested in a non-overlapping region (tested, similar to e). Both models are trained directly on the latent variables and on the input representations produced by the standard input. The gray line is chance. The standard input produces representations with significantly decreased generalization performance.