Abstract
The aim of molecular coarse-graining approaches is to recover relevant physical properties of the molecular system via a lower-resolution model that can be more efficiently simulated. Ideally, the lower resolution still accounts for the degrees of freedom necessary to recover the correct physical behavior. The selection of these degrees of freedom has often relied on the scientist’s chemical and physical intuition. In this article, we make the argument that in soft matter contexts desirable coarse-grained models accurately reproduce the long-time dynamics of a system by correctly capturing the rare-event transitions. We propose a bottom-up coarse-graining scheme that correctly preserves the relevant slow degrees of freedom, and we test this idea for three systems of increasing complexity. We show that in contrast to this method existing coarse-graining schemes such as those from information theory or structure-based approaches are not able to recapitulate the slow time scales of the system.
Short abstract
Coarse-graining is a popular approach to study large and complex macromolecular systems. We propose the optimization of coarse-grain mapping to preserve the slow dynamical processes of a system.
Introduction
Numerical simulation of complex high-dimensional systems in biophysics and condensed matter has become a powerful tool for the understanding of processes that can not be directly observed in wet lab experiments. The significant advances in hardware and software of the last couple of decades now allow one to routinely simulate medium size proteins at atomistic resolution and microsecond time scales. With dedicated hardware,1 or bias-enhanced sampling techniques,2,3 or distributed simulations combined with Markov state models (MSMs),4 it is possible to reach the millisecond time scale and sample folding and binding events and large conformational changes.5−7 From these long-time scale simulations, it is clear that the relevant structural, thermodynamic, and kinetic information for many biomolecular processes can be significantly simplified and expressed in lower-resolution models.8−11 Rare-event transitions such as folding, binding, and conformational changes can often be well described in terms of a few collective variables, as supported both by statistical mechanics arguments12 as well as plenty of empirical evidence resulting from transfer operator theory8,13 and Markov modeling.4,14 Consequently, it should be possible to summarize the essential properties of structure, thermodynamics, and kinetics that are relevant for the long-time scale behavior with a molecular model with fewer degrees of freedom.
Indeed, coarse-grained (CG) models, which implement this idea explicitly by representing groups of atoms as coarse-grained beads have long been used in the study of large molecular systems10,15−17 and have been useful to extend the reach of simulations to longer time scales and larger system sizes. The ability of a CG model to reproduce the relevant physics of a molecular system relies on two closely connected aspects: (1) the choice of the CG resolution and the corresponding degrees of freedom (usually referred to as “CG mapping”) and (2) the design and parametrization of the associated effective energy function. Several design principles to tackle the second of these tasks have been proposed to obtain a CG energy once the resolution is set. These include (i) bottom-up CG approaches via force-matching, relative entropy minimization, or Boltzmann inversion18−20 where the CG model is designed to reproduce the same coarse-grained thermodynamics of an all-atom model, (ii) fitting a set of observable quantities to the corresponding ones obtained in all-atom simulation and/or experimental data,21,22 or (iii) the minimization of frustration in model protein systems.16 In addition, the flexible parametrization of the CG energy using neural networks has recently received great attention.23−29
On the other hand, the systematic selection of a suitable CG mapping, i.e., which degrees of freedom to retain upon coarse-graining, is a task that has received comparatively little attention30,31 and is often left to the scientist’s chemical intuition. The success of a CG model is often assessed a posteriori by comparing the results of CG simulations with their all-atom counterpart or experimental data, however, such a comparison can not disentangle the effects associated with the CG mapping from the ones associated with the choice of energy function.23,32−37
One of the first approaches to quantify the “goodness” of a given CG mapping for the parametrization of a CG energy was introduced via the definition of the mapping entropy (Smap) as part of a relative entropy framework19—also known as likelihood-based training of energy-based models in machine learning.38Smap depends only on the CG mapping (i.e., it is not affected by the choice of the CG energy), and its absolute value quantifies the amount of information lost upon coarse-graining. Following this idea, the minimization of the absolute value of Smap (or, equivalently, the maximization of its signed value, see Methods for details) has been proposed as a criterion for selecting a CG mapping at a given resolution.39 While the initial work was demonstrated on harmonic systems where Smap can be analytically computed, the applicability of the method has been later extended40 by deriving a numerical approximation of Smap that enables its estimation for more complex systems.41,42
In later work, it was noted that the maximization of Smap for the selection of an optimal CG mapping preserves upon coarse-graining mostly information associated with local high-frequency motions rather than global processes.43 The same authors proposed as an alternative approach the selection of a mapping scheme by optimizing a different quantity, the Vibrational Power, defined as the trace of the mass-weighted covariance matrix of the CG coordinates. This quantity allows an estimate of how well a CG model preserves large-scale motions.43
In parallel, different groups have proposed to define CG mapping schemes based on their ability to recover all-atom coordinates, e.g., by learning a CG mapping and all-atom reconstruction simultaneously via an autoencoder25 or by other machine learning approaches that employ structural classification or reconstruction errors (RE).44−46
In this work, we systematically investigate the effect of CG mapping on its ability to reproduce the long time scale processes of the system. We follow an orthogonal direction compared to previous approaches and exploit the Variational Approach for Markov Processes (VAMP)47 in order to propose the selection of an optimal CG mapping that explicitly maximizes the CG model’s ability to reproduce long-time scale processes. By means of a careful comparison, we find that such a VAMP-optimized CG mapping substantially disagrees with existing approaches.
Results and Discussion
We first
discuss the general idea of our approach and then demonstrate
it on three separate systems of increasing complexity (see Figure 1): (1) a 4-bead harmonic
chain, (2) a Gaussian Network Model (GNM) of a protein, and (3) a
model protein previously studied in the literature that is capable
of adopting folded, misfolded, and unfolded conformations.48 For each choice of linear mapping 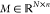 from the fine-grained
coordinates
from the fine-grained
coordinates 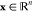 to the CG coordinates
to the CG coordinates 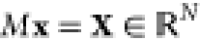 , we consider the effective
CG energy, W(X), that is thermodynamically
consistent
with the full resolution model with energy u(x):18
, we consider the effective
CG energy, W(X), that is thermodynamically
consistent
with the full resolution model with energy u(x):18
| 1 |
where β is the inverse temperature. For systems 1 and 2, we can obtain the thermodynamically consistent CG energy function analytically, as well as the partition function and all ensemble averages (see the Supporting Information for detail). For system 3, the thermodynamically consistent CG energy can not be computed analytically, and one would need to use, e.g., a machine-learning approach to approximate it numerically.23,26 However, we do not need an expression for the CG energy to evaluate the different metrics for the selection of the optimal mappings as they can be computed from equilibrium trajectories of the underlying high resolution reference model (see the Supporting Information for detail).
Figure 1.
Visualization of the 3 systems studied. (A) Simple 4-bead harmonic chain. Here each bead is treated the same, and k1 and k2 represent the strength of the spring. (B) Gaussian network model from the Cα atoms of protein 2ERL with a neighbor cutoff of 10 Å. (C) Model protein system, as defined in ref (48), representative of a protein hairpin. Pairs of beads with equal color have attractive interactions.
We choose here to focus on simple and small systems instead of a more realistic protein model for ease of interpretation (system 1), to be able to obtain analytical results (system 2), and/or to enumerate all possible mapping choices and exhaustively compare the different metrics (system 3).
We show that in all cases a mapping scheme can be clearly and efficiently selected to best capture the long-time dynamics of a system even for highly nonlinear systems, a direct advantage over methods that must make linear approximations or ignore the time evolution dimension of the system.
Defining the CG Mapping Criterion via the Variational Approach for Markov Processes (VAMP)
In the analysis of molecular dynamic (MD) simulations, one often seeks to define reaction coordinates that are able to characterize the slowest processes, or rare-event dynamics.49 On long time scales, the equilibrium molecular dynamics of molecules with rare events can be expressed in terms of the dominant eigenvalues and eigenfunctions of the dynamical propagator, such that these eigenfunctions are a natural choice for the rare-event coordinates.4,13 The Variational Approach for Conformation dynamics (VAC)50,51 is a framework to systematically approximate the rare-event eigenfunctions, which is achieved by maximizing the VAC score. When representing these functions with a linear combination of basis functions, one obtains the Time-lagged Independent Component Analysis (TICA) algorithm52,53 as a result. However, the score can also been used in a more general setting, for example, in the training of neural networks to find a nonlinear representation of the rare event coordinates.54−56 Recently, VAC has been generalized to the variational approach for Markov processes, which also permits the dynamics to be out of equilibrium47 and is closely connected to Koopman theory for dynamical systems.57−59
The VAMP score is a quantity that can be easily computed from simulated trajectories and assesses the ability of a set of variables to describe the slow dynamics of the system: the higher the VAMP score, the more appropriate the set of coordinates to serve this purpose. The VAMP score for reversible dynamics can be written as47
| 2 |
| 3 |
| 4 |
where Xt is the vector containing the
values of all the selected coordinates
at time t, Xt+τ contains
the values of such coordinates after a lag time τ, and 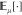 is the expectation value computed with
the equilibrium probability distribution of the full resolution model.
The matrices C00 and C0τ are the covariance matrix and the time-lagged
covariance matrix, respectively. For the harmonic systems studied
here, the VAMP score, as well as other scores to assess the quality
of the CG mapping can be computed analytically, except for the reconstruction
error (See Methods for the derivation of these
expressions).
is the expectation value computed with
the equilibrium probability distribution of the full resolution model.
The matrices C00 and C0τ are the covariance matrix and the time-lagged
covariance matrix, respectively. For the harmonic systems studied
here, the VAMP score, as well as other scores to assess the quality
of the CG mapping can be computed analytically, except for the reconstruction
error (See Methods for the derivation of these
expressions).
Recently, the VAMP score has been used for selecting optimal features for constructing Markov state models such that the rare-event dynamics of the molecule are best-resolved.60 Here we propose to use the VAMP score in order to define the CG mapping: for a fixed resolution, the selection of CG degrees of freedom that best capture the long time scale dynamics also need to maximize the VAMP score among all possible CG mapping schemes.
In the following, we discuss the results on three model systems, while the detailed calculations are reported in the Methods section and in the Supporting Information.
4-Bead Model System
We start by examining a simple symmetric 4-bead harmonic chain (Figure 1A) with the Hamiltonian
| 5 |
For this system, we can obtain analytical results of thermodynamic and kinetic quantities and exhaustively enumerate all possible CG mapping schemes.
In the coarse-graining community, there are two primary styles of mappings: (i) “slicing”, whereby individual atoms are selected to represent the coarse-grained beads, or (ii) “averaging”, where multiple atoms are used to represent a bead and their properties averaged.61 Here we consider all possible slicing and averaging mappings from the 4 “atom” system into 2 CG beads. In the averaging mappings, we assign the same weight to each atom assigned to the same bead.
By varying the relative stiffness of the springs between the beads (k1 < k2 or k1 > k2) we obtain different optimal mappings (Figure 2). In the case of a stiffer spring in the middle and softer springs at the edges (k1 < k2), a CG mapping retaining beads 2 and 3 only describes the fast fluctuations that are usually not of interest. However, this is the CG mapping scheme maximizing the (negative) value of the mapping entropy. On the other hand, the maximization of the Vibrational Power and of the VAMP score, as well as the minimization of the reconstruction error, yields the same CG mapping corresponding to the selection of the first and last bead of the chain, therefore describing the largest (and, in this case, slowest) fluctuations.
Figure 2.

Comparison between different CG mapping methods for the 4-bead harmonic chain. The top part shows the results for the case k1 < k2 (soft spring at the edges) while the bottom part for k1 > k2 (soft spring in the center). The different mapping metrics are reported for each of the considered CG maps (illustrated by the cartoons in the middle), with the optimal values indicated by a star.
The situation is quite different for the case of a softer spring in the middle (k1 > k2), which can be considered a toy model of a molecule where hydrogen atoms are bound with a very stiff spring to two central atoms (e.g., hydrogen peroxide H–O–O–H). As high energy fluctuations have a dominant effect on the evaluation of Smap, the maximization of the (negative) value of Smap, in this case, selects to preserve the fast motion associated with the first two (or equivalently the last two) beads. Interestingly, this is the mapping scheme also selected by the minimization of the reconstruction error. The maximization of the Vibrational Power again preserves the motion of the largest amplitude,selecting the first and last beads. However, in this case, this CG mapping does not correspond to the one preserving the slowest motion, which is instead given by the maximization of the VAMP score and yields an averaging scheme that takes into account also the contribution of the two middle beads (see Figure 2).
The physical meaning of the difference between the maximization of the Variational Power and the maximization of the VAMP score is analogous to the difference in the selection of reaction coordinates by methods such as Principal Component Analysis (PCA), which describes the largest amplitude motions, as opposed to methods such a TICA, describing the slowest processes. It is well-known,53 that PCA and TICA can give very different results as the amplitude of a motion does not necessarily report on its time scale. Therefore, if the interest is the preservation of the slowest processes upon coarse-graining, once the resolution is selected, the CG mapping maximizing the VAMP score should be considered.
Gaussian Network System
In order to further illustrate the divide between the different mapping criteria but still be able to obtain analytical solutions, we consider a Gaussian Network Model (GNM) of a protein. Gaussian network models have been used extensively in the past for proteins as their simplicity allows for fast, interpretable results that in general give qualitative agreement with experimental results.62,63 GNMs typically select carbon alpha (Cα) atoms in the protein backbone and model with a harmonic spring the interaction between any Cα pairs that lie within a preset cutoff distance in the native structure.64 As usual for GNMs, all these springs are modeled with equal spring constants, so in contrast to the 4-bead system above, the GNM dynamics depend on the degree of connectivity between beads rather than the strength of individual springs.
Following ref (43), we consider the GNM of the 40-residue protein 2ERL. Given the small size of the protein, we can enumerate a large number of CG mappings for different numbers of CG beads. We consider all the possible partitions of the 40 Cα’s into N = 2, 3, 4, 5, and 6 groups of subsequent atoms, and define the CG beads as the average over each group of atoms. It is worth noting that our definition of possible mappings is different from what is considered in ref (43). There, the authors define a valid mapping as a partitioning of all the 40 Cα’s of protein 2ERL into N = 2, 4, 5, 8, 10, 20 disjoint groups of an equal number of 40/N Cα atoms. They require the Cα atoms belonging to the same CG bead to be connected in the GNM but not necessarily to be subsequent along the sequence. This criterion generates quite a large number of possible mappings, e.g., for N = 5 there exist ∼1024 choices. For this reason, they sample the landscape of allowed CG mappings with Monte Carlo simulations. In contrast to ref (43), in the present work we require the CG beads to be formed by groups of subsequent atoms, while we also consider partitions of atoms into groups of different sizes, ranging from 1 to 40–(N–1). This definition of possible mappings allows us to exhaustively enumerate them. For instance, for N = 5 there exist 82251 combinations. A more detailed comparison of the results obtained with the mapping choice of ref (43) is presented in the Supporting Information.
At each resolution, we evaluate the analytical expression for the VAMP score, the Vibrational Power, and Smap (see Methods and Supporting Information for details) over all the possible CG mappings and select the ones optimizing the different metrics. Because of the large number of possible CG mappings for this system, the training of an autoencoder for a numerical estimate of the reconstruction error for each of them is not feasible and we limit the analysis to these three metrics that can be analytically evaluated. Figure 3A shows the grouping of consecutive Cα atoms to CG beads by different colors. Groups consisting of single Cα’s are shown as a sphere. It is clear that different mapping criteria lead to significantly different optimal mapping schemes. Analogously to the 4-bead harmonic system discussed above, the maximization of the Vibrational Power tends to select N – 1 single Cα atoms at the termini as CG beads while grouping all the remaining 40 – (N – 1) Cα atoms into a single bead. This effect is seen at all resolutions considered (see Figure 3A). Indeed, this selection is consistent with the preservation of the largest amplitude of motion, corresponding to the displacements of the termini of the protein with respect to each other. On the other hand, the optimization of the Smap yields CG mappings corresponding to more uniform partitions of atoms along the sequence, consistent with the preservation of local and high-frequency motions. The CG mappings selected by the maximization of the VAMP score is a sort of compromise between the grouping selected according to the optimization of the Smap or Vibrational Power metrics, as it comprises a combination of single atoms at the termini and different stretches of atoms across the protein.
Figure 3.
(A) Comparison of the optimal mappings for the GNM of protein 2ERL at different bead resolutions. The CG mappings optimizing the VAMP/Variational Power/mapping entropy (top/middle/bottom) criteria (refer to text for details). Different resolutions are shown from the left (2 CG beads) to the right (6 CG beads). (B) VAMP score corresponding to each possible mapping strategy at 4-bead resolution plotted versus the corresponding Vibrational Power. The gray lines running along the top and right indicate the optimal mappings for the two strategies. The colored dots indicate the models corresponding to different optimal mapping strategies, and the orange diamond correspond to the block map, with all beads composed of the same number of atoms. (C) Time scales of the system (as obtained by TICA) ordered by decreasing value for the three different mapping strategies (indicated by the colors) for a model with a 4-bead resolution, in comparison to the full-resolution model.
We note the optimal mappings for the Smap or Vibrational Power metrics shown in Figure 3 are very different from those reported in ref,43 as there the CG beads are constrained to contain the same number of Cα atoms and the nonhomogeneous bead sizes obtained here are a priori excluded.
In Figure 3B, the VAMP score corresponding to all possible 4 bead resolution CG mappings is plotted versus the Vibrational Power, and the CG optimal mappings according to different criteria are highlighted.
Figure 3C shows that VAMP-based CG maps best preserve the long time scale dynamics. The time scales are estimated from the eigenvalues of the Koopman matrix defined by the covariance and time-lagged covariance of the coordinates of the CG beads, as customary in the analysis of MD simulation (see Supporting Information and ref (53) for additional detail). The time scales are reported in order of decreasing value for the different optimal mapping choices at resolution N = 4 and compared with the time scales estimated by the same method on the full resolution (i.e., N = 40). Based on the definition of the GNM energy function (eq 6), if a resolution of 4 beads is chosen for the CG system, we can compare only the three slowest time scales of the full resolution GNM with the time scales reproduced by the different CG systems. The CG mapping selected by the optimization of the VAMP score reproduces accurately the first three time scales, significantly better than the ones selected by the optimization of the Vibrational Power or of Smap. The orange diamonds in Figure 3, parts B and C, mark the values corresponding to the block map, that is the CG map where each bead contains the same number of atoms. This map is very close to the one optimizing the Vibrational Power when the mapping space is defined by the criterion of ref (43) (see Supporting Information for a detailed comparison with the results obtained with this criterion).
Model Protein System
Finally, we turn to a more realistic
albeit simple system: a 13-atom model protein containing harmonic
bonds/angles and nonbonded interactions via Lennard-Jones potentials
(Figure 1C). This system
was originally proposed in ref,48 and shown
to exhibit folding/unfolding dynamics. For increased interpretability
and for fast computation, we focus here only on the slicing strategy
for the definition of the CG mappings, and at the fixed resolution
of N = 5 CG beads, considering all 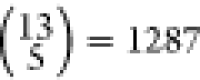 ways of selecting 5 beads from the 13 “atoms”
of the model. Because of the nontrivial interactions, we cannot obtain
analytical resolutions for this system, however, the VAMP score and
Vibrational Power can be computed numerically by estimating the covariance
and time-lagged covariance matrices over simulated trajectories47 (see Supporting Information). For every mapping, we assume that the corresponding effective
CG energy function is thermodynamically consistent with the reference
fine-grained model. This implies that the CG model can reproduce the
same probability distribution for the CG degrees of freedom as obtained
from the high-resolution trajectories under the CG mapping. With these premises, we can use the high-resolution
trajectory directly to compute ensemble averages.
ways of selecting 5 beads from the 13 “atoms”
of the model. Because of the nontrivial interactions, we cannot obtain
analytical resolutions for this system, however, the VAMP score and
Vibrational Power can be computed numerically by estimating the covariance
and time-lagged covariance matrices over simulated trajectories47 (see Supporting Information). For every mapping, we assume that the corresponding effective
CG energy function is thermodynamically consistent with the reference
fine-grained model. This implies that the CG model can reproduce the
same probability distribution for the CG degrees of freedom as obtained
from the high-resolution trajectories under the CG mapping. With these premises, we can use the high-resolution
trajectory directly to compute ensemble averages.
The relatively small number of CG mapping choices allows training a separate autoencoder for each mapping in order to evaluate the corresponding reconstruction error, whereas values of Smap cannot be as simply estimated and associated with the different mappings for this system. A numerical approximation for Smap does exist;40 however, some ambiguity remains on the definition of the appropriate choice of parameters for this method. We found the results to vary wildly with small variations of these parameters. Additionally, as it was already discussed in ref (43), and as is evident from the results presented above, it is clear that Smap does not provide useful information on the preservation of slow degrees of freedom upon coarse-graining.
Figure 4a shows the Vibrational Power corresponding to each of the different CG mappings, plotted as a function of the VAMP score for the same mapping. The two quantities weakly correlate in the area corresponding to poor choices of CG mapping, indicated by small values of both. However, the CG mappings selected by the optimization of these two metrics (gray horizontal and vertical lines for the Vibrational Power and VAMP score, respectively, and illustrated on a cartoon of the protein model) are significantly different: a maximum Vibrational Power select the atoms at the terminal ends as CG beads, while a maximum VAMP score disperses them evenly throughout the model protein. As for the previous systems, these results are in agreement with the interpretation of the VP metric capturing the largest amplitude displacements of the system, but failing to recover the more nuanced motion involving degrees of freedom along the hairpin. The CG mapping corresponding to a minimal reconstruction error is also highlighted in the plot and illustrated on the protein model.
Figure 4.
Top panel: The VAMP score corresponding to all possible 5 bead resolutions CG mappings for the model protein is plotted versus the Vibrational Power. The gray lines running along the top and right indicate the optimal mappings for the two strategies. For each optimal mapping, the corresponding CG model is shown with the selected beads highlighted. Bottom panel: Projection of the TICA time scales for CG models corresponding to different optimal mapping strategies (colored dots), compared to the TICA time scales of the full-resolution model (gray dots).
As in the previous example, Figure 4b shows the model protein’s relaxation time scales recovered by different CG mappings. The time scales are approximated using the TICA method,65 by computing the Koopman matrix using covariance matrices of all interparticle distances (see Supporting Information for details). The 6 slowest time scales associated with the CG mapping with optimal VAMP score (4b, blue dots) closely match the time scales of the 6 slowest time scales of the full resolution model (gray dots). Additionally, even faster time scales (index >6) are reproduced to a good degree. The CG mapping with maximum Vibrational Power reproduces the 6 slowest time scales to a lesser extent, and presents a sharp drop for time scales with an index >6, again indicating that this metric does not necessarily preserve the system dynamics. This gives evidence that, for this system coarse-grained at a 5-bead resolution, the optimization of the Vibrational Power captures well the longest-time scale behavior of the system corresponding to the fluctuations of the end-to-end distance, but it cannot recover additional slow processes. The results associated with the CG mapping corresponding to the minimization of the reconstruction error appear to lay in between what is obtained with the other two metrics.
It is important to note that, if different or additional properties are desired in a CG model (instead or in addition to recovery of the slow dynamics), e.g., the possibility of accurately backmapping to the full resolution, one needs to change the optimization metric or find a compromise between two or more optimization criteria. While the maximization of the mapping entropy appears to produce mappings very different from the optimization of the other metrics in all the examples presented here (see, e.g., Figure 2), from Figure 4, it appears that there is no strong trade-off between the minimization of the reconstruction error and the maximization of the VAMP score, at least for this simple model system.
Conclusion
We explore the definition of an optimal CG mapping scheme and consider a variety of methods based on information theory, structural reconstruction, or Koopman theory for dynamical systems. We do this under the assumption that coarse-graining can be split into two separate processes: (1) choice of mapping and (2) definition of a CG Hamiltonian. Here we focus on the choice of mapping to build CG models with a well-defined main objective and use the thermodynamic consistency criterion for bottom-up coarse-graining18 to define the corresponding CG Hamiltonian (eq 1). While this assumption is justified for the simple models used in this work, in a more realistic setting the choice of the mapping is of course interconnected with the design of the CG energy function. In biological and soft matter systems, we argue that the main objective of coarse-graining is to be able to correctly capture the behavior of a complex and high-dimensional system over long time scales. That is, we want a coarse-grained model to simulate the time scales where most physically relevant processes such as global protein conformational changes or ligand binding/unbinding occur, but they are challenging to characterize with fine-grained simulations. The faster degrees of freedom in contrast, which may be potentially relevant for, e.g., biochemical specificity, are amenable to be probed with all-atom simulations at a reasonable computational cost. Following this line of reasoning, a suitable bottom-up coarse-grained model should be able to accurately recover the appropriate slow mechanisms and describe the transitions between the same metastable states as accurately as the all-atom counterpart. As the preservation of the slowest processes upon coarse-graining is of key importance, a mapping scheme optimized toward this goal is usually desirable.
In the field of dynamical systems and Koopman theory, the VAMP score has been introduced to quantify the ability of a (small) set of features to capture the slow “dynamical modes” of a system, and we propose here to use this metric also for the definition of an optimal CG mapping. Loosely speaking, a choice of coordinates based on the maximization of the VAMP score leads to the selection of the subset of degrees of freedom that more accurately spans the space defined by the first few eigenfunctions of the Koopman operator, that in turn provides the best linear approximation of the system’s dynamic evolution.47
It is important to note that, for realistic systems, in order to accurately recover the dynamics of the fine-grained system in the CG coordinates, one would need to use a generalized Langevin equation, derived, e.g., through the Mori–Zwanzig formalism and comprising a memory kernel. However, building up on previous work,66,67 we have recently shown68 that for overdamped Langevin dynamics, if the eigenfunctions of the Koopman operator of the fine-grained system can be well approximated in the space spanned by the CG coordinates, the corresponding time scales are also well approximated by the projected CG dynamics in the form of an overdamped Langevin equation. As the maximization of the VAMP score selects the CG coordinates that best approximate the fine-grained eigenfunctions, the maximization of the VAMP score is consistent with this point of view.
We have tested this idea by comparing the performance of a CG mapping scheme maximizing the VAMP score against other popular choices, on three different systems of increasing complexity, by means of both analytical and numerical calculations. We show that, while the optimization of the VAMP score leads to the successful recovery of the dynamics on the slowest time scales, alternative methods fall short in this regard.
On the basis of these results, we believe that the definition of CG mapping to preserve molecular kinetics can be done systematically. Here we have shown a proof of principle on simple model systems, but the same criterion could be used for the choice of resolution in a more realistic CG protein model transferable in sequence space. That means that different partitioning of the atoms in each amino acid into CG beads could be explored and compared. For instance how much more kinetic information is preserved if a Cα–Cβ CG model is used instead of a Cα-only model on a set of test proteins? Future work will address this question and related ones.
In this regard, we want to emphasize that the choice of mapping is only the first step in constructing a complete CG model and the overall performance of the model critically depends on the definition of the CG Hamiltonian as well. Nevertheless, we believe that the optimization of the CG resolution plays an important role in the ability of the model to reproduce the system’s long-time scale behavior.
Methods
Simulation Protocol
Numerical simulations for the harmonic systems were carried out following the protocol outlined in ref (69) and are summarized in the Supporting Information.
Coarse-Graining of a Harmonic Model
We consider a general harmonic system with an energy function in the form
| 6 |
where Γ is the connectivity matrix (called Kirchhoff matrix in the context of a GNM), x is the vector of all coordinates, x0 is the vector of coordinates of a reference configuration, and δx is the displacement vector.
By following ref (39), the full thermodynamics of a harmonic system can be obtained, as well as for CG models thermodynamically consistent with it. Here we report the definitions and final analytical expressions; for a full derivation please refer to refs (39 and 43).
We assume a linear mapping 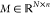 defines the coarse-grained
coordinates
defines the coarse-grained
coordinates 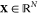 from the fine-grained
ones
from the fine-grained
ones  : X = Mx, with N ≪ n. eq 1 reports
the general definition
of the effective CG energy function, W(X), that is thermodynamically consistent with a fine-grained model
with energy u(x).18 For a harmonic system with energy given by eq 6, a compact solution for the expression
of the thermodynamically consistent CG energy (eq 1) can be obtained analytically:
: X = Mx, with N ≪ n. eq 1 reports
the general definition
of the effective CG energy function, W(X), that is thermodynamically consistent with a fine-grained model
with energy u(x).18 For a harmonic system with energy given by eq 6, a compact solution for the expression
of the thermodynamically consistent CG energy (eq 1) can be obtained analytically:
| 7 |
where W0 is a protein-independent constant, δX = X – X0 is the vector of the displacements in the coordinates of the CG beads, X0 = Mx0 is the reference configuration of the CG model, and we have defined the effective CG matrix K as
| 8 |
where Q = 1N – 1/NJNJNT is
the projection operator that filters out free translations and the
vector 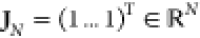 . In eq 7
. In eq 7
| 9 |
and
| 10 |
are the products of the nonzero eigenvalues of the matrix Γ and K, respectively.
Mapping Entropy
Following ref (39), the mapping entropy associated with a CG model is given by the difference between the excess configurational entropy of the full resolution model, sr, and the same quantity when it is “perceived” from the CG configurational space, sR:
| 11 |
| 12 |
| 13 |
where V is the volume of the system, and px(x) and pX(X) are the Boltzmann weights associated with the energy function of eq 6 and of eq 7, respectively. The mapping entropy Smap is always negative and its maximization (that is, the minimization of its absolute value) has been proposed as a criterion to define an optimal CG map.39
For a harmonic system, these expressions can be analytically evaluated,39,43 and they give
| 14 |
| 15 |
| 16 |
where both s0 and C(N, n) are model-independent constants (s0 is only function of the volume, and C(N, n) depends on the dimensionality of the fine-grained and coarse-grained models), and tΓ, TK are the products of the nonzero eigenvalues, λi and Λi of the matrices Γ and K, respectively (see eqs 9 and 10)).
As the eigenvalues λi and Λi are all positive, the expression for the mapping entropy (16) can also be written as
| 17 |
| 18 |
| 19 |
where we have used C00 = K–1 and defining c00 = Γ–1.
VAMP Score for Harmonic Systems
Here we provide a quick overview of the procedure and provide the final result for the analytical calculation of the VAMP score in a system of beads connected by harmonic springs, with energy in the form of eq 6. For the full derivation please refer to the Supporting Information.
From its definition (eq 2), the calculation of the VAMP score requires the evaluation of the matrices C00 and C0τ (eqs 3 and 4). These matrices can be computed analytically for a harmonic system. The matrix C00 represents the covariance of the CG coordinates and is straightforwardly obtained as
| 20 |
where K is the effective CG matrix defined in eq 8. The matrix C0τ is the time-lagged covariance matrix, that can be expressed as
| 21 |
where 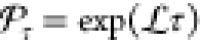 is the propagator of the
dynamics associated with the (full resolution) harmonic system, for
a lagtime τ, and
is the propagator of the
dynamics associated with the (full resolution) harmonic system, for
a lagtime τ, and 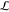 is the generator of the
dynamics.13 Assuming that the time evolution
of the system can be described as an overdamped Langevin dynamics,
with friction coefficient γ, the eingenfunctions and eigenvectors
of the dynamic propagator can be obtained. Therefore, by decomposing
the system coordinates into these eigenfunctions, expression 21 can be analytically evaluated
(see Supporting Information for details).
The final result is
is the generator of the
dynamics.13 Assuming that the time evolution
of the system can be described as an overdamped Langevin dynamics,
with friction coefficient γ, the eingenfunctions and eigenvectors
of the dynamic propagator can be obtained. Therefore, by decomposing
the system coordinates into these eigenfunctions, expression 21 can be analytically evaluated
(see Supporting Information for details).
The final result is
| 22 |
where the matrix Ωτ is defined as
| 23 |
where λi and ui are the eigenvalues and eigenvectors of the matrix Γ. With the expressions for C00 and C0τ, the VAMP score is obtained as
| 24 |
| 25 |
Vibrational Power
Following ref (43), the vibrational power is defined as the trace of the mass-weighted covariance matrix describing correlated fluctuations. Here we assume uniform mass for all particles, and therefore, in our notation, the vibrational power (VP) of a CG model defined by the CG mapping M is
| 26 |
Reconstruction Error
The reconstruction error (RE) is defined as the mean square error (MSE) between the original coordinates of a fine-grained configuration and the reconstructed fine-grained coordinates of the corresponding CG configuration:
| 27 |
Here xi indicates the original fine-grained coordinates of atom i and xi′ the reconstructed fine-grained coordinates. As detailed in the Supporting Information, the reconstruction of the fine-grained coordinates from a CG configuration is obtained by means of an autoencoder, where the encoder part is defined by the CG mapping and the decoder part is trained on long equilibrium simulations of the fine-grained model.
Acknowledgments
The authors gratefully acknowledge financial support from the Deutsche Forschungsgemeinschaft DFG (SFB/TRR 186, Project A12; SFB 1114, Projects B03 and A04; SFB 1078, Project C7; and RTG 2433, Project Q05), the National Science Foundation (CHE-1900374 and PHY-2019745), and the Einstein Foundation Berlin (Project 0420815101). We also thank the members of the Clementi and Noé groups for their helpful discussions. The idea for this study emerged from discussions during the program “Machine learning for physics and the physics of learning” that was held at the Institute for Pure and Applied Mathematics (IPAM) at UCLA in the Fall of 2019. We thank all the participants in the program for the useful and inspiring discussions. C. Clementi and F. Noé would like to acknowledge support from IPAM and the Simons Foundation as Simons Participants.
Data Availability Statement
Simulation data and the code to reproduce the analysis and the plots shown in the manuscript are accessible at https://github.com/ClementiGroup/cg-mapping.git.
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acscentsci.2c01200.
The authors declare no competing financial interest.
Supplementary Material
References
- Shaw D. E.; et al. Anton, a special-purpose machine for molecular dynamics simulation. Commun. ACM 2008, 51, 91–97. 10.1145/1364782.1364802. [DOI] [Google Scholar]
- Laio A.; Parrinello M. Escaping free-energy minima. Proc. Natl. Acad. Sci. U.S.A. 2002, 99, 12562–12566. 10.1073/pnas.202427399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dellago C.; Bolhuis P. G.; Csajka F. S.; Chandler D. Transition path sampling and the calculation of rate constants. J. Chem. Phys. 1998, 108, 1964–1977. 10.1063/1.475562. [DOI] [Google Scholar]
- Prinz J.-H.; Wu H.; Sarich M.; Keller B. G.; Senne M.; Held M.; Chodera J. D.; Schütte C.; Noé F. Markov models of molecular kinetics: Generation and Validation. J. Chem. Phys. 2011, 134, 174105. 10.1063/1.3565032. [DOI] [PubMed] [Google Scholar]
- Lindorff-Larsen K.; Piana S.; Dror R. O.; Shaw D. E. How Fast-Folding Proteins Fold. Science 2011, 334, 517–520. 10.1126/science.1208351. [DOI] [PubMed] [Google Scholar]
- Voelz V. A.; Bowman G. R.; Beauchamp K.; Pande V. S. Molecular Simulation of ab Initio Protein Folding for a Millisecond Folder NTL9(1–39). J. Am. Chem. Soc. 2010, 132, 1526–1528. 10.1021/ja9090353. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Plattner N.; Doerr S.; De Fabritiis G.; Noé F. Complete protein–protein association kinetics in atomic detail revealed by molecular dynamics simulations and Markov modelling. Nat. Chem. 2017, 9, 1005–1011. 10.1038/nchem.2785. [DOI] [PubMed] [Google Scholar]
- Schütte C.; Sarich M.. Metastability and Markov state models in molecular dynamics: modeling, analysis, algorithmic approaches; Current lecture notes in mathematics; American Mathematical Society: Providence, RI, 2013; Vol. 24, p 15; 10.1090/cln/024/03 [DOI] [Google Scholar]
- Clementi C. Coarse-grained models of protein folding: toy models or predictive tools?. Curr. Opin. Struct. Biol. 2008, 18, 10–15. 10.1016/j.sbi.2007.10.005. [DOI] [PubMed] [Google Scholar]
- Clementi C.; Nymeyer H.; Onuchic J. N. Topological and energetic factors: what determines the structural details of the transition state ensemble and “en-route” intermediates for protein folding? An investigation for small globular proteins. J. Mol. Biol. 2000, 298, 937–953. 10.1006/jmbi.2000.3693. [DOI] [PubMed] [Google Scholar]
- Kmiecik S.; Gront D.; Kolinski M.; Wieteska L.; Dawid A. E.; Kolinski A. Coarse-Grained Protein Models and Their Applications. Chem. Rev. 2016, 116, 7898–7936. 10.1021/acs.chemrev.6b00163. [DOI] [PubMed] [Google Scholar]
- Onuchic J. N.; Luthey-Schulten Z.; Wolynes P. G. THEORY OF PROTEIN FOLDING: The Energy Landscape Perspective. Annu. Rev. Phys. Chem. 1997, 48, 545–600. 10.1146/annurev.physchem.48.1.545. [DOI] [PubMed] [Google Scholar]
- Schütte C.; Fischer A.; Huisinga W.; Deuflhard P. A Direct Approach to Conformational Dynamics based on Hybrid Monte Carlo. J. Comput. Phys. 1999, 151, 146–168. 10.1006/jcph.1999.6231. [DOI] [Google Scholar]
- Pande V. S.; Beauchamp K.; Bowman G. R. Everything you wanted to know about Markov State Models but were afraid to ask. Methods 2010, 52, 99–105. 10.1016/j.ymeth.2010.06.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Levitt M.; Warshel A. Computer simulation of protein folding. Nature 1975, 253, 694–698. 10.1038/253694a0. [DOI] [PubMed] [Google Scholar]
- Davtyan A.; Schafer N. P.; Zheng W.; Clementi C.; Wolynes P. G.; Papoian G. A. AWSEM-MD: Protein Structure Prediction Using Coarse-Grained Physical Potentials and Bioinformatically Based Local Structure Biasing. J. Phys. Chem. B 2012, 116, 8494–8503. 10.1021/jp212541y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Noid W. G. Perspective: Coarse-grained models for biomolecular systems. J. Chem. Phys. 2013, 139, 090901. 10.1063/1.4818908. [DOI] [PubMed] [Google Scholar]
- Noid W. G.; Chu J.-W.; Ayton G. S.; Krishna V.; Izvekov S.; Voth G. A.; Das A.; Andersen H. C. The multiscale coarse-graining method. I. A rigorous bridge between atomistic and coarse-grained models. J. Chem. Phys. 2008, 128, 244114. 10.1063/1.2938860. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shell M. S. The relative entropy is fundamental to multiscale and inverse thermodynamic problems. J. Chem. Phys. 2008, 129, 144108. 10.1063/1.2992060. [DOI] [PubMed] [Google Scholar]
- Reith D.; Pütz M.; Müller-Plathe F. Deriving effective mesoscale potentials from atomistic simulations: Mesoscale Potentials from Atomistic Simulations. J. Comput. Chem. 2003, 24, 1624–1636. 10.1002/jcc.10307. [DOI] [PubMed] [Google Scholar]
- Marrink S. J.; Risselada H. J.; Yefimov S.; Tieleman D. P.; de Vries A. H. The MARTINI Force Field: Coarse Grained Model for Biomolecular Simulations. J. Phys. Chem. B 2007, 111, 7812–7824. 10.1021/jp071097f. [DOI] [PubMed] [Google Scholar]
- Bereau T.; Deserno M. Generic coarse-grained model for protein folding and aggregation. J. Chem. Phys. 2009, 130, 235106. 10.1063/1.3152842. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang J.; Olsson S.; Wehmeyer C.; Peŕez A.; Charron N. E.; De Fabritiis G.; Noe F.; Clementi C. Machine Learning of coarse-grained Molecular Dynamics Force Fields. ACS Cent. Sci. 2019, 5, 755–767. 10.1021/acscentsci.8b00913. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang L.; Han J.; Wang H.; Car R.; E W. DeePCG: Constructing coarse-grained models via deep neural networks. J. Chem. Phys. 2018, 149, 034101. 10.1063/1.5027645. [DOI] [PubMed] [Google Scholar]
- Wang W.; Gómez-Bombarelli R. Coarse-graining auto-encoders for molecular dynamics. NPJ. Comput. Mater. 2019, 5, 125. 10.1038/s41524-019-0261-5. [DOI] [Google Scholar]
- Husic B. E.; Charron N. E.; Lemm D.; Wang J.; Peŕez A.; Krämer A.; Chen Y.; Olsson S.; De Fabritiis G.; Noé F.; Clementi C.; et al. Coarse graining molecular dynamics with Graph Neural Networks. J. Chem. Phys. 2020, 153, 194101. 10.1063/5.0026133. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Köhler J.; Chen Y.; Krämer A.; Clementi C.; Noé F.. Force-matching Coarse-Graining without Forces. arXiv 2022; 2203.11167.
- Chen Y.; Krämer A.; Charron N. E.; Husic B. E.; Clementi C.; Noé F. Machine learning implicit solvation for molecular dynamics. J. Chem. Phys. 2021, 155, 084101. 10.1063/5.0059915. [DOI] [PubMed] [Google Scholar]
- Wang J.; Charron N.; Husic B.; Olsson S.; Noé F.; Clementi C. Multi-body effects in a coarse-grained protein force field. J. Chem. Phys. 2021, 154, 164113. 10.1063/5.0041022. [DOI] [PubMed] [Google Scholar]
- Koehl P.; Poitevin F.; Navaza R.; Delarue M. The Renormalization Group and Its Applications to Generating Coarse-Grained Models of Large Biological Molecular Systems. J. Chem. Theory Comput. 2017, 13, 1424–1438. 10.1021/acs.jctc.6b01136. [DOI] [PubMed] [Google Scholar]
- Diggins P.; Liu C.; Deserno M.; Potestio R. Optimal Coarse-Grained Site Selection in Elastic Network Models of Biomolecules. J. Chem. Theory Comput. 2019, 15, 648–664. 10.1021/acs.jctc.8b00654. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rudzinski J. F.; Noid W. G. Investigation of Coarse-Grained Mappings via an Iterative Generalized Yvon–Born–Green Method. J. Phys. Chem. B 2014, 118, 8295–8312. 10.1021/jp501694z. [DOI] [PubMed] [Google Scholar]
- Dallavalle M.; van der Vegt N. F. A. Evaluation of mapping schemes for systematic coarse graining of higher alkanes. Phys. Chem. Chem. Phys. 2017, 19, 23034–23042. 10.1039/C7CP03926C. [DOI] [PubMed] [Google Scholar]
- Zavadlav J.; Arampatzis G.; Koumoutsakos P. Bayesian selection for coarse-grained models of liquid water. Sci. Rep. 2019, 9, 99. 10.1038/s41598-018-37471-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jin J.; Pak A. J.; Voth G. A. Understanding Missing Entropy in Coarse-Grained Systems: Addressing Issues of Representability and Transferability. J. Phys. Chem. Lett. 2019, 10, 4549–4557. 10.1021/acs.jpclett.9b01228. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chakraborty M.; Xu J.; White A. D. Is preservation of symmetry necessary for coarse-graining?. Phys. Chem. Chem. Phys. 2020, 22, 14998–15005. 10.1039/D0CP02309D. [DOI] [PubMed] [Google Scholar]
- Bernhardt M. P.; Dallavalle M.; Van der Vegt N. F. A. Application of the 2PT model to understanding entropy change in molecular coarse-graining. Soft Mater. 2020, 18, 274–289. 10.1080/1539445X.2020.1737118. [DOI] [Google Scholar]
- LeCun Y.; Chopra S.; Hadsell R.; Ranzato M.; Huang F. J.. PREDICTING STRUCTURED DATA; MIT Press: 2007. [Google Scholar]
- Foley T. T.; Shell M. S.; Noid W. G. The impact of resolution upon entropy and information in coarse-grained models. J. Chem. Phys. 2015, 143, 243104. 10.1063/1.4929836. [DOI] [PubMed] [Google Scholar]
- Giulini M.; Menichetti R.; Shell M. S.; Potestio R. An Information-Theory-Based Approach for Optimal Model Reduction of Biomolecules. J. Chem. Theory Comput. 2020, 16, 6795–6813. 10.1021/acs.jctc.0c00676. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Errica F.; Giulini M.; Bacciu D.; Menichetti R.; Micheli A.; Potestio R. A Deep Graph Network-Enhanced Sampling Approach to Efficiently Explore the Space of Reduced Representations of Proteins. Front. Mol. Biosci. 2021, 8, 637396. 10.3389/fmolb.2021.637396. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Menichetti R.; Giulini M.; Potestio R. A journey through mapping space: characterising the statistical and metric properties of reduced representations of macromolecules. Eur. Phys. J. B 2021, 94, 204. 10.1140/epjb/s10051-021-00205-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Foley T. T.; Kidder K. M.; Shell M. S.; Noid W. G. Exploring the landscape of model representations. Proc. Natl. Acad. Sci. U.S.A. 2020, 117, 24061–24068. 10.1073/pnas.2000098117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chakraborty M.; Xu C.; White A. D. Encoding and selecting coarse-grain mapping operators with hierarchical graphs. J. Chem. Phys. 2018, 149, 134106. 10.1063/1.5040114. [DOI] [PubMed] [Google Scholar]
- Webb M. A.; Delannoy J.-Y.; de Pablo J. J. Graph-Based Approach to Systematic Molecular Coarse-Graining. J. Chem. Theory Comput. 2019, 15, 1199–1208. 10.1021/acs.jctc.8b00920. [DOI] [PubMed] [Google Scholar]
- Li Z.; Wellawatte G. P.; Chakraborty M.; Gandhi H. A.; Xu C.; White A. D. Graph neural network based coarse-grained mapping prediction. Chem. Sci. 2020, 11, 9524–9531. 10.1039/D0SC02458A. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu H.; Noé F. Variational Approach for Learning Markov Processes from Time Series Data. J. Nonlinear Sci. 2020, 30, 23–66. 10.1007/s00332-019-09567-y. [DOI] [Google Scholar]
- Mendels D.; de Pablo J. J. Collective Variables for Free Energy Surface Tailoring: Understanding and Modifying Functionality in Systems Dominated by Rare Events. J. Phys. Chem. Lett. 2022, 13, 2830–2837. 10.1021/acs.jpclett.2c00317. [DOI] [PubMed] [Google Scholar]
- Noé F.; Clementi C. Collective variables for the study of long-time kinetics from molecular trajectories: theory and methods. Curr. Opin. Struct. Biol. 2017, 43, 141–147. 10.1016/j.sbi.2017.02.006. [DOI] [PubMed] [Google Scholar]
- Noé F.; Nüske F. A Variational Approach to Modeling Slow Processes in Stochastic Dynamical Systems. Multiscale Model. Simul. 2013, 11, 635–655. 10.1137/110858616. [DOI] [Google Scholar]
- Nüske F.; Keller B. G.; Pérez-Hernández G.; Mey A. S. J. S.; Noé F. Variational Approach to Molecular Kinetics. J. Chem. Theory Comput. 2014, 10, 1739–1752. 10.1021/ct4009156. [DOI] [PubMed] [Google Scholar]
- Molgedey L.; Schuster H. G. Separation of a mixture of independent signals using time delayed correlations. Phys. Rev. Lett. 1994, 72, 3634–3637. 10.1103/PhysRevLett.72.3634. [DOI] [PubMed] [Google Scholar]
- Pérez-Hernández G.; Paul F.; Giorgino T.; De Fabritiis G.; Noé F. Identification of slow molecular order parameters for Markov model construction. J. Chem. Phys. 2013, 139, 015102. 10.1063/1.4811489. [DOI] [PubMed] [Google Scholar]
- Mardt A.; Pasquali L.; Wu H.; Noé F. VAMPnets for deep learning of molecular kinetics. Nat. Commun. 2018, 9, 5. 10.1038/s41467-017-02388-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen W.; Tan A. R.; Ferguson A. L. Collective variable discovery and enhanced sampling using autoencoders: Innovations in network architecture and error function design. J. Chem. Phys. 2018, 149, 072312. 10.1063/1.5023804. [DOI] [PubMed] [Google Scholar]
- Bonati L.; Piccini G.; Parrinello M. Deep learning the slow modes for rare events sampling. Proc. Natl. Acad. Sci. U.S.A. 2021, 118, e2113533118. 10.1073/pnas.2113533118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koopman B. O. Hamiltonian Systems and Transformation in Hilbert Space. Proc. Natl. Acad. Sci. U.S.A. 1931, 17, 315–318. 10.1073/pnas.17.5.315. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mezić I. Spectral Properties of Dynamical Systems, Model Reduction and Decompositions. Nonlinear Dyn. 2005, 41, 309–325. 10.1007/s11071-005-2824-x. [DOI] [Google Scholar]
- Korda M.; Mezić I. On Convergence of Extended Dynamic Mode Decomposition to the Koopman Operator. J. Nonlinear Sci. 2018, 28, 687–710. 10.1007/s00332-017-9423-0. [DOI] [Google Scholar]
- Scherer M. K.; Husic B. E.; Hoffmann M.; Paul F.; Wu H.; Noé F. Variational selection of features for molecular kinetics. J. Chem. Phys. 2019, 150, 194108. 10.1063/1.5083040. [DOI] [PubMed] [Google Scholar]
- Müller-Plathe F. Coarse-Graining in Polymer Simulation: From the Atomistic to the Mesoscopic Scale and Back. ChemPhysChem 2002, 3, 754–769. . [DOI] [PubMed] [Google Scholar]
- Bahar I.; Atilgan A. R.; Erman B. Direct evaluation of thermal fluctuations in proteins using a single-parameter harmonic potential. Fold Des. 1997, 2, 173–181. 10.1016/S1359-0278(97)00024-2. [DOI] [PubMed] [Google Scholar]
- Bahar I.; Atilgan A. R.; Demirel M. C.; Erman B. Vibrational Dynamics of Folded Proteins: Significance of Slow and Fast Motions in Relation to Function and Stability. Phys. Rev. Lett. 1998, 80, 2733–2736. 10.1103/PhysRevLett.80.2733. [DOI] [Google Scholar]
- Tirion M. M. Large Amplitude Elastic Motions in Proteins from a Single-Parameter, Atomic Analysis. Phys. Rev. Lett. 1996, 77, 1905–1908. 10.1103/PhysRevLett.77.1905. [DOI] [PubMed] [Google Scholar]
- Naritomi Y.; Fuchigami S. Slow dynamics in protein fluctuations revealed by time-structure based independent component analysis: The case of domain motions. J. Chem. Phys. 2011, 134, 065101. 10.1063/1.3554380. [DOI] [PubMed] [Google Scholar]
- Zhang W.; Hartmann C.; Schütte C. Effective dynamics along given reaction coordinates, and reaction rate theory. Faraday Discuss. 2016, 195, 365–394. 10.1039/C6FD00147E. [DOI] [PubMed] [Google Scholar]
- Zhang W.; Schütte C. Reliable Approximation of Long Relaxation Timescales in Molecular Dynamics. Entropy 2017, 19, 367. 10.3390/e19070367. [DOI] [Google Scholar]
- Nüske F.; Koltai P.; Boninsegna L.; Clementi C. Spectral Properties of Effective Dynamics from Conditional Expectations. Entropy 2021, 23, 134. 10.3390/e23020134. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guttenberg N.; Dama J. F.; Saunders M. G.; Voth G. A.; Weare J.; Dinner A. R. Minimizing memory as an objective for coarse-graining. J. Chem. Phys. 2013, 138, 094111. 10.1063/1.4793313. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Simulation data and the code to reproduce the analysis and the plots shown in the manuscript are accessible at https://github.com/ClementiGroup/cg-mapping.git.






