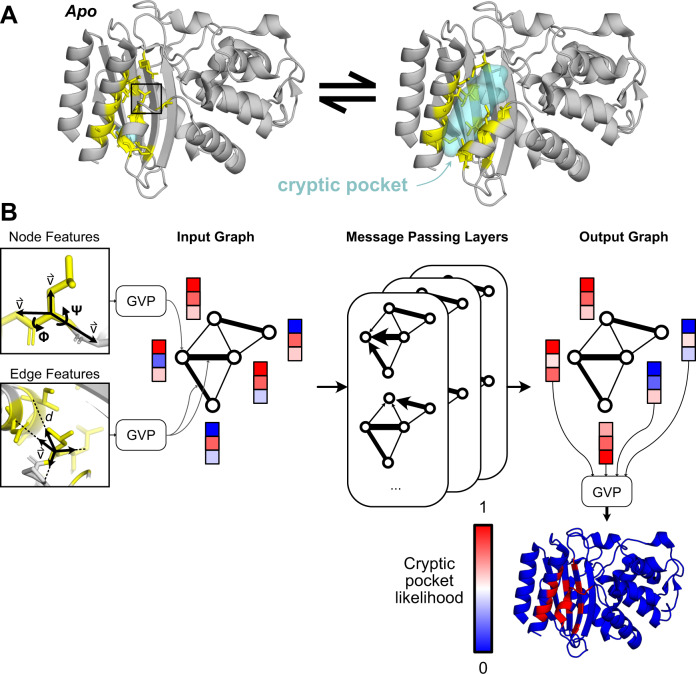
Fig. 1. PocketMiner uses graph neural networks to predict cryptic pocket formation.

A Proteins exist in an equilibrium between different structures, including experimentally derived structures that lack cryptic pockets (left, PDB ID 1JWP)⁷¹ and those with open cryptic pockets (right, PDB ID 1PZO)⁴. Residues lining the cryptic pocket are shown in yellow sticks. B PocketMiner relies on a series of message passing layers to exchange information between residues and to generate encodings that can predict sites of cryptic pocket formation. On the left, we show the structural features that are fed into an input graph following transformations by Geometric Vector Perceptron (GVP) layers. Node features include backbone dihedral angles as well as forward and reverse unit vectors (for a full list see Methods). Edge features include a radial basis encoding of the distance between residues and a unit vector between their alpha-carbons. In the middle, we show how the input graph is transformed by messaging passing layers which influence a residue’s embedding based on its neighbors’ node embeddings as well as its edge embeddings. On the right, we show that the node embeddings from the output graph are used to make predictions of cryptic pocket likelihood following another GVP transformation. Finally, at the bottom right, we show an idealized prediction for the protein shown in A.