Abstract
Objective:
Self-reported energy intake (EI) estimation may incur systematic errors that could be attenuated through biomarker calibration. We aimed to confirm whether calibrated EI was comparable to total energy expenditure (TEE) measured using the doubly labelled water (DLW) technique.
Design:
Cross-sectional study.
Setting:
General older population from the Kyoto–Kameoka Study, Japan.
Participants:
This study included sub- and main cohorts of 72 and 8058 participants aged≥ 65 years, respectively. EI was evaluated using a validated FFQ, and calibrated EI was obtained using a previously developed equation based on the DLW method. TEE was considered representative of true EI and also measured using the DLW method. We used a Wilcoxon signed-rank test and correlation analysis to compare the uncalibrated and calibrated EI with TEE.
Results:
In the sub-cohort, the median TEE, uncalibrated EI and calibrated EI were 8559 kJ, 7088 kJ and 9269 kJ, respectively. The uncalibrated EI was significantly lower than the TEE (median difference = –1847 kJ; interquartile range (IQR): –2785 to –1096), although the calibrated EI was not (median difference = 463 kJ; IQR: –330 to 1541). The uncalibrated (r = 0·275) and calibrated EI (r = 0·517) significantly correlated with TEE. The reproducibility was higher for calibrated EI (interclass correlation coefficient (ICC) = 0·982) than for uncalibrated EI (ICC = 0·637). Similar findings were observed when stratifying the sample by sex. For medians, uncalibrated EI was lower (about 17 %) than calibrated EI in the main cohort.
Conclusions:
Biomarker calibration may improve the accuracy of self-reported dietary intake estimation.
Keywords: Doubly labelled water, FFQ, Energy intake, Validation, Older adults
Diet–disease relationships in nutritional epidemiological studies are dependent on the accuracy of the dietary survey results obtained. Epidemiological studies usually use FFQ, dietary records (DR) or 24-h dietary recalls to assess participants’ habitual dietary habits(1–3). However, dietary assessment methods relying on self-reported data are known for inaccuracies related to the collection and analysis of individuals’ dietary intake information(1,4–7).
Total energy expenditure (TEE) measured using the doubly labelled water (DLW) method is considered an objective biomarker of energy intake (EI) and the gold standard for its estimation in individuals with stable body weight(1,4–10). Previous evidence indicates that compared to TEE determined using the DLW method, DR and 24-h dietary recall underestimate EI by approximately 10–20 %, and FFQ underestimate EI by approximately 20–30 %(6,7). Moreover, underestimation of EI is associated with individual characteristics; data from national surveys demonstrate that age, sex and BMI are associated with underreporting or overreporting of EI in both the USA(11) and Japan(12). Thus, it is difficult to accurately evaluate the EI from self-administered FFQ because of the systematic errors incurred due to participants’ characteristics.
The Strengthening the Reporting of Observational Studies in Epidemiology – Nutritional Epidemiology (STROBE-nut) guidelines recommend using biomarkers to estimate dietary intake(13). Neuhouser et al. reported a new approach involving the use of biomarkers to calibrate systematic errors in EI estimated from self-administered FFQ(5). Calibrated EI, as opposed to non-calibrated EI, is associated with a substantially increased risk of diabetes(14). Therefore, diet–disease associations determined without calibration of self-reported measurement errors should be considered with caution, and information regarding EI imbalance could be useful for disease prevention. To calibrate variables, such as age, sex and weight status, that are associated with misreporting(11,12), we previously developed an equation for EI estimated from an FFQ using the DLW method in Japanese older adults(7). Although this approach may be unable to completely prevent systematic errors, it could lower the systematic errors that occur with self-reported dietary assessment methods to a reasonable level, through regression-based calibration. Moreover, it is important to consider the required sample size for accurate EI estimates(2). However, to our knowledge, the efficacy of the calibration approach for the sample size required for accurate EI estimation has not been evaluated thoroughly. In the present study, we aimed to: (1) evaluate whether the EI estimation is comparable to the TEE measured using the DLW method; (2) to compare the required sample size for accurate EI estimates with and without the calibration approach and (3) compare the uncalibrated and calibrated EI in a large cohort of older adults. We hypothesised that the biomarker calibration approach would improve the accuracy and precision of self-reported EI. The results of this study could help address the biases incurred with self-reporting in dietary assessment methods.
Methods
Study population
The Kyoto–Kameoka Study is a cohort study of older adults aged≥65 years living in Kameoka City, Kyoto Prefecture, Japan. The study details have been explained elsewhere(2,7,15–17). In brief, the cohort participants undertook an FFQ under the Health and Nutrition Status Survey on 14 February 2012(17). The questionnaires were collected by mail and valid responses were received from 8319 participants. Health-related information, including medical history, socio-economic status, smoking habits, height and body weight, was extracted from the mail surveys(17). Of the 8319 respondents, those who self-reported that they needed long-term care (n 136), those with missing data for BMI (n 39) and those for whom estimated EI based on the FFQ was more than three standard deviations higher or lower than the mean value for their sex (n 86) were excluded from the analyses(15). The remainder (n 8058) were included in the study as the main cohort.
From the main cohort, 147 individuals were re-assessed in May–June 2012 for DLW measurement. The details have been explained elsewhere(2,7). Using their data, we previously developed an equation for DLW-calibrated EI(7). Of this sub-cohort, 72 individuals underwent the second assessment for DLW measurement in August 2012. Thus, the sub-cohort comprised 72 individuals. This study was conducted in compliance with the STROBE-nut criteria(13).
Energy intake assessment
The EI was assessed using an FFQ(18,19), which has been previously validated for middle-aged(20) and older adults(2,7). We determined the participants’ average yearly food intake by requesting them to report the frequency at which they consumed the forty-seven food and beverage items included in the FFQ. Fixed portion sizes for each sex were derived from 1-d weighted DR(19). EI was calculated using the programme developed based on the Standard Tables of Food Composition in Japan(21). Spearman’s rank correlation coefficient between the EI derived from the FFQ and those derived from the DR were 0·19 for men and 0·40 for women(2). The EI estimated from FFQ were 10–13 % lower than those estimated from DR for both men and women(2). To confirm the reproducibility, we compared the participants’ EI through another round of FFQ in 14 February 2012 and August 2012.
Calculation of calibrated energy intake
The calibrated EI was calculated using a previously developed equation(7) aimed at attenuating the systematic errors derived from some variables. The EI (estimated using FFQ data) was calibrated via a stepwise multiple regression model using TEE (measured using the DLW technique) as the dependent variable. Age, sex, BMI and EI estimated using FFQ data were included in the model as significant independent variables. The determinant coefficient (R2) of the linear regression analysis was 0·36(7). The models followed the following equation:
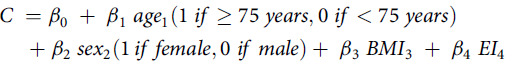 |
In the above equation, C is the calibrated EI. The intercept (β0) was 1384.92 kcal (5795 kJ) in this FFQ. For binary variables, –166.98 kcal (–699 kJ) was the coefficient (β1) for age and – 354.72 kcal (–1484 kJ) was the coefficient (β2) for sex. For continuous variables, the coefficient for BMI (β3) was 25.55 kcal (107 kJ/kg/m2) and that for EI (β4) was 0.24 kcal (1 kJ). This each coefficient was multiplied by a value for the age (1 if≥ 75 years, 0 if < 75 years), sex (1 if female, 0 if male), BMI (continuous) and EI (continuous), and all of the values were summed to obtain a calibrated EI.
BMI was calculated by dividing the self-reported body weight (kg) by the square of the height (m). We previously reported that self-reported BMI did not differ from measured BMI (mean difference: 0.4 kg/m2 in men and 0.5 kg/m2 in women) in this cohort; the Pearson’s correlation coefficient between BMI derived from self-report and those derived from measurement was 0.916 in men and 0.912 in women(16). In addition, the interclass correlation coefficient (ICC) as a measure of the reproducibility of self-reported BMI was 0.910 for men and 0.888 for women(16).
Doubly labelled water
TEE was measured using the DLW method over approximately 2 weeks during May–June 2012 and August 2012. The details have been explained elsewhere(7,22). In brief, we collected the participants’ urine samples before they drank DLW on the morning of day 0 (baseline). Thereafter, the participants drank water containing a premixed dose of 0.12 g/kg estimated total body water of 2H2O (99.9 atom %, Taiyo Nippon Sanso, Tokyo, Japan) and 2.5 g/kg estimated total body water of H218O (10.0 atom %, Taiyo Nippon Sanso, Tokyo, Japan). The urine samples were collected on the morning of days 1, 2, 8, 9, 15 and 16. Concentration of 18O (No) and 2H (Nd) in the urine samples was measured using isotope ratio MS (Hydra 20-20 Stable Isotope Mass Spectrometers; SerCon Ltd, Crewe, UK). The No and Nd dilution spaces were determined by dividing the dose of the administered tracer (as moles of 2H- or 18O-water) using the intercept method at baseline and on days 1, 2, 8, 9, 15 and 16. TEE was calculated using the modified Weir’s equation using the carbon dioxide production rate (rCO2 (mol/d)) and 24-h estimated RER(23). The rCO2 (mol/d) was calculated using the rates of 18O and 2H elimination per d. The RER used for TEE calculation was set at 0.86 for all participants based on previous observations(24). We assumed perfect nourishment balance conditions, which determine that the food quotient has to be equal to the RER(25).
Statistical analysis
Descriptive statistics for categorical variables are expressed as numbers of individuals and percentages. The variables for missing values were supplemented through multivariate imputation from five data sets using the R multivariate imputation by chained equation package(26). All missing values were assumed to be missing at random.
We examined the data for distribution and normality (skewness and kurtosis). The large main cohort data were normally distributed, according to a Jarque–Bera test, and the small sub-cohort data were non-normally distributed, according to a Shapiro–Wilk test (see online Supplemental Fig. 1). To display these variables consistently, the variables such as EI and TEE are shown as median with interquartile range (IQR).
To evaluate the accuracy of the median EI, we used the Wilcoxon signed-rank test to compare the TEE measured by DLW and the uncalibrated and calibrated EI. The ranking of an individual’s EI was evaluated using Spearman’s rank correlation analysis between the TEE and uncalibrated and calibrated EI. Deattenuated correlation coefficients were calculated using Willett’s equation to correct within-person variation in the DLW method that was performed twice (May–June and August 2012)(3). Using the previously established equation(27), we were compared the equivalence of validity of the EI by the correlation coefficients between the uncalibrated and calibrated EI estimated using FFQ data against the TEE. We evaluated the reproducibility of the EI estimated from the FFQ obtained twice using the ICC.
We validated the group and individual mean uncalibrated and calibrated EI, estimated using FFQ data, by using previously reported equations(2). These equations used within-person variance, between-person variance and a ratio of within-person to between-person variance to estimate the required sample size and the appropriate number of survey repetitions. These analyses were also performed after stratifying the sample by sex(2).
In the main cohort, we compared the uncalibrated and calibrated EI and the EI/predicted BMR (pBMR) using the Wilcoxon signed-rank test. The pBMR was estimated using the equation by Ganpule et al. for Japanese individuals(28) given that, in a comparison of several different equations for calculating pBMR, this equation provided the best results(29). EI is predicted to exhibit a negative correlation with age and a positive correlation with BMI and body weight(30). We compared the associations of calibrated and uncalibrated EI with age, body weight and BMI.
For all statistical analyses, the two-sided level of significance was 5 %. All analyses were conducted using JMP Pro for Windows (SAS Institute Inc.) and/or R software 3.4.3 (R Core Team).
Results
Table 1 shows the participants’ characteristics stratified by sex in the cohort. The participants of the sub-cohort, for whom TEE was measured using DLW, tended to be male, alcohol drinkers, and have attained higher education than the remainder of the main cohort; however, these differences were minor.
Table 1.
Comparison of the characteristics of the participants included in the main and sub-cohorts stratified by sex
| Main cohort* | Sub-cohort | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| All participants (n 8058) | Women (n 4269) | Men (n 3789) | All participants (n 72) | Women (n 31) | Men (n 41) | |||||||
| n | % | n | % | n | % | n | % | n | % | n | % | |
| Age (years) | ||||||||||||
| 65–74 | 4935 | 61.2 | 2542 | 59.5 | 2393 | 63.2 | 47 | 65.3 | 21 | 67.7 | 26 | 63.4 |
| ≥75 | 3123 | 38.8 | 1727 | 40.5 | 1396 | 36.8 | 25 | 34.7 | 10 | 32.3 | 15 | 36.6 |
| Local area | 3692 | 45.8 | 1963 | 46.0 | 1729 | 45.6 | 25 | 34.7 | 7 | 22.6 | 18 | 43.9 |
| BMI (kg/m2)† | ||||||||||||
| <18.5 | 623 | 7.7 | 443 | 10.4 | 180 | 4.8 | 7 | 9.7 | 3 | 9.7 | 4 | 9.8 |
| 18.5–24.9 | 5906 | 73.3 | 3061 | 71.7 | 2845 | 75.1 | 45 | 62.5 | 19 | 61.3 | 26 | 63.4 |
| ≥25 | 1529 | 19.0 | 765 | 17.9 | 764 | 20.1 | 20 | 27.8 | 9 | 29.0 | 11 | 26.8 |
| Current smoker | 857 | 10.6 | 152 | 3.6 | 705 | 18.6 | 6 | 8.3 | 1 | 3.2 | 5 | 12.2 |
| Alcohol drinker | 5252 | 65.2 | 2004 | 46.9 | 3248 | 85.7 | 56 | 77.8 | 17 | 54.8 | 39 | 95.1 |
| Living alone | 933 | 11.6 | 692 | 16.2 | 241 | 6.4 | 7 | 9.7 | 5 | 16.1 | 2 | 4.9 |
| HSES | 2767 | 34.3 | 1483 | 34.7 | 1284 | 33.9 | 25 | 34.7 | 10 | 32.3 | 15 | 36.6 |
| Education≥ 13 years | 1744 | 21.6 | 692 | 16.2 | 1052 | 27.8 | 22 | 30.6 | 7 | 22.6 | 15 | 36.6 |
| Denture use | 4941 | 61.3 | 2659 | 62.3 | 2282 | 60.2 | 39 | 54.2 | 17 | 54.8 | 22 | 53.7 |
| No medication | 1818 | 22.6 | 916 | 21.5 | 902 | 23.8 | 21 | 29.2 | 5 | 16.1 | 16 | 39.0 |
| Hypertension | 3031 | 37.6 | 1635 | 38.3 | 1396 | 36.8 | 22 | 30.6 | 9 | 29.0 | 13 | 31.7 |
| Diabetes | 809 | 10.0 | 315 | 7.4 | 494 | 13.0 | 9 | 12.5 | 3 | 9.7 | 6 | 14.6 |
| Hyperlipidemia | 767 | 9.5 | 506 | 11.9 | 261 | 6.9 | 13 | 13.1 | 7 | 22.6 | 6 | 14.6 |
HSES, high socio-economic status.
Missing values were supplemented using the multivariate imputation method: smoking status (n 366; 4.5 %), alcohol drinker (n 312; 3.9 %), family structure (n 626; 7.8 %), socio-economic status (n 389; 4.8 %), education attainment (n 939; 11.7 %), denture use (n 220; 2.7 %) and medications (n 648; 8.0 %).
BMI was calculated as body weight (kg) divided by height squared (m2).
Table 2 shows the comparison of TEE, measured using DLW, and uncalibrated and calibrated EI, assessed using FFQ data. Among all participants, the median TEE, uncalibrated EI and calibrated EI were 8559 kJ, 7088 kJ and 9269 kJ, respectively. The uncalibrated EI was significantly lower than the TEE (median difference = –1847 kJ; IQR: –2785 to –1096), but the calibrated EI (median difference = 463 kJ; IQR: –330 to 1541) was comparable to the TEE. Similar findings were observed when stratifying the sample by age, sex and BMI, with more marked results for men, individuals aged < 75 years, and for those with a BMI of ≥ 25 kg/m2. The uncalibrated (crude: r = 0.275; deattenuated: r = 0.306) and calibrated EI (crude: r = 0.517; deattenuated: r = 0.576) significantly correlated with the TEE measured using DLW. Moreover, Meng’s Z-test comparison revealed a significant difference in the correlation coefficient between uncalibrated and calibrated EI, estimated using FFQ data, against the TEE. The reproducibility (ICC) of the TEE measured using DLW was 0.619 (see online Supplemental Table 1), and it was higher for the calibrated EI (ICC = 0.982) than for the uncalibrated EI (ICC = 0.637; Table 3).
Table 2.
Validation of uncalibrated and calibrated energy intake against TEE measured using the DLW method
| TEE (kJ/d)† | Energy intake (kJ/d)† | Difference against DLW (kJ/d)‡ | CC by DLW§ | P-valueíí | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Uncalibrated | Calibrated | ||||||||||||||
| DLW | Uncalibrated | Calibrated | Uncalibrated | Calibrated | Crude | Deattenuated | Crude | Deattenuated | |||||||
| Median | IQR | Median | IQR | Median | IQR | Median | IQR | Median | IQR | r | r | r | r | ||
| Total (n 72) | 8559 | 7466–10 118 | 7088 | 6308–8003 | 9269 | 8249–10 060 | −1847 | −2785–-1096* | 463 | −330–1541 | 0.275* | 0.306* | 0.517* | 0.576* | 0.016 |
| Sex | |||||||||||||||
| Women (n 31) | 7742 | 6389–8859 | 6541 | 5977–7053 | 8173 | 7563–8504 | −1569 | −2168–-1064* | 722 | −695–1390 | 0.115 | 0.130* | 0.340* | 0.383* | 0.217 |
| Men (n 41) | 9489 | 8401–10 433 | 7837 | 6996–8420 | 9900 | 9469–10 267 | −2197 | −2954–-1453* | 285 | −218–1691 | 0.246 | 0.277* | 0.469* | 0.528* | 0.049 |
| Age (years) | |||||||||||||||
| <75 (n 47) | 8815 | 7046–10 185 | 6928 | 6015–7642 | 9132 | 8301–10 099 | −2168 | −2954–-1489* | 609 | −227–1384 | 0.284 | 0.310* | 0.598* | 0.652* | 0.014 |
| ≥75 (n 25) | 8401 | 7732–9619 | 7837 | 6726–8895 | 9360 | 7921–9797 | −1193 | −2140–-516 | 310 | −392–1723 | 0.168 | 0.191* | 0.333* | 0.377* | 0.290 |
| BMI (kg/m2) | |||||||||||||||
| <18.5 (n 7) | 6728 | 6370–8438 | 7533 | 6128–8913 | 9203 | 7521–9673 | −1353 | −1707–-289 | 1295 | 764–2929 | 0.464 | 0.526* | 0.821* | 0.931* | 0.076 |
| 18.5–24.9 (n 45) | 9288 | 7439–10 306 | 6996 | 6496–7897 | 8987 | 8189–10 099 | −1846 | −2863–-1097* | 77 | −1030–1067 | 0.213 | 0.237* | 0.475* | 0.529* | 0.016 |
| ≥25 (n 20) | 8093 | 7795–9109 | 7147 | 6077–7983 | 9462 | 8650–9978 | −2154 | −2770–-1528* | 942 | 108–1716 | 0.291 | 0.326* | 0.541* | 0.605* | 0.049 |
CC, correlation coefficient; DLW, doubly labelled water; IQR, interquartile range; TEE, total energy expenditure.
Indicates statistical significance (P < 0 05).
The variables are shown as median (IQR).
The values are shown as median difference (IQR). Statistical analysis was conducted by using a Wilcoxon signed-rank test.
The values are shown as Spearman’s rank correlation coefficient. Deattenuated correlation coefficients were calculated using Willett’s equation(3) to correct within-person variation in the twice-performed DLW method in May–June and August 2012. The deattenuated correlation was calculated according to the following: r c = r o (1 + (S2 w/S2 b)n)0.5; r c, corrected correlation coefficient; r o, observed correlation coefficient; S2 w, within-person variance; S2 b, between-person variance; n, number of replicates per person. Details of the within- and between-person variations used in this calculation are provided in Supplemental Table 1.
To compare the ranking of an individual’s energy intake between uncalibrated and calibrated estimates determined from FFQ data, we used the Meng et al. equation(27). If the results presented significant differences, these relationships were interpreted as not being equivalent.
Energy intake conversion factor: 1 kJ = 0.239 kcal.
Table 3.
Reproducibility of uncalibrated and calibrated energy intake estimated using FFQ data assessed twice
| Uncalibrated energy intake (kJ/d) | ICC§ | Calibrated energy intake (kJ/d) | ICC§ | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| First† | Second† | Difference‡ | First† | Second† | Difference‡ | |||||||||
| Median | IQR | Median | IQR | Median | IQR | Median | IQR | Median | IQR | Median | IQR | |||
| Total (n 72) | 7200 | 6300–8705 | 7088 | 6308–8003 | 0 | −383–1190 | 0.637* | 9182 | 8238–9954 | 9269 | 8249–10 060 | −35 | −81–24 | 0.982* |
| Sex | ||||||||||||||
| Women (n 31) | 6423 | 5994–6883 | 6541 | 5977–7053 | −1 | −861–485 | 0.492* | 8144 | 7758–8469 | 8173 | 7563–8504 | −18 | −78–68 | 0.921* |
| Men (n 41) | 8188 | 7347–9367 | 7837 | 6996–8420 | 157 | −85–1569 | 0.639* | 9852 | 9417–10 257 | 9900 | 9469–10 267 | −47 | −87–12 | 0.945* |
| Age (years) | ||||||||||||||
| <75 (n 47) | 6658 | 5894–8433 | 6928 | 6015–7642 | 0 | −465–1341 | 0.549* | 9077 | 8433–10 052 | 9132 | 8301–10 099 | −29 | −81–17 | 0.988* |
| ≥75 (n 25) | 7817 | 6883–9348 | 7837 | 6726–8895 | 316 | −19–1106 | 0.635* | 9195 | 7981–9815 | 9360 | 7921–9797 | −47 | −87–53 | 0.943* |
| BMI (kg/m2) | ||||||||||||||
| <18.5 (n 7) | 7704 | 5977–8707 | 7533 | 6128–8913 | −1 | −465–670 | 0.893* | 9169 | 7482–9742 | 9203 | 7521–9673 | −18 | −90–13 | 0.929* |
| 18.5–24.9 (n 45) | 7105 | 6407–8855 | 6996 | 6496–7897 | 0 | −330–1569 | 0.874* | 9057 | 8189–10 075 | 8987 | 8189–10 099 | −29 | −81–31 | 0.991* |
| ≥25 (n 20) | 7151 | 6001–8143 | 7147 | 6077–7983 | 0 | −170–487 | 0.874* | 9399 | 8643–9899 | 9462 | 8650–9978 | −52 | −81–7 | 0.991* |
ICC, intraclass correlation coefficient; IQR, interquartile range.
Statistical significance (P < 0.05).
First and second surveys were conducted on 14 February 2012 and August 2012, respectively. The variables are shown as median (IQR).
The values are shown as median difference (IQR). Statistical analysis was conducted using a Wilcoxon signed-rank test.
Intraclass correlation coefficients were analysed using Pearson’s correlation analysis.
Energy intake conversion factor: 1 kJ = 0.239 kcal.
Table 4 shows the sample size and number of survey repetitions required for uncalibrated and calibrated EI stratified by sex. To estimate a group’s ‘true’ mean uncalibrated and calibrated EI using FFQ data within a 95 % CI with 0.5 % deviation, 13 327 and 1972 participants were needed, respectively. For uncalibrated and calibrated EI, the FFQ needed to be repeated four times and once, respectively, to obtain a correlation coefficient (r) of 0.95 between an individual’s measured value and their ‘true’ unmeasured mean EI. These differences did not greatly differ when the sample was stratified by sex.
Table 4.
The sample size and frequency of surveys required for uncalibrated and calibrated energy intake estimation stratified by sex
| Uncalibrated EI | Calibrated EI | |||||
|---|---|---|---|---|---|---|
| Total (n 72) | Women (n 31) | Men (n 41) | Total (n 72) | Women (n 31) | Men (n 41) | |
| CVw (%)* | 12.6 | 9.1 | 15.2 | 0.9 | 1.0 | 0.7 |
| CVb (%)* | 26.6 | 16.2 | 28.4 | 11.3 | 6.6 | 5.6 |
| VR | 0.47 | 0.56 | 0.54 | 0.08 | 0.15 | 0.13 |
| Required group size† | ||||||
| Specified % deviation | ||||||
| 0.5 | 13 327 | 5320 | 15 938 | 1972 | 682 | 498 |
| 1.0 | 3332 | 1330 | 3985 | 493 | 170 | 125 |
| 2.5 | 533 | 213 | 638 | 79 | 27 | 20 |
| 5.0 | 133 | 53 | 159 | 20 | 7 | 5 |
| Required measurements‡ | ||||||
| Specified CC | ||||||
| 0.80 | 1 | 1 | 1 | 1 | 1 | 1 |
| 0.85 | 1 | 1 | 1 | 1 | 1 | 1 |
| 0.90 | 2 | 2 | 2 | 1 | 1 | 1 |
| 0.95 | 4 | 5 | 5 | 1 | 1 | 1 |
| Required measurements§ | ||||||
| Specified % deviation | ||||||
| 1.0 | 608 | 319 | 888 | 3 | 4 | 2 |
| 1.5 | 270 | 142 | 395 | 1 | 2 | 1 |
| 2.0 | 152 | 80 | 222 | 1 | 1 | 1 |
| 2.5 | 97 | 51 | 142 | 1 | 1 | 1 |
CC, correlation coefficient; CVb, coefficient of between-person variation; CVw, coefficient of within-person variation; EI, energy intake; VR, within-person/between-person variance ratio.
The within-person variance (CVw) and between-person variance (CVb) for EI were calculated using ANOVA.
The group size = 1.962×[(CVb2 + CVw2)/D02] was required to estimate a group’s ‘true’ mean EI within a 95 % CI with a specified % deviation (D0). All values represent group sizes.
The number of dietary survey repetitions (ND1) = [r2/(1 − r2)]×VR was required to obtain a specified CC between an individual’s estimated and unestimated ‘true’ mean EI, where r is the specified CC and an index of confidence related to an individual’s classification or ranking within a population. All values represent numbers of measurements.
The number of dietary survey repetitions (ND2) = (1.96 × CVw/D1)2 required to estimate an individual’s ‘true’ mean EI within a 95 % CI with a specified % deviation (D1). All values represent numbers of measurements.
We compared the calibrated and uncalibrated EI in the main cohort (Table 5). Among all participants, the median EI with and without calibration was 8756 kJ/d (IQR: 7973 to 9939) and 7222 kJ/d (IQR: 6219 to 8451), respectively (median difference = −1525 kJ (IQR:−2336 to−720); P < 0.01). Similar findings were observed when the sample was stratified by age, sex and BMI, with more marked results for BMI (<18.5 kg/m2: median difference = −829 kJ(IQR:−1547 to−179); 18.5–24.9 kg/m2: median difference = −1459 kJ (IQR:−2193 to−689);≥25 kg/m2: median difference = −2148 kJ (IQR:−3010 to −1309); P < 0.01). Although it was confirmed that the main cohort data were normally distributed, these results were similar to those of paired t test as a parametric statistic (see online Supplemental Table 2). These results were similar for EI/pBMR (see online Supplemental Table 3). Moreover, calibrated EI significantly correlated with age (r = −0.296), body weight (r = 0.707) and BMI (r = 0.367), but no correlation with these variables was evident for uncalibrated EI (see online Supplemental Table 4).
Table 5.
Comparison of calibrated and uncalibrated energy intakes in main cohort
| Energy intake (kJ/d)† | Difference‡ | |||||||
|---|---|---|---|---|---|---|---|---|
| Uncalibrated | Calibrated | Absolute (kJ/d) | Relative (%) | |||||
| Median | IQR | Median | IQR | Median | IQR | Median | IQR | |
| Total (n 8058) | 7222 | 6219–8451 | 8756 | 7973–9939 | −1525 | −2336–-720* | −17.4 | −26.2–-8.3* |
| Sex | ||||||||
| Women (n 4269) | 6554 | 5890–7324 | 8018 | 7576–8406 | −1420 | −2097–-718* | −17.7 | −26.0–-9.1* |
| Men (n 3789) | 8234 | 7236–9409 | 9987 | 9538–10 397 | −1692 | −2611–-727* | −17.0 | −26.3–-7.2* |
| Age (years) | ||||||||
| <75 (n 4935) | 7207 | 6210–8418 | 9048 | 8262–10 198 | −1824 | −2584–-1102* | −20.2 | −28.4–-11.9* |
| ≥75 (n 3123) | 7256 | 6233–8521 | 8160 | 7490–9460 | −1020 | −1773–-288* | −12.2 | −21.0–-3.3* |
| BMI (kg/m2) | ||||||||
| <18.5 (n 623) | 6877 | 6109–7913 | 7711 | 7160–8694 | −829 | −1547–-179* | −10.6 | −19.5–-2.4* |
| 18.5–24.9 (n 5906) | 7287 | 6277–8529 | 8674 | 7967–9914 | −1459 | −2193–-689* | −16.6 | −24.9–-7.9* |
| ≥25 (n 1529) | 7124 | 6079–8391 | 9371 | 8554–10 367 | −2148 | −3010–-1309* | −23.3 | −32.1–-14.2* |
IQR, interquartile range.
Indicates statistical significance (P < 0.05).
Values are expressed as median (IQR).
To compare the uncalibrated and calibrated energy intake, statistical analysis was conducted using a Wilcoxon signed-rank test.
Energy intake conversion factor: 1 kJ = 0.239 kcal.
Discussion
These results underscore the importance of biomarker calibration methods in nutritional epidemiological research. When compared to TEE measured using the DLW method, our results indicated that calibrated EI was more accurate and precise than uncalibrated EI. Additionally, we observed that the calibration approach substantially improved sample size and the number of survey repetitions required for EI stratified by sex, which was not considered in the previous study(5). Moreover, the uncalibrated EI derived from FFQ data was lower (about 17 %) than the calibrated EI in the main cohort. To the best of our knowledge, this is the first study to demonstrate that the calibration approach using a biomarker improves not only the systematic errors of self-reported EI but also sample size and the number of survey repetitions required for EI estimation. Therefore, these results may provide useful insights into the effective approach for improving statistical power to detect and verify diet–disease associations in cohort studies using an FFQ where sample size cannot be increased for a variety of reasons.
FFQ are widely used in large-scale epidemiological studies; however, their findings are more uncertain than those of carefully conducted DR or 24-h dietary recall(6,7). Our previous findings indicated that, compared with TEE measured using the DLW method, the 7-d DR underestimates EI by approximately 9 % whereas the FFQ underestimates EI by approximately 18 %(7). To rectify the underestimation of dietary intake estimated from FFQ, a recent review emphasised using the regression calibration approach to attenuate measurement errors of nutrient intake in nutritional epidemiology(31). According to a systematic review, to date, many studies have used this approach by estimating dietary intake using DR and 24-h dietary recall as references(31). However, it is unclear whether systematic errors due to self-report bias can be reduced using statistical techniques based on dietary intake data estimated using self-reported dietary assessment methods, such as DR and 24-h dietary recall(32). Our results indicate that the uncalibrated EI was significantly lower than the TEE, but the calibrated EI was comparable to the TEE, and similar findings were observed when stratifying the sample by age, sex and BMI. Objective biomarkers may not affect the systematic errors caused by reporting bias in self-reported dietary assessments, such as DR and 24-h dietary recall(1,6,7). Therefore, it is important to consider which biases can be rectified using the biomarker calibration approach, and our developed equation may attenuate some systematic errors related to variables such as age, sex and BMI.
Our findings indicate that calibrated EI had a higher reproducibility than uncalibrated EI. The lower within- and between-person variance observed for calibrated EI could be a possible explanation for this difference. When the within- and between-person variance in a population is high, surveys need to be conducted more frequently and with larger samples to accurately assess dietary intake(2). For the population in this study, assessment of uncalibrated and calibrated EI would require the FFQ to be repeated four times and once, respectively, to achieve a correlation coefficient of (r) < 0.95 between the observed and ‘true’ mean intake. Previous evidence indicates that the reproducibility (Pearson’s correlation coefficient) of TEE measured using DLW is 0.72(5). In fact, most biomarkers are considered representative of a person’s ‘true’ nutritional status, presuming that low within-person variation exists(33,34). Similarly, our results indicate that the reliability of the TEE estimates for replicate measures was rather good (ICC = 0.619), with the within-person variation for TEE being lower than that of the uncalibrated EI estimated using FFQ data (9.8 % for TEE; 12.6 % for EI). The above-mentioned studies and our findings indicate that calibrated EI is more reliable and reproducible compared to uncalibrated EI.
In this study, the uncalibrated EI was significantly lower than the calibrated EI in the main cohort (median difference: –1525 kJ) and lower than the TEE in the sub-cohort (median difference: –1847 kJ). These differences were similar to those between the calibrated EI and TEE. The fact that BMI increases concurrently with EI is predictable based on energy input and output(30). Some previous studies reported a larger magnitude of measurement errors and a higher frequency of EI underreporting in individuals with obesity(9–12). Similarly, our results revealed a larger difference between uncalibrated and calibrated EI in participants with a higher BMI. Moreover, the correlations between EI and age, body weight, and BMI were significant for the calibrated EI but not for the uncalibrated EI. The average BMI reportedly increases proportionally with a rise in a region’s population size(35) and the prevalence of obesity in adults is predicted to increase in the USA(35,36). Emphasising the importance of some behaviours can lead to an increase in systematic reporting bias because participants may modify their reports in the desired direction without actual behavioural change(37). As such, media and public health messages about the importance of combating obesity(38) that primarily focus on eating less could potentially explain why participants may underreport their EI. Similarly, age and sex are factors that contribute to misreporting of dietary intake(11,12). Using a biomarker calibration approach could reduce the age-, sex- and BMI-related systemic bias and may help verify diet–disease associations, especially in regions with a higher prevalence of obesity.
The main strength of this study is that it not only confirmed the accuracy of calibrated EI against TEE measured using DLW but also highlighted the reproducibility of calibrated EI assessed using FFQ data. These data are essential to confirm the precision of previously developed equations for calibration models. The reliability of the calibrated EI estimates was acceptable. However, the study also had a few methodological limitations. Firstly, the calibration equation used in this study was based on the TEE in a subsample of participants with stable body weight in the Kyoto–Kameoka Study(7). The TEE, measured using the DLW method, is assumed to provide a true reflection of EI in individuals with stable body weight. However, if the study cohort included participants with unstable body weight, the estimated calibrated EI could contain systematic errors. In addition, to evaluate the validity of DLW-calibrated EI, we used replicate measures of TEE measured using the DLW method in the population wherein the calibration equation was developed. Further evaluation is needed to verify this equation’s validity in other participants from the Kyoto–Kameoka Study. Secondly, since we relied on self-reported information for weight and height in this study, we were unable to completely exclude systematic errors due to self-reporting. For example, the BMI included in the DLW calibration equation was derived from self-reported data and could be inadequate as calibration factors. Nevertheless, calibration of the EI reduced the underestimation of EI against the TEE measured using the DLW technique. In addition, we previously reported that the estimates of self-reported height, body weight and BMI among older adults in this sub-cohort are sufficiently accurate and reproducible(16), similar to observations of another Japanese cohort study(39). Finally, this study used a new equation to calibrate EI calculated with a TEE measured using the DLW technique as a recovery biomarker. This equation may have excluded other covariates that were not assessed in the Kyoto–Kameoka Study but potentially contributed to the systematic measurement errors. This may be the cause of the lower value of the determinant coefficient (R2). These limitations may make generalisation of the results difficult. Therefore, verification by a well-designed study with a larger randomised sample is needed to elucidate whether the determinant coefficient of the calibration equation increases by further inclusion of covariates that may potentially contribute to the systematic measurement errors.
Recently, cohort studies reported that EI or protein intake estimated using the biomarker calibration approach is associated with the prevalence of frailty(15), incidence of diabetes(14), cancer(40) and risk of CVD events(41), whereas self-reported dietary intake demonstrated only weak(15) or no associations(14,40,41) with these factors. Perhaps, the difficulty in accurately measuring dietary intake from self-reported dietary assessments may explain why a clear association between diet and disease has not been established yet. Many authors consider that self-reported EI should not be taken into account when investigating the risk factors for diseases associated with overweight and obesity(14,15,40,41). Underreporting of EI by individuals with obesity may disturb the accurate estimation of the effect of EI on the risk of diseases, such as diabetes and heart disease, which are associated with overweight rather than underweight. We plan to apply these biomarker-calibrated EI in the diet–disease analyses of the Kyoto–Kameoka Study cohort. The use of this approach holds promise for providing accurate EI values that can help establish guidelines applicable to public health and clinical nutrition.
Conclusions
The findings of our study demonstrate that calibrated EI was more accurate and precise than uncalibrated EI against TEE measured using the DLW technique. Further, the uncalibrated EI values were approximately 17 % lower than calibrated EI values in the main cohort. Therefore, using biomarkers to calibrate EI could partially resolve the systematic errors that have hindered nutritional epidemiological research for several decades and may prove useful in closing the knowledge gap in diet–disease associations.
Acknowledgements
Acknowledgements: We thank all members of the Kyoto–Kameoka Study group for their valuable contributions. We acknowledge several administrative staff of Kameoka City and Kyoto Prefecture. We wish to express our gratitude to all the participants for their cooperation in this study. The authors also thank Shinkan Tokudome, who was a former director of the National Institute of Nutrition and Health for providing useful FFQ advice. We would like to thank Editage (www.editage.jp) for English-language editing. Financial support: The Kyoto–Kameoka Study was conducted with JSPS KAKENHI and was supported by a research grant provided to Misaka Kimura (grant number 24240091), Yosuke Yamada (grant number 15H05363) and Daiki Watanabe (grant number 21K17699); a grant and administrative support by the Kyoto Prefecture Community-based Integrated Elderly Care Systems Promotion Organization since 2011; and Kameoka City under the programme of the Long-term Care Insurance and Planning Division of the Health and Welfare Bureau for the Elderly, the Ministry of Health, Labour and Welfare, and the WHO Collaborating Centre on Community Safety Promotion. Conflicts of interest: There are no conflicts of interest. Authorship: The authors’ responsibilities were as follows: H.F., M.K. and Y.Y.: designed the research (project conception, development of overall research plan and study oversight); T.Y., E.Y., K.I.-T., N.E., M.K. and Y.Y.: conducted the research (data collection); D.W., H.N., C.G. and K.I.-T.: analysed the data or performed statistical analysis; D.W. and Y.Y.: data interpretation; D.W. and Y.Y.: literature review; D.W. and Y.Y. wrote the paper; D.W., T.Y., E.Y., H.N., C.G., K.I.-T., N.E., H.F., M.K. and Y.Y. had primary responsibility for the final content. All authors read and approved the final manuscript. Ethics of human subject participation: This study was conducted according to the guidelines laid down in the 1964 Declaration of Helsinki and all procedures involving research study participants were approved by the Research Ethics Committee of Kyoto Prefectural University of Medicine (RBMR-E-363), the National Institutes of Biomedical Innovation, Health and Nutrition (NIBIOHN-76-2), and Kyoto University of Advanced Science (No. 20-1). Informed consent was obtained from all individual participants.
Supplementary material
For supplementary material accompanying this paper visit https://doi.org/10.1017/S1368980021003785.
click here to view supplementary material
References
- 1. Korth AL, Bhutani S, Neuhouser ML et al. (2020) Comparison of methods used to correct self-reported protein intake for systematic variation in reported energy intake using quantitative biomarkers of dietary intake. J Nutr 150, 1330–1336. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Watanabe D, Nanri H, Yoshida T et al. (2019) Validation of energy and nutrition intake in Japanese elderly individuals estimated based on a short food frequency questionnaire compared against a 7-d dietary record: the Kyoto-Kameoka study. Nutrients 11, 688. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Willett W (2012) Nutritional Epidemiology, 3rd ed. New York: Oxford University Press. [Google Scholar]
- 4. Livingstone MB & Black AE (2003) Markers of the validity of reported energy intake. J Nutr 133, Suppl. 3, 895S–920S. [DOI] [PubMed] [Google Scholar]
- 5. Neuhouser ML, Tinker L, Shaw PA et al. (2008) Use of recovery biomarkers to calibrate nutrient consumption self-reports in the women’s health initiative. Am J Epidemiol 167, 1247–1259. [DOI] [PubMed] [Google Scholar]
- 6. Park Y, Dodd KW, Kipnis V et al. (2018) Comparison of self-reported dietary intakes from the automated self-administered 24-h recall, 4-d food records, and food-frequency questionnaires against recovery biomarkers. Am J Clin Nutr 107, 80–93. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Watanabe D, Nanri H, Sagayama H et al. (2019) Estimation of energy intake by a food frequency questionnaire: calibration and validation with the doubly labeled water method in Japanese older people. Nutrients 11, 1546. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Prentice RL, Mossavar-Rahmani Y, Huang Y et al. (2011) Evaluation and comparison of food records, recalls, and frequencies for energy and protein assessment by using recovery biomarkers. Am J Epidemiol 174, 591–603. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Schoeller DA, Thomas D, Archer E et al. (2013) Self-report-based estimates of energy intake offer an inadequate basis for scientific conclusions. Am J Clin Nutr 97, 1413–1415. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Tomoyasu NJ, Toth MJ & Poehlman ET (1999) Misreporting of total energy intake in older men and women. J Am Geriatr Soc 47, 710–715. [DOI] [PubMed] [Google Scholar]
- 11. Murakami K & Livingstone MB (2015) Prevalence and characteristics of misreporting of energy intake in US adults: NHANES 2003–2012. Br J Nutr 114, 1294–1303. [DOI] [PubMed] [Google Scholar]
- 12. Murakami K, Livingstone MBE, Okubo H et al. (2018) Prevalence and characteristics of misreporting of energy intake in Japanese adults: the 2012 national health and nutrition survey. Asia Pac J Clin Nutr 27, 441–450. [DOI] [PubMed] [Google Scholar]
- 13. Lachat C, Hawwash D, Ocke MC et al. (2016) Strengthening the reporting of observational studies in epidemiology-nutritional epidemiology (STROBE-nut): an extension of the STROBE statement. PLoS Med 13, e1002036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Tinker LF, Sarto GE, Howard BV et al. (2011) Biomarker-calibrated dietary energy and protein intake associations with diabetes risk among postmenopausal women from the women’s health initiative. Am J Clin Nutr 94, 1600–1606. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. Watanabe D, Yoshida T, Nanri H et al. (2021) Association between the prevalence of frailty and doubly labeled water-calibrated energy intake among community-dwelling older adults. J Gerontol A Biol Sci Med Sci 76, 876–884. [DOI] [PubMed] [Google Scholar]
- 16. Watanabe D, Yoshida T, Watanabe Y et al. (2020) A U-shaped relationship between the prevalence of frailty and body mass index in community-dwelling Japanese older adults: the Kyoto-Kameoka study. J Clin Med 9, 1367. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Yamada Y, Nanri H, Watanabe Y et al. (2017) Prevalence of frailty assessed by fried and Kihon checklist indexes in a prospective cohort study: design and demographics of the Kyoto-Kameoka longitudinal study. J Am Med Dir Assoc 18, 733.e7–733.e15. [DOI] [PubMed] [Google Scholar]
- 18. Imaeda N, Goto C, Tokudome Y et al. (2007) Reproducibility of a short food frequency questionnaire for Japanese general population. J Epidemiol 17, 100–107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Tokudome S, Goto C, Imaeda N et al. (2004) Development of a data-based short food frequency questionnaire for assessing nutrient intake by middle-aged Japanese. Asian Pac J Cancer Prev 5, 40–43. [PubMed] [Google Scholar]
- 20. Tokudome Y, Goto C, Imaeda N et al. (2005) Relative validity of a short food frequency questionnaire for assessing nutrient intake v. 3-d weighed diet records in middle-aged Japanese. J Epidemiol 15, 135–145. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Council for Science and Technology & Ministry of Education, Culture, Sports, Science and Technology (2001) Standard Tables of Food Composition in Japan, Fifth Revised and Enlarged Edition. Tokyo, Japan: National Printing Bureau. [Google Scholar]
- 22. Yamada Y, Hashii-Arishima Y, Yokoyama K et al. (2018) Validity of a triaxial accelerometer and simplified physical activity record in older adults aged 64–96 years: a doubly labeled water study. Eur J Appl Physiol 118, 2133–2146. [DOI] [PubMed] [Google Scholar]
- 23. Weir JB (1949) New methods for calculating metabolic rate with special reference to protein metabolism. J Physiol 109, 1–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. Sagayama H, Yamada Y, Racine NM et al. (2016) Dilution space ratio of 2H and 18O of doubly labeled water method in humans. J Appl Physiol 120, 1349–1354. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25. Black AE, Prentice AM & Coward WA (1986) Use of food quotients to predict respiratory quotients for the doubly-labelled water method of measuring energy expenditure. Hum Nutr Clin Nutr 40, 381–391. [PubMed] [Google Scholar]
- 26. van Buuren S & Groothuis-Oudshoorn K (2011) Mice: multivariate imputation by chained equations in R. J Stat Softw 45, 1–67. [Google Scholar]
- 27. Meng X, Rosenthal R & Rubin DB (1992) Comparing correlated correlation coefficients. Psychol Bull 111, 172–175. [Google Scholar]
- 28. Ganpule AA, Tanaka S, Ishikawa-Takata K et al. (2007) Interindividual variability in sleeping metabolic rate in Japanese subjects. Eur J Clin Nutr 61, 1256–1261. [DOI] [PubMed] [Google Scholar]
- 29. Miyake R, Tanaka S, Ohkawara K et al. (2011) Validity of predictive equations for basal metabolic rate in Japanese adults. J Nutr Sci Vitaminol 57, 224–232. [DOI] [PubMed] [Google Scholar]
- 30. Hall KD, Sacks G, Chandramohan D et al. (2011) Quantification of the effect of energy imbalance on bodyweight. Lancet 378, 826–837. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31. Bennett DA, Landry D, Little J et al. (2017) Systematic review of statistical approaches to quantify, or correct for, measurement error in a continuous exposure in nutritional epidemiology. BMC Med Res Methodol 17, 146. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32. Looman M, Boshuizen HC, Feskens EJ et al. (2019) Using enhanced regression calibration to combine dietary intake estimates from 24 h recall and FFQ reduces bias in diet-disease associations. Public Health Nutr 22, 2738–2746. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Kaaks RJ (1997) Biochemical markers as additional measurements in studies of the accuracy of dietary questionnaire measurements: conceptual issues. Am J Clin Nutr 65, 1232S–1239S. [DOI] [PubMed] [Google Scholar]
- 34. Neuhouser ML, Patterson RE, King IB et al. (2003) Selected nutritional biomarkers predict diet quality. Public Health Nutr 6, 703–709. [DOI] [PubMed] [Google Scholar]
- 35. NCD Risk Factor Collaboration (2019) Rising rural body-mass index is the main driver of the global obesity epidemic in adults. Nature 569, 260–264. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36. Ward ZJ, Bleich SN, Cradock AL et al. (2019) Projected U.S. state-level prevalence of adult obesity and severe obesity. N Engl J Med 381, 2440–2450. [DOI] [PubMed] [Google Scholar]
- 37. Taber DR, Stevens J, Murray DM et al. (2009) The effect of a physical activity intervention on bias in self-reported activity. Ann Epidemiol 19, 316–322. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38. Hilton S, Patterson C & Teyhan A (2012) Escalating coverage of obesity in UK newspapers: the evolution and framing of the “obesity epidemic” from 1996 to 2010. Obesity 20, 1688–1695. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39. Wada K, Tamakoshi K, Tsunekawa T et al. (2005) Validity of self-reported height and weight in a Japanese workplace population. Int J Obes 29, 1093–1099. [DOI] [PubMed] [Google Scholar]
- 40. Prentice RL, Shaw PA, Bingham SA et al. (2009) Biomarker-calibrated energy and protein consumption and increased cancer risk among postmenopausal women. Am J Epidemiol 169, 977–989. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41. Prentice RL, Huang Y, Kuller LH et al. (2011) Biomarker-calibrated energy and protein consumption and cardiovascular disease risk among postmenopausal women. Epidemiology 22, 170–179. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
For supplementary material accompanying this paper visit https://doi.org/10.1017/S1368980021003785.
click here to view supplementary material


