Supporting Information

Files in this Data Supplement:

Supporting Appendix

The stress-free boundary conditions at are

, ,

Assuming perfect bonding at the rigid spherical inclusion-tissue interface, one requires

The condition that the normal stress in the plate in the x direction tend to a uniform stress T₀ as x tends to is given by

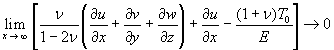. [4]

A general solution of the Eqs. 1-4 is represented as a combination of six harmonic functions. Components of the displacement vector u() are expressed in terms of these functions as follows:

 [5]

where

 [6]

,

and and G denote Poisson's ratio and the shear modulus respectively. The displacement and stress fields derived from these harmonic stress functions satisfy the governing Eq. 1 in the absence of body forces.

First, we choose harmonic functions and in the following form:

 [7]

,

where; and are Legendre functions of the first kind of order n and associated Legendre function of the first kind of order n and degree m, respectively. Substituting expressions 7 for harmonic functions and into expressions 5 one can calculate the corresponding displacement and stress fields:

 [8]

, [9]

where E is Young's modulus.

Expressions 8 and 9 represent a solution of the problem of a thick plate under uniaxial tension parallel to the x axis in the absence of an inclusion.

Eq. 9 shows that this solution gives no traction at the surfaces of the plate . The components of the displacement on the inclusion surface are

 [10]

To satisfy zero displacement boundary conditions at the inclusion interface (3) when an inclusion is present, we construct auxiliary stress functions using suitable harmonic functions such that they would yield no traction on the plate surfaces

 [11]

and satisfy the following boundary conditions at :

 [12]

Expressions 11 and 12 are split into an axisymmetric part that does not depend on j and an asymmetric part that is a function of j.

First, we construct the auxiliary stress functions for the case of a stress distribution that is axisymmetric about the z axis as follows:

, [13]

where are unknown coefficients of the spherical stress functions, are Legendre functions, and

, [14]

,

where is a Bessel function of the first kind of the zero order and are arbitrary cylindrical functions of.

The integral relation

 [15]

allows one to express the spherical stress functions (13) in cylindrical coordinates and rewrite the stress-free boundary conditions at (11) as follows:

[16]

The next step is to express cylindrical functions in terms of the spherical functions (13) by applying Hankel transforms to the stress free boundary conditions (16) and solving the four linear algebraic equations simultaneously for:

, [17]

where

To satisfy remaining boundary conditions at the inclusion interface (12), one has to express the cylindrical functions (14) in spherical coordinates using following relations:

 [18]

The resulting expansions of the cylindrical functions and (14) are given by

, , [19]

where coefficients and are determined by

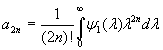, , [20]

,.

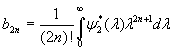Substituting given by Eq. 17 into Eqs. 20, expressions for and can be obtained in terms of the unknown spherical coefficients. These expressions contain integrals with respect to that have to be evaluated numerically.

Finally, using stress functions (5) and satisfying boundary conditions (10), one can obtain the resulting system for the axisymmetric case

 [21]

 [22]

Equating coefficients of each Legendre function in Eq. 21 or its derivative in Eq. 22 to zero, one obtains a system of linear equations for the unknown coefficients of the spherical harmonics. The axisymmetric solution of the problem (1-4) is determined by truncating and solving this system. After solving for the coefficients, one can calculate the stresses and deformations at any point within the plate.

For the asymmetric problem, the pure shear spherical and cylindrical harmonics are defined by

, ,

, [23]

,,

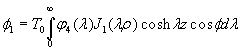
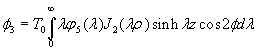
 [24]

,,

,

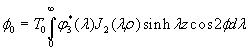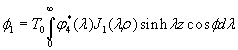
where and are unknown coefficients of the spherical harmonics; and are arbitrary functions.

In a similar procedure to that described in the previous section, one satisfies boundary conditions 11 and 12 by using relations 15 and 18. The final equations for the asymmetric case are

 [25]

Equating coefficients of each Legendre function in Eq. 25 to zero, one obtains a system of linear equations. The asymmetric solution of Eqs. 1-4 is determined by solving the linear simultaneous equations for the parametric coefficients of the spherical harmonics. Solving for the coefficients, one can calculate the stresses and deformations corresponding to the asymmetric case at any point within the plate.

Final expressions for the displacement and stress fields are given by

u = u₁ + u₂,

s_i = s_i1 + s_i2,

where u₁, s_i1 and u₂, s_i2 represent the axisymmetric and the symmetric parts, respectively.

Supporting Methods

Initial reconstructions of the whole volumes were carried out at 35-mm voxel resolution. Because of computational limitations to handle digital data sets higher than 800 MB, the digital volumes were sectioned in consecutive volumes of interest consisting of the whole vessel circumference and »3 mm in height, which were reconstructed at 7-mm resolution, resulting in eight to nine sections per sample. Density-calibrated images were segmented by using the global threshold method built-in MicroView visualization and analysis software (GE Healthcare; Version 2.1.2). The presence of mineral, soft tissue, lipid, and air in the vessels was distinguished by the high sensitivity of the system to the different densities on each of these compartments. Mineralized tissue particles were investigated on each volumes of interest, and isosurfaces of microcalcifications in the fibrous caps of atherosclerotic lesions were rendered by using the MicroView software.