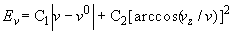 ,
,Fig. 9.
Monte Carlo simulations of DNA braids. A discrete worm-like chain model was used to simulate equilibrium sets of the braid conformations. The excluded volume and electrostatic interactions between segments of the DNA chain are taken into account in the model via the concept of effective diameter, d (3, 4). Force, F/2, was applied to the right end of each chain and directed along the x-axis as shown. This added an extra term to the braid energy:Eext = - F(x1 + x2)/2,
where x1 and x2 correspond to the right ends of the two chains. The left end of the braid was held immobile during the Metropolis simulation procedure. The right end of the braid was free to change its position during the simulation to allow variation of the extension of the braid. Although the vector, which connected the right ends changed its value during the simulations, we introduced an extra potential into the Monte Carlo procedure to restrict these changes:
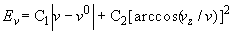 ,
,
where C1 and C2 are constants equal to 10 kT, v and vz are the absolute value and z-component of v, and v0 is the absolute value of v at the beginning of a simulation run. The first term of the potential restricts the length variation of v, and the second term aligns it along the z-axis. To specify the topology of the braid we closed each model chain by long segments, parallel to the direction of the force, and by a large loop. The topology of the braids was controlled by calculating the Alexander polynomial for the two chains, Δ(s, t) for s = - 1, t = - 1 (5). For the torus links formed by the braids, Δ(- 1, - 1) equals the linking number of the two closed chains, lk. Visual inspection of the numerous braid conformations showed that keeping the condition Δ(- 1, - 1) = lk was sufficient to maintain the braid topology during the simulation runs. Equilibrium sets of chain conformations for different values of the force and lk were constructed by using the Metropolis procedure (6). The two types of chain displacements used in the simulations were described earlier (7). To obtain representative equilibrium conformations, up to 2 ´ 108 elementary displacements were produced for each value of F and lk. The DNA persistence length was set equal to 50 nm (8). The effective diameter was equal to 5 nm; this corresponds to a monovalent salt concentration of 0.2 M (3).
3. Stigter, D. (1977) Biopolymers 16, 1435-1448.
4. Vologodskii, A. & Cozzarelli, N. (1995) Biopolymers 35, 289-296.
5. Vologodskii, A. V., Lukashin, A. V. & Frank-Kamentskii, M. D. (1975) Sov. Phys. JETP 40, 932-936.
6. Metropolis, N., Rosenbluth, A. W., Rosenbluth, M. N., Teller, A. H. & Teller, E. (1953) J. Chem. Phys. 21, 1087-1092.
7. Vologodskii, A. V. & Cozzarelli, N. R. (1994) Annu. Rev. Biophys. Biomol. Struct. 23, 609-643.
8. Hagerman, P. J. (1988) Annu. Rev. Biophys. Biophys. Chem. 17, 265-286.