Supporting Information

Files in this Data Supplement:

Fig. 4. Long-term bicuculline and saclofen (BIC+SAC) treatment does not affect antagonist efficacy in blocking spontaneous and evoked GABAergic inhibitory postsynaptic currents (IPSCs). We were concerned that GABA signaling in the SCN could be up-regulated in response to long-term GABA blockade. To test for this, we performed whole-cell recordings of dispersed SCN neurons cultured in the presence or absence of BIC+SAC for 10 days. (A) Representative current traces of a neuron treated with BIC+SAC for 10 days before recording under four conditions: control (spontaneous IPSCs after washout of BIC+SAC), BIC+SAC, high K⁺ (10 mM KCl-evoked IPSCs after washout of BIC+SAC), and high K⁺ with BIC+SAC. BIC+SAC blocked GABA-induced IPSCs in the presence or absence of high K⁺ by >99.6% regardless of prior treatment (n = 9 neurons in three cultures per group). (B) Average IPSC frequency under four recording conditions for previously untreated neurons (open bars) and neurons treated continuously for 10 days with BIC+SAC (filled bars). There was no difference in IPSC frequency between neurons cultured for the previous 10 days without BIC+SAC and those cultured with BIC+SAC [not significant (N.S.); P > 0.2 for all four conditions, ANOVA]. We conclude that continuous BIC+SAC effectively blocked GABA-evoked IPSCs for at least 10 days with no homeostatic increase in GABA signaling or sensitivity to GABA. The following methods were used for whole-cell recording. C57BL/6 SCN neurons were cultured in high-density dispersals for 2-3 weeks before whole-cell voltage-clamp recording. For the final 10 days before recording, some neuronal cultures were treated continuously with BIC+SAC. During recording, cultures were perfused at 1-2 ml/min with Tyrode's solution containing 150 mM NaCl, 4 mM KCl, 2 mM CaCl₂, 2 mM MgCl₂, 10 mM glucose, and 10 mM Hepes (pH adjusted to 7.4 with NaOH). Whole-cell electrodes were filled with 140 mM cesium glucuronate, 5 mM CsCl, 5 mM MgCl₂, 10 mM EGTA, 5 mM ATP, 1 mM GTP, and 10 mM Hepes (pH adjusted to 7.4 with CsOH). The reference electrode was in a well filled with internal solution that connected to the bath by an agar bridge equilibrated with 4 M KCl. Spontaneous IPSCs were recorded at 0 mV with an Axopatch 200A amplifier (Molecular Devices, Sunnyvale, CA), filtered at 1 kHz, and digitized at 10 kHz. In some experiments, spontaneous IPSC frequency was elevated by local perfusion with 10 mM KCl. IPSC frequency was quantified using in-house software.

Fig. 5. Comparison of simulations of and recordings from SCN slices during drug treatment. Cycle-to-cycle Per1::luc rhythm amplitudes for control and BIC+SAC-treated SCN slices are best fit by a model in which neurons show a narrow distribution of periods and minimal desynchrony and rhythms that do not damp over time (model A), whereas tetrodotoxin (TTX) and pertussis toxin (PTX) data are best fit by model C (damping plus desynchrony). Peak-to-trough amplitudes (mean ± SEM) are plotted as in Fig. 1B. Untreated (open circles) and BIC+SAC-treated slices (filled circles) showed minimal damping of rhythms relative to TTX- (open triangles) and PTX-treated slices (filled triangles). Lines show best-fit results generated by model A (red lines), model B (damping with minimal desynchrony; green lines), and model C (blue lines). Parameter values for each best-fit line are shown in Table S1. We used a six-parameter simulation of a population of oscillators to fit our experimental Per1::luc data: (i) the number of oscillators, N_Osc; (ii) their mean oscillatory period, t_Osc; (iii) the SD of their mean oscillatory period, st,; (iv) the fraction of damped oscillators, f_Damp; (v) the decay lifetime for the amplitude of the oscillators that damp, t_Damp; and (vi) the initial amplitude of all oscillators, Amp. The simulation used nonlinear least-squares optimization of the parameter values (1) to calculate total bioluminescence, y(t), from the ensemble of oscillators:

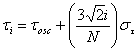
where ; ; and .

Modeled by this formulation, y(t) cycled with its first peak at time t_Ref and subsequent peaks at integer multiples of t_Osc. The distribution of oscillators had a Gaussian distribution of periods that spanned approximately ±4.25 SD values from the mean period. After time t_Ref, phase desynchrony was allowed to occur because of the range of intrinsic periods. Damping of oscillatory amplitude in a fraction of the oscillators, f_damp, initiated after time t_Ref, was modeled simply as an exponential decay with a damping lifetime, t_Damp according to:

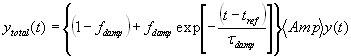
Constraints were imposed during parameter optimization such that Amp ³ 0.0, st ³ 0.0, t_Damp ³ 0.0 and 0.0 £ f_Damp £ 1.0. For all three models (Fig. 1), we used 10,000 oscillators with a mean period of 24.35 h. After the simulation generated a set of best-fit parameters, it calculated their confidence limits according to published methods (2).

Fig. 6. PTX specifically damps circadian rhythms in the SCN and not in the liver. Bioluminescence rhythms from untreated PER2::LUC mouse liver (open squares) damped at the same rate as PTX-treated liver (filled squares) and PTX-treated SCN from either Per1::luc rats (filled circles; same data as Fig. 1B) or PER2::LUC mice (filled triangles; P > 0.05 for all cycles measured, ANOVA with post hoc Scheffé test). Symbols show peak-to-trough amplitudes (mean ± SEM; n = at least four explants per point) during drug treatment normalized to the amplitude of the last cycle before the addition of drugs or control medium.

Fig. 7. PTX, but not BIC+SAC, blocks restoration of function to vasoactive intestinal peptide-null (VIP-^/-) neurons by VIP receptor (VPAC₂) agonist treatment. (A) Firing-rate traces for two arrhythmic VIP-^/- SCN neurons treated with Ro 25-1553 (arrowheads) every 24 h for 6 days in the continuous presence of either BIC+SAC (Left) or PTX (Right). Note that daily rhythms were induced by the VPAC₂ agonist in the presence of BIC+SAC but not in PTX. (B) Firing-rate traces for two rhythmic VIP-^/- SCN neurons from the same cultures shown in A. (C) Distribution of circadian phases for rhythmic VIP-^/- neurons within representative cultures were random before treatment (n = 20 neurons, r = 0.14, P > 0.6 for BIC+SAC-treated neurons; and n = 31 neurons, r = 0.06, P > 0.9 for PTX-treated neurons, Rayleigh tests) and during daily Ro 25-1553 + PTX treatment (n = 20, r = 0.25, P > 0.25), but they became significantly clustered during daily Ro 25-1553 + BIC+SAC treatment (n = 41, r = 0.50, P < 0.01). Note that neuronal firing tended to peak (average acrophase shown by the arrow) just before the final Ro 25-1553 application (arrowhead). (D) Period distributions for all rhythmic VIP-^/- neurons before and during treatments. The distribution of periods became significantly narrower during Ro 25-1553 + BIC+SAC treatment (P < 0.05, Levene and Brown-Forsythe tests). The period distribution did not change during daily Ro 25-1553 + PTX treatment (P > 0.05). (Insets) Proportion of rhythmic (black) VIP-^/- neurons from all recordings, which increased to wild-type levels during daily Ro 25-1553 + BIC+SAC treatment but did not change during Ro 25-1553 + PTX treatment.

Fig. 8. Model for maintenance of rhythms and synchrony in SCN neurons by circadian regulation of G protein signaling. During the subjective day, VIP release activates VPAC₂ receptors (red), which activate adenylyl cyclase (AC; blue) through G_s, increasing intracellular cAMP levels. Subsequent activation of protein kinase A (PKA) and phosphorylation of cAMP response element-binding protein (CREB; green) induces Period1 and Period2 transcription by means of CREB response elements (CREs) on their respective promoters. During the subjective night, VIP release and Ga_s-mediated signaling diminish. G_i/o becomes activated by Dexras1 (yellow) or by neurotransmitter-mediated activation of an unknown G_i/o-coupled receptor (violet). G_i/o inhibits AC, down-regulating the cAMP cascade and, ultimately, decreases Period transcription. In this model, the daily rhythm in the ratio of G_s to G_i/o activity synchronizes pacemaking neurons by shifting Period expression, and it sustains rhythms in nonpacemaking neurons by augmenting Period expression. Thus, inhibition of VPAC₂-mediated G_s signaling or blocking G_i/o signaling with PTX disrupts rhythms in SCN neurons and prevents their synchronization. In support of this model, VIP release is circadian in the SCN in vitro (3), and light can cause its release in vivo (4). SCN cAMP content shows VIP-dependent circadian rhythmicity (5, 6), and CREB-mediated gene expression is also rhythmic in the SCN (7). Inhibition of AC likely leads to a decrease in cAMP (8) and CRE-mediated transcription of Period genes (9, 10). We found that cholera toxin, which constitutively activates G_s, leading to constant cAMP production, causes damping of ensemble rhythms similar to PTX or loss of VIP signaling. Changes in cAMP or PKA have been shown to phase-shift the SCN (11). VIP phase-shifts SCN-firing rhythms by a PKA-dependent intracellular mechanism (12). Interestingly, Per1::luc expression is low (even in rhythmic cells) in the SCN of mice lacking VPAC₂ (13). Finally, CRE-mediated induction of Period transcription correlates with entrainment (9, 14-19). Thus, we predict that both G_s and G_i/o activities are required for daily rhythms in cAMP, CREB activity, and Period gene expression in the majority of SCN neurons and for synchronization of these rhythms between neurons.

1. Johnson ML, Frasier SG (1985) Methods Enzymol 117:301-342.

2. Straume M, Frasier-Cadoret SG, Johnson ML (1991) Topics in Fluorescence Spectroscopy, ed Lakowicz JR (Plenum, New York), pp 177-240.

3. Shinohara K, Funabashi T, Mitushima D, Kimura F (2000) Neurosci Res 38:43-47.

4. Shinohara K, Tominaga K, Inouye ST (1999) Neurosci Res 33:105-110.

5. Yamazaki S, Maruyama M, Cagampang FR, Inouye ST (1994) Brain Res 651:329-331.

6. Gerhold LM, Rosewell KL, Wise, PM (2005) J Neurosci 25:62-67.

7. Obrietan K, Impey S, Smith D, Athos J, Storm DR (1999) J Biol Chem 274:17748-17756.

8. Fitzgerald LR, Mannan IJ, Dytko GM, Wu HL, Nambi P (1999) Anal Biochem 275:54-61.

9. Gau D, Lemberger T, von Gall C, Kretz O, Le Minh N, Gass P, Schmid W, Schibler U, Korf HW, Schutz G (2002) Neuron 34:245-253.

10. Travnickova-Bendova Z, Cermakian N, Reppert SM, Sassone-Corsi P (2002) Proc Natl Acad Sci USA 99:7728-7733.

11. Tischkau SA, Gallman EA, Buchanan GF, Gillette MU (2000) J Neurosci 20:7830-7837.

12. Meyer-Spasche A, Piggins HD (2004) Neurosci Lett 358:91-94.

13. Maywood ES, Reddy AB, Wong GK, O'Neill JS, O'Brien JA, McMahon DG, Harmar AJ, Okamura H, Hastings MH (2006) Curr Biol 16:599-605.

14. Tischkau SA, Weber ET, Abbott SM, Mitchell JW, Gillette MU (2003) J Neurosci 23:7543-7550.

15. Shigeyoshi Y, Taguchi K, Yamamoto S, Takekida S, Yan L, Tei H, Moriya T, Shibata S, Loros JJ, Dunlap JC, et al. (1997) Cell 91:1043-1053.

16. Takumi T, Matsubara C, Shigeyoshi Y, Taguchi K, Yagita K, Maebayashi Y, Sakakida Y, Okumura K, Takashima N, Okamura H (1998) Genes Cells 3:167-176.

17. Albrecht U, Sun ZS, Eichele G, Lee CC (1997) Cell 91:1055-1064.

18. Shearman LP, Zylka MJ, Weaver DR, Kolakowski LF, Reppert SM (1997) Neuron 19:1261-1269.

19. Numano R, Yamazaki S, Umeda N, Samura T, Sujino M, Takahashi R, Ueda M, Mori A, Yamada K, Sakaki Y, et al. (2006) Proc Natl Acad Sci USA 103:3716-3721.

Table 1. Best-fit parameters for three models to experimental Per1::luc ensemble rhythm amplitude

The three models were run to determine whether desynchrony among a population of sustained oscillators (model A), damping of individual oscillators (model B), or simultaneous desynchrony and damping (model C) could explain Per1::luc patterns recorded from SCN cultured with or without BIC+SAC, PTX, or TTX. σ_τ, is standard deviation of period distribution (in hours), fDmp is the percentage of damped oscillators in the population, and VOF is the variance of fit. Values that are bracketed were held constant during the data-fitting process. Results from the model that best fit the experimental data (i.e., smallest VOF) are in bold.