Chabertand Viovy. 10.1073/pnas.0708321105. |
Fig. 5. Trajectories of droplets with various radii in the focusing channel, as predicted by the model in ref. 16 for a cylindrical geometry. The displacement is calculated in a plane encompassing the channel's axis using Eq. S3 (SI Text), assuming a 3D circular parabolic flow, the droplet's center of mass starting in the plane 4.5 mm from the channel's axis.

Fig. 6. This sequence exemplifies the encapsulation and sorting of a cancerous T lymphocyte (fluorescent, appearing in white, marked with an arrow) out of a concentrated RBC suspension. Although many RBC are present around the lymphocyte, it gets encapsulated in a drop without any RBC and sorted.
Movie 1. Movie 1 exemplifies the cell encapsulation process (40x objective). The sequence lasts »18 ms in real time and is slowed down 760 times.
Movie 2. Movie 2 is a close up (40x objective) of positive drops sorting after encapsulation. The sequence lasts »28 ms in real time and is slowed down 780 times.
Movie 3. Movie 3 is a real time sequence (7.4 s, 20x objective) of single cells encapsulation and sorting (Qo = 150 ml/h, Qc = 7 ml/h).
Movie 4. Movie 4 displays the encapsulation and collection of single cells at QO = 150 ml/h, QC = 7 ml/h, (observed using a 20x objective). The sequence lasts »107 ms real time, and is slowed down 140 times.
SI Text
Details for theoretical estimation of the lateral distance traveled by droplets of different sizes.
The Poiseuille flow profile in the coordinate system of Fig. 1A (infinite slit) is described by:
![]()
where VM is the maximum speed (at y = WF/2) and WF is the width of the channel (see Fig. 1A).
According to Chan and Leal (1), the instantaneous drop migration velocity along y axis is given by:
 [S1]
[S1]
where ho is the oil viscosity, g is the interfacial tension between oil and aqueous solution, a is the drop radius, and a~0.66 is a dimensionless coefficient depending on the dispersed and continuous phase viscosity ratio (a can be positive or negative depending on this viscosity ratio).
The drop flows along the x axis in the Poiseuille profile at a speed U:
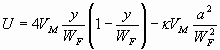 [S2]
[S2]
where the dimensionless coefficient k~0.004 depends again on the dispersed and continuous phase viscosity ratio.
The droplets trajectory is calculated using:

which using S1 and S2 easily integrates to Eq. 1:
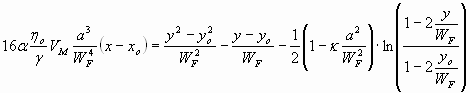 [1]
[1]
To check for the robustness of our "infinite slit" approximation, we also modeled the focusing channel by a cylindrical pipe with a 20 mm radius. Chan and Leal (1) get for the droplets trajectories:
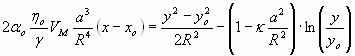 [S3]
[S3]
where ao~1.10 is again a dimensionless coefficient depending on the dispersed and continuous phase viscosity ratio, x and xo are the droplet coordinates along the cylindrical channel axis, and y and yo denote the distances of the droplet to the channel axis.
Numerical results of Eq. S3 for lateral distances traveled in a plane bisecting the cylindrical channel axis by droplets starting at yo = 15.5 mm from the channel wall and for (x-xo) = 500 mm are summarized on a plot of droplet trajectories in SI Fig. 5, for various drop radii and an oil flow rate Qo = 100 ml/h (g = 5 mN/m; ho = 120 mPa.s). As can be seen, the trajectories calculated using a cylindrical pipe approximation show a behavior qualitatively similar to the curves calculated using an infinite slit approximation (Fig. 4).
More generally, it should be noted here that the drop migration effect is physically distinct from the effect used in ref. 2 and known as pinched flow fractionation (PFF). PFF uses asymmetric focusing of rigid particles to sort them by size, but this size-sorting effect is due to the steric interaction of the particles with the walls, and not to a shear-induced migration effect. Shear-induced migration of rigid particles in a Newtonian fluid is indeed only due to rotational terms in their equation of motion. These terms are negligible in low Reynolds number flows such as those encountered here. In our case, the use of PFF would be detrimental, as the contact of droplets with the walls may lead to unwanted wetting effects.