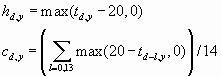
[Posted as supplied by the author]

Statistical methods

We first computed counts, for each day d=1,…,244 up to 31 August of each year y=1996,…,2000, of deaths Y_v,d,y, and total persons n_v,d,y under observation. These were subdivided according to whether the subject was vaccinated (v=1) or not (v=0) in the four months before day 1 of year y, and linked to the count of circulating influenza the previous week, x_d,y, and daily measures (means across UK regions) of temperature. Because cold and hot weather have been found to have prompt and delayed adverse effects respectively, we then calculated for each day, a heat variable h and cold variable c as follows:

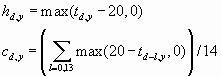
The death counts were then regressed (using a Poisson regression model) on circulating influenza, with the temperature and other potentially confounding variables included to separate an influenza effect from an effect of cold weather:

Primary interest is in the parameters b _u and b _v, the increase in log mortality per unit increase in circulating influenza in the unvaccinated and vaccinated respectively, and the difference between them. For interpretability, circulating influenza was scaled so that one unit is equal to 90^th percentile of circulating influenza. The parameters g _c and g _h represent cold and heat effects, and the 39 parameters i_m (m=2,…,40; where 1 is January 1996 and 40 is August 2000) allow for otherwise unmodelled month-to-month variation. The parameter a _v allows for mortality to be different in vaccinated and unvaccinated persons outside periods of circulating influenza. Such differences are possible due to factors influencing selection for vaccination. Finally, the parameter g _dv allows for difference in mortality between vaccinated and unvaccinated to change linearly with time from the date that they were vaccinated., allowing for a reduction in the selection effect over time.

The model does not include mortality risk factors that do not change with time (smoking, age at baseline, etc). These time-fixed factors are not associated with the index of circulating influenza, which varies over time but not over subjects. They therefore do not confound the parameters of association of circulating influenza with mortality, b _u and b _v, unless the factors affect not only annual mortality but also the short-term variation of mortality over time, in particular in association with circulating influenza. In fact age was very similar in the vaccinated (mean 83.6) and unvaccinated (mean 83.4), so age would not confound a vaccination effect even if it were associated with variations of mortality over time, for example because it affected case fatality rates.

Estimates of b _u and b _v were used to estimate the fraction of mortality at the 90^th percentile of circulating influenza attributable to influenza, and hence an estimate of vaccine effectiveness:

Because this estimate of VE is a non-linear function of the Poisson regression model coefficients of b _u and b _v, we calculated a confidence interval using a parametric bootstrap. Specifically, 10,000 values for VE were calculated from randomly generated values of b _u and b _v assumed to follow normal distributions with means, standard deviations, and correlations taken from the Poisson model estimates. Confidence limits for VE were taken as the 2.5 and 97.5 percentiles of the distribution of simulated VE values, truncated at 0% and 100%.