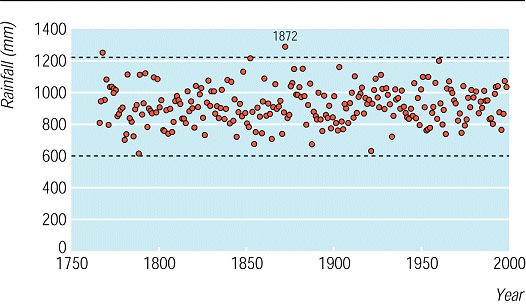
(F1) Fig A Control chart showing annual rainfall in England and Wales during 1766-1999
Text for web only
Constructing control charts
The first step in constructing control charts is ensuring that all providers (such as the 37 hospitals in figs 2 and 3) comprise parts of the same single system. The use of control charts over several evaluation cycles allows us to check whether the single system premise is true. If it is not, hospitals can be regrouped into different systems.
The second step is ensuring that all providers have high quality monitoring systems, with standardised data collection. Providers that are not able to comply with this standard should not be included in the performance monitoring exercise.
The third step is the calculation of control limits. Suitable limits, like the limits set for any diagnostic test, must balance the disadvantages of erroneously concluding that a special cause is present when it is not (the clinical equivalent of a false positive diagnosis) and the disadvantages of failing to detect the presence of a special cause (false negative result). Years of experience from industry have shown that control limits with high specificity are the most appropriate.w1 Experience gained from the health service also suggests that, where the prevalence of a condition is low (as far as we know truly poor performance among NHS providers is rare), the consequences of inappropriate intervention are serious, and the cost of intervention is high, a test with high specificity is appropriate.w2
Constructing control limits
Control limits may be drawn in two ways.
Eyeballing—When many readings are available eyeballing has been shown to be successful for constructing control limits. Figure A shows over 200 readings of the annual rainfall in the United Kingdom since 1766. Most readers, if asked to sketch in upper and lower control limits for normal rainfall, would draw lines close to those shown (range 600-1220 mm/year). All would agree that 1872 was a wet year.

(F1) Fig A Control chart showing annual rainfall in England and Wales during 1766-1999
Statistical—When fewer readings are available the eyeball method becomes somewhat arbitrary. In such circumstances the estimated point performance of the system is calculated from the pooled performance data of all providers. An assumption is now made about the distribution of the performance parameter. Performance limits are then calculated using a specific 3-s test criterion (equivalent to 98.8%). When these rules are applied to binomial performance data such as "proportion of patients who die within 30 days" these control limits are the same as the conventional 99.8% confidence intervals.
Read all Rapid Responses