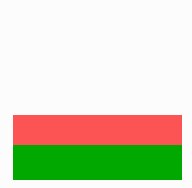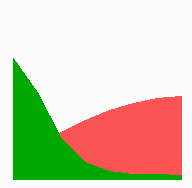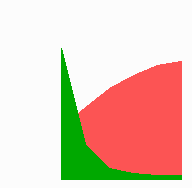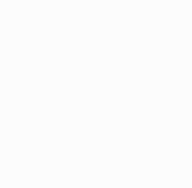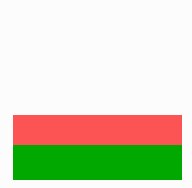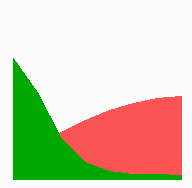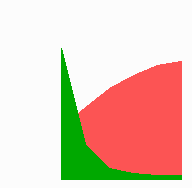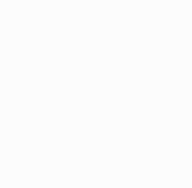Formation of Stable Patterns by Local Autocatalysis and Depletion of a Long-Ranging Substrate
Assumed is a substance that feeds back to increase its own concentration (activator, green). In these examples, this local autocatalysis is balanced by the depletion of a substrate (red) required for the autocatalytic reaction (the activator-inhibitor reaction is described further below). In E. coli, this substrate can correspond to precursor molecules not yet bound to the membrane. It is assumed that this substrate diffuses rapidly. In a region that has an extension comparable with the range of the activator (i.e., in fields much smaller than the range of the substrate), only a single maximum is generated at one marginal position. Minute fluctuations are sufficient to initiate patterning formation [Gierer, A. & Meinhardt, H. (1972) Kybernetik 12, 30-39 (a copy in PDF format can be downloaded at www.eb.tuebingen.mpg.de/abt.4/meinhardt/theory.html)]. After the removal of the activated region, the substrate concentration rises steeply in the remaining field, causing the polar pattern to regenerate: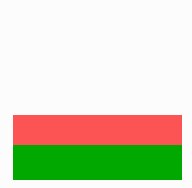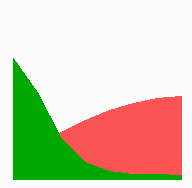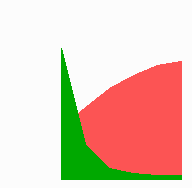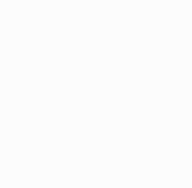
In a somewhat larger field, only symmetrical patterns are possible with either a maximum at each end or a single maximum in the center. The left figure shows the initial condition, two intermediate conditions, and the final pattern (equations and parameters):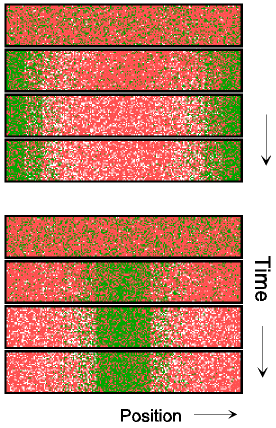

In small but growing fields, a marginal maximum forms first. Upon further growth, the substrate concentration in the nonactivated part increases. The substrate concentration at the flank of the maximum can become so high that the autocatalysis proceeds there more rapidly than in the center of the maximum. The position of the peak becomes unstable and shifts to the center. For the same reason, a maximum splits into two, and so on, during further growth: 
In contrast, if the antagonistic reaction results from an inhibitor that is produced under activator control, periodic patterns form by the insertion of new maxima into the enlarging interstices rather than by the splitting of existing maxima [see Insertion of New Maxima; for more details of this behavior, see Meinhardt, H. (1998) The Algorithmic Beauty of Sea Shells, (Springer, Berlin) 2nd Ed.