Abstract
Purpose:
To improve the accuracy of CT number mapping inside the lung in deformable image registration with large differences in lung volume for applications in vertical CT imaging and adaptive radiotherapy.
Methods:
The deep inspiration breath hold (DIBH) CT image and the end of exhalation (EE) phase image in 4DCT of 14 thoracic cancer patients were used in this study. Lung volumes were manually delineated. A Demons-based deformable registration was first applied to register the EE CT to the DIBH CT for each patient, and the resulting deformation vector field deformed the EE CT image to the DIBH CT space. Given that the mass of the lung remains the same during respiration, we created a mass-preserving model to correlate lung density variations with volumetric changes, which were characterized by the Jacobian derived from the deformation field. The Jacobian determinant was used to correct the lung CT numbers transferred from the EE CT image. The absolute intensity differences created by subtracting the deformed EE CT from the DIBH CT with and without density correction were compared.
Results:
The ratio of DIBH CT to EE CT lung volumes was 1.6 on average. The deformable registration registered the lung shape well, but the appearance of voxel intensities inside the lung was different, demonstrating the need for density correction. Without density correction, the mean and standard deviation of the absolute intensity difference between the deformed EE CT and the DIBH CT inside the lung were 54.5 ± 45.5 for all cases. After density correction, these numbers decreased to 18.1 ± 34.9, demonstrating greater accuracy. The cumulative histogram of the intensity difference also showed that density correction improved CT number mapping greatly.
Conclusion:
Density correction improves CT number mapping inside the lung in deformable image registration for difficult cases with large lung volume differences.
Keywords: Deformable image registration, Jacobian, lung cancer, density correction
1. Introduction
The use of a vertical (seated) position to deliver radiation therapy to thoracic cancer patients has shown advantages in reducing the amount of irradiated lung and reducing tumor motion, as lung volume has been reported to increase and lung motion has been reported to decrease in the seated position compared with lying down.1–4 Vertical treatment may benefit certain patient groups, such as patients with compromised lung function for whom the vertical position is more comfortable,5 patients who are unable to lie down, and patients who have to sit up halfway through their irradiation owing to rapid accumulation of saliva.
Vertical treatment requires taking computed tomography (CT) images in the vertical position for treatment planning. Although several vertical CT systems exist,5–8 they are specialized and are not available in most clinical settings. One existing solution is to use the on-board imager of a common medical linear accelerator to take vertical cone-beam CT (CBCT) images, which can be implemented by programming the Varian TrueBeam linear accelerator in developer mode and rotating the patient couch.9 However, the vertical CBCT images generated in this way cannot produce reliable CT numbers. Previous studies showed that deformable image registration can be used to map the CT numbers from a simulation CT to a CBCT to correct the CT numbers for head and neck and prostate sites,10, 11 which suggests that deformable registration can be used to transfer the CT numbers of an image in a supine position to correct the CT numbers in the vertical CBCT. However, this process is extremely challenging for the thoracic site because of the large changes in patient geometry and lung volume between the supine and vertical scanning positions. Direct mapping of the CT numbers from a supine image to a vertical image may not produce accurate CT numbers because of lung density changes.
In this study, we propose a novel density correction technique as a post-processing step for deformable image registration to achieve accurate CT number mapping at the thoracic site in the presence of large deformation of the lung. This approach was developed on the basis of physics principles in CT imaging. Vertical treatment may result in treatment plans similar to those for deep inspiration breath hold (DIBH) treatment; therefore, the vertical CT image with correct CT numbers was simulated by a DIBH CT image.4 To represent the large lung deformation between the vertical and supine scanning positions, the supine CT image was simulated by the end of exhalation (EE) phase image in a 4DCT scan. The CT numbers of the EE image were deformably mapped to the DIBH image, and the density correction technique was applied to correct the CT number mapping inside the lung (Figure 1). We then validated our proposed density correction approach by comparing the corrected and uncorrected results.
Figure 1.
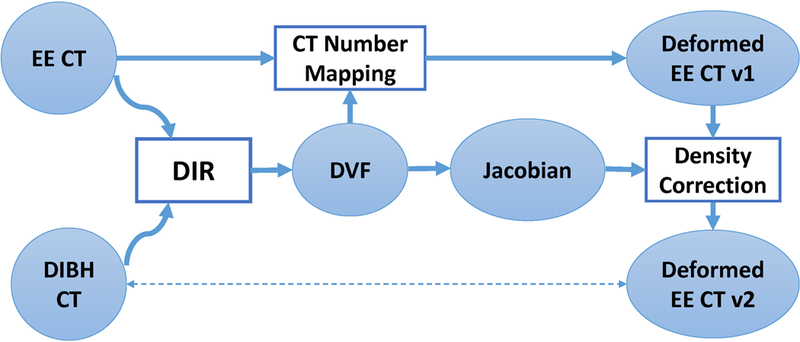
Overall framework of our proposed approach. Deformable image registration (DIR) was used to register end of exhalation (EE) CT to deep inspiration breath hold (DIBH) CT. The resultant deformation vector field (DVF) was then used to map the CT numbers from the EE CT to the DIBH CT space, resulting in deformed EE CT v1. At the same time, Jacobian was calculated from the DVF and used to correct the CT numbers inside the lung for the deformed EE CT v1, resulting in deformed EE CT v2, which improved the accuracy of the CT numbers.
2. Materials and Methods
2.1. Patient data
We retrospectively identified and included 14 patients with lung cancer who had both a DIBH scan and a 4DCT scan on the same day and were treated with stereotactic body radiotherapy during November 2007 through July 2009 at The University of Texas MD Anderson Cancer Center. The treatment plan had been created used the DIBH CT, and the total lung contours had been manually drawn on the DIBH CT in the Pinnacle treatment planning system (Philips Medical Systems, Fitchburg, WI). When contouring the lung, tumor and high density vessels were excluded. Both the DIBH CT and the EE CT had a resolution of 1 mm × 1 mm × 2.5 mm. This study was approved by the institutional review board of MD Anderson Cancer Center.
2.2. Deformable image registration
We performed the EE-to-DIBH deformable registration using an intensity-based dual-force Demons algorithm as previously described by Wang et al. 12 The EE and DIBH Images were separated into small block and histogram equalization was performed on each block before registration and a multi-resolution scheme was used to accelerate the registration. The parameters for the deformable registration are specified in Table 1. The deformation vector field generated from the deformable registration was used to map the CT numbers of the EE CT to the spatial domain of the DIBH CT, generating a deformed EE CT.
Table 1.
Parameter settings for the deformable image registration
| Parameter | Value |
|---|---|
| Number of bins for histogram equalization | 256 |
| Block size for histogram equalization | 20 |
| Multi-resolution levels | 6 |
| Maximum number of iterations | 200 |
| Upper bound of step size | 1.25 |
| Gaussian variance for regularization | 1.5 |
2.3. Mass-preserving model
Our density correction technique is based on the assumption that the mass of the air flowing into the lung is negligible compared with the average mass of the human lungs13–15; therefore, the mass of the lungs remains approximately the same between the EE and DIBH states. Mathematically, let denote the mapping function at coordinate from the DIBH CT to the EE CT, and let the deformation vector obtained from the aforementioned deformable registration be . The deformable mapping function can be characterized as
| (1) |
Let denote the lung density at on the DIBH CT, and let denote the lung density at on the EE CT. The mass-preserving model renders the following equation:
| (2) |
where denotes the entire lung volume on the DIBH CT and approximates the lung volume of the EE CT, assuming that the deformable registration correctly maps the lung volume boundary from the DIBH CT to the EE CT. denotes the mass of the air inhaled at DIBH, also known as the tidal volume. The value of at DIBH isnormally about 1–3 g.16 Compared with the average mass of the human lungs (~700 g),17, 18 the mass of the inhaled air is negligible. Therefore, can be left out of Equation 2. Furthermore, by the introduction of the Jacobian of the deformation vector field, , Equation 2 is converted to
| (3) |
where denotes the Jacobian determinant at location ,
| (4) |
Over an infinitesimal volume, we can obtain the following equation from Equation 3:
| (5) |
2.4. Density correction
The determinant of Jacobian, , indicates the volume change from DIBH CT to EE CT at a voxel level. A value equal to 1 indicates no volume change at a voxel location , while a value less than 1 indicates volume shrinkage and a value greater than 1 indicates volume expansion at that voxel. From the physics of CT imaging, we know that the CT number is proportional to the tissue density.19 Therefore, Equation 5 can be rewritten as
| (6) |
where denotes the Hounsfield units, or CT number. The deformable registration maps coordinate on the DIBH CT to the location on the EE CT and transfers the CT number on the DIBH CT at to the on EE CT. Equation 6 indicates that the mapped CT number needs a proper correction using the Jacobian determinant,. When the volume change is small, with , this density correction can be neglected. However, if the volume change is large, the correction becomes very important in accurately mapping the CT numbers. The density correction approach was applied to all 14 patients after deformable registration mapping of the CT numbers from EE CT to the DIBH CT. For validation, we compared the differences in CT numbers between the deformed EE CT and the DIBH CT voxel by voxel before and after density correction. The absolute intensity difference was plotted as a histogram to show the distribution of values with and without density correction.
3. Results
The lung contours on the DIBH CT were deformably mapped to the EE CT using the deformable registration. The deformed lung contours on the EE CT were visually checked for all 14 patients to ensure correct contour mapping and then imported into the Pinnacle treatment planning system for volume measurement. The lung volumes on both DIBH CT and EE CT for all 14 patients are shown in Table 2. For all patients, the mean absolute volume difference between DIBH CT and EE CT was 2046 cc, and the mean volume ratio of DIBH CT to EE CT was 1.6, representing a large lung volume difference between DIBH and EE states. For one representative patient, a Jacobian map inside the lung (Figure 2) shows large volume changes at a voxel level calculated from the deformation vector field, demonstrating the need for density correction to correctly map the CT numbers from one lung state to the other using deformable registration.
Table 2.
Lung volumes in both lung states for all patients. The lung volume in the deep inspiration breath hold state is much greater than that in the end of exhalation state .
| Patient No. | (cc) | (cc) | Absolute difference (cc) |
Volume ratio |
|---|---|---|---|---|
| 1 | 6021.8 | 3643.8 | 2378.0 | 1.65 |
| 2 | 6351.3 | 3459.7 | 2891.6 | 1.84 |
| 3 | 7391.8 | 3734.5 | 3657.3 | 1.98 |
| 4 | 5508.5 | 3397.3 | 2111.2 | 1.62 |
| 5 | 4460.3 | 2807.9 | 1652.4 | 1.59 |
| 6 | 5287.1 | 3109.8 | 2177.3 | 1.70 |
| 7 | 6246.5 | 4214.8 | 2031.7 | 1.48 |
| 8 | 7311.1 | 6055.4 | 1255.7 | 1.21 |
| 9 | 3428.8 | 2637.0 | 791.8 | 1.30 |
| 10 | 6814.6 | 4959.1 | 1855.5 | 1.37 |
| 11 | 4877.4 | 3222.3 | 1655.1 | 1.51 |
| 12 | 4066.6 | 2591.9 | 1474.7 | 1.57 |
| 13 | 4802.7 | 2518.3 | 2284.4 | 1.91 |
| 14 | 5514.1 | 3091.7 | 2422.4 | 1.78 |
| Mean ± standard deviation | 5577.3 ± 1189.8 | 3531.7 ± 986.5 | 2045.7 ± 707.6 | 1.61 ± 0.22 |
Figure 2.
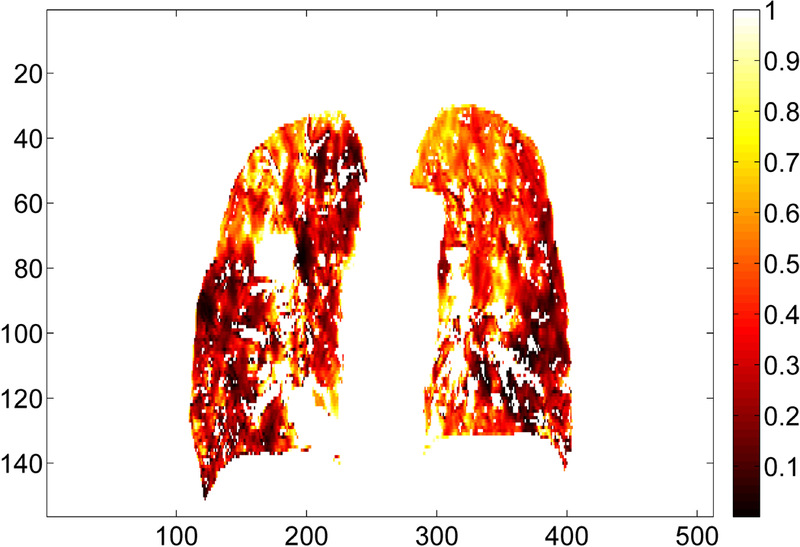
Illustration of the Jacobian map inside the lung for one representative patient (Patient 3 from Table 1) in coronal view. The deformation vectors are from the deep inspiration breath hold CT to the end of exhalation CT. All the Jacobian values are less than 1, indicating a volume shrinkage. Jacobian values for the tumor and the high-density vessels are excluded from this illustration.
The mean CT numbers inside the lungs for both DIBH CT and EE CT and the absolute difference between the CTs are shown in Table 3. Because the DIBH CT was taken with more air inside the lung, the DIBH CT had much lower CT numbers than the EE CT did. After deformable image registration, the CT number differences between the deformed EE CT and the DIBH CT showed that the density correction greatly improved the accuracy of the CT numbers: the mean CT number difference for all 14 patients decreased from 54.5 ± 45.5 (before density correction) to 18.1 ± 34.9 (after density correction). Figure 3 illustrates the deformed EE CT image before and after density correction compared with the DIBH CT image in one patient. The histogram of absolute intensity differences at the voxel level before and after density correction for the same patient shows that the density correction significantly reduced the CT number differences between the deformed EE CT and DIBH CT (Figure 4). Although the accuracy of CT number is improved, we do noticed that the image after density correction may not appear naturally, indicating a voxel-level operation in density correction.
Table 3.
Mean Hounsfield units (HU) inside the lung for the deep inspiration breath hold (DIBH) state, or , and for the end of exhalation (EE) state, or , and the absolute difference between them, followed by the HU difference (mean ± standard deviation) of deformable image registration both before and after density correction.
| Patient no. | HU difference before density correction |
HU difference after density correction |
|||
|---|---|---|---|---|---|
| 1 | −817 | −702.5 | 114.5 | 58.9 ± 48.3 | 17.7 ± 34.7 |
| 2 | −827.3 | −671.1 | 156.2 | 63.7 ± 48.1 | 16.2 ± 34.1 |
| 3 | −804 | −627.1 | 176.9 | 67.9 ± 42.2 | 12 ± 28.6 |
| 4 | −834.7 | −765.6 | 69.1 | 49.3 ± 52.1 | 22.6 ± 40.8 |
| 5 | −831.5 | −735.4 | 96.1 | 60.7 ± 42.6 | 21 ± 37.2 |
| 6 | −835.5 | −711.8 | 123.7 | 65.0 ± 56.8 | 24.1 ± 42.6 |
| 7 | −791.7 | −702.4 | 89.3 | 51.4 ± 44.8 | 16.4 ± 32.5 |
| 8 | −840 | −796.4 | 43.6 | 33.8 ± 39.6 | 20.8 ± 37.2 |
| 9 | −825.4 | −780.4 | 45 | 39.4 ± 40.3 | 19.6 ± 34.5 |
| 10 | −708.4 | −611.4 | 97 | 50.5 ± 41.6 | 15.7 ± 31.7 |
| 11 | −818.6 | −726.5 | 92.1 | 50.0 ± 54.7 | 23.4 ± 42.5 |
| 12 | −716 | −588.5 | 127.5 | 46.3 ± 34.6 | 9.8 ± 23.2 |
| 13 | −875.3 | −773.8 | 101.5 | 66.6 ± 45.5 | 18.4 ± 36.1 |
| 14 | −850.7 | −741.2 | 109.5 | 59.7 ± 45.8 | 15.9 ± 33.5 |
| Mean | −812.6 | −709.6 | 103 | 54.5 ± 45.5 | 18.1 ± 34.9 |
Figure 3.
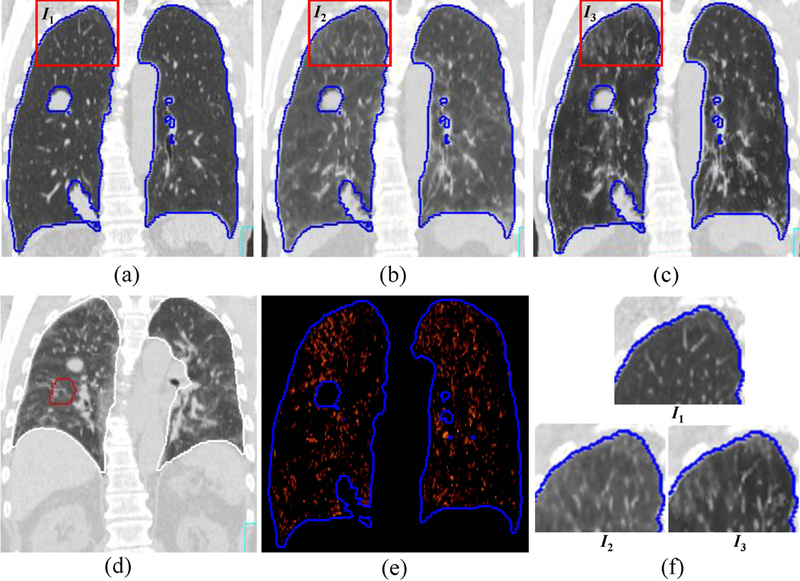
Illustration of the difference in CT number mapping before and after density correction for one patient (patient no. 3 in Table 2). (a) Deep inspiration breath hold (DIBH) CT; (b) deformed end of exhalation (EE) CT before density correction; (c) deformed EE CT after density correction; (d) EE CT before deformation; (e) The difference inside the lung between (a) and (c); (f) The zoom-in of the rectangular regions in (a), (b), and (c). The CT numbers inside the lung on the deformed EE CT after density correction (c) are much closer to those of the DIBH CT (a) than are those of the deformed EE CT without density correction (b).
Figure 4.
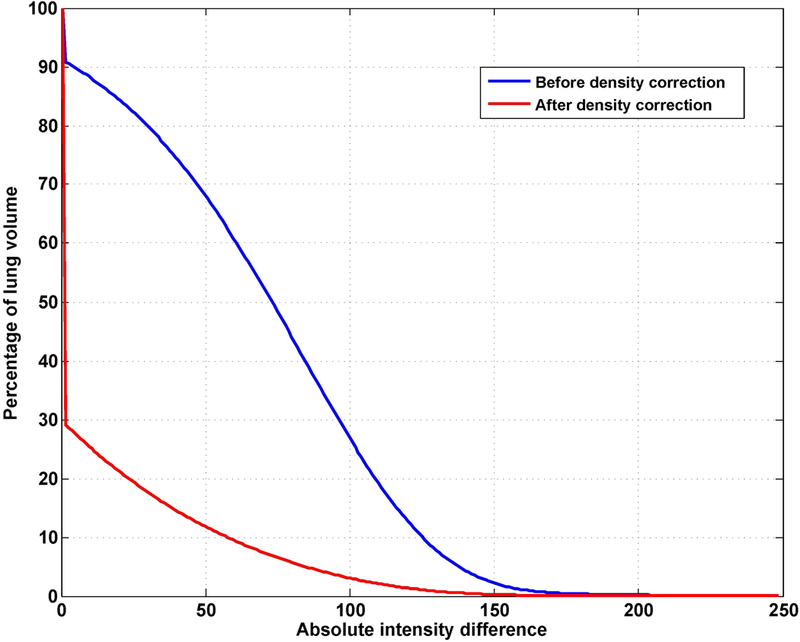
Cumulative histogram of absolute intensity differences between the DIBH CT and deformed EE CT inside the lung for the patient shown in Figure 3. The error after density correction (red line) is significantly reduced compared with the error before density correction (blue line).
4. Discussion
We have developed a novel density correction technique as a post-processing step for deformable image registration and have validated its efficacy in achieving accurate CT number mapping at the thoracic site in the presence of large lung deformation. Our approach is different from previous approaches using a mass-preserving model in deformable registration14, 15 in that we focused on the correction of CT numbers for subsequent applications of the deformed images. The major application of our approach is to correct the CT numbers for CBCT images by using the information from planning CT. In practice, our approach could be easily implemented in vertical treatment (if necessary) or adaptive radiotherapy.
Treating patients in a seated position, though it is not popular, could benefit certain patient groups.4, 5 Physicians at our institution expressed interest in the use of a seated treatment position for patients who are not able to tolerate normal, supine treatment positioning. Besides the aforementioned comfort and dosimetric advantages, vertical treatment has allowed for the development of a treatment paradigm centered on a fixed treatment beam and a rotating seated patient.20 Researchers have investigated the potential advantages and feasibility of this fixed-beam cancer radiotherapy. This treatment approach can be used to develop a low-cost linear accelerator system that benefits low- and middle-income countries. 20–22
The feasibility of using CBCT for dose calculation to generate an adaptive plan has been investigated over the past decade.23–25 For CBCT to be used for dose calculation, the CT numbers must be accurate. One approach to generate accurate CT numbers is using deformable registration (a necessary step in adaptive radiotherapy) to map the CT number in planning CT to the CBCT voxel by voxel. This method has proven effective.26–28 However, for lung cancer patients, our approach showed that deformable mapping of the CT numbers alone is not enough. This finding agrees with those of Marchant et al., who found that deformable registration to correct the CT numbers for CBCT resulted in larger dose calculation error for lung images than for pelvis and head and neck images.27 Our density correction technique to produce accurate CT numbers for CBCT could improve the accuracy of this dose calculation.
The major limitation of the proposed approach is that the density correction could only be applied to the area with volume change due to air, where the air mass can be neglected. Essentially, this technique can only be applied to lung CT images, and the lung volume should be delineated before the approach can be applied. Existing auto-segmentation tools29 could be used for lung auto-delineation, but the tumor and high density vessels should be properly excluded from the lung region because they should not be corrected for density. The deep learning approaches29 are promising in achieving this goal, but a visual check of the lung contours are recommended before proceeding to density correction. When checking the lung contours, we suggest following the RTOG 1106 contouring guideline.30 Also, the effectiveness of this approach is limited by the accuracy of deformable image registration. Not only the deformable registration determines the spatial mapping from one image to the other, but also the density correction relies on the deformation vector field generated by deformable registration. We chose the dual-force Demons registration algorithm because we have fully validated this algorithm for 4DCT registration. In our previous report,31 the algorithm achieved a mean registration accuracy of 1.29 mm on 10 4DCT datasets from DIR-Lab (http://dir-lab.com). The result is similar to or better than those reported by other researchers at the DIR-Lab web site. However, due to the difference in CT numbers, the similarity measure using sum of squared differences in the Demons registration algorithm may not be optimal. Other registration algorithms using cross-correlation or mutual information metrics can be considered as alternatives.32, 33 Last, although we know that improved CT number accuracy will improve dose calculation in treatment plans, how much of the CT number error will carry over to the dose calculation is still unknown. Treatment planning using the density correction technique will be the subject of our future study.
5. Conclusions
We propose a density correction approach as a post-processing step for deformable image registration to improve the CT number mapping inside the lung for difficult cases that have large lung volume differences. We validated the approach in thoracic patients by showing an improvement in CT number accuracy after density correction. This density correction technique has the potential to vertical treatment and adaptive radiotherapy.
Acknowledgments:
This work was support in part by the CPRIT (Cancer Prevention Research Institute of Texas) grant RP110562 and the National Institutes of Health through Cancer Center Support Grant P30CA016672. The authors would like to thank Ms. Sarah Bronson from Department of Scientific Publications for reviewing this manuscript.
Footnotes
Conflict of Interest: The authors have no conflicts to disclose.
Meeting presentations: This work was partially presented at the 56th American Association of Physicists in Medicine meeting in July 2014.
References
- 1.Takazakura R, Takahashi M, Nitta N, Murata K, “Diaphragmatic motion in the sitting and supine positions: Healthy subject study using a vertically open magnetic resonance system,” Journal of Magnetic Resonance Imaging 19, 605–609 (2004). [DOI] [PubMed] [Google Scholar]
- 2.Duisters C, Beurskens H, Nijsten S, Starmans M, Wanders S, Verschueren T, Lambin P, Minken A, De Ruysscher D, “Palliative chest irradiation in sitting position in patients with bulky advanced lung cancer,” Radiotherapy and Oncology 79, 285–287 (2006). [DOI] [PubMed] [Google Scholar]
- 3.Klein EE, Hanley J, Bayouth J, Yin F-F, Simon W, Dresser S, Serago C, Aguirre F, Ma L, Arjomandy B, Liu C, Sandin C, Holmes T, “Task Group 142 report: Quality assurance of medical accelerators,” Medical Physics 36, 4197–4212 (2009). [DOI] [PubMed] [Google Scholar]
- 4.Yang J, Chu D, Dong L, Court LE, “Advantages of simulating thoracic cancer patients in an upright position,” Pract Radiat Oncol 4, e53–58 (2014). [DOI] [PubMed] [Google Scholar]
- 5.Miller RW, Raubitschek AA, Harrington FS, van de Geijn J, Ovadia J, Glatstein E, “An isocentric chair for the simulation and treatment of radiation therapy patients,” Int J Radiat Oncol Biol Phys 21, 469–473 (1991). [DOI] [PubMed] [Google Scholar]
- 6.Shah AP, Strauss JB, Kirk MC, Chen SS, Kroc TK, Zusag TW, “Upright 3D treatment planning using a vertical CT,” Medical dosimetry : official journal of the American Association of Medical Dosimetrists 34, 82–86 (2009). [DOI] [PubMed] [Google Scholar]
- 7.Klein EE, Wasserman T, Ermer B, “Clinical introduction of a commercial treatment chair to facilitate thorax irradiation,” Medical Dosimetry 20, 171–176 (1995). [DOI] [PubMed] [Google Scholar]
- 8.Boag JW, Hodt HJ, “Adjustable chair for radiotherapy of head and neck cancer,” The British journal of radiology 44, 316–317 (1971). [DOI] [PubMed] [Google Scholar]
- 9.Fave X, Yang J, Carvalho L, Martin R, Pan T, Balter P, Court L, “Upright cone beam CT imaging using the onboard imager,” Med Phys 41, 061906 (2014). [DOI] [PubMed] [Google Scholar]
- 10.van Zijtveld M, Dirkx M, Heijmen B, “Correction of conebeam CT values using a planning CT for derivation of the “dose of the day”,” Radiother Oncol 85, 195–200 (2007). [DOI] [PubMed] [Google Scholar]
- 11.van Zijtveld M, Dirkx M, Breuers M, Kuipers R, Heijmen B, “Evaluation of the ‘dose of the day’ for IMRT prostate cancer patients derived from portal dose measurements and cone-beam CT,” Radiother Oncol 96, 172–177 (2010). [DOI] [PubMed] [Google Scholar]
- 12.Wang H, Dong L, Lii MF, Lee AL, de Crevoisier R, Mohan R, Cox JD, Kuban DA, Cheung R, “Implementation and validation of a three-dimensional deformable registration algorithm for targeted prostate cancer radiotherapy,” International Journal of Radiation Oncology*Biology*Physics 61, 725–735 (2005). [DOI] [PubMed] [Google Scholar]
- 13.Yin YB, Hoffman EA, Lin CL, “Mass preserving nonrigid registration of CT lung images using cubic B-spline,” Medical Physics 36, 4213–4222 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Haker S, Tannenbaum A, Kikinis R, “Mass Preserving Mappings and Image Registration,” in Medical Image Computing and Computer-Assisted Intervention – MICCAI 2001: 4th International Conference Utrecht, The Netherlands, October 14–17, 2001 Proceedings, edited by Niessen WJ, Viergever MA (Springer; Berlin Heidelberg, Berlin, Heidelberg, 2001), pp. 120–127. [Google Scholar]
- 15.Gorbunova V, Sporring J, Lo PC, Loeve M, Tiddens HA, Nielsen M, Dirksen A, de Bruijne M, “Mass preserving image registration for lung CT,” Medical Image Analysis 16, 786–795 (2012). [DOI] [PubMed] [Google Scholar]
- 16.Barrett K, Brooks H, Boitano S, Barman S, Ganong’s review of medical physiology, 23rd Edition ed. (McGraw-Hill Medical, New York, 2010). [Google Scholar]
- 17.Molina DK, DiMaio VJ, “Normal organ weights in men: part II-the brain, lungs, liver, spleen, and kidneys,” Am J Forensic Med Pathol 33, 368–372 (2012). [DOI] [PubMed] [Google Scholar]
- 18.Molina DK, DiMaio VJ, “Normal Organ Weights in Women: Part II-The Brain, Lungs, Liver, Spleen, and Kidneys,” Am J Forensic Med Pathol 36, 182–187 (2015). [DOI] [PubMed] [Google Scholar]
- 19.Bushberg JT, Seibert JA, Leidholdt EM Jr, Boone JM, The Essential Physics of Medical Imaging, Second Edition ed. (Lippincott Williams & Wilkins, Philadelphia, PA, 2002). [Google Scholar]
- 20.McCarroll RE, Beadle BM, Fullen D, Balter PA, Followill DS, Stingo FC, Yang JZ, Court LE, “Reproducibility of patient setup in the seated treatment position: A novel treatment chair design,” Journal of Applied Clinical Medical Physics 18, 223–229 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.McCarroll R, Youssef B, Beadle B, Bojador M, Cardan R, Famiglietti R, Followill D, Ibbott G, Jhingran A, Trauernicht C, Balter P, Court L, “Model for Estimating Power and Downtime Effects on Teletherapy Units in Low-Resource Settings,” Journal of Global Oncology 3, 563–571 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Feain I, Coleman L, Wallis H, Sokolov R, O’Brien R, Keall P, “Technical Note: The design and function of a horizontal patient rotation system for the purposes of fixed-beam cancer radiotherapy,” Med Phys 44, 2490–2502 (2017). [DOI] [PubMed] [Google Scholar]
- 23.Veiga C, Lourenco AM, Mouinuddin S, van Herk M, Modat M, Ourselin S, Royle G, McClelland JR, “Toward adaptive radiotherapy for head and neck patients: Uncertainties in dose warping due to the choice of deformable registration algorithm,” Medical Physics 42, 760–769 (2015). [DOI] [PubMed] [Google Scholar]
- 24.Duffton A, Harrow S, Lamb C, McJury M, “An assessment of cone beam CT in the adaptive radiotherapy planning process for non-small-cell lung cancer patients,” British Journal of Radiology 89 2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Guan HQ, Dong H, “Dose calculation accuracy using cone-beam CT (CBCT) for pelvic adaptive radiotherapy,” Physics in Medicine and Biology 54, 6239–6250 (2009). [DOI] [PubMed] [Google Scholar]
- 26.Zhang Y, Yang J, Zhang L, Court LE, Gao S, Balter PA, Dong L, “Digital reconstruction of high-quality daily 4D cone-beam CT images using prior knowledge of anatomy and respiratory motion,” Comput Med Imaging Graph 40, 30–38 (2015). [DOI] [PubMed] [Google Scholar]
- 27.Marchant TE, Joshi KD, Moore CJ, “Accuracy of radiotherapy dose calculations based on cone-beam CT: comparison of deformable registration and image correction based methods,” Physics in Medicine and Biology 63, 065003 (065012pp) (2018). [DOI] [PubMed] [Google Scholar]
- 28.Moteabbed M, Sharp GC, Wang Y, Trofimov A, Efstathiou JA, Lu HM, “Validation of a deformable image registration technique for cone beam CT-based dose verification,” Medical Physics 42, 196–205 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Yang J, Veeraraghavan H, Armato SG 3rd, Farahani K, Kirby JS, Kalpathy-Kramer J, van Elmpt W, Dekker A, Han X, Feng X, Aljabar P, Oliveira B, van der Heyden B, Zamdborg L, Lam D, Gooding M, Sharp GC, “Autosegmentation for thoracic radiation treatment planning: A grand challenge at AAPM 2017,” Med Phys 45, 4568–4581 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Atlases for Organs at Risk (OARs) in Thoracic Radiation Therapy, https://www.rtog.org/CoreLab/ContouringAtlases/LungAtlas.aspx
- 31.Zhang Y, Yang J, Zhang L, Court LE, Balter PA, Dong L, “Modeling respiratory motion for reducing motion artifacts in 4D CT images,” Medical Physics 40, 041716 (2013). [DOI] [PubMed] [Google Scholar]
- 32.Dong L, Yang J, Zhang Y, “Image Processing in Adaptive Radiotherapy,” in Image Processing in Radiation Therapy, edited by Brock K (CRC Press, Boca Raton, FL, 2013), pp. 3–20. [Google Scholar]
- 33.Brock KK, Mutic S, McNutt TR, Li H, Kessler ML, “Use of image registration and fusion algorithms and techniques in radiotherapy: Report of the AAPM Radiation Therapy Committee Task Group No. 132,” Medical Physics, (2017). [DOI] [PubMed] [Google Scholar]


