Independent recalculation outperforms traditional measurement-based IMRT QA methods in detecting unacceptable plans

Abstract

Purpose:

To evaluate the performance of an independent recalculation and compare it against current measurement-based patient specific intensity-modulated radiation therapy (IMRT) quality assurance (QA) in predicting unacceptable phantom results as measured by the Imaging and Radiation Oncology Core (IROC).

Methods:

When institutions irradiate the IROC head and neck IMRT phantom, they are also asked to submit their internal IMRT QA results. Separately from this, IROC has previously created reference beam models on the Mobius3D platform to independently recalculate phantom results based on the institution’s DICOM plan data. The ability of the institutions’ IMRT QA to predict the IROC phantom result was compared against the independent recalculation for 339 phantom results collected since 2012. This was done to determine the ability of these systems to detect failing phantom results (i.e., large errors) as well as poor phantom results (i.e., modest errors). Sensitivity and specificity were evaluated using common clinical thresholds, and ROC curves were used to compare across different thresholds.

Results:

verall, based on common clinical criteria, the independent recalculation was 12 times more sensitive at detecting unacceptable (failing) IROC phantom results than clinical measurement-based IMRT QA. The recalculation was superior, in head-to-head comparison, to the EPID, ArcCheck, and MapCheck devices. The superiority of the recalculation versus these array-based measurements persisted under ROC analysis as the recalculation curve had a greater area under it and was always above that for these array devices. For detecting modest errors (poor phantom results rather than failing phantom results), neither the recalculation nor measurement-based IMRT QA performed well.

Conclusions:

A simple recalculation outperformed current measurement-based IMRT QA methods at detecting unacceptable plans. These findings highlight the value of an independent recalculation, and raise further questions about the current standard of measurement-based IMRT QA.

Introduction

Pre-treatment verification of intensity-modulated radiation therapy (IMRT) dose delivery remains a standard of care for radiotherapy quality assurance. The need for this quality assurance (QA) step is clear in that the accurate delivery of IMRT is challenging; IROC continues to see a failure rate of approximately 10% on its basic head and neck IMRT credentialing phantom.^1,2 This occurs with a 7%/4mm acceptability criterion; the failure rate increases to 23% if a 5%/4mm criteria is used.² Importantly, these errors are overwhelmingly systematic dosimetric errors, where the dose distribution has the correct shape and is in the correct location, but has a systematically wrong magnitude.² This type of dosimetric error would almost certainly impact patients being treated (as opposed to, for example, setup errors or other errors specific to the phantom irradiation).² In short, there remains a clear need for pre-treatment IMRT QA to identify unacceptable plans (i.e., plans that should not be delivered to the patient).

However, traditional measurement-based methods of IMRT QA are suspect. These approaches have come under increasing scrutiny for their inability to detect major and substantial errors in the dose being delivered to the patient.^3–9 Numerous standard measurement-based IMRT QA methods have been found to have poor sensitivity in the identification of low quality or unacceptable IMRT plans. For example, the EPID (Varian Medical Systems, Palo Alto CA) and MatriXX (IBA, Germany) devices both incorrectly indicated that unacceptable plans were as good as, or even better than, acceptable plans.³ Similarly, IMRT QA based on field-by-field MapCheck (SunNuclear, Florida) analysis was unable to detect a problem with a single one of the 15 unacceptable (but clinical) treatment plans delivered to it.⁶ In short, when confronted with unacceptable treatment plans, current measurement-based IMRT QA devices routinely and incorrectly indicate that these plans are adequate. Given that the accuracy of IMRT delivery is still routinely lower than is acceptable and the quality of current IMRT QA is inadequate, the IMRT QA process must be improved.

IROC recently implemented an independent dose recalculation system to evaluate the contribution of dose calculation errors to failing phantom results. With this system, planning system dose calculation errors were found in 68% of failing phantom results.¹⁰ These results indicate that an independent calculation system may, in fact, be well-suited for detecting plan errors, and therefore appropriate for conducting IMRT QA. The testing of this hypothesis was the focus of the current study: how well does an independent recalculation perform as an IMRT QA tool, particularly as compared to current IMRT QA standards. IROC’s independent recalculation, as well as the institution’s own IMRT QA results, were both compared to the actual delivered dose in IROC’s head and neck IMRT phantoms. This comparison allowed a direct evaluation of the independent recalculation system and intercomparison between it and current measurement-based IMRT QA techniques (as implemented in the clinic) to see how well these different processes predict the acceptability of actual dose delivery.

Methods

Phantom

The IROC head and neck phantom is used for the credentialing of NCI-sponsored clinical trials using IMRT.¹¹ When irradiating the IROC phantom, institutions are instructed to treat the phantom like a patient, including scanning it, designing a treatment plan for it, and then delivering the plan. The phantom contains two targets and a nearby organ at risk. The delivered dose is measured in the two targets using a total of 6 thermoluminescent dosimeters (TLD); it is also assessed with a sagittal and axial plane of Gafchromic film (intersecting the center of the primary target). The dose delivered to the phantom is compared to the dose predicted by the treatment planning system. While dose constraints are provided to the institution, the success of the irradiation is based solely on agreement between the measured and calculated doses. To pass, all 6 TLD must agree within ±7% of the calculated dose, and both planes of film must achieve at least 85% of pixels passing a global 7%/4mm gamma criterion (evaluated over a geometric rectangle surrounding the target and avoidance structures). While these criteria have been established for clinical trial credentialing, they are relatively loose compared to established dose precision requirements to achieve the desired outcome (5–7%). Indeed, a recent review of phantom results, including uncertainty analysis in the dosimetry processes used in the phantom, found that 5% dose agreement should be readily achievable on the TLD results.² Therefore, both a 7%/4mm dose and gamma criteria as well as a simple 5% dose criteria were considered in this study. Results outside of 7%/4mm are referred to as failing phantom results, while those with >5% dose discrepancies are referred to as poor phantom results.

Institutional IMRT QA

Upon developing the treatment plan for the phantom, institutions are instructed to conduct and submit their own IMRT QA results based on their clinical practice. This data was submitted by the vast majority of institutions. As part of the current study, IMRT QA results were abstracted for: stated pass/fail status (i.e., did the institution claim that their IMRT QA failed), result (percent agreement or percent of pixels passing gamma), device used for IMRT QA, and criteria (%/mm) used for gamma analysis. No institutions indicated that their plan failed their IMRT QA; however, several submitted IMRT QA results that were poor. Therefore, IROC evaluated the institutional IMRT QA results to determine pass/fail status based on common clinical thresholds. The IMRT QA result was declared to have passed if at least one point dose assessment agreed within 3% or if >90% of pixels passed a composite gamma criteria of 3%/3mm (or tighter). Field-by-field gamma results could have at most one field with <90% of pixels passing and still be declared as passing. The IMRT QA result was declared to have failed if all point dose assessments showed a disagreement of >3% or if <90% of pixels passed a gamma criteria of 3%/3mm (or looser). Results that could not be categorized according to this system (e.g., >90% of pixels passing very loose gamma criteria or <90% of pixels passing very stringent gamma criteria) were excluded from this evaluation.

Independent Recalculation

Independent recalculation was used as a second form of IMRT QA. This process was done by IROC using the Mobius3D platform (Varian Medical Systems, Palo Alto, CA) combined with IROC-developed beam models to recompute treatment plan doses.¹⁰ Treatment plans were recomputed using the institution’s generated DICOM plan, CT dataset, and DICOM structure files. Each recalculation was done using the appropriate IROC beam model: the Varian Base Class,¹² Varian TrueBeam,¹² or Elekta Agility.¹³ Irradiations done with an accelerator that was not represented by one of the aforementioned IROC beam models were not included in this analysis. Similarly, phantom results prior to 2012 were not included because these irradiations predated the DICOM standard. In total, 337 plans were reevaluated using Mobius3D.

Recalculated doses were compared against the original treatment planning system calculations. For most analyses, this comparison was made between the two calculations over the 6 regions of interest in the PTV where the measurements were conducted (i.e., the 6 TLD contours). The worst agreement between the two calculations was used to evaluate whether the recalculation “flagged” the plan. As a starting point, a disagreement in excess of 4% at any one point was taken to indicate a problematic plan (this criteria is was previously used in several studies assessing multiple point dose comparisons^3,6 and is consistent with the criteria typically used for IMRT QA). However, other secondary analysis was also done evaluating the average dose disagreement between the two calculations over the 6 locations in the PTV. Additionally, 3D gamma results over the PTV were examined using a 3%/3mm criteria and a 10% low dose threshold.

Analysis

The ability of IMRT QA (both institutional and independent recalculation) to detect unacceptable IMRT (as measured with the IROC phantom for both cases) was evaluated in three ways:

Sensitivity and specificity:

First, the sensitivity and specificity of institutional IMRT QA as well as IROC’s recalculation system were calculated and compared. Sensitivity is the proportion of unacceptable plans (i.e., the proportion that failed the phantom or, in separate analysis, were poor results) that were correctly flagged as a bad plan by the institution’s IMRT QA process (or IROC’s recalculation system). Specificity is the proportion of plans that passed the phantom (or were good results) that were correctly passed by the institution’s IMRT QA (or IROC’s recalculation system). The sensitivity and specificity were compared for the entire cohort of evaluable plans (337), as well as for subsets based on the main institutional QA devices. When institutions performed QA using multiple devices, a single overall evaluation was made but each device’s performance was also separately interpreted. The significance of differences in the sensitivity and specificity between IMRT QA and the IROC recalculation was assessed using McNemar’s test, which is the appropriate statistical test to compare sensitivity and specificity in paired data, i.e., when the two approaches under comparison are applied to the same set of objects.

Regression analysis:

Sensitivity and specificity assess only the agreement of the binary pass/fail result. We therefore compared the actual numeric values between IMRT QA / IROC recalculation results and the phantom measurement to see if there was a relationship. We compared the percent of pixels passing planar gamma analysis results between IMRT QA and the planar gamma analysis results of the IROC phantom. We also compared the percent of pixels passing gamma analysis between the recalculation and the film results of the IROC phantom. This was done for all cases where institutional results existed (n=299). The percent of pixels passing gamma in the IROC phantom was the average over both film planes (using the 7%/4mm criteria). The percent of pixels passing gamma in the Mobius3D recalculation was a 3D gamma calculated with a 3%/3mm criteria. The institutional IMRT QA result was divided into those results evaluated with a 2%/2mm criteria (n=54) and those with a 3%/3mm criteria (n=245). These were considered as separate cohorts because we could not convert between them based on the submitted data (which only included the final result).

In addition to the gamma results, point dose-based IMRT QA results were evaluated (n=46). The measured point dose difference from the institution’s QA (measured minus treatment planning system [TPS] calculated dose; average point dose if multiple point measurements were reported) were compared against the average of the 6 TLD-measured dose differences in the phantom (measured dose minus TPS-calculated dose). Similarly, the IROC recalculated point dose difference (recalculated dose minus TPS-calculated dose) averaged over the 6 TLD locations was compared against the average of the 6 TLD measured dose differences in the phantom (measured minus TPS) for those same 46 phantom cases. For all relationships, comparisons were done with a linear regression model.

ROC analysis:

The sensitivity and specificity analysis described above considers these two performance criteria separately and does not consider different thresholds (e.g., something other than 90% of pixels passing gamma). Therefore, to assess classification performance across a range of thresholds, our third analysis was to create receiver operator characteristic (ROC) curves. The area under the ROC curve (AUC) was computed for the IROC recalculation results based on all 337 recalculated phantom results. This was done separately for the failing phantom results as well as for the poor phantom results. Following this, a direct comparison was made of the AUC for the recalculation versus the institutional IMRT QA.

As with the regression analysis, because we could not compare between cohorts, this analysis had to be separately done for those phantoms that underwent institutional IMRT QA using a 3%/3mm gamma criteria, those that underwent a 2%/2mm gamma criteria, and those that underwent a point dose evaluation. Each of these cohorts was compared with the independent recalculation approach for the same phantom plans; the recalculation was conducted in the same manner regardless of how the institutional IMRT QA was conducted. The ROC curve was created by allowing the percent of pixels passing gamma (or point dose agreement) threshold to vary (for institutional QA) and allowing the maximum disagreement over the 6 ROIs corresponding to the TLD locations to vary (for the recalculation). As a final step, these evaluations were done for both the failing phantom results as well as the poorly performing phantom results. ROC analysis was done using the pROC package in R.

The AUC summarizes performance across a range of possible thresholds, but does not specify what that good threshold is. Clinically, to implement any form of QA, it is essential to select an appropriate threshold. This information can be determined from the ROC curve by, for example, selecting the point on the curve that achieves a desired sensitivity. It was felt that an 80% sensitivity was a reasonable and desirable objective for an IMRT QA device to achieve. To this end, based on the ROC curves created, we calculated the threshold required to yield 80% sensitivity (i.e., the percent of pixels passing threshold required for the QA method to “fail” 80% of the unacceptable phantom results).

Results

Of the 337 phantom results in the entire cohort, 18 were failing results and 59 were poor results.

Sensitivity and specificity

Table 1 shows truth tables for Institutional IMRT QA (1a) and the Mobius3D recalculation (1b) for the entire cohort of failing phantom irradiations. Of the 18 failing phantom irradiations, institutional IMRT QA only identified a single case, providing a sensitivity of only 6% and showing that the vast majority of unacceptable plans were incorrectly called passing by the institutional IMRT QA. Of the 319 passing phantom irradiations, institutional IMRT QA correctly identified 313 plans as passing, providing a specificity of 98% and showing that the vast majority of acceptable plans were correctly called passing by the institutional IMRT QA. While high specificity is conceptually good, this situation requires further thought because a tighter criterion is used in IMRT QA than in the phantom (~3% vs. 7%). One would expect many plans that passed the phantom to fail IMRT QA because of the tighter criteria (i.e., those results between 3% and 7%). Such cases of disagreement would manifest as a lowered specificity, and so the specificity of this analysis should likely not be extremely high. The fact that the specificity is so high may indicate that IMRT QA is simply passing all plans regardless of quality, a conclusion supported by the corresponding low sensitivity.

Table 1.

Truth tables for all phantom cases. (a) shows institutional IMRT QA results as compared to the truth (IROC phantom assessment). (b) shows IROC recalculations (using Mobius3D and considering the worst point dose agreement) as compared to the IROC phantom.

		IROC phantom					IROC phantom
		Fail	Pass				Fail	Pass
Inst. QA	Fail	1	6		Mobius3D	Fail	13	101
	Pass	17	313			Pass	5	218
		(a)					(b)

The Mobius3D recalculation correctly identified 13 of the failing phantom irradiations, providing a sensitivity of 72%, which was better than that achieved by clinical measurement-based IMRT QA (highly statistically significant; p<0.001). The specificity was lower at 68% (highly statistically significant; p<0.001); the recalculation correctly identified 218 of 319 acceptable phantom results. The lower specificity of this test could be the result of the recalculation being a poorer test than IMRT QA (which had 98% specificity), or, as described in the previous paragraph, reflect an expected outcome because of the tighter criteria used for the recalculation (4%) as compared to the phantom (7%). Further analysis in subsequent sections helps shed additional light on this topic.

Sensitivity and specificity were similarly calculated for the subset of cases that were evaluated by each of the most common IMRT QA devices used in the community. The results are shown in Table 2 for the failing phantom irradiations and show that the independent recalculation consistently outperformed current measurement-based IMRT QA in terms of sensitivity. Most IMRT QA devices showed a 0% sensitivity to detect unacceptable plans (i.e., the QA device incorrectly said all failing phantom irradiations were acceptable). The Mobius3D recalculation showed routinely good sensitivity, which was 100% for two of the cohorts. These differences were statistically significant for most cases; the differences that were not significant may be due to limited sample size (i.e., small number of true failures). Table 3 shows similar results for the poor phantom results (>5% dose errors). Although the recalculation was generally less sensitive at detecting these smaller errors, it nevertheless outperformed (in terms of sensitivity) all of the clinically implemented measurement-based IMRT QA techniques. Across all tests, the improvement in sensitivity was highly significant, and was significant for the EPID, ArcCheck, and MapCheck devices. While Tables 2 and 3 indicate that the sensitivity is better for the recalculation (i.e., it performs better at flagging unacceptable plans), these tables also indicate that the specificity is poorer for the recalculation (i.e., it more often flags acceptable plans). This tradeoff requires further evaluation which is done in subsequent sections.

Table 2.

Sensitivity and specificity of the Mobius3D recalculation as compared to institutional IMRT QA for failing phantom plans. The independent recalculation was consistently more sensitive to detecting unacceptable plans.

Device	# tests	# failing results	% Sensitivity			% Specificity
			IMRT QA	Mobius3D	Sig.	IMRT QA	Mobius3D	Sig.
All	337	18	6	72	**	98	68	**
EPID	58	7	0	71	*	100	57	**
ArcCheck	93	4	0	100	*	100	70	**
Ion Chamber	44	1	0	100		91	67	*
IC + Array	29	0	N/A	N/A		93	62	*
MapCheck	121	5	20	40		100	67	**

^*significant (0.001 to 0.05);

^**highly significant (< 0.001)

Table 3.

Sensitivity and specificity of the Mobius3D recalculation as compared to institutional IMRT QA for poor phantom results (>5% phantom results). The independent recalculation was consistently more sensitive to detecting unacceptable plans.

Device	# tests	# poor results	% Sensitivity			% Specificity
			IMRT QA	Mobius3D	Sig.	IMRT QA	Mobius3D	Sig.
All	337	59	5	47	**	99	69	**
EPID	58	16	0	56	*	100	57	**
ArcCheck	93	16	0	31	*	100	66	**
Ion Chamber	44	8	25	63		94	72	*
IC + Array	29	6	17	50		96	65	*
MapCheck	121	20	5	45	*	100	69	**

^*significant (0.001 to 0.05);

^**highly significant (< 0.001)

Regression analysis

The QA results (either institutional IMRT QA or Mobius recalculation results) were plotted against the phantom result (Figure 1). The relationship between the QA gamma result and the actual phantom gamma result are shown in panel (a). As these two values should, ideally, be similar, the regression lines should show a slope near unity. For IMRT QA conducted with a 2%/2mm criteria, the slope was only 0.07 and the slope was not significantly different than 0 (p=0.4), indicating no significant relationship between the IMRT QA result and the phantom result. The slope was nearly identical for the institutional IMRT QA conducted with a 3%/3mm criteria, being 0.06. Because of the large number of samples, this slope was moderately significant (p=0.04), although it is numerically very small and the small R² value (0.018) indicates no valuable association between the institutional IMRT QA result and the phantom result. The Mobius3D slope was greater (0.23), and was signficant (p=0.003). Although the slope was not particularly close to 1, it was nevertheless more closely related to the actual phantom result than that found from traditional IMRT QA methods.

Figure 1.

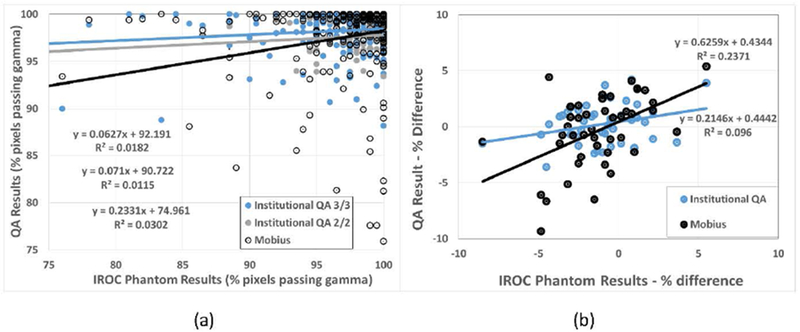
Regression analysis of QA result (Institutional IMRT QA or Mobius3D) versus the actual dose delivered to the phantom. This was for IMRT QA based on point dose measurements (a) and for gamma analysis (b).

Similarly, the results for point doses are shown in panel (b). Again, the slope of the line should be 1, where the QA result is similar to the actual dose deviation in the PTV of the “patient”. The slope of the line for institutional IMRT QA was significantly different from zero (p=0.04), but had a value of only 0.2, indicating a weak relationship between this QA and actual dose to the target. The slope of the line for the Mobius3D recalculation was 0.63 and was highly significant (p<0.001). In short, for both percent of pixels passing gamma and point dose agreement, the independent recalculation more closely represented the actual dose delivered to the phantom than did the institutions’ IMRT QA (p=0.04 based on ANOVA).

ROC analysis

Figure 1 shows the sensitivity and specificity for the independent recalculation considering the entire cohort of 337 phantom results. The two curves are created based on the recalculation’s ability to correctly sort phantom irradiations that failed (failing cohort) and those that were poor performers (poor cohort). Each curve was created by varying the threshold at which the recalculation called a plan “failing” or “poor performing” (i.e., the worst agreement tolerated over the 6 TLD locations in the PTV). For the cohort of phantoms that failed IROC criteria, the AUC was 0.78 (95% CI: 0.69–0.86), indicating that the independent recalculation had reasonable capability at detecting failing plans. For the poor phantom result cohort, the AUC was lower at 0.60 (95% CI: 0.51–0.69), indicating that the recalculation approach was less successful at detecting poor plans.

In the sensitivity and specificity analysis, we somewhat arbitrarily selected a recalculation criterion of 4% (i.e., the dose at each of the 6 TLD locations in the PTV needed to agree within 4% between the planning system and recalculation). Based on the ROC curves of Figure 1, the recalculation criteria that provides an 80% sensitivity for the test (i.e., the recalculation tolerance that would flag 80% of the unacceptable phantom results) can be identified. For the failing cohort, the criterion that achieved an 80% sensitivity was a 3.5% maximum difference at any of the 6 TLD locations in the PTV. That is, if we used a criterion of 3.5% for the maximum deviation (instead of our arbitrary 4%), the recalculation would correctly flag 80% of failing phantom irradiations. A different criterion is necessary to flag poor phantom results. For the poor phantom result cohort, the threshold required to achieve 80% sensitivity was 1.4% (i.e., a much tighter criterion is needed to correctly identify poor phantom irradiation cases than failing cases, which is reasonable because this test is seeking to detect less erroneous results).

There are several Mobius3D metrics that can be used to “flag” a bad result. The worst agreement between measured and calculated doses at any of the 6 TLD locations was used in Figure 1. However, we also evaluated the average disagreement (instead of maximum disagreement) over those 6 locations. The results were nearly identical: The AUC for the failing results was 0.74 for the average disagreement (vs. 0.78 for the maximum disagreement) (95% CI: 0.64–0.84) and the AUC for the poor results was 0.59 (vs. 0.60) (95% CI: 0.50–0.67). Similarly, we also evaluated the percent of pixels passing 3D gamma over the PTV (instead of point differences). This analysis is of interest because it involves the gamma metric instead of point dose differences and therefore captures more of the recalculation result instead of being limited to a comparison at a few points. The AUC results of the 3D gamma evaluation were, again, very similar: the AUC for the failing results was 0.69 for the 3D gamma result (vs. 0.78 for the maximum disagreement) (95% CI: 0.58–0.80) and the AUC for the poor results was 0.59 (vs. 0.60) (95% CI: 0.51–0.67). In short, we did not find any difference in sensitivity or specificity when different metrics were used to evaluate the recalculation analysis.

We next compared ROC curves directly between the IROC recalculation versus institutional IMRT QA for each evaluable cohort of IMRT QA: those based on any array device using a 3%/3mm criteria (n=245, 14 failures, 46 poor results), those based on any array device using a 2%/2mm criteria (n=54, 3 failures, 9 poor results), and those based on point dose evaluation (n=44, 1 failure (not evaluable), 7 poor results). A sample ROC curve for those phantoms evaluated with institutional arrays using a 3%/3mm criterion is shown in Figure 2, where the institutional IMRT QA and independent recalculation are being used to identify failing phantom results.

Figure 2.

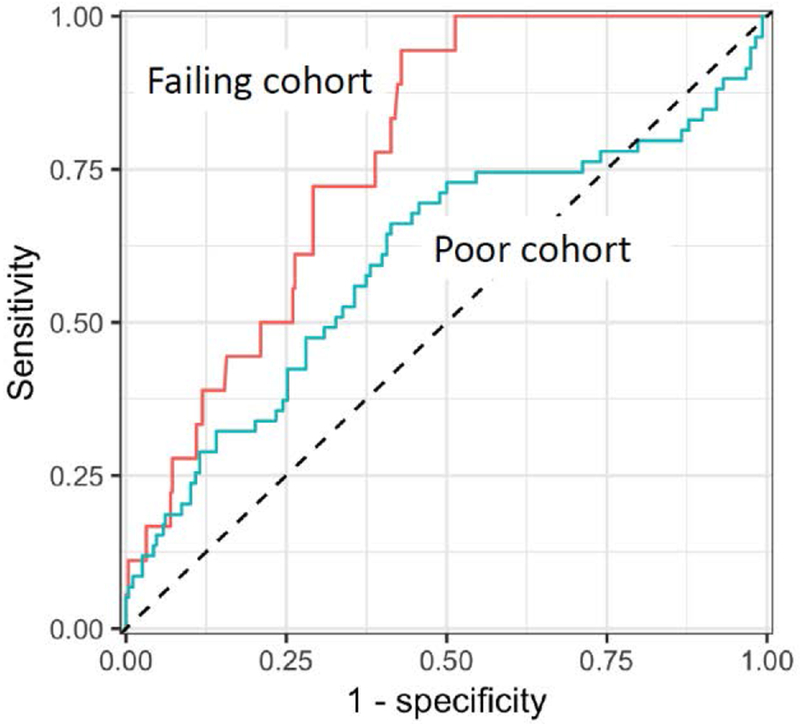
ROC curves for all phantom results as evaluated by the IROC recalculation. The higher line shows the ROC for the failing phantom result cohort (AUC = 0.74) while the lower line shows the ROC for the poor phantom result cohort (AUC = 0.58).

The Mobius3D results in Figure 2 showed an AUC of 0.79 (95% CI: 0.70–0.88), which was significantly better (p=0.01; based on bootstrap test) than the AUC of the institutional IMRT QA approach: AUC 0.60 (95% CI: 0.45–0.76), for which the AUC confidence interval includes 0.5 (i.e., a “random guess”). In addition to the AUC, the criteria required to achieve 80% sensitivity can also be compared for this cohort. For the Mobius3D recalculation, a threshold of 3.6% difference produced a sensitivity of 80%. For the institutional IMRT QA, in order to achieve 80% sensitivity, a threshold of 99.7% of pixels passing gamma was required.

The AUC and 80%-sensitivity comparison for the other IMRT QA cohorts is shown below in Table 4. The AUC for Mobius3D was higher than that for institutional IMRT QA for all but one cohort (2%/2mm criteria evaluating poor phantom results; results not significantly different). While not all recalculation cohorts showed a high AUC, no IMRT QA technique (array or point dose) performed well: all AUCs were low and included 0.5 (“random guess”) in their confidence interval. The threshold required for the system to flag 80% of the unacceptable cases (i.e., to detect failing or poor results) was clinically reasonable (i.e., implementable) for many of the recalculation cohorts. Particularly when trying to detect failing phantom results, thresholds around 4% were observed. For the IMRT QA approaches, based on 3%/3mm or 2%/2mm, the percent of pixels passing gamma threshold needed to be extremely high and clinically unrealistic to implement: between 99.2% and 100% of pixels passing gamma.

Table 4.

AUC results for the independent recalculation with Mobius3D versus institutional IMRT QA for different cohorts: cohorts were defined based on how the institutional IMRT QA was performed (3%/3mm or 2%/2mm gamma analysis with an array, or point dose) and whether the IROC phantom result was a fail or a poor dosimetric result. Table also includes the threshold to achieve 80% sensitivity (i.e., correctly identify 80% of unacceptable plans). Thresholds are maximum % disagreement between recalculation and TPS for Mobius3D. For institutional IMRT QA the threshold is percent of pixels passing gamma or percent difference between point dose and TPS.

Cohort		Mobius3D Recalculation		Inst IMRT QA
IMRT QA criteria	Phantom performance	AUC (95% CI)	Threshold for 80% sensitivity	AUC (95% CI)	Threshold for 80% sensitivity
3%/3mm	Fail	0.79 (0.70-0.88)	3.6%	0.60 (0.45-0.76)	99.7%
2%/2mm	Fail	0.78 (0.60-0.96)	4.1%	0.59 (0.05-1.00)	100%
3%/3mm	Poor	0.59 (0.49-0.69)	1.7%	0.56 (0.46-0.65)	99.8%
2%/2mm	Poor	0.66 (0.43-0.90)	1.4%	0.69 (0.46-0.92)	99.2%
Point dose	Poor	0.80 (0.64-0.97)	2.9%	0.55 (0.29-0.81)	1.4%

Discussion

A wide range of comparisons were made between current measurement-based IMRT QA techniques and a simple recalculation approach. Neither QA approach provided perfect agreement with the results of the phantom evaluation; indeed perfect agreement is unrealistic because measurement-based IMRT QA as well as the recalculation both have different uncertainties and different tolerances than the phantom. While the measurement-based approach and recalculation may offer imperfect specificity (because of the tighter tolerance, as described at the beginning of the results section), the sensitivity of each approach (i.e., the ability to detect an unacceptable plan), is the most clinically relevant component and is a component at which both systems need to perform well. However, considering the sensitivity alone, as well as considering the sensitivity and specificity together, the independent recalculation overwhelmingly outperformed the current measurement-based IMRT QA methods. This outperformance was often dramatic. There are two components to this that require consideration as discussed in the subsequent two paragraphs. First, the performance of traditional IMRT QA methods, and second, the performance of the independent recalculation platform.

The current study reinforces previous findings that traditional IMRT QA methods, as implemented clinically, struggle to detect low quality radiotherapy plans.^3–9 These traditional IMRT QA methods performed consistently poorly in the current study regardless of if they were searching for a large error (failing phantom result) or a moderate error (poor phantom result). The traditional IMRT methods also performed consistently poorly regardless of whether a 3%/3mm criteria was used or a 2%/2mm criteria. This result is particularly dramatic because the dose errors detected by the IROC phantom are most often large, systematic dose errors,² so this is not a failure to detect some trivial issue. While these devices (as a whole) performed poorly across gamma acceptance thresholds, to achieve 80% sensitivity in detecting poor or failing phantom results, a threshold in excess of 99.2% of pixels passing was required (using 3%/3mm or 2%/2mm). Thresholds used in clinical practice are generally much lower than these values, which suppresses sensitivity of these devices and preferentially passes unacceptable plans. This finding, and even the typical necessary value of nearly 100% of pixels passing, is consistent with our previous findings evaluating optimal thresholds.⁶ The results of the current study highlight serious concerns with the current state of IMRT QA: not only does it not detect errors (having very low sensitivity when clinical criteria are used; Table 2 and 3), it appears to be substantially unable to be made viable (very low AUC and clinically unrealistic thresholds required; Table 4). This finding must, of course, be considered in the context of the methods of this study: the performance of the QA devices was based on how they are used clinically, and are weighted by the devices most commonly used. As such, this study did not evaluate or demonstrate that measurement-based approaches cannot work, nor is it implied that measurements are not a critical component of beam model validation and the radiotherapy evaluation process. However, IMRT QA measurement methods, evaluated in aggregate based on current clinical practice, did not produce meaningful results in interpreting the suitability of a treatment plan.

The independent calculation consistently outperformed traditional measurement-based systems but did not have ideal sensitivity or specificity. This recalculation approach would not be expected to have perfect sensitivity because it evaluates only one component of the radiotherapy process: the calculation. Errors in delivery or machine output could not be detected with the process implemented herein, limiting its sensitivity. It is therefore rather surprising that the sensitivity was markedly higher than for measurement-based approaches that should, in theory, be able to detect all of these errors. This recalculation approach would also not be expected to have perfect specificity as the recalculation platform has only a single beam model for each class of accelerator. If a clinic has a linac that isn’t well described by the standard model,^12,13 a stock model will not accurately describe it,¹⁰ which would lead to poor specificity as seen in Tables 2 and 3. The importance of this issue is likely to be substantial when small errors are being sought, and relatively insubstantial when large errors are being sought. The data in this work supports this: when identifying failing phantom results (that show dramatic dose discrepancies) the recalculation had very good sensitivity (Table 2 and 3), and performed well overall with clinically realistic thresholds (Table 4). When identifying modest dose discrepancies (poor phantom results) the generic recalculation tool was less successful, and performed comparably to current measurement-based IMRT QA approaches (Table 4).

Despite these limitations of a simple recalculation, overall, the recalculation outperformed existing standards. A large part of this may be that it focuses on the dose calculation, which has been identified as a weak link in the IMRT process.¹⁰ Another component is likely the independence of the recalculation. The recalculation is based on a completely independent algorithm and completely independent beam data. In contrast, IMRT QA devices and clinical beam models may often be tuned together to generate passing IMRT QA plans. The potential importance of independence is also suggested in our previous study:⁶ in a comparison of measurement-based IMRT QA techniques, a single calibrated ion chamber was the most effective QA approach in identifying unacceptable plans. It is possible that the effectiveness of this approach was at least in part due to the complete independence of the ion chamber calibration and therefore the reported dose.

The issue of independence in the recalculation approach is one of substantial potential interest. On one hand, independence of the recalculation may be a potentially important component of the good sensitivity of this approach. However, it may also be a possible problem in that a standard model won’t do a good job predicting dose from a non-standard linac; in such a case, acceptable plans may often fail a recalculation test. This raises a challenging question about what to do for an institution that does not have a standard linac. The specificity will be improved by tuning the recalculation beam model to better describe the actual linac; however, this reduces independence and invites co-tuning of the QA system and the TPS, which could reduce the sensitivity of the approach.

Conclusions

Compared to current, clinically implemented IMRT QA methods (in aggregate), and using common clinical criteria, Mobius3D-based recalculations were 12 times more sensitive at identifying failing phantom results. In particular, the recalculation was significantly and dramatically superior to IMRT QA using an EPID, an ArcCheck, or a MapCheck device. This improvement persisted when specificity was included as the area under the ROC curve was consistently higher for the recalculation than for traditional IMRT QA. This was particularly true when the recalculation was used to identify failing phantom results (identifying large dose errors). No system (recalculation or measurement-based IMRT QA) was successful at identifying more moderate dose errors (poor phantom results). Overall, this independent recalculation approach was superior to current IMRT QA methods, as broadly implemented across the community, for detecting unacceptable plans.

Figure 3.

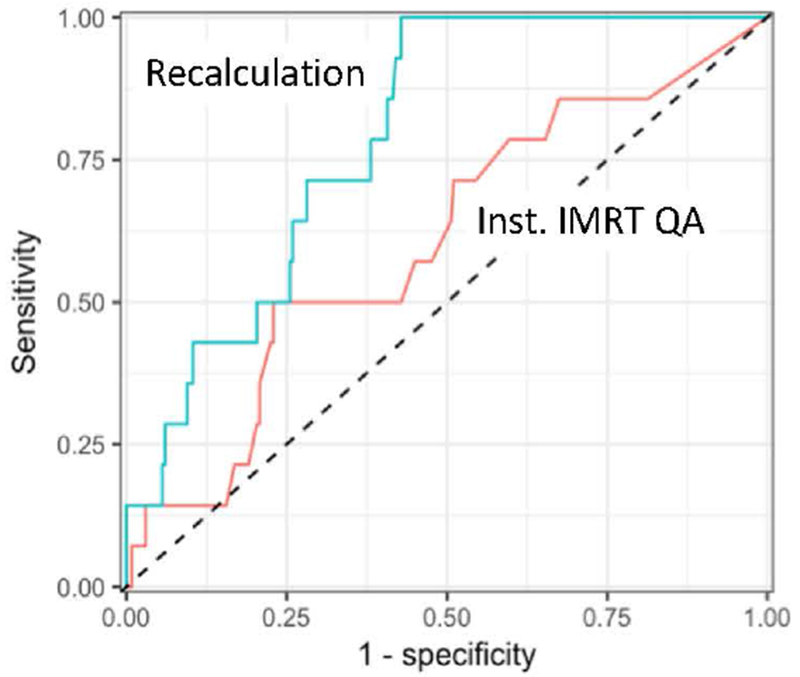
ROC curves for the 245 phantom results evaluated by institutional IMRT QA using an array device and a 3%/3mm criterion. The upper line shows the ROC curve for this cohort evaluated using the IROC recalculation (AUC = 0.79) where the tolerance for dose disagreement in the PTV was varied. The lower line shows the ROC curve for this cohort evaluated using institutional IMRT QA (AUC = 0.60) where the percent of pixels passing gamma was varied. Sensitivity and specificity were relative to identification of phantoms that failed IROC criteria.