Correlated connectivity and the distribution of firing rates in the neocortex

Summary

Two recent experimental observations pose a challenge to many cortical models. First, the activity in the auditory cortex is sparse, and firing rates can be described by a lognormal distribution. Second, the distribution of non-zero synaptic strengths between nearby cortical neurons can also be described by a lognormal distribution. Here we use a simple model of cortical activity to reconcile these observations. The model makes the experimentally testable prediction that synaptic efficacies onto a given cortical neuron are statistically correlated, i.e. it predicts that some neurons receive stronger synapses than other neurons. We propose a simple Hebb-like learning rule which gives rise to such correlations and yields both lognormal firing rates and synaptic efficacies. Our results represent a first step toward reconciling sparse activity and sparse connectivity in cortical networks.

Introduction

The input to any one cortical neuron consists largely of the output from other cortical cells (Benshalom and White, 1986; Douglas et al., 1995; Suarez et al., 1995; Stratford et al., 1996; Lubke et al., 2000). This simple observation, combined with experimental measurements of cortical activity, impose powerful constraint on models of cortical circuits. The activity of any cortical neuron selected at random must be consistent with that of the other neurons in the circuit. Violations of self-consistency pose a challenge for theoretical models of cortical networks.

A classic example of such a violation was the observation (Softky and Koch, 1993) that the irregular Poisson-like firing of cortical neurons is inconsistent with a model in which each neuron received a large number of uncorrelated inputs from other cortical neurons firing irregularly. Many resolutions of this apparent paradox were subsequently proposed (van Vreeswijk and Sompolinsky, 1996; Troyer and Miller, 1997; Shadlen and Newsome, 1998; Salinas and Sejnowski, 2002). One resolution (Stevens and Zador, 1998)—that cortical firing is not uncorrelated, but is instead organized into synchronous volleys, or “bumps”—was recently confirmed experimentally in the auditory cortex (DeWeese and Zador, 2006). Thus a successful model can motivate new experiments.

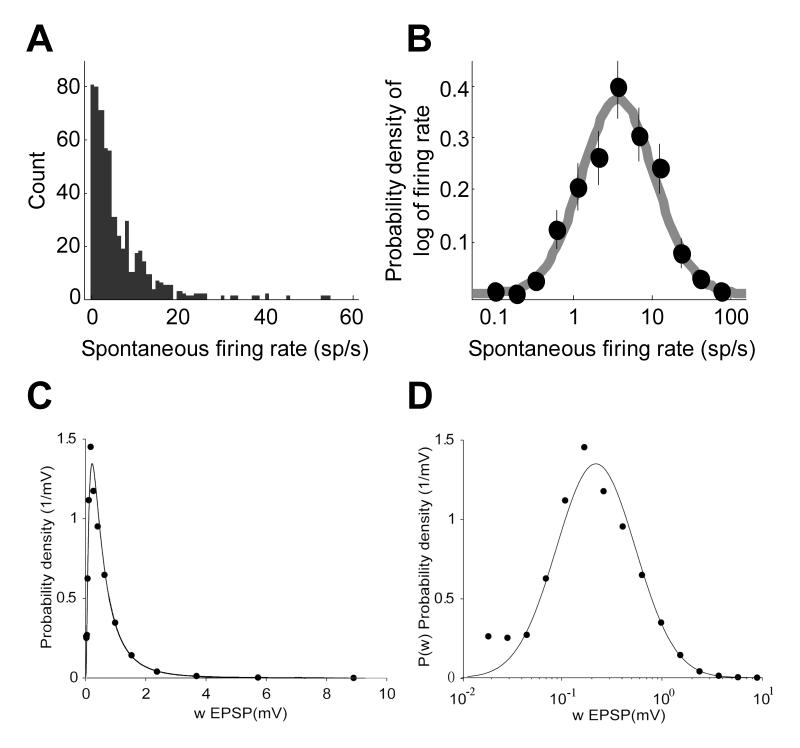
Two recent experimental observations pose a new challenge to many cortical models. First, it has recently been shown (Hromadka et al., 2008) that activity in the primary auditory cortex of awake rodents is sparse. Specifically, the distribution of spontaneous firing rates can be described by a lognormal distribution (Figure 1A and B). Second, the distribution of non-zero synaptic strengths measured between pairs of connected cortical neurons is also well-described by a lognormal distribution (Figure 1C and D; (Song et al., 2005)). As shown below, the simplest randomly connected model circuit that incorporates a lognormal distribution of synaptic weights predicts that firing rates measured across the population will have a Gaussian rather than a lognormal distribution. The observed lognormal distribution of firing rates therefore imposes additional constraints on cortical circuits.

Figure 1.

Lognormal distributions in cerebral cortex.

(A, B) Distribution of spontaneous firing rates in auditory cortex of unanesthetized rats follows a lognormal distribution (Hromadka et al., 2008). Measurements with the cell-attached method show that spontaneous firing rates in cortex vary within several orders of magnitude. The distribution is fit well by a lognormal distribution with some cells displaying firing rate above 30 Hz and an average firing rate of about 3 Hz (black arrow). (C, D) The distribution of synaptic weights for intracortical connections (Song et al., 2005). To assess this distribution, pairs of neurons in the network were chosen randomly and the strength of the connections between them is measured using electrophysiological methods (Song et al., 2005). Most connections between pairs are of zero strength: the sparseness of cortical network is about 20% even if the neuronal cell bodies are close to each other so that the cells have a potential to be connected (Stepanyants et al., 2002; Thomson and Lamy, 2007). This implies that in about 80% of such pairs there is no direct synaptic connection. The distribution of non-zero synaptic efficacies is close to lognormal (Song et al., 2005), at least, for the connectivity between neurons in layer V of rat visual cortex. This implies that the logarithm of the synaptic strength has a normal (Gaussian) distribution.

In this paper we address two questions. First, how can the observed lognormal distribution of firing rates be reconciled with the lognormal distribution of synaptic efficacies? We find that reconciling lognormal firing rates and synaptic efficacies implies that inputs onto a given cortical neuron must be statistically correlated—an experimentally testable prediction. Second, how might the distributions emerge in development? We propose a simple Hebb-like learning rule which gives rise to both lognormal firing rates and synaptic efficacies.

Methods

Generation of lognormal matrices

Weight matrices in Figures 2–4 were constructed using the MATLAB random number generator. Figure 2 displays a purely white-noise matrix with no correlations between elements. To generate the lognormal distribution of the elements of this matrix we first generated a matrix $\widehat{N}$ whose elements are distributed normally, with zero mean and a unit standard deviation. The white-noise weight matrix $\widehat{W}$ was then obtained by evaluating exponential of the individual elements of $\widehat{N}$, i.e. W_ij = exp(N_ij). Elements of the weight matrix obtained with this method have a lognormal distribution since their logarithms (N_ij) are distributed normally. To obtain the column-matrix (Figure 3A) we used the following property of the lognormal distribution: The product of two lognormally distributed numbers is also lognormally distributed. The column matrix can therefore be obtained by multiplying the columns of a white-noise lognormal matrix A_ij, which is generated using the method described above, by a set of lognormal numbers v_j, i.e.

$$W_{ij}=A_{ij}{v}_j.$$ (1)

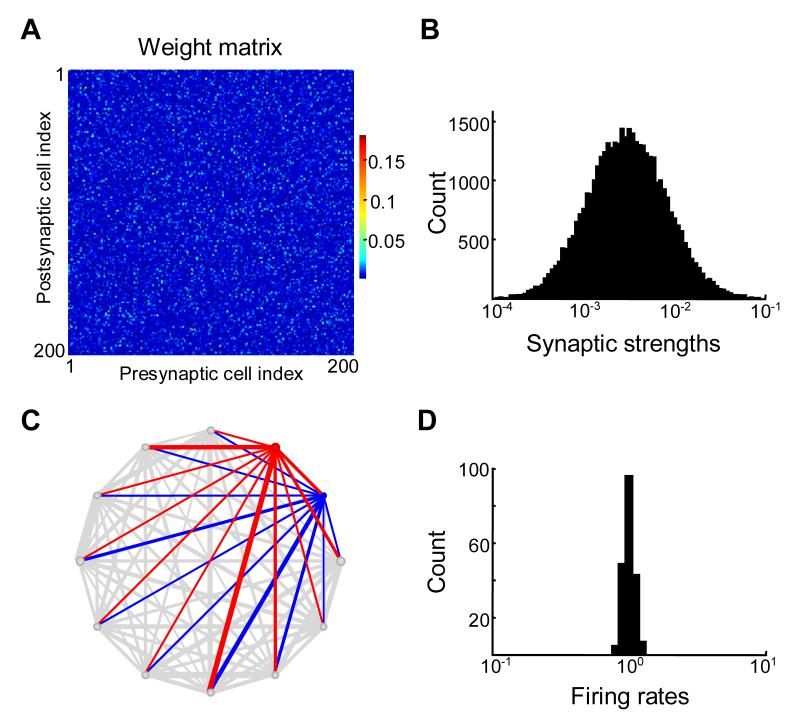
Figure 2.

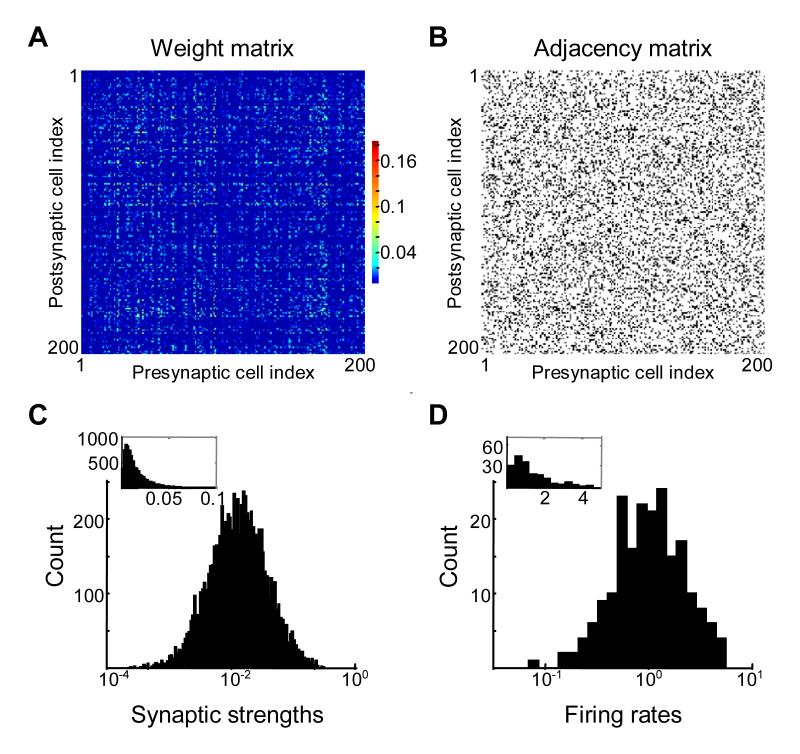
Randomly connected “white noise” network connectivity does not yield lognormal distribution of spontaneous firing rates.

(A) Synaptic connectivity matrix for 200 neurons. Because synaptic strengths are uncorrelated, the weight matrix looks like a “white-noise” matrix.

(B) Distribution of synaptic strengths is lognormal. The matrix is rescaled to yield a unit principal eigenvalue.

(C) Synaptic weights and firing rates of 12 randomly chosen neurons tended to be similar. Every circle corresponds to a single neuron, with diameter proportional to the neuron’s spontaneous firing rate. Thickness of connecting lines is proportional to strengths (synaptic weights) of incoming connections for each neuron. Red and blue circles and lines show spontaneous firing rates and incoming connection strengths for two neurons with maximum and minimum firing rates from the sample shown. Because incoming synaptic weights are similar on average the spontaneous firing rates (circle diameters) tend to be similar.

(D) Spontaneous firing rates given by the components of principal eigenvector of matrix shown in (A). The distribution of spontaneous firing rates in not lognormal, contrary to experimental findings (see Figure 1A and B). The spontaneous firing rates are approximately the same for all neurons in the network.

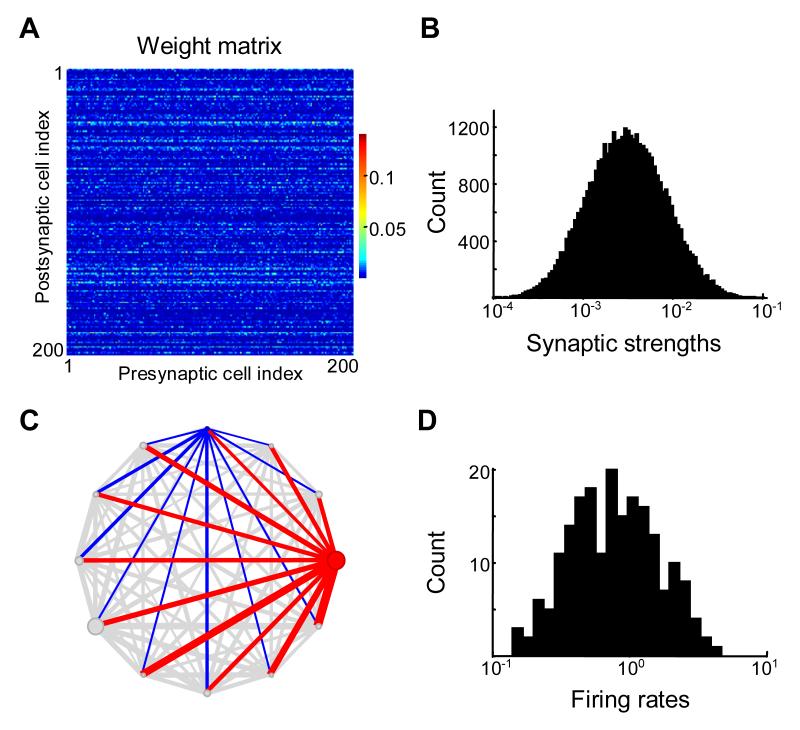
Figure 4.

Correlations among synaptic weights on the same dendrite (input correlations) lead to lognormal distribution of spontaneous firing rates.

(A) Synaptic connectivity matrix for 200 neurons. Note the horizontal “stripes” showing input correlations.

(B) Distribution of synaptic weights is set up to be lognormal.

(C) Inputs into two cells, red and blue are shown by the thickness of lines in this representation of the network. Because synaptic strengths are correlated for the same postsynaptic cell, the inputs into cells marked by blue and red are systematically different, leading to large differences in the firing rates. For the randomly chosen subset containing 12 neurons shown in this example the spontaneous firing rates (circle diameter) vary widely due to large variance in the strength of incoming connections (line widths).

(D) Distribution of spontaneous firing rates is lognormal and has a large variance for row-matrix.

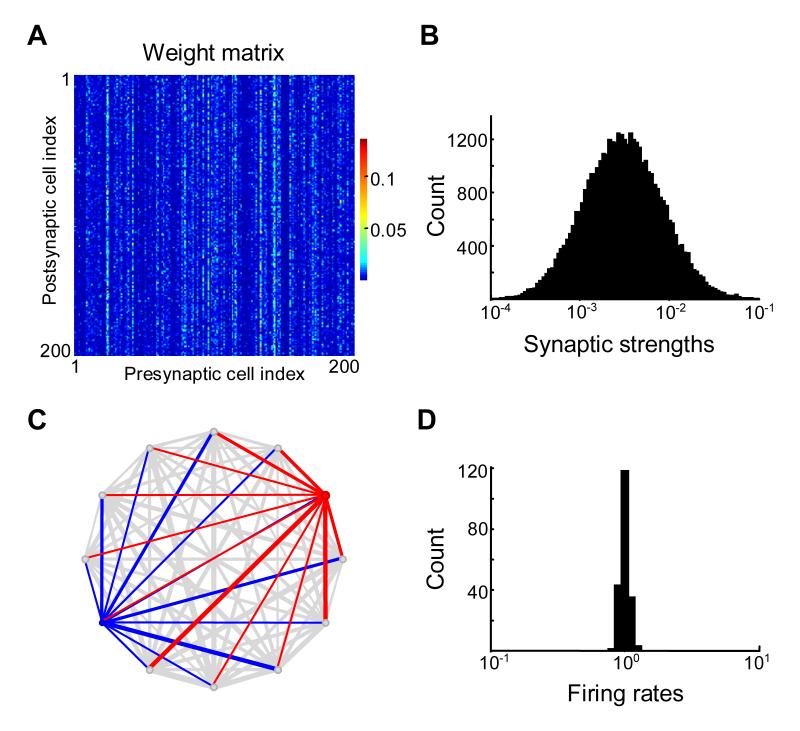
Figure 3.

Correlated synaptic weights on the same axon (output correlations) do not lead to lognormal distribution of spontaneous firing rates.

(A) Synaptic weight matrix for 200 neurons contains vertical “stripes” indicating correlations between synapses made by the same presynaptic cell (the same axon).

(B) Distribution of synaptic weights is lognormal.

(C) Firing rates and synaptic weights tended to be similar for different neurons in the network, as illustrated on an example of 12 randomly chosen neurons. Red and blue circles show neurons with maximum and minimum firing rates (out of the sample shown), with their corresponding incoming connections.

(D) Column-matrix fails to yield broader distribution of spontaneous firing rates than the “white noise” matrix (Figure 2).

Both logarithm of A_ij and logarithm of v_j had zero mean and a unit standard deviation. Similarly, the row-matrix in Figure 4A was obtained by multiplying each row of the white-noise matrix A_ij with the set of numbers v_i:

$$W_{ij}=v_i{A}_{ij}$$ (2)

As in equation (1) both logarithm of A_ij and logarithm of v_j were normally distributed with zero mean and unit standard deviation.

Lognormal firing rates for row-matrices

Here we explain why the elements of the principal eigenvector of row-matrices have a broad lognormal distribution (Figure 4D). Consider the eigenvalue problem for the row-matrix represented by equation (10). It is described by

$$\sum _{j=1}^N{v}_i{A}_{ij}{f}_j=f_i$$ (3)

Equation (3) can be rewritten in the following way

$$\sum _{j=1}^N{A}_{ij}{v}_j\frac{f_j}{v_j}=\frac{f_i}{v_i}$$ (4)

Thus the vector y_i = f_i / v_i is the eigenvector of the column-matrix A_ij v_j [cf. equation (1)]. As such, it is a normally distributed quantity with a low coefficient of variation (CV) as shown in Figure 3.

$$y_i\approx 1$$ (5)

This approximate equality becomes more precise as the size of the weight matrix goes to infinity. Therefore we conclude that

$$f_i\approx v_i.$$ (6)

Because A_ij and v_j are lognormal, both W_ij = v_iA_ij and its eigenvector f_i ≈ v_i are also lognormal.

Non-linear learning rule

Here we show that the non-linear Hebbian learning rule given by equation (11) can yield row-matrix as described by equation (2) in the state of equilibrium. In equilibrium ${\stackrel{.}{W}}_{ij}=0$ and equation (11) yields

$$W_{ij}={\left(\frac{{\epsilon }_1}{{\epsilon }_2}\right)}^{\frac{1}{1-\beta }}{f}_i^{\frac{\alpha }{1-\beta }}{f}_j^{\frac{\gamma }{1-\beta }}{C}_{ij}$$ (7)

Here C_ij is the adjacency matrix (Figure 5B) whose elements are equal to either 0 or 1 depending on whether there is a synapse from neuron number j to neuron i. Note that in this notation the adjacency matrix is transposed compared to the convention used in the graph theory. The firing rates of the neurons f_i in the stationary equilibrium state are themselves components of the principal eigenvector of W_ij as required by equation (10). After substituting equation (7) into equation (10) simple algebraic transformations lead to

$$f_i\sim {\left(\sum _j{C}_{ij}{f}_j^{\frac{\gamma }{1-\beta }}\right)}^{\frac{1-\beta }{1-\alpha -\beta }}\sim (1+{\xi }_i{)}^{\frac{1-\beta }{1-\alpha -\beta }}$$ (8)

Figure 5.

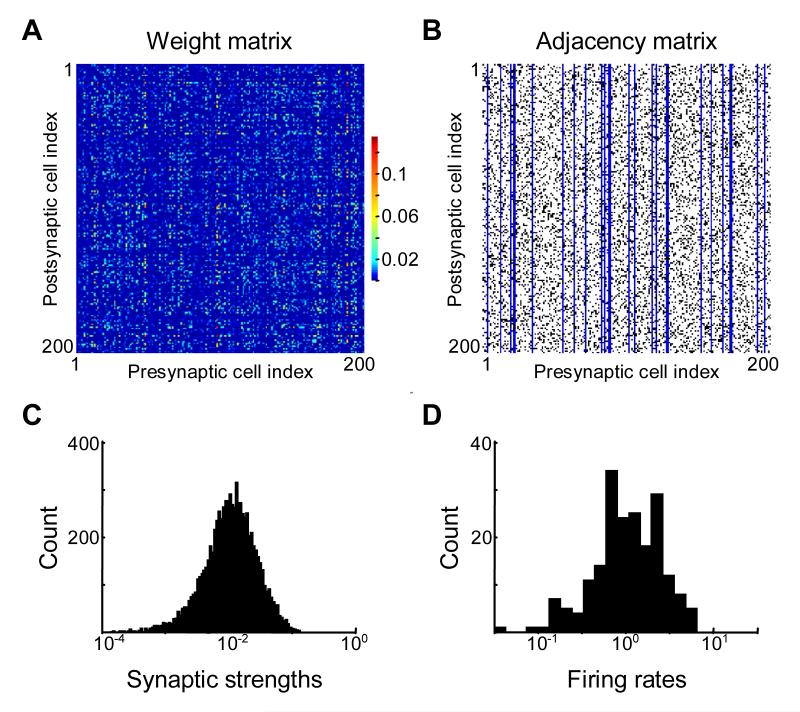
Multiplicative Hebbian learning rule leads to wide network connectivity and firing rate distributions.

(A) Synaptic connectivity matrix for 200 neurons resulting from 1000 iterations of multiplicative Hebbian learning rule. This matrix displays “plaid” structure (horizontal and vertical “stripes”) indicating both input and output correlations. This feature is similar to both column- and row-matrices introduced in previous sections.

(B) The adjacency matrix for the weight matrix shows the connections that are present (non-zero, black) or missing (equal to zero, white). Adjacency matrix defined here is transposed compared to the standard definition in graph theory. The adjacency matrix is 20% sparse and is not symmetric, i.e. synaptic connections formed a directed graph. (C), (D) Distributions of synaptic weights resulting from the non-linear Hebbian learning rule (C) and spontaneous firing rates (D) were approximately lognormal, i.e. appeared as normally distributed on logarithmic axis.

Because the elements of the adjacency matrix are uncorrelated in our model the sum in equation (8) has Gaussian distribution with small coefficient of variation vanishing in the limit of large network. Therefore the variable ξ_i describing relative deviation of this sum from the mean ($\stackrel{‒}{{\xi }_i}=0$) for neuron i is approximately normal with variance much smaller than one. Taking the logarithm of equation (8) and taking advantage of the smallness of variance of ξ_i we obtain

$$\ln f_i\approx \frac{1-\beta }{1-\alpha -\beta }{\xi }_i.$$ (9)

Because ξ_i is normal, f_i is lognormal (Figure 5B). In the limit α+β→1 the variance of the lognormal distribution of f_i diverges according to equation (9). Thus even if ξ_i has small variance, firing rates may be broadly distributed with the standard deviation of its logarithm reaching unity as in Figures 5 and 7. The non-zero elements of the weight matrix are also lognormally distributed, because, according to equation (7) weight matrix is a product of powers of lognormal numbers f_i. These conclusions are discussed in more detail in the Supplementary Material 1.

Figure 7.

The results of non-linear multiplicative learning rule when inhibitory neurons are present in the network.

(A) The absolute values of the weight matrix display the same ‘plaid’ correlations as in the network with excitatory neurons only (Figure 5A).

(B) The adjacency matrix contains inhibitory connections. The presence of non-zero connection is shown by black points (20% sparseness). Positions of the inhibitory neurons in the weight matrix are indicated by the vertical blue lines (15%).

(C) The distribution of absolute values of synaptic strengths resulting from non-linear Hebbian learning rule is close to lognormal with small asymmetry.

(D) The spontaneous firing rates are widely distributed with the distribution that is approximately lognormal.

Details of computer simulations

To generate Figures 5-7 we modeled the dynamics described by equation (11). Temporal derivatives were approximated by discrete differences ${\stackrel{.}{W}}_{ij}\approx \Delta W_{ij}∕\Delta t$ with time step Δt = 1, as described in more detail in Supplementary Material 1. The simulation included 1000 iterative steps. We verified that the distributions of firing rates and weights saturated and stayed approximately constant at the end of the simulation run. For every time step the distribution of spontaneous firing rates was calculated from equation (10) taking the elements of the principal eigenvector of matrix W_ij. Since the eigenvector is defined up to a constant factor, the vector of firing rates was normalized to yield zero average logarithm of its elements. This normalization was performed on each step and was intended to mimic the homeostatic control of the average firing rate in the network. A multiplicative noise of 5% was added to the vector of firing rates on each iteration step. The parameters used were α = β = 0.4, γ = 0.45, ε₁ = 8.2·10^-3, ε₂ = 0.1 in Figures 5 and 6 , and α = β = 0.36, γ = 0.53, ε₁ = 6.9·10^-3, ε₂ = 0.1, in Figure 7. Parameters α, β, and γ were adjusted to yield approximately unit standard deviations of the logarithms of non-zero synaptic weights and firing rates. As α+β→1 the variance of the logarithm of synaptic weights increases [equation (9)]. Because in the case of inhibitory neurons (Figure 7) the adjacency matrix had negative elements and had therefore larger variance than in the case of no inhibition (Figures 5 and 6), parameters α and β had to be decreased slightly in Figure 7 compared to Figures 5 and 6 as described above. Parameters ε₁ and ε₂ provide the overall normalization of the weight matrix. These parameters could be regulated by a slow homeostatic process controlling the overall scale of the synaptic strengths. Their values listed above have been chosen to yield approximately unit principal eigenvalue of the weight matrix (cf. Supplementary Material 1, Section 3).

Figure 6.

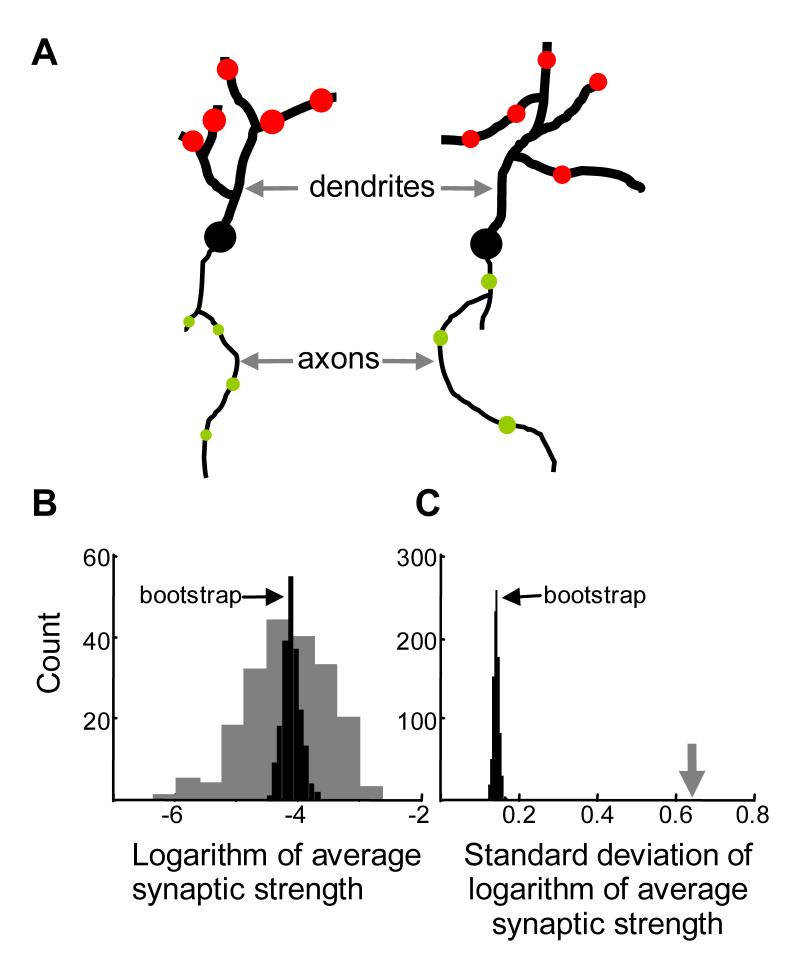
Experimental predictions of this theory.

(A) The presence of row connectivity (Figure 4–5), sufficient for generation of dual lognormal distributions, implies correlations between synaptic strengths on each dendrite (the diameter of the red circle). In addition, if the non-linear Hebbian mechanism is involved in generation of these correlations, the synapses on the same axon are expected to be correlated (plaid-connectivity, Figure 5).

(B) To reveal these correlations, the logarithm of average synaptic strengths (LASS) was calculated for each dendrite. The distribution of these averages for individual dendrites (rows) from Figure 5 is shown by gray bars. The standard deviation of this distribution is about 0.64 in natural logarithm units. The black histogram shows LASS distribution after the synapses were “scrambled” randomly, with their identification with particular dendrites removed. This bootstrapping procedure (Hogg et al., 2005) builds a white-noise matrix with the same distribution of synaptic weights, but much narrower distribution of bootstrapped LASS.

(C) Distribution of standard deviations (distribution widths) of LASS for many iterations of bootstrap (black bars). The widths were significantly lower than the width of the original LASS distribution (0.64, gray arrow). This feature is indicative of input correlations.

Before iterations started random adjacency matrices were generated with 20% sparseness (Figures 5B and 7B). These matrices contained 80% of zeros and 20% of elements that were either +1 or -1 depending on whether the connection was excitatory or inhibitory. In Figure 5 only excitatory connections were present. In Figure 7 the adjacency matrix contained 15% of ‘inhibitory’ columns representing axons of inhibitory neurons. In these columns all of the non-zero matrix elements of the adjacency matrix were equal to -1. The weight matrices were initialized to the absolute value of the adjacency matrix divided by the principal eigenvalue. All simulations were performed in MATLAB (Mathworks, Natick, MA).

Results

Recurrent model of spontaneous cortical activity

To model the spontaneous activity of the i^th neuron in the cortex, we assume that its firing rate f_i is given by a weighted sum of the firing rates f_j of all the other neurons in the network:

$$f_i=\sum _{j=1}^N{W}_{ij}{f}_j.$$ (10)

Here W_ij is the strength of the synapse connecting neuron j to neuron i. This expression is valid if the external inputs, such as thalamocortical projections, are weak (for example, in the absence of sensory inputs, when the spontaneous activity is usually measured), or when recurrent connections are strong enough to provide significant amplification of the thalamocortical inputs (Douglas et al., 1995; Suarez et al., 1995; Stratford et al., 1996; Lubke et al., 2000). Throughout this study we will use a linear model for the network dynamics, both because it is the simplest possible approach that captures the essence of the problem and because cortical neurons often display threshold-linear input to firing rate dependences over substantial range of firing rates (Stevens and Zador, 1998; Higgs et al., 2006; Cardin et al., 2008).

Equation (10) defines the consistency constraint between the spontaneous firing rates f_j and the connection strengths W_ij. mentioned in the introduction. Indeed, given the weight matrix, not all values of spontaneous firing rates can satisfy this equation. Conversely, not any distribution of individual synaptic strengths (elements of matrix W_ij) is consistent with the particular distribution of spontaneous activities (elements of f_j). It can be recognized that equation (10) defines an eigenvector problem, a standard problem in linear algebra (Strang, 2003). Specifically, the set of spontaneous firing rates represented by vector $\stackrel{\mathrm{r}}{f}$ is the principal eigenvector (i.e. the eigenvector with the largest associated eigenvalue) of the connectivity matrix $\widehat{W}$ (Rajan and Abbott, 2006). The eigenvalues and eigenvectors of a matrix can be determined numerically using a computer package such as MATLAB.

Before proceeding, we note an additional property of our model. In order for the principal eigenvector to be stable, the principal eigenvalue must be unity. If the principal eigenvector is greater than one then the firing rates grow without bound to infinity, whereas if the principal eigenvalue is less than one the firing rates decay to zero. Mathematically, it is straightforward to renormalize the principal eigenvalue by considering a new matrix formed by dividing all the elements of the original matrix by its principal eigenvalue. Biologically such a normalization may be accomplished by global mechanisms controlling the overall scale of synaptic strengths, such as the homeostatic control (Davis, 2006), short-term synaptic plasticity, or synaptic scaling (Abbott and Nelson, 2000). Our model is applicable if any of the above mechanisms is involved.

Recognizing that equation (10) defines an eigenvector problem allows us to recast the first neurobiological problem posed in the introduction as a mathematical problem. We began by asking whether it was possible to reconcile the observed lognormal distribution of firing rates (Figure 1A) with the observed lognormal distribution of synaptic efficacies (Figure 1B). Mathematically, the experimentally observed distribution of spontaneous firing rates corresponds to the distribution of the elements f_i of the vector of spontaneous firing rates $\overrightarrow{f}$, and the experimentally observed distribution of synaptic efficacies corresponds to the distribution of non-zero elements W_ij of the synaptic connectivity matrix $\widehat{W}$ . Thus the mathematical problem is: Under what conditions does a matrix $\widehat{W}$ whose non-zero elements W_ij obey a lognormal distribution has a principal eigenvector $\overrightarrow{f}$ whose elements f_i also obey a lognormal distribution?

In the next sections we first consider synaptic matrices with non-negative elements. Such synaptic matrices describe networks containing only excitatory neurons, with positive connection strengths corresponding to synaptic efficacies between excitatory cells and zeros corresponding to no synaptic connection. The properties of the principal eigenvalues and eigenvectors of such matrices are described by the Perron-Frobenius theorem (Varga, 2000). This theorem ensures that the principal eigenvalue of the synaptic matrix is a positive real number, that there is only one solution for the principal eigenvalue and eigenvector, and that the elements of the eigenvector representing in our case spontaneous firing rates of individual neurons are all positive. These properties are valid for the so-called irreducible matrices which describe networks in which activity can travel between any two nodes (Varga, 2000). Because we will consider either fully connected or sparse networks with connectivity above the percolation threshold (Stauffer and Aharony, 1992; Henrichsen, 2000), our matrices are irreducible. Later we will include inhibitory neurons by making some of the matrix elements negative. Although the conclusions of the Perron-Frobenius theorem do not apply directly to these networks, we have found experimentally that they are still valid, perhaps because the fraction of inhibitory neurons was kept small in our model (see below).

Randomly connected lognormal networks do not yield lognormal firing

We first examined the spontaneous rates produced by a “white-noise” matrix in which there were no correlations between elements (Figure 2A). The values of synaptic strengths in this matrix have been generated using random number generator to have a lognormal distribution (Figure 2B) similarly to the experimental observations (Figure 1A) (Song et al., 2005). The standard deviation of the natural logarithm of non-zero connectivity strengths was set to one, consistent with experimental observations. The distribution of the spontaneous firing rates obtained by solving the eigenvector problem for such matrices is displayed in Figure 2D. The spontaneous firing rates had similar values for all cells in the network, with a coefficient of variation of about 5%. It is clear that this distribution is quite different from the experimentally observed one (Figure 1), in which the rates varied over at least one order of magnitude.

To understand why the differences in the spontaneous firing rates between cells were not large with white noise connectivity, consider two cells in a network illustrated by red and blue circles in Figure 2C. Width of connecting edges is proportional to connection strength, and the circle diameters are proportional to firing rates. All inputs into these two cells came from the same distribution with the same mean as specified by the white-noise matrix. Since each cell received a large number of such inputs, the differences in the total inputs between these two cells were small, due to the central limit theorem. The total inputs were approximately equal to the mean input values multiplied by the number of inputs. Therefore one should expect that the firing rates of the cells were similar, as observed in our computer simulations.

The connectivity matrix with no correlations between synaptic strengths therefore is inconsistent with experimental observations of dual lognormal distributions for both connectivity and spontaneous activity. We next explored the possibility that introducing correlations between connections would yield the two lognormal distributions.

Presynaptic correlations do not yield lognormal firing

We first considered the effect of correlations between the strengths of synapses made by a particular neuron. These synapses are arranged columnwise in the connectivity matrix shown in Figure 3A (column-matrix). To create these correlations we generated a white-noise lognormal matrix and then multiplied each column by a random number chosen from another lognormal distribution. The elements of resulting column-matrix were also lognormally distributed (Figure 3B) as products of two lognormally distributed random numbers (see Methods).

As shown in Figure 3, presynaptic correlations did not resolve the experimental paradox between the distributions of spontaneous firing rates and synaptic strengths. Although the connectivity matrix was lognormal (Figure 3B), the spontaneous activity had a distribution with low variance (Figure 3D). A different type of correlations was needed to explain high variances in both distributions.

The reason why the column-matrix failed to produce dual lognormal distributions is essentially the same as in the case of white-noise matrix. Each neuron in the network received connections taken from the distributions with the same mean. With large number of inputs, the differences between total inputs into individual cells become small due to the central limit theorem, with the total input being approximately equal to the average of the distribution multiplied by the number of inputs. Thus two cells in Figure 3C received a large number of inputs with the same mean. There were correlations between inputs from the same presynaptic cell but these correlations only increased the similarity in firing rates between two postsynaptic cells. For this reason the variance of the distribution of the spontaneous firing rates was even smaller in the case of column-matrix (Figure 3D) than in the case of white-noise connectivity (Figure 2D). This is also shown in the Supplementary Materials 1 (Section 5). A different type of correlation is therefore needed to resolve the apparent paradox defined by the experimental observations.

Postsynaptic correlations yield lognormal firing

We finally tried network connectivity in which synapses onto the same postsynaptic neuron were positively correlated. Because such synapses impinged upon the same postsynaptic cell, their synaptic weights were arranged row-wise in the connectivity matrix (“row-matrix,” Figure 4A). The row-matrix was obtained by multiplying rows of white-noise matrix by the same number taken from the lognormal distribution (see Methods). This approach was similar to the generation of the column-matrix. It ensured that the non-zero synaptic strengths had a lognormal distribution (Figure 4B).

The resulting distribution of spontaneous firing rates was broad (Figure 4D). It had all the properties of the lognormal distribution, such as the symmetric Gaussian histogram of the logarithms of the firing rates (Figure 4D). One can also prove that the distribution of spontaneous rates as defined by our model is lognormal for the substantially large row-correlated connectivity matrix (see Methods). We conclude that the row-matrix is sufficient to generate the lognormal distribution of spontaneous firing rates.

The reason why the row-matrix yielded a broad distribution of firing rates is illustrated in Figure 4C. Two different neurons (blue and red) received a large number of connections in this case. But these connections were multiplied by two different factors, each depending on the postsynaptic cell (compare the different widths of lines entering the blue and red cells in Figure 4C). Therefore the average values of the strengths of the synapses onto this neuron were systematically different. Since both non-zero matrix elements and the spontaneous firing rates in this case followed a lognormal distribution, the positive correlations between strengths of synapses on the same dendrite could underlie the dual lognormal distributions observed experimentally.

Hebbian learning rule may yield lognormal firing rates and synaptic weights

In the previous section we showed that certain correlations in the synaptic matrix could yield lognormal distribution for spontaneous firing rates given lognormal synaptic strengths. A sufficient condition for this to occur is that the strengths of the synapses onto a given postsynaptic neuron must be correlated. To prove this statement we used networks that were produced by a random number generator (see Methods). The spontaneous activity then was the product of predetermined network connectivity. The natural question is whether the required correlations in connectivity can emerge naturally in the network through one of the known mechanisms of learning, such as Hebbian plasticity. Since Hebbian mechanisms strengthen synapses that have correlated activity, the synaptic connections become products of spontaneous rates too. Thus, network activity and connectivity are involved into mutually-dependent iterative process of modification. It is therefore not immediately clear if the required correlations in the network circuitry (row-matrix) can emerge from such an iterative process.

Rules for changing synaptic strength (learning rules) define the dynamics by which synaptic strengths change as a function of neural activity. We use the symbol ${\stackrel{.}{W}}_{ij}$ to describe the rate of change in synaptic strength from cell number j to i. In the spirit of Hebbian mechanisms, we assume that this rate depends on the presynaptic and postsynaptic firing rates, denoted by f_j and f_i respectively. In our model, in contrast to conventional Hebbian mechanism, the rate of change is also determined by the value of synaptic strength W_ij itself, i.e.

$${\stackrel{.}{W}}_{ij}={\epsilon }_1{f}_i^{\alpha }{W}_{ij}^{\beta }{f}_j^{\gamma }-{\epsilon }_2{W}_{ij}$$ (11)

where as above f_i and f_j are firing rates of the post- and presynaptic neurons i and j, respectively, and ε₁, ε₂, α, β, and γ are parameters discussed below. This equation implies that the rate of synaptic modification is a result of two processes: one for synaptic growth (the first term on the right hand side) and another for synaptic decay (the second term). The former process implements Hebbian potentiation, while the latter represents a passive decay. The relative strengths of these processes are determined by the parameters ε₁ and ε₂.

The Hebbian component is proportional to the product of pre- and postsynaptic firing rates and the current value of synaptic strength. Each of these factors is taken with some powers α,β,γ, which are essential parameters of our model. When the sum of exponents α+β exceeds 1 a single weight dominates the weight matrix. The sum α+β of the exponents must be below 1 to prevent the emergence of winner-takes-it-all solutions. The learning rule considered here is therefore essentially non-linear.

When the sum of exponents α+β approaches 1 from below, the distribution of synaptic weights becomes close to lognormal (see Methods for details). In our simulations (Figure 5) we used α+β=0.8, i.e. value close to one.

In addition to a lognormal distribution of synaptic weights, the learning rule also yielded a lognormal distribution of spontaneous firing rates (Figure 5D). When the structure of synaptic matrix was examined visually, it revealed both vertical and horizontal correlations (Figure 5A). The resulting weight matrix therefore combined the features of row- and column-matrices. The lognormal distribution of spontaneous rates arose, as discussed above (Figure 4), from the correlations between inputs into each cell, i.e. from the row-structure of the synaptic connectivity matrix. The correlations between outputs (column-structure) emerged as a byproduct of the learning rule considered here. Because of the combined row-column correlations we call this type of connectivity patterns a “plaid” connectivity.

The proposed learning rule [equation (11)] preserved the adjacency matrix. This implies that if two cells were not connected by a synapse, they do not become connected as a result of the learning rule. Similarly the synapses are not eliminated by the learning rule. Therefore, although the synaptic connectivity matrix appears to be symmetric with respect to its diagonal (Figure 5A) the connectivity is not fully symmetric as shown by the distribution of non-zero elements in Figure 5B. Our Hebbian plasticity therefore preserves the sparseness of connectivity. In the Methods section we analyze the properties of plaid connectivity in greater detail. We conclude that multiplicative non-linear learning rule can produce correlations sufficient to yield dual lognormal distributions.

Experimental predictions

Here we outline mathematical methods for detecting experimentally the correlations predicted by our model. Our basic findings are summarized in Figure 6A. For the lognormal distributions of both synaptic strengths and firing rates (dual lognormal distributions) it is sufficient that the synapses of the same dendrite are correlated. This implies that the average strengths estimated for individual dendrites are broadly distributed. Thus, the synapses of the right dendrite in Figure 6A are stronger on average than the synapses on the left dendrite. This feature is indicative of the row-matrix correlations shown in Figures 6 and 5. In addition, if the Hebbian learning mechanism proposed here is implemented, the axons of the same cells should display a similar property. This implies that the average synaptic strength of each axon is broadly distributed. We suggest that these signatures of our theory could be detected experimentally.

Modern imaging techniques permit measuring synaptic strengths of substantial number of synapses localized on individual cells (Kopec et al., 2006; Micheva and Smith, 2007). These methods allow monitoring the postsynaptic indicators of connection strength in a substantial fraction of synapses belonging to individual cells. Therefore these methods could allow detecting the row-matrix connectivity (Figure 4) using the statistical procedure described below. The same statistical procedure could be applied to presynaptic measures of synaptic strengths to reveal plaid connectivity (Figure 5).

We illustrate our method on the example of postsynaptic indicators. Assume that the synaptic strengths are available for several dendrites in a volume of cortical tissue. First, for each cell we calculate the logarithm of average synaptic strength (LASS). We obtain a set of LASS characteristics matching in size the number of cells available. Second, we observe that the distribution of LASS is wider than expected for the white-noise matrix (Figure 6B, gray histogram). A useful measure of the width of distribution is its standard deviation. For the dataset produced by the Hebbian learning rule used in the previous section the width of distribution of LASS is about 0.64 natural logarithm units (gray arrow in Figure 6C). Third, we use the bootstrap procedure (Hogg et al., 2005) to assess the probability that the same width of distribution can be produced by the white-noise matrix, i.e. with no correlations present. In the spirit of bootstrap we generate the white noise matrix from the data by randomly moving the synapses from dendrite to dendrite, either with or without repetitions. The random repositioning of the synapses preserves the distribution of synaptic strengths but destroys the correlations, if they are present. The distribution of LASS is evaluated for each random repositioning of synapses of dendrites (iteration of bootstrap). One such distribution is shown for the data in the previous section in Figure 6B (black). It is clearly narrower than in the original dataset. By repeating the repositioning of synapses several times one can calculate the fraction of cases in which the width of the LASS distribution in the original dataset is smaller than the width in the reshuffled dataset. Smallness of this fraction implies that the postsynaptic connectivity is substantially different from the white-noise matrix. For the connectivity obtained by the Hebbian mechanism in the previous section, after 10⁶ iterations of bootstrap we observed none with the width of distribution of LASS larger than in the original non-permuted dataset (Figure 6C). We conclude that it is highly unlikely that the data in Figure 5 describe the white-noise matrix (p-value < 10^-6).

A similar bootstrap analysis could be applied to axons, if sets of synaptic strengths are measured for several axons in the same volume. A small p-value in this case would indicate the presence of column-matrix. The latter may be a consequence of the non-linear Hebbian mechanism proposed in the previous section.

Inhibitory neurons

Cortical networks consist of a mixture of excitatory and inhibitory neurons. We therefore tested the effects of inhibitory neurons on our conclusions. We added a small (15%) fraction of inhibitory elements to our network. Introduction of inhibitory elements was accomplished through the use of an adjacency matrix. The adjacency matrix in this case described both the presence of a connection between neurons and the connection sign. Thus an excitatory synapse from neuron j to neuron i was denoted by an entry in the adjacency matrix C_ij equal to one; inhibitory/missing synapses were described by entries equal to -1 or 0 respectively (Figure 7B). The presence of inhibitory neurons was reflected by the vertical column structure in the adjacency matrix (Figure 7B). Each blue column in Figure 7B represented the axon of a single inhibitory neuron. We then assumed that the learning rules described by equation (11) applied to the absolute values of synaptic strengths of both inhibitory and excitatory synapses with W_ij defining the absolute value of synaptic strength, and the adjacency matrix C_ij its sign. The resulting synaptic strengths and spontaneous firing rate distributions are presented in Figure 7C, D after a stationary state was reached as a result of the learning rule (11). Both distributions were close to lognormal. In addition the synaptic matrix W_ij displayed the characteristic plaid structure obtained previously for purely excitatory networks (Figure 5). We conclude that the presence of inhibitory neurons does not change our previous conclusions qualitatively.

Discussion

We have presented a simple model of cortical activity to reconcile the experimental observation that both spontaneous firing rates and synaptic efficacies in the cortex can be described by a lognormal distribution. We formulate this problem mathematically in terms of the distribution of eigenvalues of the network connectivity matrix. We show that the two observations can be reconciled if the connectivity matrix has a special structure; this structure implies that some neurons receive many more strong connections than other neurons. Finally, we propose a simple Hebb-like learning rule which gives rise to both lognormal firing rates and synaptic efficacies.

Lognormal distributions in the brain

The Gaussian distribution has fundamental significance in statistics. Many statistical tests such as the t-test require that the variable is question have a Gaussian distribution (Hogg et al., 2005). This distribution is characterized by bell-like shape and an overall symmetry with respect to its peak. The lognormal distribution on the other hand is asymmetric and has much heavier “tail”, i.e. decays much slower for large values of the variable than the normal distribution. A surprising number of variables in neuroscience and beyond are described by the lognormal distribution. For example the interspike intervals (Beyer et al., 1975), the psychophysical thresholds for detection of odorants (Devos and Laffort, 1990), the cellular thresholds for detection of visual motion (Britten et al., 1992), the length of words in the English language (Herdan, 1958), and the number of words in a sentence (Williams, 1940) are all united by the fact that their distributions are close to lognormal.

The present results were motivated by the observation that both spontaneous firing rates and synaptic strengths in cortical networks are distributed approximately lognormally. The lognormality of connection strengths was revealed in the course of systematic simultaneous recordings of connected neurons in cortical slices (Song et al., 2005). The lognormality of spontaneous firing rates was observed by monitoring single unit activity in auditory cortex of awake head-fixed rats (Hromadka et al., 2008) using cell attached method. In the traditional extracellular methods cell isolation itself depends upon the spontaneous firing rate: cells with low firing rate are less likely to be detected. During cell attached recordings, cell isolation is independent on the spontaneous or evoked firing rate. Thus cell attached recordings with glass micropipettes permit a relatively unbiased sampling of neurons.

Lognormal distributions of spontaneous firing rates and synaptic strengths were observed experimentally in different cortical areas and in different preparations. The former distribution was observed in primary auditory cortex in vivo (Hromadka et al., 2008), while the latter was revealed from in vitro recording in slices obtained from rat visual cortex (Song et al., 2005). We base our study on the assumption of uniformity of properties of cortical networks, i.e. that functional form of the distributions of spontaneous firing rates and synaptic weights can be generalized from area to area.

Novel Hebbian plasticity mechanism

Spontaneous neuronal activity levels and synaptic strengths are related to each other through mechanisms of synaptic plasticity and network dynamics. We therefore asked the question of how could lognormal distributions of these quantities emerge spontaneously in the recurrent network? The mechanism that induces changes in synaptic connectivity is thought to conform to the general idea of Hebbian rule. The specifics of the quantitative implementation of the Hebbian plasticity mechanism are not clear, especially in the cortical networks. Here we propose that a non-linear multiplicative Hebbian mechanism could yield lognormal distribution of connection strengths and spontaneous rates. We propose that the presence of this mechanism can be inferred implicitly from another correlation in the synaptic connectivity matrix. We argued above that the lognormal distribution in spontaneous rates may be produced by correlations between strengths of synapses on the same dendrite. By contrast, the signature of the non-linear Hebbian plasticity rule is the presence of correlations between synaptic strengths on the same axon. Exactly the same test as we proposed to detect dendritic correlations could be applied to axonal data. The presence of both axonal and dendritic correlations leads to the so-called “plaid” connectivity, named so because both vertical and horizontal correlations are present in the synaptic matrix (Figure 5 and 6).

The biological origin of the nonlinear multiplicative plasticity rules is unclear. On one hand, the power-law dependences suggested by our theory [equation (11)] are sublinear in the network parameters, which corresponds to saturation. On the other hand the rate of modification of the synaptic strengths is proportional to the current value of the strength in some power, which is less than one. This result is consistent with the cluster models of synaptic efficacy, in which the uptake of synaptic receptor channels occurs along a perimeter of the cluster of existing receptors (Shouval, 2005). In this case the exponent of synaptic growth is expected to be close to 1/2 [β =1 / 2, see equation (11)].

Other possibilities

We have proposed that the lognormal distribution of firing rates emerges from differences in the inputs to neurons. An alternative hypothesis is that the lognormal distribution emerges from differences in the spike generating mechanism that lead to a large variance in neuronal input-output relationship. However, the coefficient of variation of the spontaneous firing rates observed experimentally was almost 120% (Figure 1A). There are no data to suggest that differences in the spike generation mechanism would be of sufficient magnitude to account for such a variance (Higgs et al., 2006).

Another, more intriguing possibility is that the lognormal distribution arises from the modulation of the overall level of synaptic noise (Chance et al., 2002) which can sometimes change neuronal gain by a factor of three or more (Higgs et al., 2006). However, in vivo intracellular recordings reveal that the synaptic input driving spikes in auditory cortex is organized into highly synchronous volleys, or “bumps” (DeWeese and Zador, 2006), so that the neuronal gain in this area is not determined by synaptic noise. Thus modulation of synaptic noise is unlikely to be responsible for the observed lognormal distribution of firing in auditory cortex.

Broad distributions of synaptic strengths, resembling the one studied here, was observed in hippocampal cultured cells (Murthy et al., 1997). Because these cells were grown in isolation on small “islands” of substrate, they predominantly formed synapses with themselves i.e. autapses. Because in our study we considered the network mechanism, finding wide distribution of autaptic strengths in isolated neurons should require a different explanation. However, a mathematically similar Hebbian mechanism, applied to individual branches of a non-isopotential neuron (Brown et al., 1992; Perlmutter, 1995; Losonczy et al., 2008), may provide an alternative explanation.

Conclusions

The lognormal distribution is widespread in economics, linguistics, and biological systems (Bouchaud and Mezard, 2000; Limpert et al., 2001; Souma, 2002). Many of the lognormal variables are produced by networks of interacting elements. The general principles that lead to the recurrence of lognormal distributions are not clearly understood. Here we suggest that lognormal distributions of both activities and network weights in neocortex could result from specific correlations between connection strengths. We also propose a mechanism based on Hebbian learning rules that can yield these correlations. Finally, we propose a statistical procedure that could reveal both network correlations and Hebb-based mechanisms in experimental data.