Fig. 2.

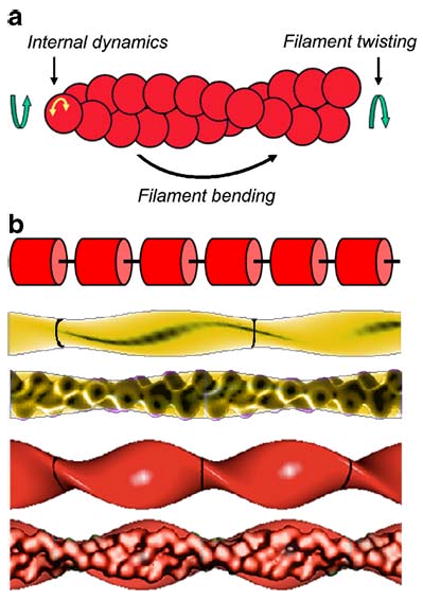
Conformational dynamics of actin filaments. a Schematic representation of actin filament thermal motions. Figure is adapted from Prochniewicz et al. (2005). b Models used to analyze material properties of filaments. Top to bottom Schematic of a linear array of cylindrical subunits connected by a flexible elastic linker that is used when modeling filament torsional dynamics. An actin filament (yellow) modeled with an elliptical cross-section of a 2.7-nm minor radius, a 4.5-nm major radius and 37-nm crossover lengths, and a cofilactin filament (red) modeled with an elliptical cross-section of a 2.7-nm minor radius, a 6.7-nm major radius and 27-nm crossover lengths. These geometric models were used to calculate the second moment of inertia (I) and apparent elastic modulus (E) from the filament flexural rigidity. An actin filament modeled as a homogenous isotropic elliptical cylinder has a second moment of inertia (I) of 120 nm⁴. Cofilin binding increases the filament radius and has a value of 240 nm⁴ for I. Models are presented with and without overlays of the corresponding reconstructions based on cryoelectron microscopy (McGough et al. 1997). Parts of the figure are adapted from McCullough et al. (2008)