Abstract
To determine whether plasma lactate can be a significant fuel for human brain energy metabolism infusions of [3-13C]lactate and 1H-13C polarization transfer spectroscopy were used to detect the entry and utilization of lactate. During the 2-hour infusion study, 13C incorporation in the amino acid pools of glutamate and glutamine were measured with a 5 minutes time-resolution. With a plasma concentration ([Lac]P) being in the 0.8–2.8 mmol/L range, the tissue lactate concentration ([Lac]B) was assessed as well as the fractional contribution of lactate to brain energy metabolism (CMRlac). From the measured relationship between unidirectional lactate influx (Vin) and plasma and brain lactate concentrations lactate transport constants were calculated using a reversible Michaelis-Menten model. The results show (i) that in the physiological range plasma lactate unidirectional transport (Vin) and concentration in tissue increases close to linearly with the lactate concentration in plasma, (ii) the maximum potential contribution of plasma lactate to brain metabolism is 10% under basal plasma lactate conditions of ~ 1.0 mmol/L and as much as 60% at supra-physiological plasma lactate concentrations when the transporters are saturated, (iii) the half-saturation constant KT is 5.1±2.7 mmol/L and VMAX is 0.40±0.13 μmol/g/min (68% confidence interval), (iv) the majority of plasma lactate is metabolized in neurons similar to glucose.
Keywords: Human, Brain metabolism, Lactate transport, NMR, In vivo 13C Spectroscopy, reversible Michaelis-Menten
INTRODUCTION
In the traditional view of brain energy metabolism, glucose is the predominant energy substrate (Siesjö, 1978) with lactate returned to the circulation as a metabolic by-product of glycolytic (non-oxidative) excess. Under normal resting conditions, lactate is present in the blood at a concentration of ~0.5–1.0 mmol/L and the brain is a small net exporter of lactate (Siesjö, 1978; Sokoloff, 1989; Harada et al., 1992). However, lactate can cross the blood-brain-barrier through monocarboxylate transporters (MCTs) (Oldendorf, 1973, Simpson et al., 2007) and recent studies have provided evidence that lactate can become a significant fuel source when elevated in the blood (Smith et al., 2003; van Hall et al., 2009). Plasma lactate may also be an important fuel source for the brain during hypoglycemia. Maran and coworkers (Maran et al., 1994) reported that infusion of lactate allows maintenance of normal human brain evoked potentials during hypoglycemia. Recently, we reported that acetate transport from blood to brain, which involves monocarboxylate transporters, was greater in subjects with well controlled type-1 diabetes. We hypothesized that plasma lactate could potentially be an important net fuel source during insulin-induced hypoglycemia (Mason et al., 2006). Furthermore, there is evidence from in vitro and in vivo experiments that lactate may be required energetically to support synaptic function (for review see Pellerin et al., 2005), potentially via shuttling of glycolytically-derived carbons from astroglia to neurons (Magistretti et al., 1999; Pellerin et al., 2005) for oxidation.
Combined with 13C-labeled substrates and appropriate metabolic modeling, nuclear magnetic resonance spectroscopy (MRS) allows for non-invasive measurement of metabolic fluxes in human brain based on the dynamic detection of 13C incorporation into the large cerebral pools of glutamate and glutamine (Rothman et al., 1992; Gruetter et al., 1994, 2001; Lebon et al., 2002; Lin et al., 2003). Human cerebral metabolism of 13C-labeled glucose, acetate (Bluml et al., 2002; Lebon et al., 2002), and β-hydroxybutyrate (Pan et al., 2000; 2001; 2002) have been investigated with 13C or 1H-{13C} MRS (for reviews see Shen and Rothman, 2002; Hyder et al., 2006). In this report, we describe the first use of [3-13C]labeled lactate with in vivo 13C MRS to directly assess transport kinetics and metabolism of plasma lactate in the human cerebral occipital cortex, as well as estimate the relative contributions of plasma lactate to neuronal and glial metabolism.
MATERIALS AND METHODS
Subjects
Seven young healthy volunteers (four females and three males; aged 24±1; mean ± SD, BMI 24±1 kg/m2) were recruited for this study. Written consent was obtained from each subject after the purpose and potential risks were explained. The protocol was approved by the Yale University Human Investigation Committee. They were all healthy, lean, nonsmokers and taking no medications. All subjects underwent a complete medical history and physical examination along with blood tests to verify normal hemoglobin, hematocrit, electrolytes, aspartate aminotransferase, alanine aminotransferase, blood urea nitrogen, creatinine, cholesterol and triglycerides. Nine NMR studies were performed according to two different infusion protocols (A and B) designed to rapidly raise and maintain plasma lactate 13C fractional enrichment (fe[LacC3]P) to either (A) 33% while maintaining plasma lactate concentration ([Lac]P) at close to physiological levels (~1.5 mmol/L) or (B) 50% while maintaining plasma lactate at twice the physiological levels (~2.5 mmol/L).
After an overnight fast, an intravenous catheter was placed in an antecubital vein in each arm for the infusion and for blood sampling. After placement of catheters, the subject was positioned within the magnet, and acquisition optimization was performed. After acquisition of the baseline spectrum, [3- 13C]lactate was infused (350 mmol/L sodium salt 99% 13C enriched, Cambridge Isotopes, Cambridge, MA, USA) at either (A) a priming dose of 150 μmol/kg given over 5min followed by a continuous infusion of 10 μmol/kg/min for approximately 120 min, or (B) a priming dose of 300 μmol/kg given over 5min followed by a continuous infusion of 20 μmol/kg/min for approximately 120min. Each volunteer underwent either protocol A or B, and two subjects underwent both, leading to a total of 12 experiments of which 9 were used for kinetic analysis.
MRS acquisition
MRS data were acquired on a 4.0 T whole-body magnet interfaced to a Bruker AVANCE spectrometer (Bruker Instruments, Billerica, MA, USA). Subjects were placed supine in the magnet, with the head immobilized with foam, lying on top of a radiofrequency probe consisting of one 13C circular coil (8.5 cm diameter) and two 1H quadrature coils for acquisition and decoupling. After tuning, acquisition of scout images, shimming with the FASTERMAP procedure (Shen et al., 1997) and calibration of decoupling power, 13C spectra were acquired before and during the [3-13C]lactate infusion using a localized adiabatic 13C-{1H} refocused INEPT sequence optimized for glutamate and glutamine in the C4 position using 3D-ISIS combined with outer volume saturation (OVS) for localization on the 1H magnetization (Shen et al., 1999) (128 transients, TR=2.5s, 5.3min time-resolution). The spectroscopic volume was located in the occipital-parietal lobe, with its size adapted to each volunteer and was on average 106 ± 1.6 mL (mean ± SD, n=9).
Data processing
MRI Segmentation
The tissue composition of each voxel was determined from T1-based image segmentation maps according to a previously described protocol (Hetherington et al., 1996; Mason and Rothman, 2002). Briefly, sets of B1 maps and inversion-recovery images were acquired and processed to yield quantitative T1 maps, which were converted to segmented images of gray matter, white matter and CSF. The gray matter volume was 47 ± 1.8% of tissue content in the voxel (mean ± SD, n=9).
Spectral analysis
All the spectra were analyzed using LCModel 6.1 (Provencher, 1993) (Stephen Provencher Inc., Oakville, ON, Canada) modified to process 13C spectral data as explained by Henry et al. (Henry et al., 2003). The LCModel basis set was generated by simulating spectra for every observable isotopomer with NMRSim 2.8 (Bruker Analytik GmbH, Ettlingen, Germany) using published values of 13C chemical shifts and homonuclear 13C-13C coupling constants (JCC) from Henry et al. (Henry et al., 2003). Resonances quantified included the C3 position of aspartate (AspC3), the C2, C3 and C4 positions of glutamate (GluC2, GluC3, GluC4) and glutamine (GlnC2, GlnC3 GlnC4), the C3 position of N-acetyl aspartate (NAAC3) and the C3 position of lactate (LacC3). The spectra were added three by three in running averages of 16 min in order to increase the SNR before processing. A 3-Hz-gaussian apodization and zero-filling to 8K data points were applied to all the spectra prior to the LCModel analysis. Relative concentrations obtained from LCModel were converted to absolute concentrations by referring to the natural abundance (1.1%) signal of NAAC3 assuming a NAA pool size of 11 μmol/g in the voxel, based on 1H MRS measurements from a similar region (Michaelis et al., 1993; Mangia et al., 2006). Calibration of the basis set to account for differences in polarization transfer efficiency and off-resonance effects were realized using a series of phantom experiments (data not shown). For the very first time points, due to low SNR, systematic over-estimations were apparent, in order to avoid them, for the first 30min, peak heights were determined manually and scaled on the last spectra. Besides, to improve reliability, only the singlet signals were considered for glutamate (GluC4, GluC3 and GluC2) and glutamine (GlnC4, GlnC3 and GlnC2). Based on probabilities of obtaining double and triply labeled isotopomers, correction factors were calculated and applied to account for the contribution of these isotopomers (GluC43, GluC32, GluC234, GlnC43, GlnC32 and GlnC234).
Measurement of Brain Lactate Concentration
The brain lactate concentration was determined from the measured concentration of 13C3 lactate ([LacC3]B) by assuming that the lactate fractional C3 fractional enrichment (fe[LacC3]B) was the same as that of glutamate C4 at steady state (fe[GluC4]), as a consequence of the lactate/pyruvate pool being the immediate precursor for acetyl-coA which is the precursor for the glutamate C4 and C5 carbons (Mason et al., 1995):
| [1] |
Metabolic modeling analysis
13C Time-courses, Modeling and Metabolic Fluxes Determination
Previous labeling experiments have established that cerebral metabolism can be characterized by two distinct metabolic compartments associated to neurons and glial cells (Lebon et al., 2002 and references therein). 13C Labeling time-courses for glutamate and glutamine in the C4, C3 and C2 positions and the C3 position of lactate were fitted according to this two-compartment metabolic model (Sibson et al., 2001; Gruetter et al., 2001; Lebon et al., 2002; Henry et al., 2006) using Matlab (The MathWorks Inc., Natick, MA) and CWave (Mason et al., 2003) with time-courses for plasma lactate and glucose concentrations and 13C fractional enrichments as input functions. Values for the rates of neuronal and glial TCA cycles (respectively noted VTCAn and VTCAg) and the unidirectional rate of lactate uptake (Vin) were estimated using a simulated annealing algorithm. The neuronal/astroglial glutamate/glutamine cycle (Vcycle) was defined as 0.33 of VTCAn according to previous infusion studies in humans (Lebon et al., 2002). The mitochondrial/cytosolic glutamate/α-ketoglutarate exchange rate in neurons and astrocytes (VXn and VXg) were fitted to improve the accuracy of the TCA cycle rates determination (Mason et al., 1992; Gruetter et al., 2001). Pyruvate carboxylase activity (VPC) was considered equal to 0.06 of Vcycle based on the value reported previously by Mason et al. (2007) following infusion of [2-13C]glucose in humans. The concentrations of glutamate and glutamine used for the modeling were assumed to be 9.1 and 4.1 μmol/g, respectively, as reported previously by MRS in a similar volume (Gruetter et al., 1994).
To estimate the early time-course of the brain lactate fractional enrichment a reversible Michaelis-Menten model of lactate transport was used (see below). A KT of 4.4 mmol/L was assumed based on previous characterization of MCT transporters (Bröer et al., 1998; Manning Fox et al., 2000). Iteration was done with the values of VMAX and KT to obtain the least-squares fit of the measured time-courses. In order to assess whether the transport parameters would have a significant impact on the calculated metabolic rates we performed fits of the data using KT values covering the full range compatible with the results (see Results). Due to the small size of the lactate pool relative to the large metabolic flux passing through it (glycolysis and lactate transport) the value of KT had minimal impact on the derived rates since in all cases the brain lactate pool rapidly achieved isotopic steady-state relative to the labeled precursor.
To account for the probable contribution of the circulating 13C-labeled lactate to the overall [3-13C]lactate signal, a vascular fraction of 3 to 5% of the total volume was calculated for each experiment according to the voxel composition leading to the subsequent correction (Leenders et al., 1990). In addition, to take into account any scrambling of label lactate into plasma glucose by the liver, the plasma glucose C1 and C6 labeling time-courses were used as an input function along with the fractional enrichment of plasma C3 lactate.
Modeling of Lactate Transport Kinetics and Calculation of KT and VMAX/KT
To model lactate transport we used a reversible Michaelis-Menten model (see Figure 1). The physical distribution space of lactate was assumed to be similar to glucose at Vd = 0.77 mg/dL (Gjedde and Diemer, 1983; Gruetter et al., 1996). The reversible Michaelis-Menten kinetics have been described in detail (Mahler and Cordes, 1971; Cunningham et al., 1986) and used successfully to study glucose transport kinetics in human brain (Gruetter et al., 1998; de Graaf et al., 2001; Choi et al., 2001). Detailed kinetic modeling and meta-analysis of literature results by Simpson et al. (2007) have supported it as accurately describing brain glucose and monocarboxylic acid transport. At steady state, the reversible Michaelis-Menten model results in the following expressions for the influx (Vin), efflux (Vout), the net consumption of lactate (CMRlac) and the brain lactate level ([Lac]B):
| [2] |
| [3] |
| [4] |
| [5] |
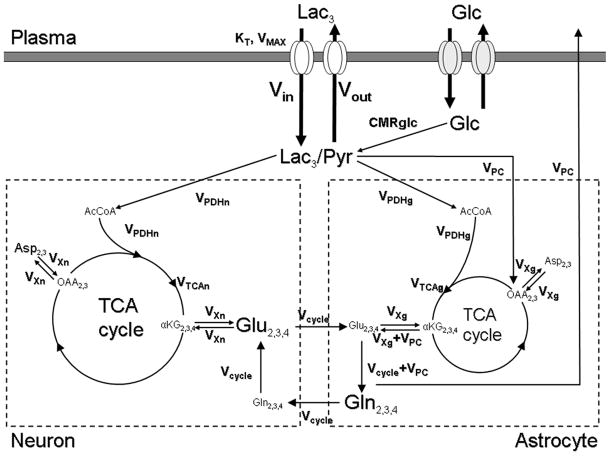
FIG. 1.
Two-compartment model describing the incorporation of label from [3-13C]lactate into the brain glutamate and glutamine pools. Left: neuronal compartment; Right: astroglial compartment. Lac, lactate; Glc, glucose; Pyr, pyruvate; AcCoA, acetyl coenzyme A; OAA, oxaloacetate; αKG, α-ketoglutarate; Glu, glutamate; Gln, glutamine; Asp, aspartate; Vin, influx of lactate; Vout, efflux of lactate; CMRglc, glucose consumption; VPDHn, neuronal flux through the pyruvate dehydrogenase; VPDHg, astroglial flux through the pyruvate dehydrogenase; VTCAn, neuronal TCA cycle rate; VTCAg, astroglial TCA cycle rate; VPC, flux through the pyruvate carboxylase; Vcycle, glutamate/glutamine cycle flux; VXn, mitochondrial/cytosolic glutamate/α-ketoglutarate exchange rate in neurons; VXg, mitochondrial/cytosolic glutamate/α- ketoglutarate exchange rate in astrocytes. In our experiment, 13C-labeled lactate cross the blood brain barrier back and forth through the monocarboxylate transporters (KT, VMAX) and arrives at the C3 of the lactate/pyruvate pool (regrouped as a unique pool because of the very fast exchange between them through the lactate deshydrogenase), where the label enters the TCA cycle via pyruvate carboxylase or pyruvate dehydrogenase reaction. It is ultimately detected at the first turn of the TCA cycle in the C4 position of glutamate and glutamine then, after label scrambling by the TCA activity, on the C2 and C3 positions of glutamate and glutamine.
The last expression predicts that [Lac]B is a linear function of plasma lactate level ([Lac]P) when CMRlac is constant. Equations [2] and [3] can be combined, resulting in:
| [6] |
and
| [7] |
Thus, equation [2] can be rearranged yielding:
| [8] |
From equation [8] it is seen that Vin is highly sensitive to the VMAX/KT ratio and secondarily sensitive to the values VMAX and KT independently.
To estimate VMAX and KT and the corresponding uncertainty, we performed a Monte Carlo analysis based on the relationships of Vin and [Lac]B versus [Lac]P and the best fits of Eq. [5] and [8] to the experimental data, using a least-squares minimization (see Figure 6). For the Monte Carlo analysis, the noise was estimated as Gaussian distributions with standard deviations equal to the difference between the measured values and least-squares fitted values of Vin and [Lac]B. Random Gaussian noise with the same standard deviation was added 100 times to the least-squares fitted values to create 100 noisy simulations of the data. The 100 simulated noisy sets were fitted to generate a list of 100 values of VMAX and KT, which were used to calculate standard deviations of their respective uncertainties (Mason et al., 1992).
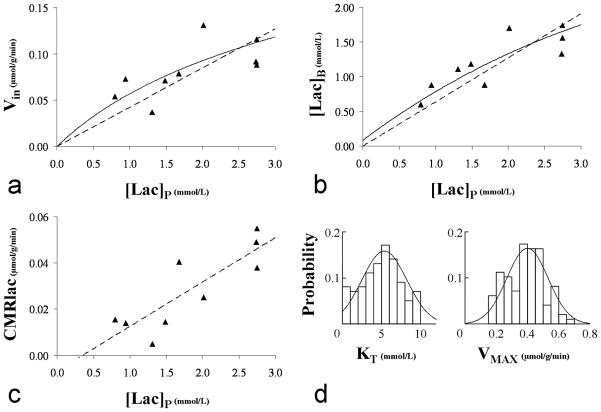
FIG. 6.
A Lactate influx plotted as a function of the plasma lactate concentration. The dashed straight line represents the linear regression which has a slope of 0.042 and a R2 value of 0.58. B. Brain lactate as a function of the plasma lactate concentration. The dashed straight line represents the linear regression which has a slope of 0.63 and a R2 value of 0.75. For both A and B, the solid curve line represents the best fit obtained from a least-square minimization using expressions [5] and [8] given by the reversible Michaelis-Menten model. C. Lactate net consumption plotted as a function of the plasma lactate concentration. The dashed straight line represents the linear regression: CMRlac (in μmol/g/min) = 0.019.[Lac]P-0.007, R2=0.72. D. Overlay of the probability density functions and corresponding histograms for KT and VMAX values derived from the Monte Carlo analysis (see Materials & Methods for details) of the data presented in A and B : KT= 5.1±2.7 mmol/L and VMAX=0.40±0.13 μmol/g/min (mean±SD).
Calculation of Net Lactate Consumption
The net lactate consumption was calculated using the measured values of Vin, [Lac]P, [Lac]B and equation [7]. Note that as shown in the derivation of equation [7] with the reversible Michaelis-Menten model, net consumption within our narrow range of plasma lactate levels can be derived from measurement of intracellular and plasma lactate and Vi,
Insensitivity of the calculation of Vin to Transport Kinetics
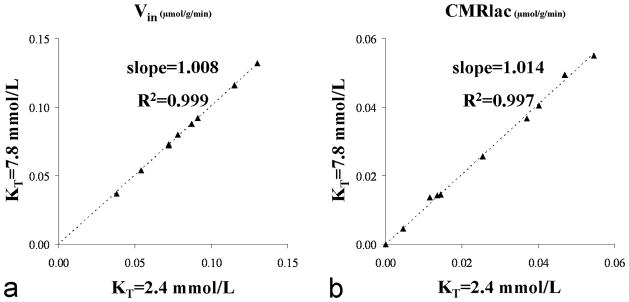
The unidirectional rate of lactate transport Vin was calculated from the 13C labeling time-courses (see above). Because assumed lactate transport parameters were used in the fitting to better fit the beginning of the time-courses when brain lactate fractional enrichment was not at steady state, there is the possibility of circularity in which the assumed transport constants (at the initial iteration of the fits) biases the subsequent values calculated from the Vin plots. To test this possibility, the fits to the data were repeated considering the mean and probability distributions of KT as determined from the Monte Carlo simulations, checking the fits over a range of ± one SD. In the end, over this range an effect of less than 1.4% was observed both on the calculated Vin and CMRlac values (figure 7).
FIG. 7.
A. Lactate influx values and B. Net consumption of lactate obtained from the dynamic modeling of the data assuming KT being either equal to the mean-SD = 2.4 or mean+SD = 7.8 mmol/L (as determined from the Monte Carlo simulations). The impact observed on the estimated Vin and CMRlac values is negligible as illustrated by the slopes (~1.01) and R2 coefficients (>0.99) of the linear regressions.
The reason for the insensitivity of the Vin measurement to lactate transport kinetics (KT, VMAX) can be shown by considering the relative fractional enrichment of plasma and brain lactate at steady state based upon the relative fluxes in and out of the lactate pool as derived from the metabolic model in Figure 1:
| [9] |
By combining the relations [9] and [6], one can derive the relation [10] so that
| [10] |
As shown in equation [10] there is sufficient information at steady state to calculate Vin from knowledge of the relative fractional enrichments and concentrations of plasma and brain lactate at steady state and the rate of the brain TCA cycle without any influence of transport kinetics.
Blood sample processing
During the study, venous blood samples were withdrawn for glucose and lactate assays. Glucose assays were performed using a Beckman Glucometer (Beckman, Fullerton, CA, USA); lactate assays were performed using an YSI 2300 analyzer. Fractional enrichment was determined by gas chromatography-mass spectroscopy. The distribution of 13C label among the six glucose carbon atoms was then determined.
Comparison with studies that used [1-13C]glucose and [2-13C]acetate
Another group of 8 healthy young subjects (three females and five males; aged 26±7; mean ± SD, BMI 23±4 kg/m2) underwent a set of [1- 13C]glucose and [2-13C]acetate infusions. Spectra were obtained from the same occipito-parietal location and the respective data acquisition, infusion protocols and data processing procedure were identical to those described here for the [3-13C]lactate experiments. More detailed descriptions of the infusion protocols and analysis for this group are given elsewhere (Boumezbeur et al., 2010).
RESULTS
Plasma
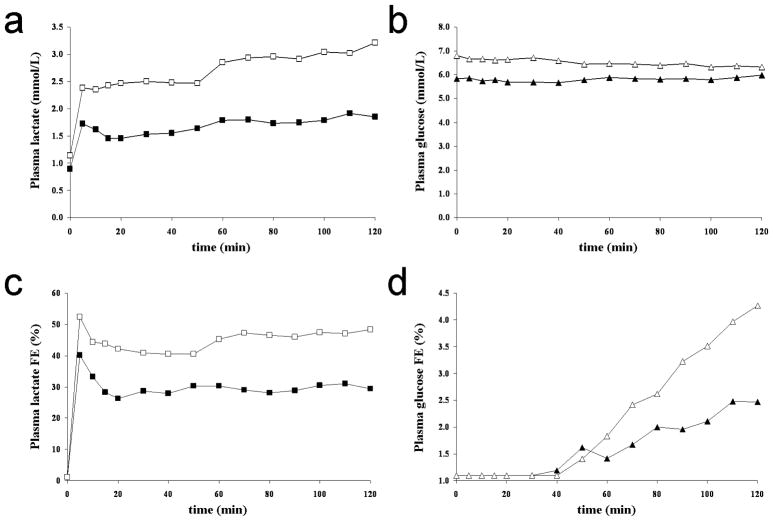
Figures 2A-D show typical plasma lactate ([Lac]P) and glucose ([Glc]P) concentrations and 13C fractional enrichment time-courses for the two different infusion protocols A and B from one volunteer. For each protocol, the targeted [Lac]P and fractional enrichment were attained in the first 5 minutes and their levels remained steady throughout the 2 hour infusions. The range of concentration for plasma lactate achieved by the two infusion protocols (A and B) was 0.8 to 2.8 mmol/L, while the range of steady state fractional enrichment of [3-13C]lactate in plasma achieved was 23.0 to 50.4% with a mean value of 36.2 ± 0.9% (mean ± SD, n=9). It is important to note that circulating [3-13C]lactate is metabolized by the liver and will transfer 13C-label into glucose through gluconeogenesis (Lebon et al., 2002; Rothman et al., 1991; Cohen, 1987). As determined by gas chromatography-mass spectroscopy of blood samples, the incorporation of 13C-label into the C1, C2, C5 and C6 positions of plasma glucose were found to be significant for the C1 and C6 positions with similar fractional enrichments over natural abundance at the end of the infusion: 3.9 ± 0.7% for C1 and 3.5 ± 0.6% for C6 (mean ± SD, n=9). In order to take into account the contribution of 13C-labeled glucose to the measured time-courses, 13C-glucose time-courses have been incorporated to the modeling as an input function.
FIG. 2.
A. Time-courses of plasma lactate concentrations, B. glucose concentration (in mmol/L), C. plasma lactate 13C fractional enrichment (FE) and D. glucose 13C fractional enrichment from the same volunteer for the two different infusion protocols A (black symbols) and B (white symbols). As aimed, plasma lactate level is either (protocol A) maintained close to a physiological level (~1.5 mmol/L) with a 13C FE close to 33% or (protocol B) doubled (~2.5 mmol/L) with a 13C FE close to 50%. Even if the plasma glucose level remains steady at euglycemic values, as the circulating [3-13C]lactate is metabolized by the liver, 13C atoms are progressively incorporated into the plasma glucose through gluconeogenesis.
Brain 13C-labeled metabolite quantification
Figure 3 shows a steady-state spectrum from one of the volunteer, obtained from the last 32 minutes of a 2-hour [3-13C]lactate infusion study as well as its decomposition by LCModel. As described, the multiple positions of glutamate, glutamine and aspartate are well resolved with typical Cramér-Rao lower bounds values (CRLB) at the end of the study being below 5% for GluC4, below 15% for GluC3, GlnC4, GluC2 and AspC3 and below 25% for NAAC3, GlnC3 and GlnC2. However, to improve the detection and quantification of [3-13C]lactate signal (LacC3) at 21ppm, we assumed a rapid establishment of a steady brain lactate concentration and used the sum of all spectra acquired over the 2-hour of infusion. This way, the LacC3 peak was detected and quantified with CRLB between 9 and 30%.
FIG. 3.
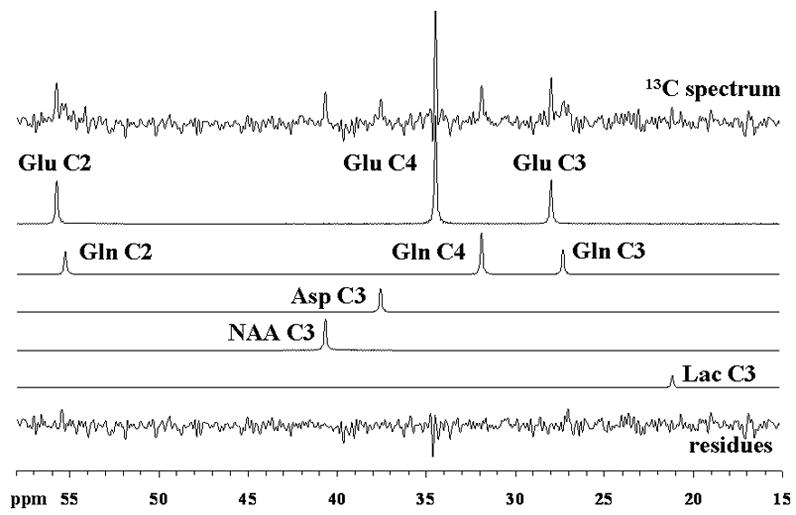
Localized 13C spectrum acquired from the occipito-parietal lobe of a volunteer during the last 32 minutes of a 2-hour [3-13C]lactate infusion study and its decomposition by LCModel. Singlets for GluC4, GluC3, GluC2, GlnC4, GlnC3, GlnC2, AspC3, LacC3, NAAC3 and the residues are displayed. For processing parameters, see Materials & Methods.
Comparison of steady-state labeling from [3-13C]lactate with [2-13C]acetate and [1-13C]glucose
In order to assess whether the oxidation of lactate is primarily glial, or instead is similar to that of glucose we compared the labeling from a 2-hour [3-13C]lactate infusion with labeling from [1-13C]glucose and [2- 13C]acetate. The steady-state spectrum presented in figure 4. A may be compared to that acquired from the same volunteer following [1-13C]glucose (figure 4B) and [2-13C]acetate infusions (figure 4C). The spectra were scaled based on their natural abundance peaks of NAAC3. While the high labeling of GlnC4 resonance for the acetate infusion reflects clearly the compartmentation of acetate oxidization in glia (Hassel et al., 1995; Bachelard, 1998, Lebon et al., 2002), the pattern of labeling for glucose and lactate infusions are very similar except for the minimal 13C-13C sidebands to the glutamate and glutamine resonances. The 13C-13C sidebands which would result from doubly-labeled molecules are not observable due to the low fractional labeling of acetyl-coA following the lactate infusion (see Table 1). To account for these undetected resonances small correction factors (~1.04 for GluC4 and GluC2, ~1.11 for GluC3) were applied. As can be seen in Table 1, the [4-13C]glutamine/[4-13C]glutamate (fe[GlnC4]/fe[GluC4]) labeling ratio extracted from our set of [3-13C]lactate infusions (0.78 ± 0.04, n=9) does not differ significantly (p=0.14, Kolmogorov-Smirnov two-sample test) from the one obtained with [1-13C]glucose infusions (0.87 ± 0.04, n=7). In contrast, there is a large difference in labeling with the results from the [2- 13C]acetate infusions (p=1, Kolmogorov-Smirnov two-sample test) which exhibit a much higher fe[GlnC4]/fe[GluC4] ratio (2.90 ± 0.22, n=7).
FIG. 4.
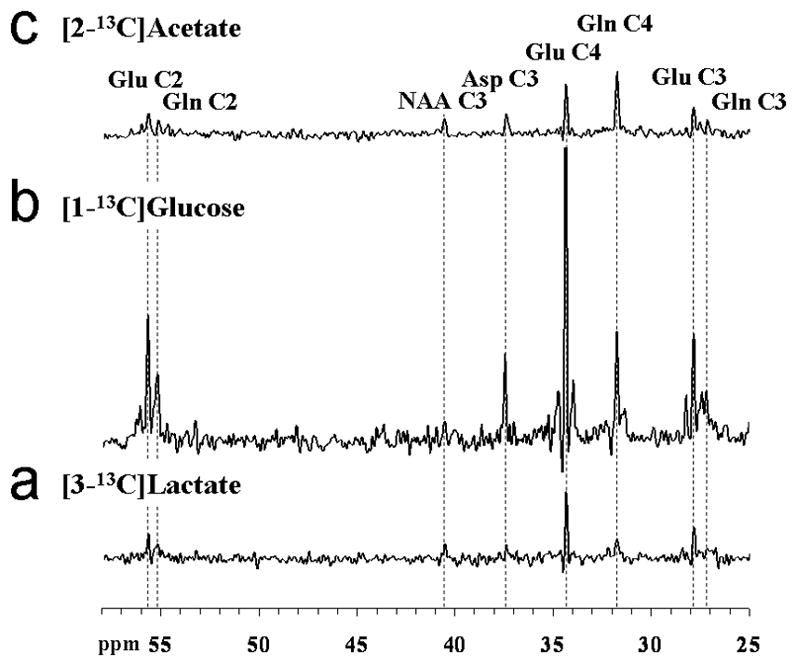
Localized 13C spectra acquired from the occipito-parietal lobe of the same volunteer either during the last 25 minutes of a 2-hour [3-13C]lactate infusion study ([Lac]P ~ 1.5 mmol/L and 13C FE ~ 29%) (A, bottom), during the last 15 minutes of a 2-hour [1-13C]glucose (B, middle), or the last 25 minutes of a 2-hour [2-13C]acetate infusion (C, top), scaled to exhibit the differences in 13C fractional enrichment reached for glutamate and glutamine. For processing parameters, see Materials & Methods.
Table 1.
13C Fractional enrichment of glutamate and glutamine in position C4 and C3 for [2-13C]acetate, [1-13C]glucose and [3-13C]lactate infusions in the human occipito-parietal lobe at the end of 2-hour of infusions. At the bottom line, the [4-13C]glutamine/[4-13C]glutamate labeling ratio is calculated for each individual experiment and averaged. Fractional enrichment values are in %, means ± SD, n=9 for lactate group while n=7 for the glucose and acetate group. The natural abundance (1.1%) is not subtracted. Kolmogorov-Smirnov two-sample tests for difference between lactate and other groups: * p=0.14 with glucose while ** p=1 with acetate.
| [3-13C]Lactate | [1-13C]Glucose | [2-13C]Acetate | |
|---|---|---|---|
| fe[GluC4] | 6.7 ± 0.6 | 19.4 ± 1.2 | 5.4 ± 0.5 |
| fe[GluC3] | 4.7 ± 0.4 | 14.7 ± 0.8 | 5.0 ± 0.5 |
| fe[GlnC4] | 5.2 ± 0.6 | 16.7 ± 0.8 | 16.0 ± 2.4 |
| fe[GlnC3] | 3.7 ± 0.4 | 12.0 ± 0.7 | 7.9 ± 1.0 |
| fe[GlnC4]/fe[GluC4] | 0.78 ± 0.04 | 0.87 ± 0.04* | 2.90 ± 0.22** |
Metabolic modeling and TCA flux determinations
Figures 5A and B display the measured GluC4, GluC3, GluC2, GlnC4, GlnC3, GlnC2 time-courses as well as the corresponding best fits obtained for one individual experiment. The resulting fluxes were VTCAn = 0.50 ± 0.02 μmol/g/min and VTCAg= 0.15 ± 0.02 μmol/g/min (mean ± SD, n=9). These values are consistent with values reported elsewhere (Shen et al., 1999; Mason et al., 1999; Chhina et al., 2001; Chen et al., 2001; Lebon et al., 2002; Bluml et al., 2002). The overall TCA cycle rate is 0.65 μmol/g/min which is in the low range for the values of total VTCA reported for humans, the range being [0.57; 0.83] (for review see Hyder et al., 2006). We believe the explanation for the lower rate is the higher contribution of white matter to our VOI (approximately 53% white matter). Indeed, previous MRS studies have established a 3–4-fold lower TCA cycle rate in white matter compared to gray matter in human (Mason et al., 1999) and rat (de Graaf et al., 2004). We have obtained similar rates of metabolism using 13C-labeled glucose and acetate as tracers from this same volume (Boumezbeur et al., 2010).
FIG. 5.
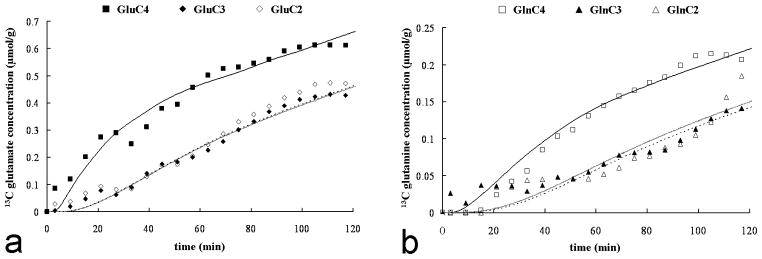
Time-courses of glutamate (A) and glutamine (B) 13C concentrations for the C4, C3 and C2 positions from one of the subjects during the infusion of [3-13C]lactate ([Lac]P ~ 2.7 mmol/L and 13C FE ~ 50%). The glutamate and glutamine C4 labeling are represented by squares (respectively close and open), while the glutamate C3 and C2 labeling by diamonds (respectively close and open) and glutamine C3 and C2 labeling by triangles (respectively close and open). The lines are the fits obtained with the metabolic model (C4: solid, dashed: C3, shaded: C2 positions). The scale for glutamine is increased approximately by a factor of 3 to facilitate the visualization of the kinetics.
Determination of lactate transport kinetics and net rate of lactate consumption
The measured values of Vin, [Lac]B and CMRlac are displayed in figure 6A, 6B and 6C along with their respective linear regressions. The following linear relationships were obtained: Vin=0.042.[Lac]P (R2=0.58); [Lac]B =0.63.[Lac]P (R2=0.75) and CMRlac=0.019.[Lac]P-0.007 (R2=0.71). To determine the range of values of VMAX and KT consistent with the results the curves were fit to the reversible Michaelis Menten model as described above and Monte Carlo analysis performed to determine the range of values consistent with the data. Based on this analysis the mean value of KT was 5.1 mmol/L with a 68% CI ranging from 2.4 to 7.8 mmol/L. As shown in figure 6D, the distribution of KT is not symmetrical with a skewness (G1) of 0.5. The mean and range of KT values are consistent with Vin being close to linear with the range of plasma lactate concentration studied (0.8 to 2.8 mmol/L) which encompasses the full range encountered in most physiological conditions. The mean value of VMAX was calculated to be VMAX=0.40 ± 0.13 μmol/g/min. The overlay of the probability density functions and corresponding histograms for KT and VMAX are shown in figure 6D.
Because the initial run of the metabolic modeling was performed assuming a KT value of 4.4 mmol/L, the metabolic modeling was performed again with KT set the following values: 2.4, 5.1 and 7.8 mmol/L corresponding to a 68% centered confidence interval. Consistently to the relations [7] and [10], the Vin and CMRlac values were found to remain largely unchanged as demonstrated by the figures 7A and 7B where individuals fluxes values obtained for KT = 2.4 and 7.8 mmol/L are compared (slopes~1.01, R2>0.99). Table 2 presents the VMAX and VMAX/KT ratios derived from the metabolic modeling of the individual datasets (mean±SD, n=9) for the different KT values considered.
Table 2.
VMAX values and VMAX/KT ratio obtained from the dynamic modeling of the individual datasets (mean±SD, n=9) for KT values being 2.4, 5.1 and 7.8 mmol/L. These KT values correspond to the mean-SD, mean and mean+SD values estimated from the Monte Carlo analysis (see figure 6D).
| KT (mmol/L) | Mean−SD | Mean | Mean+SD |
|---|---|---|---|
| 2.4 | 5.1 | 7.8 | |
| VMAX (μmol/g/min) | 0.25 ± 0.07 | 0.38 ± 0.10 | 0.50 ± 0.15 |
| VMAX/KT (/min) | 0.104 ± 0.028 | 0.074 ± 0.021 | 0.065 ± 0.019 |
DISCUSSION
Over the past decade, 13C MRS has been used to study cerebral metabolism in vivo mostly using 13C-labeled glucose (for reviews see Shen and Rothman, 2002; Hyder et al., 2006). However several studies have looked at the alternate substrates: acetate and β-hydroxybutyrate (Lebon et al., 2002, Pan et al., 2001). The results here demonstrate that 13C-labeled lactate can be used to study brain metabolism, and also establish lactate transport parameters and cell type preference for its consumption. In addition, they support that plasma lactate can potentially be a significant net fuel for brain metabolism under conditions of elevated plasma lactate or decreased plasma glucose.
Contribution of plasma lactate to brain metabolism
Using the measured values of plasma and intracellular lactate and Vin, CMRlac was estimated using equation [7] and is plotted in Figure 6C. At plasma lactate levels close to resting values, there is very little if any net consumption, consistent with previous AV difference studies (Siesjö, 1978). As plasma lactate concentration is elevated, CMRlac increases linearly with a ratio of CMRlac/VTCA~7% for the highest plasma lactate concentration studied ([Lac]P=2.8 mmol/L). Although CMRlac is relatively low, our results suggest that a further increase in [Lac]P or a decrease in [Lac]B can lead to substantially higher contributions to metabolism. Smith et al. (2003) found plasma lactate was able to replace approximately 17% of glucose uptake after blood lactate was elevated by lactate infusion corresponding to CMRlac~0.08 μmol/g/min for [Lac]P~4.1 mmol/L at euglycemia. Using either the best linear fit to CMRlac or the mean KT and VMAX to extrapolate to this higher lactate concentration a CMRlac flux of 0.07 μmol/g/min is predicted, consistent with the Smith et al. (2003) measurement. Studies have also shown high net lactate usage when it is elevated by hypoxia (Schurr, 1997a, 1997b) or following intense physical exercise (Kemppainen et al., 2005; van Hall et al., 2009).
The maximum rate of CMRlac as a function of [Lac]P can be determined from equations [7] and [8] with the assumption that intracellular lactate concentration is maintained near 0 by metabolism. In this case, CMRlac is equivalent to Vin:
| [11] |
The maximum rate is relevant for situations in which [Lac]B is low due to reduced glycolytic lactate production, which may occur during hypoglycemia. Figure 8 plots the maximum CMRlac vs. [Lac]P for the mean KT value and the values at the 68% CI. Above the mean value, there is very little influence of KT on the calculated maximum CMRlac. The mean value of VMAX was used. Under these conditions, the maximum contribution of plasma lactate to brain metabolism under normal plasma lactate concentrations near 1.0 mmol/L is predicted to be CMRlac/VTCA~10%. This contribution to brain energy production would be highly significant for avoiding brain energy failure under conditions of hypoglycemia that occur during fasting and for patients with type-1 diabetes after insulin injection, particularly if brain lactate transport is up-regulated by 2-fold as it has been reported for acetate by Mason et al. (2006). The VMAX for plasma lactate transport is high, and in principle could provide for as much as ~60% of the oxidative substrate needs of the occipital cortex at very high plasma levels (CMRlac=VMAX). Brain metabolism of plasma lactate could conceivably differ in other brain regions reflecting differences in activity of the relevant monocarboxylic acid tranporters.
FIG. 8.
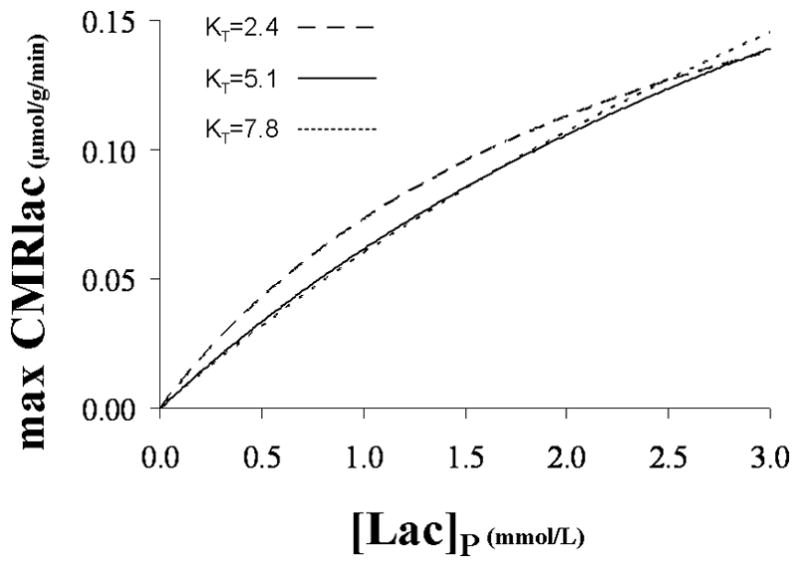
Maximum lactate consumption versus plasma lactate concentration for the mean KT value: 5.1 mmol/L, and the values at the 68% CI: 2.4 and 7.8 mmol/L. For each KT value, the corresponding mean VMAX value was considered: 0.25, 0.38 and 0.50 μmol/g/min (see Table 2).
In the study by van Hall et al. (2009), circulating lactate brain uptake and subsequent contribution to oxidative energy synthesis was estimated using AV difference. The brain went from a net release of lactate at rest ([Lac]P=0.9 mmol/L), to a net consumer during lactate infusion at levels of [Lac]P=3.9 mmol/L and [Lac]P=6.9 mmol/L. These results are consistent with our predictions of net lactate consumption as a function of [Lac]P. The lactate they infused was 13C-enriched at the C1 position and they assessed the fraction of lactate oxidized and its contribution to cerebral energy expenditure based upon the appearance of the 13C-label in CO2. At the three concentrations studied, they measured a contribution of lactate to total cerebral oxidative energy expenditure of 8%, 19%, and 27% which is in excellent agreement with the ratio calculated between the lactate entry and brain TCA cycle rates (Vin/VTCA) using our measured kinetic parameters (KT=5.1 mmol/L, VMAX=0.38 μmol/g/min): 8%, 21% and 28%. This agreement is due to the relative 13C-labeling of CO2 through PDH activity being proportional to the fractional enrichment of brain lactate/pyruvate pool (see [9] in Materials and Methods). We also note that the good agreement with AV difference studies suggests that our values obtained from the occipital lobe may be extrapolated to the cerebral cortex as a whole, although direct measurements will be needed to establish the generality conclusively.
Cellular compartmentation of lactate metabolism
Because glutamine is synthesized only in glial cells, whereas the majority of glutamate resides in neurons, analysis of [4-13C]glutamine/[4-13C]glutamate (fe[GlnC4]/fe[GluC4]) labeling ratios can give an insight into the metabolic compartmentation of a substrate (Pan et al., 2002), with higher ratios indicating greater percentages of substrate transport and oxidation in glia. In our study, this ratio for lactate as a substrate was 0.78 ± 0.04 (mean ± SD, n=9), similar to the ratio determined for [1-13C]glucose as substrate: 0.87 ± 0.04 (mean ± SD, n=7). In both cases, the ratios were determined for the same occipito-parietal location and from a matched group of healthy young subjects, consistent with the same distribution of usage in glia and neurons.
In contrast studies using [2-13C]acetate, a known glial substrate, exhibit fe[GlnC4]/fe[GluC4] ratios several fold higher. Based on previous 13C MRS studies that quantitated neuronal and glial glucose oxidation, the finding of similar labeling as observed with [1-13C] glucose suggests that there is similarly a 4-fold higher oxidation of plasma lactate in neurons than glia (Lebon et al., 2002; Boumezbeur et al., 2010). However a study using high resolution [14C]2-deoxyglucose autoradiography in combination with immune staining of neuronal and glial cell bodies suggested that glucose uptake is evenly distributed between these cell types (Nehlig et al., 2004). The [14C]2-deoxyglucose findings, which reflects total glucose uptake rather than oxidation, would not conflict with the present MRS findings should the lactate produced through glial glycolysis be oxidized mainly in the neurons, a point made by the study’s authors (Nehlig et al., 2004).
Recent studies suggest that lactate is more specific to neurons than glucose (Tyson et al., 2003; Qu et al., 2000). For example, Tyson et al. (2003) measured fe[GlnC4]/fe[GluC4] ratios closer to 0.67 for lactate vs. 0.92 for glucose. A potential explanation for this discrepancy is that, as discussed previously, glucose labeled at the C1 and C6 positions produced by gluconeogenesis from [3-13C]lactate resulted in labeling of brain glutamine and glutamate, obscuring the difference. Alternatively, it may reflect species differences. For now, we can only definitively conclude that at minimum plasma lactate is used by neurons and glia at a fraction similar to that of plasma glucose.
Evaluation of lactate transport kinetics
Kinetics for lactate transport were evaluated using a reversible Michaelis-Menten model. The reversible Michaelis-Menten kinetics have been described in detail (Mahler and Cordes, 1971; Cunningham et al., 1986) and used successfully to study glucose transport kinetics in human brain (Gruetter et al., 1998; de Graaf et al., 2001; Choi et al., 2001). Detailed kinetic modeling and meta-analysis of literature results by Simpson et al. (2007) have supported it as accurately describing brain glucose and monocarboxylic acid transport. As seen in figure 6A, Vin is close to linear with [Lac]P over the range studied. The mean KT of 5.1 mmol/L determined by Monte Carlo analysis agrees with this observation although there is a significant spread in the range of values consistent with results from previous studies of MCT1 in animal brain or oocytes which have found KT values of ~4 mmol/L (Bröer et al., 1998; Manning Fox et al., 2000).
Relevance to the astrocyte-to-neuron lactate shuttle
A major question regarding lactate metabolism is whether lactate produced in astrocytes by glycolysis is transferred to neurons for oxidation, often called the astrocyte-to-neuron lactate shuttle (ANLS). Although there is considerable evidence for the ANLS model (Magistretti et al., 1999; Pellerin et al., 2005), it remains to be shown directly that there is net transfer of lactate from glia to neurons in vivo. A prediction of the ANLS model is that lactate transport capacities of neurons and astrocytes are high enough to meet the energy demand of neurons. The finding that relative labeling of glutamine and glutamate from plasma-borne [3-13C]lactate is similar to that from [1-13C]glucose as substrate strongly suggests that neuronal and glial lactate pools have the same 13C fractional enrichment, implying that the relative lactate transport capacity of neurons and astroglia is either the same as their relative rates of glucose oxidation or much greater, creating effectively a single-shared lactate pool. Combined with the finding extrapolated from transport kinetics that plasma lactate can provide up to 60% of the brains oxidative requirements, our results suggest that cellular lactate transport is not likely to be limiting for an ANLS mechanism in human cerebral cortex.
Evaluation of 13C-labeled lactate as a metabolic tracer
As a general MRS tracer for studying brain metabolism, the primary limitation of lactate is that its labeling of the brain pyruvate pool is relatively low at physiological levels. For example as shown in Figure 4, several-fold higher 13C fractional enrichment was achieved using [1-13C]glucose rather than even the higher level of lactate in the present study. A second limitation of using lactate is that the production of labeled glucose from [3-13C]lactate via gluconeogenesis by liver is a potential complication in the metabolic modeling. Significant labeling of glucose in the C1 or C6 position was observed (2.8 ± 0.7 % for C1 and 2.4 ± 0.6 % for C6 above natural abundance; mean ± SD, n=9). Because of the delay in the appearance of glucose labeling (Figure 2D) and our incorporation of labeled glucose as a precursor in the metabolic modeling, its impact on the determination of metabolic rates and transport kinetics was not large. However, it may have obscured subtle differences between the cellular localization of lactate and glucose utilization. A potential solution would be the administration of insulin during the experiment in order to slow down the release in the bloodstream of labeled glucose from the liver. A final limitation is that elevated plasma sodium lactate is a well-known anxiogen used experimentally to provoke and study panic disorder (Cowley and Arana, 1990). In the present set of experiments, subjects did not report any symptoms related to anxiety during the infusion, most likely due to the low plasma lactate concentrations used. However care must be taken for this possibility which may restrict the level of lactate that can be explored experimentally.
CONCLUSION
In conclusion, the VMAX and KT of lactate metabolism demonstrate that the human brain has the capacity to support up to 10% of its energy metabolism with lactate under physiological levels and up to 60% under supra-physiological levels. The unidirectional transport of lactate is effectively linear over the physiological range and beyond. Neurons are the dominant source of plasma lactate metabolism, similar to what is observed with plasma glucose. Plasma lactate may be a significant net fuel for brain metabolism under conditions where plasma lactate is elevated such as after exercise or hypoxia/ischemia or when plasma glucose is reduced due to fasting hypoglycemia or following insulin administration. 13C MRS has the potential of directly studying brain lactate metabolism in these and other states where plasma lactate may be play an important role in sustaining brain function.
Acknowledgments
This work was supported by grants by R01-NS037527 (DLR), K02-AA13430 (GFM), R01-AG23686 (KFP) and P01-DK68229 (GIS, KFP, DLR), Howard Hughes Medical Institute (GIS), The Keck Foundation and NIH/NCRR/GCRC/M01-RR00125.
The authors thank Mikhail Smolgovsky, Yanna Kosover, Donna D’Eugenio, RN, Gina D’Agostino, RN and the Yale/New Haven Hospital General Clinical Research Center for their technical assistance; Terry Nixon, Peter Brown, and Scott McIntyre for maintenance and upgrades to the MRS system; the volunteers for their participation in these studies.
References
- Bachelard H. Landmarks in the application of 13C-magnetic resonance spectroscopy to studies of neuronal/glial relationships. Dev Neurosci. 1998;20:277–288. doi: 10.1159/000017322. [DOI] [PubMed] [Google Scholar]
- Bluml S, Moreno-Torres A, Shic F, Nguy CH, Ross BD. Tricarboxylic acid cycle of glia in the in vivo human brain. NMR Biomed. 2002;15:1–5. doi: 10.1002/nbm.725. [DOI] [PubMed] [Google Scholar]
- Boumezbeur F, Mason GF, de Graaf RA, Behar KL, Cline GW, Shulman GI, Rothman DL, Petersen KF. Altered brain mitochondrial metabolism in healthy aging as assessed by in vivo magnetic resonance spectroscopy. J Cereb Blood Flow Metab. 2010;30(1):211–221. doi: 10.1038/jcbfm.2009.197. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bröer S, Schneider HP, Bröer A, Rahman B, Hamprecht B, Deitmer JW. Characterization of the monocarboxylate transporter 1 expressed in Xenopus laevis oocytes by changes in cytosolic pH. Biochem J. 1998;333(1):167–174. doi: 10.1042/bj3330167. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen W, Zhu XH, Gruetter R, Seaquist ER, Adriany G, Ugǔrbil K. Study of tricarboxylic acid cycle flux changes in human visual cortex during hemifield visual stimulation using 1H-[13C] MRS and fMRI. Magn Reson Med. 2001;45:349–355. doi: 10.1002/1522-2594(200103)45:3<349::aid-mrm1045>3.0.co;2-8. [DOI] [PubMed] [Google Scholar]
- Chhina N, Kuestermann E, Halliday J, Simpson LJ, Macdonald IA, Bachelard HS, Morris PG. Measurement of human tricarboxylic acid cycle rates during visual activation by 13C magnetic resonance spectroscopy. J Neurosci Res. 2001;66:737–746. doi: 10.1002/jnr.10053. [DOI] [PubMed] [Google Scholar]
- Choi IY, Lee SP, Kim SG, Gruetter R. In vivo measurements of brain glucose transport using the reversible Michaelis–Menten model and simultaneous measurements of cerebral blood flow changes during hypoglycemia. J Cereb Blood Flow Metab. 2001;21:653–663. doi: 10.1097/00004647-200106000-00003. [DOI] [PubMed] [Google Scholar]
- Cohen SM. 13C NMR study of effects of fasting and diabetes on the metabolism of pyruvate in the tricarboxylic acid cycle and the utilization of pyruvate and ethanol in lipogenesis in perfused rat liver. Biochemistry. 1987;26:573–589. doi: 10.1021/bi00376a033. [DOI] [PubMed] [Google Scholar]
- Cowley DS, Arana GW. The diagnostic utility of lactate sensitivity in panic disorder. Arch Gen Psychiatry. 1990;47(3):277–284. doi: 10.1001/archpsyc.1990.01810150077012. [DOI] [PubMed] [Google Scholar]
- Cunningham VJ, Hargreaves RJ, Pelling D, Moorhouse SR. Regional blood-brain glucose transfer in the rat: a novel double-membrane kinetic analysis. J Cereb Blood Flow Metab. 1986;6:305–314. doi: 10.1038/jcbfm.1986.53. [DOI] [PubMed] [Google Scholar]
- de Graaf RA, Pan JW, Telang FW, Lee JH, Brown P, Novotny EJ, Hetherington HP, Rothman DL. Differentiation of glucose transport in human brain gray and white matter. J Cereb Blood Flow Metab. 2001;21:483–492. doi: 10.1097/00004647-200105000-00002. [DOI] [PubMed] [Google Scholar]
- de Graaf RA, Mason GF, Patel AB, Behar KL, Rothman DL. In vivo1H-[13C]-NMR spectroscopy of cerebral metabolism. NMR Biomed. 2003;16:339–357. doi: 10.1002/nbm.847. [DOI] [PubMed] [Google Scholar]
- de Graaf RA, Mason GF, Patel AB, Rothman DL, Behar KL. Regional glucose metabolism and neurotransmission in rat brain in vivo. Proc Natl Acad Sci U S A. 2004;101(34):12700–12705. doi: 10.1073/pnas.0405065101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gjedde A, Diemer N. Autoradiographic determination of regional brain glucose content. J Cereb Blood Flow Metab. 1983;3:303–310. doi: 10.1038/jcbfm.1983.45. [DOI] [PubMed] [Google Scholar]
- Gruetter R, Novotny EJ, Boulware SD, Mason GF, Rothman DL, Shulman GI, Prichard JW, Shulman RG. Localized 13C NMR spectroscopy in the human brain of amino acid labeling from D-[1–13 C]glucose. J Neurochem. 1994;63:1377–1385. doi: 10.1046/j.1471-4159.1994.63041377.x. [DOI] [PubMed] [Google Scholar]
- Gruetter R, Novotny EJ, Boulware SD, Rothman DL, Shulman RG. 1H NMR studies of glucose transport in the human brain. J Cereb Blood Flow Metab. 1996;16:427–438. doi: 10.1097/00004647-199605000-00009. [DOI] [PubMed] [Google Scholar]
- Gruetter R, Ugǔrbil K, Seaquist ER. Steady-state cerebral glucose concentrations and transport in the human brain. J Neurochem. 1998;70:397–408. doi: 10.1046/j.1471-4159.1998.70010397.x. [DOI] [PubMed] [Google Scholar]
- Gruetter R, Seaquist ER, Ugǔrbil K. A mathematical model of compartmentalized neurotransmitter metabolism in the human brain. Am J Physiol Endocrinol Metab. 2001;281:E100–E112. doi: 10.1152/ajpendo.2001.281.1.E100. [DOI] [PubMed] [Google Scholar]
- Harada M, Okuda C, Sawa T, Murakami T. Cerebral extracellular glucose and lactate concentration during and after moderate hypoxia in glucose- and saline-infused rats. Anesthesiology. 1992;77:728–734. doi: 10.1097/00000542-199210000-00017. [DOI] [PubMed] [Google Scholar]
- Hassel B, Sonnewald U, Fonnum F. Glial-neuronal interactions as studied by cerebral metabolism of [2–13C]acetate and [1–13C]glucose: an ex vivo13C NMR spectroscopic study. J Neurochem. 1995;64:2773–2782. doi: 10.1046/j.1471-4159.1995.64062773.x. [DOI] [PubMed] [Google Scholar]
- Henry PG, Oz G, Provencher S, Gruetter R. Toward dynamic isotopomer analysis in the rat brain in vivo: automatic quantitation of 13C NMR spectra using LCModel. NMR Biomed. 2003;16:400–412. doi: 10.1002/nbm.840. [DOI] [PubMed] [Google Scholar]
- Henry PG, Adriany G, Deelchand D, Gruetter R, Marjanska M, Öz G, Seaquist ER, Shestov A, Ugǔrbil K. In vivo13C NMR spectroscopy and metabolic modeling in the brain: a practical perspective. Magn Reson Imaging. 2006;24:527–539. doi: 10.1016/j.mri.2006.01.003. [DOI] [PubMed] [Google Scholar]
- Hetherington HP, Pan JW, Mason GF, Adams O, Vaughn MJ, Twieg DB, Pohost GM. Quantitative high-resolution spectroscopic imaging of human brain in vivo at 4.1T using image segmentation. Magn Reson Med. 1996;36:21–29. doi: 10.1002/mrm.1910360106. [DOI] [PubMed] [Google Scholar]
- Hyder F, Patel AB, Gjedde A, Rothman DL, Behar KL, Shulman RG. Neuronal-glial glucose oxidation and glutamatergic-GABAergic function. J Cereb Blood Flow Metab. 2006;26(7):865–877. doi: 10.1038/sj.jcbfm.9600263. [DOI] [PubMed] [Google Scholar]
- Kemppainen J, Aalto S, Fujimoto T, Kalliokoski KK, Långsjö J, Oikonen V, Rinne J, Nuutila P, Knuuti J. High intensity exercise decreases global brain glucose uptake in humans. J Physiol. 2005;568(Pt 1):323–332. doi: 10.1113/jphysiol.2005.091355. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lebon V, Petersen K, Cline GW, Shen J, Mason G, Dufour S, Behar KL, Shulman GI, Rothman DL. Astroglial contribution to brain energy metabolism in humans revealed by 13C nuclear magnetic resonance spectroscopy: elucidation of the dominant pathway for neurotransmitter glutamate repletion and measurement of astrocytic oxidative metabolism. J Neurosci. 2002;22:1523–1531. doi: 10.1523/JNEUROSCI.22-05-01523.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leenders KL, Perani D, Lammertsma AA, Heather JD, Buckingham P, Healy MJR, Gibbs JM, Wise RJS, Hatazawa J, Herold S, Beaney RP, Brooks DJ, Spinks T, Rhodes C, Frackowiak RSJ, Jones T. Cerebral blood flow, blood volume and oxygen utilization. Normal values and effect of age. Brain. 1990;113:27–47. doi: 10.1093/brain/113.1.27. [DOI] [PubMed] [Google Scholar]
- Lin AP, Shic F, Enriquez C, Ross BD. Reduced glutamate neurotransmission in patients with Alzheimer’s disease - an in vivo13C magnetic resonance spectroscopy study. MAGMA. 2003;16:29–42. doi: 10.1007/s10334-003-0004-x. [DOI] [PubMed] [Google Scholar]
- Magistretti PJ, Pellerin L, Rothman DL, Shulman RG. Energy on demand. Science. 1999;283(5401):496–497. doi: 10.1126/science.283.5401.496. [DOI] [PubMed] [Google Scholar]
- Mahler H, Cordes E. Biological Chemistry. New York: Harper and Row; 1971. [Google Scholar]
- Mangia S, Tkaáè I, Gruetter R, Van De Moortele PF, Giove F, Maraviglia B, Ugǔrbil K. Sensitivity of single-voxel 1H-MRS in investigating the metabolism of the activated human visual cortex at 7 T. Magn Reson Imaging. 2006;24:343–348. doi: 10.1016/j.mri.2005.12.023. [DOI] [PubMed] [Google Scholar]
- Manning Fox JE, Meredith D, Halestrap AP. Characterisation of human monocarboxylate transporter 4 substantiates its role in lactic acid efflux from skeletal muscle. J Physiol. 2000;529(2):285–293. doi: 10.1111/j.1469-7793.2000.00285.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maran A, Cranston I, Lomas J, Macdonald I, Amiel SA. Protection by lactate of cerebral function during hypoglycaemia. Lancet. 1994;343:16–20. doi: 10.1016/s0140-6736(94)90876-1. [DOI] [PubMed] [Google Scholar]
- Mason GF, Rothman DL, Behar KL, Shulman RG. NMR determination of the TCA cycle rate and α-ketoglutarate/glutamate exchange rate in rat brain. J Cereb Blood Flow Metab. 1992;12:434–447. doi: 10.1038/jcbfm.1992.61. [DOI] [PubMed] [Google Scholar]
- Mason GF, Gruetter R, Rothman DL, Behar KL, Shulman RG, Novotny EJ. Simultaneous determination of the rates of the TCA cycle, glucose utilization, α-ketoglutarate/glutamate exchange, and glutamine synthesis in human brain by NMR. J Cereb Blood Flow Metab. 1995;15:12–25. doi: 10.1038/jcbfm.1995.2. [DOI] [PubMed] [Google Scholar]
- Mason GF, Pan JW, Chu WJ, Newcomer BR, Zhang Y, Orr R, Hetherington HP. Measurement of the tricarboxylic acid cycle rate in human grey and white matter in vivo by 1H-[13C] magnetic resonance spectroscopy at 4.1T. J Cereb Blood Flow Metab. 1999;19:1179–1188. doi: 10.1097/00004647-199911000-00002. [DOI] [PubMed] [Google Scholar]
- Mason GF, Rothman DL. Graded image segmentation of brain tissue in the presence of inhomogeneous radio frequency fields. Magn Reson Imaging. 2002;20:431–436. doi: 10.1016/s0730-725x(02)00510-6. [DOI] [PubMed] [Google Scholar]
- Mason GF, Petersen KF, deGraaf RA, Kanamatsu T, Otsuki T, Rothman DL. A comparison of 13C NMR measurements of the rates of glutamine synthesis and the tricarboxylic acid cycle during oral and intravenous administration of [1–13C]glucose. Brain Res Brain Res Protoc. 2003;10(3):181–190. doi: 10.1016/s1385-299x(02)00217-9. [DOI] [PubMed] [Google Scholar]
- Mason GF, Petersen KF, Lebon V, Rothman DL, Shulman GI. Increased brain monocarboxylic acid transport and utilization in type 1 diabetes. Diabetes. 2006;55(4):929–934. doi: 10.2337/diabetes.55.04.06.db05-1325. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mason GF, Petersen KF, deGraaf RA, Shulman GI, Rothman DL. Measurements of the anaplerotic rate in the human cerebral cortex using 13C magnetic resonance spectroscopy and [1–13C] and [2- 13 C]glucose. J Neurochem. 2007;100(1):73–86. doi: 10.1111/j.1471-4159.2006.04200.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Michaelis T, Merboldt KD, Bruhn H, Hanicke W, Frahm J. Absolute concentrations of metabolites in the adult human brain in vivo: quantification of localized proton MR spectra. Radiology. 1993;187:219–227. doi: 10.1148/radiology.187.1.8451417. [DOI] [PubMed] [Google Scholar]
- Nehlig A, Wittendorp-Rechenmann E, Lam CD. Selective uptake of [14C]2-deoxyglucose by neurons and astrocytes: high-resolution microautoradiographic imaging by cellular 14C-trajectography combined with immunohistochemistry. J Cereb Blood Flow Metab. 2004;24(9):1004–1014. doi: 10.1097/01.WCB.0000128533.84196.D8. [DOI] [PubMed] [Google Scholar]
- Oldendorf WH. Carrier-mediated bloodbrain barrier transport of short-chain monocarboxylic organic acids. Am J Physiol. 1973;224:1450–1453. doi: 10.1152/ajplegacy.1973.224.6.1450. [DOI] [PubMed] [Google Scholar]
- Pan JW, Rothman DL, Behar KL, Stein DT, Hetherington HP. Human brain β-hydroxybutyrate and lactate increase in fasting-induced ketosis. J Cereb Blood Flow Metab. 2000;20:1502–1507. doi: 10.1097/00004647-200010000-00012. [DOI] [PubMed] [Google Scholar]
- Pan JW, Telang FW, Lee JH, de Graaf RA, Rothman DL, Stein DT, Hetherington HP. Measurement of β-hydroxybutyrate in acute hyperketonemia in human brain. J Neurochem. 2001;79:539–544. doi: 10.1046/j.1471-4159.2001.00575.x. [DOI] [PubMed] [Google Scholar]
- Pan JW, de Graaf RA, Petersen KF, Shulman GI, Hetherington HP, Rothman DL. [2,4–13C2 ]-beta- Hydroxybutyrate metabolism in human brain. J Cereb Blood Flow Metab. 2002;22(7):890–898. doi: 10.1097/00004647-200207000-00014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pellerin L, Bergersen LH, Halestrap AP, Pierre K. Cellular and subcellular distribution of monocarboxylate transporters in cultured brain cells and in the adult brain. J Neurosci Res. 2005;79:55–64. doi: 10.1002/jnr.20307. [DOI] [PubMed] [Google Scholar]
- Provencher S. Estimation of metabolite concentrations from localized in vivo proton NMR spectra. Magn Reson Med. 1993;30:672–679. doi: 10.1002/mrm.1910300604. [DOI] [PubMed] [Google Scholar]
- Qu H, Håberg A, Haraldseth O, Unsgårdd G, Sonnewald U. 13C MR spectroscopy study of lactate as substrate for rat brain. Dev Neurosci. 2000;22:429–436. doi: 10.1159/000017472. [DOI] [PubMed] [Google Scholar]
- Rothman DL, Magnusson I, Katz LD, Shulman RG, Shulman GI. Quantitation of hepatic glycogenolysis and gluconeogenesis in fasting humans with 13C NMR. Science. 1991;254(5031):573–576. doi: 10.1126/science.1948033. [DOI] [PubMed] [Google Scholar]
- Rothman DL, Novotny EJ, Shulman GI, Howseman AM, Petroff OA, Mason G, Nixon T, Hanstock CC, Prichard JW, Shulman RG. 1H-[ 13C] NMR measurements of [4- 13C]glutamate turnover in human brain. Proc Natl Acad Sci USA. 1992;89:9603–9606. doi: 10.1073/pnas.89.20.9603. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schurr A, Payne RS, Miller JJ, Rigor BM. Brain lactate, not glucose, fuels the recovery of synaptic function from hypoxia upon reoxygenation: an in vitro study. Brain Res. 1997a;744:105–111. doi: 10.1016/s0006-8993(96)01106-7. [DOI] [PubMed] [Google Scholar]
- Schurr A, Payne RS, Miller JJ, Rigor BM. Brain lactate is an obligatory aerobic energy substrate for functional recovery after hypoxia: further in vitro validation. J Neurochem. 1997b;69:423–426. doi: 10.1046/j.1471-4159.1997.69010423.x. [DOI] [PubMed] [Google Scholar]
- Shen J, Rycyna RE, Rothman DL. Improvements on an in vivo automatic shimming method (FASTERMAP) Magn Reson Med. 1997;38:834–839. doi: 10.1002/mrm.1910380521. [DOI] [PubMed] [Google Scholar]
- Shen J, Petersen KF, Behar KL, Brown P, Nixon TW, Mason GF, Petroff OAC, Shulman GI, Shulman RG, Rothman DL. Determination of the rate of the glutamate/glutamine cycle in the human brain by in vivo 13C NMR. Proc Natl Acad Sci USA. 1999;96:8235–8240. doi: 10.1073/pnas.96.14.8235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shen J, Rothman DL. Magnetic resonance spectroscopic approaches to studying neuronal: glial interactions. Biol Psychiatry. 2002;52(7):694–700. doi: 10.1016/s0006-3223(02)01502-0. [DOI] [PubMed] [Google Scholar]
- Siesjö BK. Brain energy metabolism. New York: John Wiley and Sons; 1978. [Google Scholar]
- Simpson IA, Carruthers A, Vannucci SJ. Supply and demand in cerebral energy metabolism: the role of nutrient transporters. J Cereb Blood Flow Metab. 2007;27(11):1766–1791. doi: 10.1038/sj.jcbfm.9600521. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith D, Pernet A, Hallett WA, Bingham E, Marsden PK, Amiel SA. Lactate: a preferred fuel for human brain metabolism in vivo. J Cereb Blood Flow Metab. 2003;23:658–664. doi: 10.1097/01.WCB.0000063991.19746.11. [DOI] [PubMed] [Google Scholar]
- Sokoloff L. Circulation and energy metabolism of the brain. In: Siegel GL, Agranoff BW, Albers RW, Molinoff PB, editors. Basic Biochemistry. New York: Raven Press; 1989. pp. 577–578. [Google Scholar]
- Tyson RL, Gallagher C, Sutherland GR. 13C-Labeled substrates and the cerebral metabolic compartmentalization of acetate and lactate. Brain Research. 2003;992:43–52. doi: 10.1016/j.brainres.2003.08.027. [DOI] [PubMed] [Google Scholar]
- van Hall G, Stromstad M, Rasmussen P, Jans O, Zaar M, Gam C, Quistorff B, Secher NH, Nielsen HB. Blood lactate is an important energy source for the human brain. J Cereb Blood Flow Metab. 2009;29:1121–1129. doi: 10.1038/jcbfm.2009.35. [DOI] [PubMed] [Google Scholar]