Combined LTP and LTD of Modulatory Inputs Controls Neuronal Processing of Primary Sensory Inputs

Abstract

A hallmark of brain organization is the integration of primary and modulatory pathways by principal neurons. However, the pathway interactions that shape primary input processing remain unknown. We investigated this problem in mouse dorsal cochlear nucleus (DCN) where principal cells integrate primary, auditory nerve input with modulatory, parallel fiber input. Using a combined experimental and computational approach, we show that combined LTP and LTD of parallel fiber inputs to DCN principal cells and interneurons, respectively, broaden the time window within which synaptic inputs summate. Enhanced summation depolarizes the resting membrane potential and, thus lowers the response threshold to auditory nerve inputs. Combined LTP and LTD, by preserving the variance of membrane potential fluctuations and the membrane time constant, fixes response gain and spike latency as threshold is lowered. Our data reveals a novel mechanism mediating adaptive and concomitant homeostatic regulation of distinct features of neuronal processing of sensory inputs.

Introduction

A common structural and processing motif consists of principal cells receiving and integrating inputs from two distinct pathways: a primary pathway synapsing on the basal dendrites (primary or feedforward pathway), and a secondary pathway synapsing on the apical dendrites (modulatory or feedback pathway) (Fig. 1A). This circuit organization is found in the hippocampus (Amaral, 1993), cortex (Crick and Koch, 1998; Larkum et al., 2009; Petreanu et al., 2009), thalamus (Sherman and Guillery, 1998), brainstem (Oertel and Young, 2004), cerebellum (Shepherd, 1990), and in the cerebellum-like circuits of the electrosensory system (Berman and Maler, 1999). The interaction between primary and modulatory pathways determines, in large part, the information transferred by the principal cell about its primary inputs (Remondes and Schuman, 2002; Ang et al., 2005; Jarsky et al., 2005; Dudman et al., 2007; Takahashi and Magee, 2009). Although modulatory pathways show robust long-term synaptic plasticity such as LTP and LTD (Harvey-Girard et al.; Doller and Weight, 1985; Colbert and Levy, 1992; Bell et al., 1997; Ito, 2001; Fujino and Oertel, 2003; Bastian et al., 2004; Tzounopoulos et al., 2004), a remaining challenge is to determine the role of this plasticity in controlling the neuronal processing of primary signals.

Fig. 1. Glycinergic Disynaptic Inhibition in the DCN.

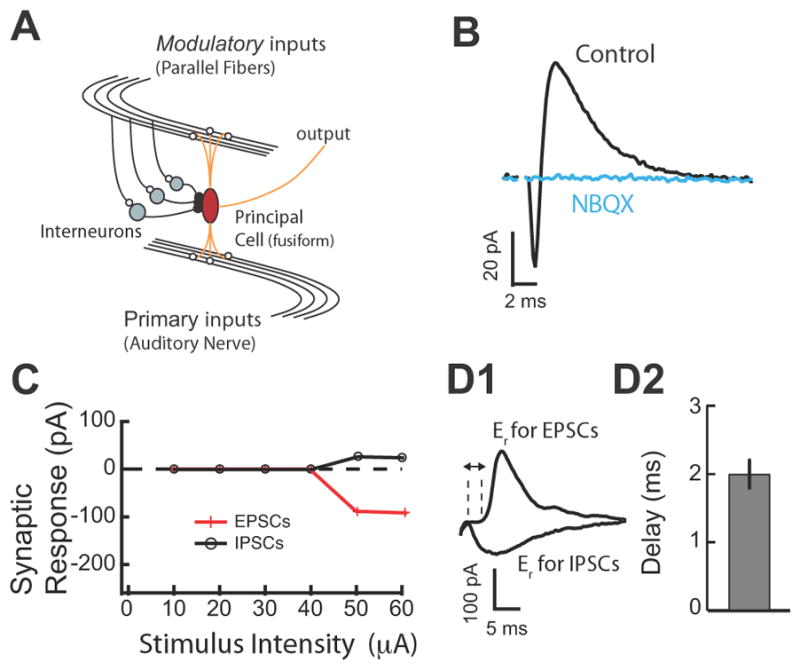
A. Schematic representation of general circuit motif where principal neurons integrate primary inputs with modulatory inputs (it is also labelled with the specific circuitry of the DCN). B. EPSC-IPSC sequence evoked in fusiform cells by parallel fiber (PF) stimulation. AMPA-type receptor antagonist (NBQX, 10 μM) blocked both inward (EPSC) and outward (IPSC) current, confirming the disynaptic origin of the IPSC. C. EPSC and IPSC amplitudes were plotted as a function of stimulus intensity. EPSC and IPSC have identical stimulus intensity thresholds. D1. Excitatory and inhibitory synaptic currents were separated by voltage clamping fusiform cells to the reversal for IPSC (−90 mV) and EPSC (5 mV), respectively. D2. The mean delay between the 10% rise time point of the EPSC and disynaptic IPSC was 2.0 ± 0.2 ms, n=8. Stimulus artifacts have been blanked for clarity in all traces. All means are reported ± SEM.

Three main features characterize the neuronal processing of primary inputs: threshold, gain and latency. Threshold is defined as the input strength that elicits an action potential with probability ½. Gain quantifies the sensitivity of the response to changes in input strength and latency denotes the time lag between primary input stimulation and spike response. Biophysical mechanisms that modulate threshold often change the net amount of synaptic input to a neuron, thereby affecting neuronal input resistance, membrane voltage fluctuations and membrane time constant (Silver; Chance et al., 2002; Cardin et al., 2008; Ly and Doiron, 2009). These biophysical changes are expected to simultaneously shift gain and latency. However, in vivo studies indicate that changes in threshold can occur without changes in gain (Tremblay and Schultz, 1999; Reynolds and Heeger, 2009). In addition, spike timing is crucial for many neuronal computations performed by sensory systems (Panzeri et al.; Grothe and Klump, 2000; VanRullen et al., 2005; Tiesinga et al., 2008) and must remain invariant during threshold adaptation, otherwise stimulus identification and discrimination is lost. While it is well understood how changes in modulatory synaptic input control threshold and gain (Silver, 2010), the circuit and cellular mechanisms that allow for adaptive threshold modulation of neuronal firing, with concomitant homeostatic control of gain and latency have not been uncovered.

We studied the effect of synaptic plasticity of modulatory inputs on the neuronal processing of primary sensory inputs in the dorsal cochlear nucleus (DCN). DCN principal cells integrate auditory signals (primary pathway) with multimodal signals (modulatory pathway) carried by descending parallel bers (Fig. 1A). Parallel ber excitatory inputs to principal cells exhibit LTP, while parallel ber inputs to feedforward inhibitory interneurons exhibit LTD (Tzounopoulos et al., 2004; Tzounopoulos et al., 2007; Zhao and Tzounopoulos, 2011). Our study unmasks a novel circuit mechanism that enables threshold modulation with simultaneous homeostatic control of gain and latency.

Methods

Electrophysiology

Pipette solution for current clamp contained (in mM) 113 K-gluconate, 1.5 MgCl₂, 14 trisphosphocreatine, 9 HEPES, 0.1 EGTA, 4 Na-ATP, 0.3 tris-GTP at pH 7.3. For voltage clamp experiments, pipettes were lled with a Cs⁺-based solution. The external solution contained in (mM) 130 NaCl, 3 KCl, 1.2 KH₂PO₄, 2.4 CaCl₂, 1.3 MgSO₄, 20 NaHCO₃, 3 HEPES, and 10 glucose; saturated with 95% O₂/5% CO₂. Coronal brain slices were made from ICR mice of either sex (P18–28). Animals were sacrificed according to methods approved by the Institutional Animal Care and Use Committee of University of Pittsburgh. Single cells were visualized with IR interference contrast optics and recorded using patch pipettes in either voltage- or current-clamp modes. Cells in the DCN’s fusiform cell layer were identified on the basis of morphological and electrophysiological criteria described in previous studies (Tzounopoulos et al., 2004).

Whole cell recordings were performed at 31–33°C. Given that parallel fiber (PF)-elicited disynaptic inhibition in fusiform cells is mediated by cartwheel cells, which use glycine as their principal transmitter (Mancilla and Manis, 2009), all electrophysiological experiments were performed in the presence of 20 μM SR-95531, an antagonist of GABA_A receptors. Golgi and stellate cells, the two other different interneuronal types found in the molecular layer of the DCN, are GABAergic and therefore were blocked in our experiments scheme (except for Fig. 3C, where glycinergic inhibition was blocked). This experimental design allowed us to determine the timing and the role of cartwheel-mediated disynaptic inhibitory inputs on synaptic summation, threshold, gain and latency. Parallel fibers responses were evoked by stimulating the molecular layer of the DCN (Tzounopoulos et al., 2004; 2007; Zhao and Tzounopoulos, 2011). Auditory nerve responses were evoked by stimulating the deep layer of the DCN (Fig. 5C). Electrical stimulation of deep layer activates excitatory auditory inputs arising from auditory nerve fibers and perhaps also auditory input from mulitipolar (D-type) cells (Oertel et al., 1990; Doucet and Ryugo, 2003; Oertel and Young, 2004). For current clamp experiments, input resistance was monitored from a response to a hyperpolarizing step during each sweep. Experiments were not included if the input resistance changed more than 20% over 50–60 min. For voltage-clamp experiments, series resistance was monitored throughout the experiment from the size and shape of the capacitive transient in response to a 5 mV hyperpolarization, after compensation of pipette capacitance. Input resistance was calculated from the sustained response to the same step. Experiments were not included if the series resistance changed more than 20% over 50–60 min. EPSC amplitude was defined as the mean amplitude during a 1–2 ms window at the peak of the EPSC minus the amplitude during a similar window immediately before the stimulus artifact. For LTP experiments, action potentials were evoked by somatic current injection. Post-pairing slope or amplitude was calculated from 20–25 min after the end of pairing. For combined LTP and WIN experiments (Fig. 3E, F) WIN was applied 2 minutes after delivering LTP induction protocol. All means are reported ± SEM. Statistical comparisons were made by unpaired two-tailed Student’s t-test. Statistical significance was based on p values <0.05.

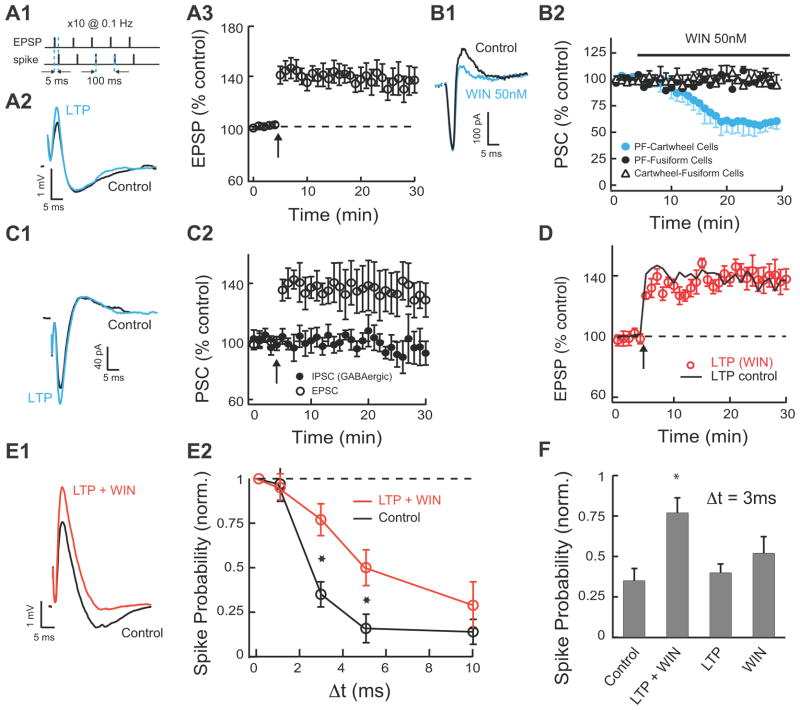
Fig. 3. Combined LTP and LTD Broadens the Timing Window within which Excitatory Inputs Summate.

A1. The LTP of excitatory input was induced by pairing of subthreshold EPSPs with current evoked spikes delivered 5 ms later. Our protocol included five such pairs delivered at 100 ms intervals followed by a 5-s pause, and repeated 10 times. A2 Example of averaged EPSP-IPSP responses in control and after stable LTP. LTP induced in fusiform cells increased only the EPSP in the EPSP-IPSP sequence. A3 The average time course of induced LTP of the EPSP (LTP 20–25 min after induction, 134.6% ± 9%, n=9). B1. 50 nM WIN reduces disynaptic IPSC, but does not reduce EPSC. B2. Time course of 50nM WIN effect on PF monosynaptic EPSCs to fusiform and cartwheel cells, and on glycinergic monosynaptic IPSCs on fusiform cells (direct IPSCs were evoked by direct stimulation of cartwheel cells in molecular layer and in the presence of 10 μM NBQX). Only EPSCs to cartwheel cells are reduced by WIN (PSC before/PSC 20–25 minutes after application of WIN: EPSCs to cartwheel cells: 59% ± 4%, n=9; EPSCs to fusiform cells: 99.6% ± 2%, n=6; monosynaptic IPSCs to cartwheel cells: 98% ± 3%, n=6). C1. Example of averaged EPSC-IPSC (GABAergic) responses before and 20–25 min after pairing of EPSPs and spikes as in A1 (glycinergic IPSCs were blocked with 0.5μM strychnine, no SR-95531 was applied for this experiment). Pairing protocol in fusiform cells increased only the EPSC in the EPSC-IPSC sequence. C2. The average time course of the EPSC and disynaptic IPSC (EPSC 20–25 min after induction: 134% ± 13%, n=6, p<0.05; IPSC 20–25 min after induction: 96% ± 11%, n=6). D. The average time course of induced LTP of the EPSP in the presence of WIN. Slices were incubated in 50 nM WIN for 1 hour prior to recording and 50 nM WIN was also bath applied during recording (LTP in WIN 20–25 min after induction, 138% ± 8%, n=5; LTP in control is in black line for comparison, same as in A3).

E1. Example of averaged EPSP-IPSP responses before and after combined LTP and 50 nM WIN application (EPSP-IPSP responses are shown before and 20–25 min post pairing protocol and WIN application. WIN was applied 2 minutes after delivering the LTP induction protocol (LTP 20–25 min after induction: 136% ± 8.5%, n=9; WIN-mediated depression 18–23 min after WIN application: 67% ± 7%, n=9). E2. Combined LTP and LTD widen the timing window for EPSP summation. Following induction of LTP in the fusiform cell and after waiting WIN application to reach a steady EPSP-IPSP response, stimulus intensity in path 2 was adjusted to return spike probability for synchronous stimulation to baseline. Data are means from 5–9 cells per point. F. Combined LTP and LTD are required for enlarging the timing window for EPSP summation. The response probability for Δt=3 ms is shown for control (35% ± 7%), LTP and LTD (77% ± 9%), LTP (40% ± 5), and LTD (52% ± 10%). Spike probabilities for E and F were measured 15–25 min post WIN application. Data are means from 5–7 cells per point. All means are reported ± SEM.

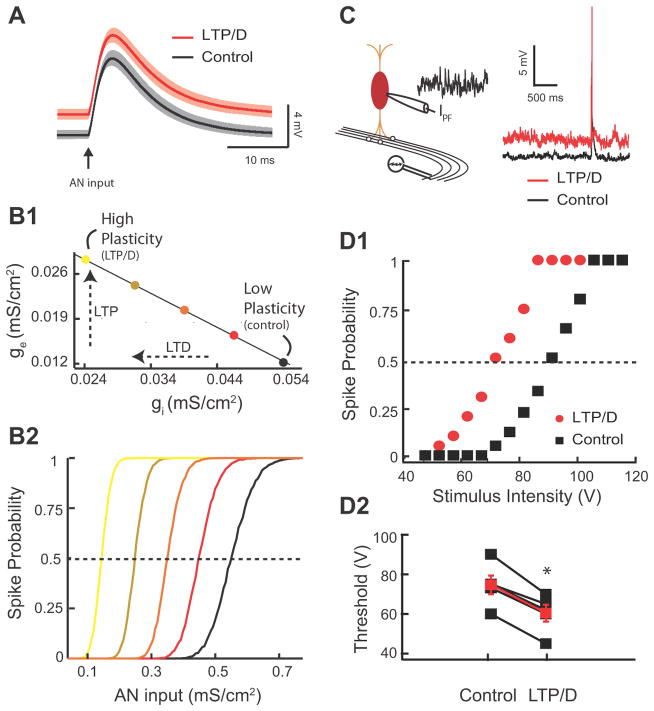
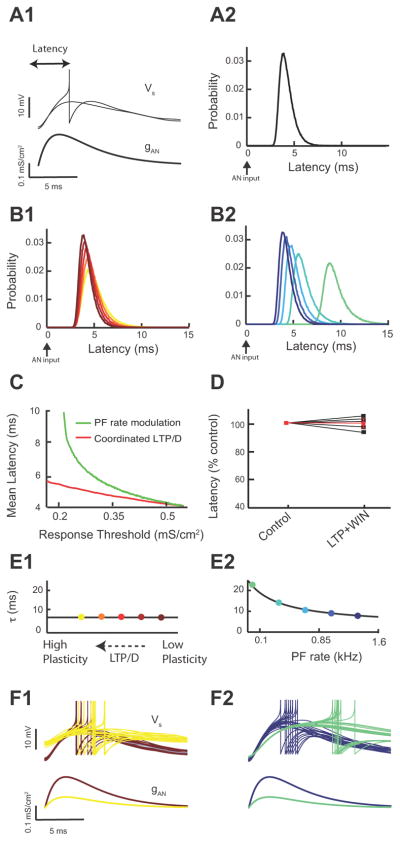
Fig. 5. Combined LTP and LTD Changes Threshold Response to Auditory Nerve Inputs.

(Panels A-B2 illustrate modelling data) A. Average model membrane response to an AN input in control (black trace) vs. combined LTP and LTD in control (red trace). Shaded areas are ± one standard deviation. B1. Application of the experimentally discovered combined LTP and LTD “path” on excitatory and inhibitory conductance. The coloured circles correspond to different levels of combined LTP and LTD. The g_e− g_i “path” is the extrapolated straight line linking the g_e−g_i experimentally derived pairs used in Figs 3F and 4A3. B2. Model of fusiform cell spike probability as a function of AN input strength (g_AN) for different levels of combined LTP and LTD modulation. The coloured circles correspond to different levels of combined LTP and LTD computed in (B1). The dashed line indicates the 0.5 probability response threshold.

(Panels C-D2 illustrate experimental data). C. Schematic representation of the placement of the stimulating electrode for stimulation of AN inputs (left). Representative traces from current clamp experiments showing of the ability of AN EPSPs to cause a spike in the fusiform cell during injection of simulated high frequency train of PSCs in control (black trace) or after simulation of combined LTP and LTD (red trace). D1. Representative current clamp experiment showing response probability of the same fusiform cell as a function of different AN stimulus intensity for control (black) and combined LTP and LTD (red). Control and combined LTP and LTD trains were the same as in Fig. 4D1, D2. D2. Changes of response threshold for 5 different fusiform cells in control and after combined LTP and LTD (control: 74.6 ± 4.7 V; LTP/D: 60.4± 4.2 V, p< 0.01, the red trace represents the average response). Threshold is the auditory input strength that elicits a response probability of 0.5.

Computational Model

We used a two-compartment exponential integrate-and-fire model (Pinsky and Rinzel, 1994; Koch, 1999; Fourcaud-Trocme et al., 2003) as a computational model of a fusiform cell:

$$\begin{array}{l}{C}_m\frac{{dV}_s}{dt}+g_L(V_s-E_L)+\frac{g_c}{\kappa }(V_s-V_d)=g_L\mathrm{\Delta }exp\left(\frac{V_s-V_T}{\mathrm{\Delta }}\right)+\frac{I_s(t)}{\kappa },\\ C_m\frac{{dV}_d}{dt}+g_L(V_d-E_L)+\frac{g_c}{1-\kappa }(V_d-V_s)=\frac{I_d(t)}{1-\kappa }.\end{array}$$

Here V_s and V_d are the somatic and dendritic membrane potentials, respectively. The passive membrane properties are determined by the membrane capacitance C_m, the membrane leak conductance g_L, and the leak reversal potential, E_L. Spiking dynamics were produced by the exponential term in the somatic current balance equation, giving a characteristic explosion to depolarized potentials when V_s sufficiently exceeds V_T. Electrotonic coupling was determined by the diffusive conductance, g_c, and the ratio of somatic to total membrane area, κ. In our model C_m=1 μF/cm², g_L=0.04 mS/cm², E_L=−67 mV, g_c=0.1 mS/cm², and κ=0.3. This yielded passive membrane time-constants of 1.93 ms and 25 ms (spiking term neglected); there are two membrane timescales because there are two compartments. Assuming a total cell area of 2.5×10⁻⁴ cm² (to give a cell capacitance of 250 pF) yields an “effective” membrane time-constant and input resistance of 23.9 ms and 117 MΩ, respectively (as measured from a step input to the soma). We set V_T=−58 mV and Δ=1.4 mV; when V_s > −30 mV a spike-time was recorded and the membrane was reset to −70 mV. The passive and spiking parameters are consistent with reported values from DCN fusiform cells recorded in vitro (Mancilla and Manis, 2009).

The somatic and dendritic synaptic inputs were decomposed as:

$$\begin{array}{l}{I}_s(t)=g_{\mathit{PFi}}(t)(E_i-V_s)+g_{AN}(t)(E_i-V_s)+\sigma \eta (t),\\ I_d(t)=g_{\mathit{PFe}}(t)(E_e-V_d).\end{array}$$

Here g_PFI and g_PFe are the inhibitory and excitatory conductances from PF synaptic activation, respectively; g_AN is the excitatory conductance of AN synaptic input. Synaptic reversal potentials were set to E_i=−90 mV and E_e=0 mV. η(t) is a weak low pass filtered Gaussian white noise (τ=2 ms and σ=0.05 μA/cm²), modelling high frequency intrinsic membrane fluctuations. The PF firing times were modelled as a high frequency Poisson processes, and the PF synaptic conductances were convolutions of the PF spike train with an appropriate synaptic filter:

$$g_{\mathit{PFe}}(t)=K_{\mathit{PFe}}(t)\ast {\sum }_i\delta (t-t_i);g_{\mathit{PFi}}(t)=K_{\mathit{PFi}}(t)\ast {\sum }_i\delta (t-t_i-{\tau }_{\mathit{delay}}),$$

The delay time between activation of excitatory and inhibitory PF inputs, τ_delay, was set to 2ms, based on our experimental measurements (Fig. 1D). The AN synapse fired only once, at time t_AN, so that g_AN(t)=K_AN(t−t_AN). In all cases the synaptic filters were the difference of exponentials scaled by a maximal channel conductance

$$K_X(t)={\overline{g}}_X\left(exp\left(-t/{\tau }_{1X}\right)-exp\left(-t/{\tau }_{2X}\right)\right).$$

Throughout, we set τ_1PFe=1.5 ms, τ_2PFe=0.25 ms, τ_1PFi=7 ms, τ_2PFi=2.1 ms, τ_1AN=4 ms, τ_2AN=1.33 ms. The AN input models the near synchronous activation of a population of synapses driven by the afferent AN nerve; the strength of ḡ_AN represented the number of synapses recruited in the population. LTP and LTD of the PF inputs to fusiform cells and cartwheel cells, respectively, were phenomenologically modelled as a respective increases and decreases of ḡ_PFe and ḡ_PFi, respectively. Simulations of the spiking system were performed in MATLAB with a custom-built C code (Mex) using a standard stochastic Euler-Maruyama integration scheme (dt=0.005 ms). Response probability and mean latency were determined from 5000 realizations of the model neuron with t_AN=125 ms. Response threshold values were defined as the value of ḡ_AN that yielded a 0.5 probability of firing after t_AN, a bisection algorithm was used to determine threshold with a tolerance of 0.01. We used a two-compartment model; our results are equally valid for a simple, one compartment LIF model (not shown).

Results

Disynaptic Inhibition Determines the Temporal Window During Which Excitatory Inputs Summate

Recordings were made from single fusiform and cartwheel cells in coronal slices of mouse DCN. Cell types were identified by their location in the molecular layer of the DCN and by their characteristic response to current injection (Zhang and Oertel, 1993; Manis et al., 1994; Tzounopoulos et al., 2004). To determine the effect of combined LTP and LTD of modulatory inputs on threshold, gain and spike latency in response to primary inputs, we first characterized disynaptic inhibition in the molecular layer of the DCN and its effects on synaptic summation. In fusiform cells, parallel fiber stimulation evoked a typical biphasic response consisting of a short latency excitatory postsynaptic current (EPSC) followed by an inhibitory postsynaptic current (IPSC) (Fig. 1B, Zhao et al., 2009). The α-amino-3-hydroxy-5-methyl-4-isoxazolepropionic acid (AMPA) glutamate receptor antagonist (NBQX, 10 μM) blocked the EPSC and the IPSC, confirming that the inhibitory component represents disynaptic inhibition (Fig. 1B). Next, we determined the timing of the onset of the disynaptic IPSC with respect to the EPSC.

Previous studies have established that it is difficult to interpret the timing of disynaptic IPSCs that have different stimulus intensity thresholds from EPSCs (Blitz and Regehr, 2005). Therefore, we used EPSCs and IPSCs that had identical stimulus intensity thresholds (Fig. 1C). Identical stimulus intensity threshold for EPSCs and IPSCs indicates that the same set of parallel fibers activates cartwheel cells (mediating disynaptic inhibition) and the recorded fusiform cell. Previous studies suggest that synchronous activation of ~8–16 fibers can drive spiking in cartwheel and fusiform cells (Roberts and Trussell). Thus, in agreement with previous in vivo and in vitro studies (Davis et al., 1996; Roberts and Trussell, 2010), our results indicate that the stimulated set of parallel fibers drives spiking in cartwheel cells and that the same set of fibers provides disynaptic, feedforward inhibition in the recorded fusiform cells. We isolated PCSs by voltage clamping at their respective reversal potentials. When cells were held at the reversal potential for glycine-mediated responses, a short latency inward EPSC was observed (Fig. 1D1) when cells were held at the reversal potential for glutamate-mediated responses the longer latency outward glycinergic IPSC was observed (Fig. 1D1). EPSCs and IPSCs were temporally distinct: IPSC onset followed EPSC onset by an average of ~ 2 msec (Fig. 1D2). These results are consistent with in vivo studies showing that the latency of inhibitory responses to DCN cells by electrical stimulation of trigeminal nerve (which provides input to granule cells giving rise to parallel fibers) is on average ~ 3 ms slower than the latency of the excitatory responses (Shore, 2005). Taken together these results indicate that parallel fiber stimulation elicited monosynaptic excitation and temporally precise feedforward disynaptic inhibition.

Previous studies have established that temporally precise inhibition determines the duration of the integration window over which excitatory inputs summate (Berman and Maler, 1998; Pouille and Scanziani, 2001; Wehr and Zador, 2003; Gabernet et al., 2005; Lamsa et al., 2005; Mittmann et al., 2005). To determine the integration window of fusiform cells, two independent parallel fiber inputs were stimulated (Fig. 2A1). The independence of pathways was tested in every experiment by paired-pulse facilitation. The second pair of shocks induced facilitation in the responses to stimuli of the same path, but not when pathways were separate and independent (Tzounopoulos et al., 2004). The stimulus intensity was adjusted so that when each pathway was stimulated alone the synaptic response remained subthreshold (Fig. 2A2), while spiking was elicited in ~50% of trials when the two pathways were stimulated synchronously (Fig. 2B, Δt= 0ms). For a fixed inter-stimulus interval (Δt) between the two pathways, we estimated the probability of fusiform cell spike response. The spike probability dropped significantly for Δt between 1 and 3 ms (Fig. 2C black). Given that the short duration of the integration window tracks the time course of the inhibitory component (Fig. 2C black vs. Fig. 1D), we hypothesized that feedforward disynaptic inhibition determines the duration of the integration window in fusiform cells. To test this hypothesis, we blocked disynaptic inhibition with strychnine (Fig. 2C inset) and measured the integration window. Indeed, a greatly prolonged integration window was observed when inhibition was blocked (Fig. 2C gray), indicating that glycinergic disynaptic inhibition determines the duration of the fusiform cell integration window over which parallel fiber inputs summate.

Fig. 2. Disynaptic Inhibition Determines Synaptic Summation of Excitatory Inputs in the DCN.

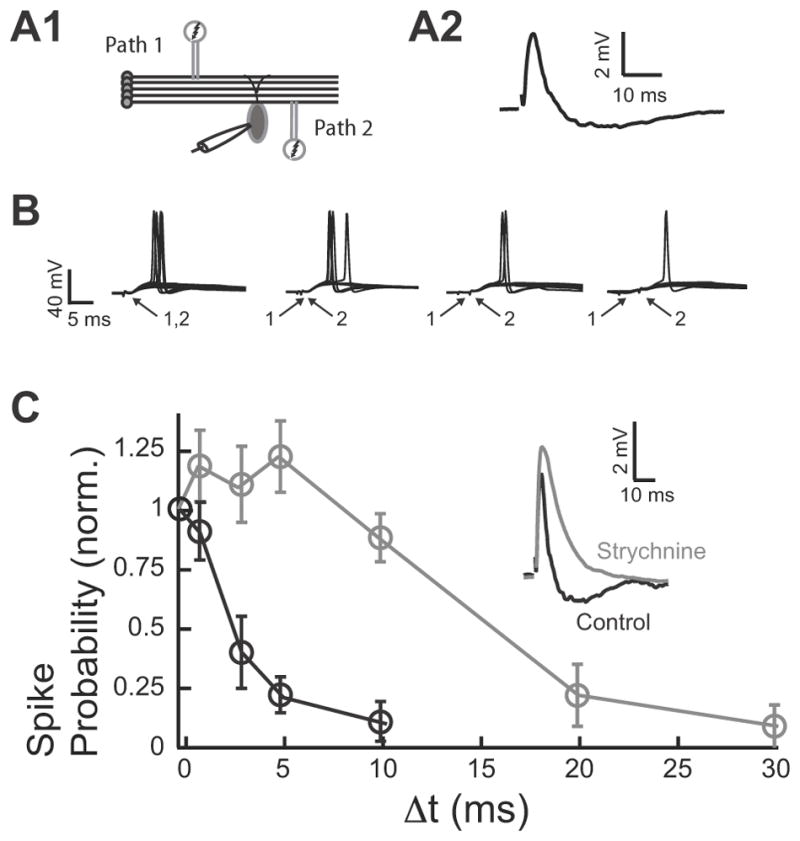
A1. Two-pathway experiment diagram. A2. Example of subthreshold EPSP/IPSP evoked by PF stimulation. B. Two independent PF (modulatory) inputs (the first one always showing EPSP-IPSP sequence as shown in A2) were stimulated either simultaneously (Δt=0), or 1, 3 and 5 ms apart. Stimuli were adjusted to produce an action potential upon synchronous stimulation in ~ 50% of trials (10 repetitions are shown for each time interval). C. The average spike probability fell steeply when the two stimuli were not delivered synchronously (Δt >0). The probability for each cell was normalized by the probability obtained for Δt=0. Blocking glycinergic transmission with strychnine (500 nM) abolished the disynaptic IPSP (inset). Blockade of disynaptic inhibition widened the timing window for EPSP summation. Timing window for control is in black and timing window after strychnine is in gray. Data are means from 5–9 cells per point. All means are reported ± SEM

Combined LTP and LTD Enlarges the Integration Window During Which Excitatory Inputs Summate

Our previous studies have demonstrated different forms of spike timing-dependent synaptic plasticity (STDP) at parallel fiber inputs onto fusiform and inhibitory (cartwheel) interneurons (Tzounopoulos et al., 2004; Tzounopoulos et al., 2007). In fusiform cells, spikes evoked 5 ms after parallel fiber EPSPs lead to Hebbian LTP, while the same EPSP-spike protocol leads to “anti-Hebbian”, endocannabinoid-mediated, LTD in cartwheel cells (Tzounopoulos et al., 2004; Tzounopoulos et al., 2007). Given that the same set of parallel fibers activates catrtwheel and fusiform cells that can lead to a compound PSP in fusiform cells (EPSP-IPSP sequence, Fig 1A), pairing of parallel fiber activation with postsynaptic spikes is expected to lead to LTP at the EPSP and LTD at the IPSP. However, the combined effect of Hebbian LTP and anti-Hebbian LTD (termed combined LTP and LTD) on the duration of the integration window has not been examined. Understanding the effect of combined plasticity is critical for determining the effect of circuit-level plasticity of parallel fiber pathway on the processing of auditory nerve inputs.

LTP of excitatory parallel fiber inputs onto fusiform cells was induced by pairing subthreshold EPSPs with current evoked spikes delivered 5 ms later (Fig. 3A1–A3, see also Materials and Methods). Anti-Hebbian LTD is expressed presynpatically via activation of cannabinoid receptors (CB1Rs, Tzounopoulos et al., 2007; Zhao and Tzounopoulos, 2011) and therefore was induced by application of low concentrations of WIN-55, 212-2 (WIN 50 nM, CB1R agonist). Paired recordings from synaptically coupled fusifrom neurons and cartwheel cells was not adequate to unmask the role of combined LTP and LTD. Paired-recordings induced LTD only on one cartwheel cell. Therefore, electrically induced LTD during paired-recordings (pairing of EPSPs and spikes as in Tzounopoulos et al., 2004, 2007) affected only a small part of the evoked disynaptic inhibition of the recorded fusiform cell, as multiple cartwheel cells innervate one fusiform cell (Mugnaini, 1985; Mancilla and Manis, 2009; Roberts and Trussell, 2010). Furthermore, electrical stimulation of parallel fibers produced inconsistent effects on the plasticity of parallel fibers inputs to fusiform and to cartwheel cells. Electrical stimulation of parallel fibers cannot control the specific timing requirements of pre- and postsynaptic activity that leads to cell-specific plasticity rules and to combined LTP and LTD (Tzounopoulos at al., 2004; Tzounopoulos et al., 2007). This finding is consistent with previous results, where electrical stimulation failed to unmask cell-specific plasticity in fusiform and cartwheel cells (Fujino and Oertel, 2003). To address these issues and to induce LTD in the cartwheel cells innervating the recorded fusiform cell, we used WIN. Consistent with our previous studies (Tzounopoulos et al., 2007; Zhao et al., 2009) WIN-mediated depression of parallel fiber inputs to cartwheel cells was similar in magnitude and in input-specificity (only parallel fiber inputs to cartwheel cells were inhibited by 50 nM WIN; Fig. 3B1, B2) with the electrically-induced, anti-Hebbian LTD observed in cartwheel cells (Tzounopoulos et al., 2004; Tzounopoulos et al., 2007), thus allowing us to use WIN for inducing anti-Hebbian LTD.

Combined (electrically-induced) LTP and (WIN-mediated) LTD is expected to increase the ratio of excitation over inhibition, and potentially lead to changes in the integration window. However, fusiform cells receive inhibitory synapses from stellate cells on the same dendritic region where they receive excitatory parallel fiber input, but this inhibition is pharmacologically blocked during combined LTP and LTD. We show that GABAergic inhibition is unaltered during parallel fiber LTP (Fig. 3C1, C2). Pairing subthreshold EPSPs with current evoked spikes delivered 5 ms later induced LTP at parallel fiber EPSCs, but it did not affect disynaptic GABAergic IPSCs (glycinergic inhibition was pharmacologically blocked, Fig. 3C2). These results suggest that GABAergic inhibition during parallel fiber LTP is not expected to uncouple combined LTP and LTD.

In addition, application of WIN did not affect the amount of electrically induced LTP (Fig. 3D), thus allowing us to study the combined effect of (electrically-induced) LTP and (WIN-mediated) LTD on the duration of the integration window, by employing simultaneous application of the LTP induction (pairing) protocol and 50 nM WIN. The combination of LTP pairing protocol and WIN application led to an increased EPSP and a decreased disynaptic IPSP respectively (Fig. 3E1). In agreement with the control experiment described in Fig. 3D, the amount of induced LTP and WIN-mediated LTD during combined LTP induction and WIN application (Fig. 3E1) did not differ either from the amount of LTP in the absence of WIN (Fig. 3A2) or from the amount of WIN-mediated depression in the absence of LTP induction protocol (Fig. 3B1). The integration window after induction of combined LTP and LTD had a significantly increased probability of spiking for intervals between 3 and 10 ms compared to that measured in control conditions (Fig. 3E2). This is an unexpected result as in all other cases reported in the literature (Lamsa et al., 2005; Froemke et al., 2007; Mittmann and Hausser, 2007), plasticities of similar sign cancel each others effect and have been thought to maintain fixed integration window (Lamsa et al., 2005). Actually, previous findings have led to a general idea that LTP and LTD maintain temporal fidelity of input discrimination (Lamsa et al., 2005). However, our data expands the role of LTP and LTD on synaptic summation and unmasks a novel concept according to which, combined LTP and LTD modulate the integration window in an activity dependent manner.

In contrast to combined LTP and LTD, when LTP or LTD were induced separately, they did not increase the probability of spike compared to control when Δt=3ms, indicating that the impact of LTP or LTD alone is not sufficient for enlarging the duration of the integration window (Fig. 3F). These results show that a reduction of inhibition does not have as large an effect as the combined effect of potentiation of excitation and depression of inhibition. This is a surprising finding given the role of inhibition in determining the duration of the integration window (Fig. 2C). Therefore, we conclude that “physiologically” observed levels of LTD do not produce enlarged integration window unless they occur in coordination with LTP (Fig. 3F). In total, these results indicate that combined LTP and LTD shifts the balance of excitation and inhibition towards excitation and increases synaptic summation by broadening the integration window of fusiform cells.

Increased Synaptic Summation on the Parallel Fiber Circuit Gates Auditory Nerve Inputs

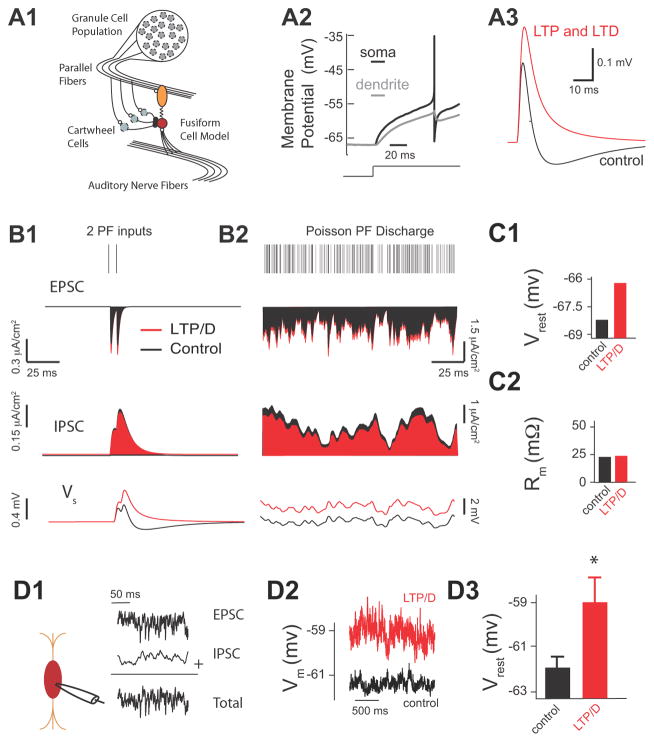
Two-pathway experiments were necessary to quantify the effect of combined LTP and LTD on the duration of the integration window and on the summation of pairs of synaptic inputs in vitro. However, during in vivo conditions fusiform cells summate multiple PSPs caused by the irregular firing of a population of granule cells. It is impossible to activate multiple parallel fiber inputs (pathways) in an asynchronous fashion with the traditional anatomically independent pathway experimental approach (assessed by paired pulse facilitation). Thus, we used a spiking model of a fusiform cell to examine the effect of combined synaptic plasticity on summating inputs from a population of granule cells (Fig. 4A, see also Materials and Methods). This approach allows an investigation of how multiple fiber inputs provide a “background”, fluctuating synaptic drive that acts to modulate the response to auditory nerve input ((Chance et al., 2002). In our model, fusiform cells received input from parallel fibers, and from auditory nerve fibers (Fig. 4A1). To account for the distinct spatial projections of excitation and inhibition along the somatodendritic axis (Rubio and Juiz, 2004), we used a two-compartment model of a spiking neuron. The somatic compartment is responsible for spike initiation and spike reset, while the dendritic compartment passively filters inputs (Fig. 4A2). Simulated combined LTP and LTD elicited EPSP-IPSP sequences matching experimental results (compare Fig. 4A3 with Fig. 3E1).

Fig. 4. Combined LTP and LTD of Parallel Fiber Inputs Depolarizes Fusiform Cells.

(Panels A1–C2 illustrate modelling data). A1. Two-compartment fusiform cell model driven by both auditory nerve (AN) activity and PF inputs arising from a population of granule cells. The PF excitatory inputs synapse onto the dendrite and PF inhibitory inputs and AN inputs synapse onto the soma. A2. The model spike response to a depolarizing step in input current. A3. The model membrane response to the mixed direct PF excitatory and indirect cartwheel inhibitory input with control synapse parameters (g_e=0.009 mS/cm² and g_i=0.0162 mS/cm², black curve) and with combined LTP and LTD synapse parameters (g_e=0.0115 mS/cm² and g_i=0.014 mS/cm², red curve). B1. Model EPSC (top), IPSC (middle) and fusiform cell membrane response (bottom) to two PF inputs (control synapse parameters are shown in black, and combined LTP and LTD synapse parameters in red). B2. Same as (B1) but now in response to a high frequency Poisson distributed PF discharge (1.6KHz). C1. Average resting model membrane potential (V_rest) for control vs. LTP/D synapse parameters during high frequency Poisson drive of PF shown in (B2). C2 Average model input resistance R_m for the same conditions as (C1).

(Panels D1–D3 illustrate experimental data) D1. Schematic representation of the placement of recording pipette (left) allowing injection of simulated high frequency train (control) of PSCs (EPSCs + IPSCs) mimicking PF activity shown in B2. D2. Current clamp experiments showing membrane potential measurements of fusiform cells in response to simulated PF activity in control (black trace) and after application of combined LTP and LTD in simulated trains (red trace). Recruitment of combined LTP and LTD was produced by modulating the injected control train of PSCs by enhancing EPSCs and reducing IPSCs by the percentage that was determined by our in vitro experiments shown in Fig. 3F. D3. Average resting membrane potential in response to simulated PF activity shown in D1 and D2 for control (−62± 0.5 mV, n=5) and after application of combined LTP and LTD (−59 ± 1 mV, n=5, p<0.01).

Our model reproduced our experimental findings showing that combined LTP and LTD caused an overall increase of EPSCs and an overall decrease of IPSCs (Fig. 4B1, top and middle), which enhanced the summation of PSPs elicited by activation of two parallel fiber inputs (Fig. 4B1, bottom). While in vivo recordings from DCN granule cells have not been obtained, cerebellar granule cells have low spontaneous firing (Chadderton et al., 2004). Given the strong parallels between DCN and cerebellum (Oertel and Young, 2004), the frequency of parallel fiber firing rate that was used in our model (Fig. 4B2, top) reflects convergent projections of a population of lower firing rate granule cells onto the fusiform-cartwheel cell circuit (Fig. 4A1). Simulation of combined LTP and LTD leads to a depolarization of the resting membrane potential (Fig. 4B2 bottom; Fig. 4C1). Taken together, our modelling findings indicate that combined LTP and LTD enhances the summation of multiple synaptic inputs, which results in a depolarization of the fusiform cell resting membrane potential.

To test experimentally the predicted effect of combined LTP and LTD on resting membrane potential, we needed to activate multiple parallel fiber inputs in a statistically independent fashion. Because electrical stimulation of parallel fibers is not appropriate for activating a large number of parallel fiber inputs in an asynchronous manner, we injected a train of simulated subthreshold excitatory and inhibitory input in fusiform cells (Fig. 4D1). This train (control) matched the Poisson distributed parallel fiber discharge shown in Fig. 4B2. Since, our model simulations predicted no changes in input resistance before and after the induction of combined LTP and LTD (Fig. 4C2), this allowed us to use current clamp methods to determine the effect of combined LTP and LTD on the average membrane potential. In response to our simulated parallel fiber inputs, the fusiform cell membrane potential fluctuated within a range of around 1 mV (Fig. 4D2 black). Recruitment of combined LTP and LTD was simulated by modulating the injected (control) train of PSCs (EPSCs were enhanced and IPSCs were reduced by a fixed percentage that was determined by our in vitro experiments shown in Fig. 3E1). Injection of PSCs simulating the effect of combined LTP and LTD caused an average ~3 mV depolarization of resting membrane potential (Fig. 4D2 red, 4D3), which is in close agreement with our model predictions (Fig. 4C1). These results indicate that the active conductances shaping the intrinsic properties of fusiform cells (Kanold and Manis, 1999) do not prevent the plasticity-induced depolarization predicted by our simplified integrate- and-fire model.

The fusiform cell depolarization induced by combined LTP and LTD is expected to affect the neuronal processing of auditory nerve inputs. To test this hypothesis we used a combined modelling and experimental approach. In our model, auditory nerve inputs were simulated with a transient, large amplitude synaptic conductance (Fig. 5A). Our model simulations revealed that combined LTP and LTD modulated the response to an auditory nerve input by a simple depolarization of the membrane potential (Fig. 5A, black vs. red). The depolarization is expected to reduce the spike response threshold to auditory nerve inputs with “fixed” synaptic strength (auditory nerve inputs do not show synaptic plasticity, Fujino and Oertel, 2003; Zhao and Tzounopoulos, 2011; Zhao et al., 2011). Our model simulations, in agreement with this hypothesis, show that recruitment of increasing amount of combined LTP and LTD (Fig. 5B1) decreased the spike response threshold of the fusiform cell to auditory nerve inputs (Fig. 5B2). Here and throughout the study, threshold is the input strength with a 50% chance of eliciting a spike. Thus, our modelling results predict that combined LTP and LTD of parallel fiber inputs reduces spike response threshold to auditory nerve inputs.

To test experimentally the predicted modulatory effect of parallel fiber synaptic plasticity on auditory nerve inputs, we simulated parallel fiber synaptic activity by injecting a train of subthreshold PSCs into a fusiform cell (as in Fig. 4D1–D3), while we simultaneously stimulated the deep layer of the DCN (Fig. 5C, left) to evoke auditory nerve-mediated EPSPs and spike responses (Fig. 5C right). We generated input-output curves by changing the intensity of auditory nerve stimulation and measuring spike probability of fusiform cells in control and after combined LTP and LTD (Fig. 5D1). Simulation of combined LTP and LTD (as in Fig. 4D2) shifted the threshold of auditory nerve inputs to lower stimulation intensity, thus validating experimentally our model simulations (Fig. 5D1, D2). The qualitative and quantitative agreement between model and experiment (compare Fig. 4C1 to Fig. 4D3 and Fig 5B2 to Fig. 5D1) supports the plausibility and the robustness of combined LTP and LTD as a mechanism in modulating threshold response to auditory nerve inputs during physiological conditions. Had the simulated EPSC/IPSC train produced a smaller depolarization in our experiments compared to the model, due to a small input resistance or to recruitment of hyperpolarizing currents in the fusiform cell, then our proposed mechanism would have required a much larger, “non-physiological”, recruitment of LTP and LTD or would be relevant only for much higher parallel fiber firing rate. In total, combined LTP and LTD of the parallel fiber circuit brings the synaptic response of auditory nerve inputs closer to spike threshold and thus decreases response threshold to auditory nerve inputs. This finding illustrates how a simple modulatory circuit and its adaptive synaptic properties provide a novel plasticity rule that allows for the gating of otherwise fixed sensory signals.

Combined LTP and LTD Preserves Gain by Maintaining a Large Variance of Membrane Fluctuations

Our experimental observations and model simulations revealed that combined LTP and LTD modulates response threshold to auditory nerve inputs. However, we have also observed that threshold reduction is associated with minimal gain changes, where gain is defined as the slope of the response function about threshold (Figs. 6A, 5D1 for experimental measurements and Fig. 5B2 for model simulations). Is threshold modulation with minimal gain changes mediated specifically by combined LTP and LTD or is it a common feature of input-output function modifications induced by other known modulatory mechanisms? To answer this question, we took advantage of the model and tested the effect of a change of the firing rate of modulatory inputs, another strategy known to modulate neuronal processing (Koch, 1999; Chance et al., 2002). The effects of changes in the firing rate of modulatory inputs on threshold and gain have been previously described (Chance et al., 2002), and will be used for comparison purposes to highlight the novelty of our mechanism (Fig. 6 and 7). Previous studies have provided experimental evidence that changes in the rate of modulatory inputs affect gain, threshold and input resistance (Chance et al., 2002). While our definition of neural response gain is different from these studies (we consider response probability to a transient input while Chance et al., 2002 consider firing rate measured over longer time scales), our model predictions are based on our definition of gain and are in agreement with previous studies. The effects of parallel fiber rate changes have already been validated experimentally, and thus experimental validation will not be provided for this part of our modelling findings.

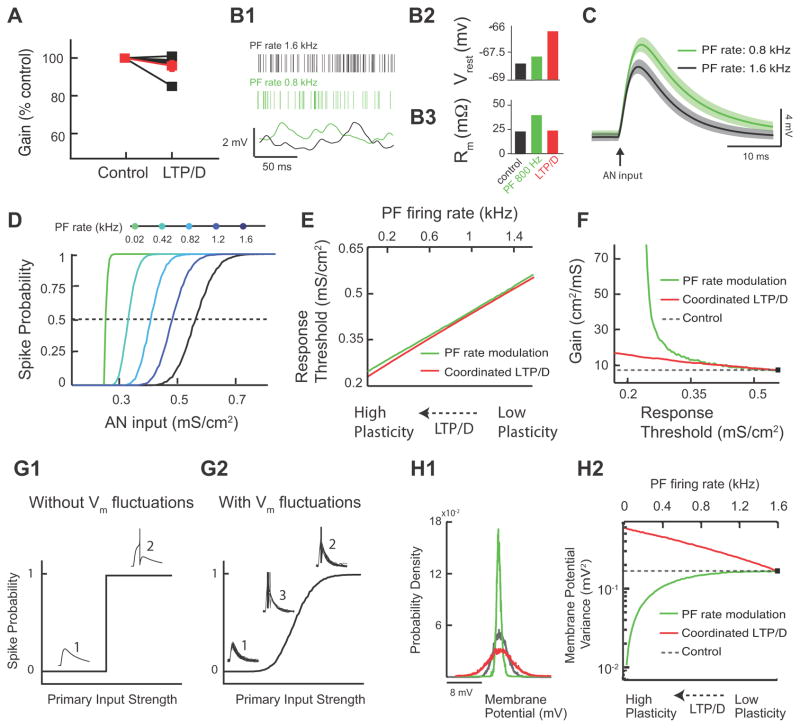
Fig. 6. Combined LTP and LTD Changes Threshold Response with Minimal Gain Changes, while Parallel Fiber Rate Modulation Causes Significant Gain Changes.

(Panel A illustrates experimental data, while the rest of Fig 6 illustrates modelling data). A. Measurement of gain in control and after combined LTP and LTD for 5 different fusiform cells (values were normalized to control: control: 100%; combined LTP and LTD: 95.8% ± 2.8% of control, p>0.05, the red trace represents the average response). Gain represents the slope of the response function around threshold. The slope was derived from experiments illustrated in 5D1, D2. B1. Fusiform cell model membrane potential (V_rest) (bottom) for different PF rates (top: control PF rate in black vs. lower PF rate in green). B2. Average resting model membrane potential (V_rest) for control (black) vs. lower PF rate (green). For comparison purposes combined LTP and LTD value is shown in red (same as in Fig. 4C1) B3. Average model input resistance R_m for the same conditions as (B2). For comparison purposes combined LTP and LTD values shown in red (same as in Fig. 4C2). C. Average model membrane response to an AN input in control (black trace) vs. PF rate modulation (green trace). Shaded areas are ± one standard deviation. D. Model fusiform cell response probability as a function of AN input strength (g_AN) for different PF rates. E. The range of PF rates (top axis, green curve) that gave equivalent threshold shifts to the threshold shifts observed for the range of combined LTP and LTD modulation shown in Fig. 5B2 (bottom axis, red curve). F. Gain plotted as a function of threshold for combined LTP and LTD (red) and PF rate (green) modulation (dashed line indicates control values). G1. Schematic representation of input-output functions in the absence of membrane potential fluctuations. Weak synaptic primary inputs never reach spiking threshold (1), while strong inputs always elicit a spike (2). G2. Schematic representation of input-output function in the presence of membrane potential fluctuations. There is a graded response with increasing primary input strength. Note the emergence of a third response state (3) where spiking occurs with a probability between 0 and 1. H1. Membrane potential probability density function for control (black), for PF firing rate reduction (green) and for combined LTP and LTD (red). For comparison purposes the density functions were shifted so that they have identical mean values. H2. The variance of membrane potential fluctuations as a function of combined LTP and LTD (bottom axis, red curve) and PF rate modulation (top axis, green curve). The dashed line indicates control values. The range of combined LTP and LTD, and PF rate modulation are identical to that shown in E.

Fig. 7. Combined LTP and LTD Modulates Response Threshold with Minimal Effect on First Spike Latency, while Parallel Fiber Rate Modulation Causes Significant Latency Modulation.

(Panel D illustrates experimental data, while the rest of Fig 7 illustrates modelling data) A1. First spike latency is defined as the time interval between auditory nerve pulse onset (bottom) and fusiform cell spike response (top). All model simulations have auditory nerve input strengths set at threshold (top: 50% of inputs elicit spike responses). A2. Model first spike latency probability density (50,000 realizations). All model parameters are at control values (Fig. 5B1). B1. First spike latency probability density as combined LTP and LTD is recruited. Colours as in Fig. 5B1. B2. Model first spike latency probability density as parallel fiber firing rate is reduced. Colours as in Fig. 6D. C. Mean first spike latency plotted as a function of threshold for combined LTP and LTD (red) and PF rate (green) modulation. Parameter ranges are identical to those of Fig. 6E, F. D. (Panel D illustrates experimental data). Measurement of spike latency in control and after combined LTP and LTD for 5 different fusiform cells (values were normalized to control: control: 100%; combined LTP and LTD: 99.8% ± 2. % of control p>0.05, the red trace represents the average response). Latency was calculated from experiments illustrated in 4D1, D2. E1. Model passive membrane potential timescale as combined LTP and LTD is recruited. Colours match panel B1. E2. Model passive membrane potential timescale as parallel fiber firing rate is reduced. Colours match panel B2. F1. Example membrane potential realizations (20) for low (red) and high (yellow) combined LTP and LTD (top). For reference the auditory nerve input for both cases is shown (below). Colours match panel B1. F2. Example model membrane potential realizations (20) for high (blue) and low (green) parallel fiber rates (top). For reference the auditory nerve input for both cases is shown (bottom). Colours match panel B2.

We studied the effect of changes in parallel fiber firing rate on fusiform cell response, while keeping synaptic strengths fixed (Fig. 6B1). Reduction in parallel fiber firing rate caused a balanced reduction in parallel fiber EPSCs and disynaptic IPSCs, as parallel fibers provide excitatory input to both principal neurons and interneurons. For a passive, point neuron model (simplified model) the mean resting membrane potential is proportional to (g_e−g_i)ν, where g_e is the excitatory strength, g_i is inhibitory strength and ν is the parallel fiber firing rate (Doiron et al., 2001; Chance et al., 2002). While this simplified model ignores the shunting component between excitatory and inhibitory components, we use it here for its pedagogic value. However, all our findings are tested in our two-compartment model and for different degrees of somato-dendritic coupling. Reduction in parallel fiber firing rate modulation where excitation and inhibition are balanced (g_e−g_i≈0) caused no changes in the resting membrane potential in our two-compartment model (Fig. 6B2). This finding is consistent with our expectations from our simplified model. Nonetheless, the decrease in parallel fiber firing rate reduced synaptic conductance and thus increased the total membrane resistance (Fig. 6B3). Thus, the simulated fusiform cell membrane potential depolarization to a brief auditory nerve synaptic input was multiplicatively scaled upon reduction of parallel fiber firing rate (Fig. 6C black vs. green). This multiplicative effect is based on a simple application of Ohm’s law (V=IR), since membrane resistance increases with decreased PF firing rate. Multiplicative scaling of the auditory nerve EPSP is expected to reduce the threshold for firing in response to auditory nerve inputs. Indeed, similar to the effects of combined LTP and LTD strategy, reducing parallel fiber firing rates brought the membrane potential response to auditory nerve inputs closer to spike threshold and thus decreased the response threshold to auditory nerve inputs (Fig. 6D).

While both modulatory strategies (combined LTP and LTD vs. parallel fiber firing rate modulation) are equally effective in reducing the response threshold to auditory nerve inputs, they achieve this computational task through different mechanisms. To determine whether these two different mechanisms affect gain of input-output functions in a similar or differential manner, we compared threshold and gain changes induced by the two different modulatory strategies. To facilitate this comparison, we computed the range of parallel fiber firing rates that produced equivalent threshold modulations to that of combined LTP and LTD (Fig. 6E). Despite the identical effect of these two strategies on response threshold, parallel fiber firing rate modulation increased gain to a much larger extent compared to gain changes produced by combined LTP and LTD (Fig. 6F). Therefore, combined LTP and LTD provides mechanistic specificity in enabling changes in threshold while maintaining gain, relatively, fixed. This finding illustrates that while combined LTP and LTD of modulatory inputs allows for an adaptive sensory input detection threshold (threshold modulation), at the same time, by maintaining gain it also ensures that the same distribution of inputs can be encoded at different thresholds. This is a distinct computational advantage that requires specialized biophysical mechanisms that can decouple threshold from gain modulations.

To investigate the specific mechanism via which combined LTP and LTD provides homeostatic regulation of gain, we used our model to compare the effect of combined LTP and LTD and of parallel fiber firing rate modulation on synaptic noise generated by parallel fiber inputs. Previous studies have established that the amount of fluctuating synaptic activity (noise) determines, in large part, the gain of input-output functions (Ho and Destexhe, 2000; Doiron et al., 2001; Chance et al., 2002; Mitchell and Silver, 2003; Prescott and De Koninck, 2003; Mehaffey et al., 2005; Cardin et al., 2008, but see Rothman, 2009 #617). In response to transient inputs and without synaptic noise, input-output relationships are step functions with infinite gain at threshold (Fig. 6G1). Synaptic noise causes voltage fluctuations that smooth the discontinuity between subthreshold and suprathreshold EPSPs, and thus reduce overall gain (Fig. 6G2). Therefore, any manipulation that affects the fluctuations of the membrane potential is expected to affect gain. Given the importance of membrane potential fluctuations in determining the gain of input-output functions, one hypothesis would predict that combined LTP and LTD provides homeostatic regulation of the variance of membrane fluctuations and thus leads to minimal changes in gain. Additionally, significant gain changes observed with parallel fiber firing rate modulation are expected to be associated with significant changes in the variance of membrane fluctuations.

To test these hypotheses we computed the changes in the variance of membrane fluctuations for the two modulatory strategies. For a passive, point neuron model, the variance of membrane potential fluctuations (σ²) is proportional to (g_e²+g_i²)ν (Doiron et al., 2001; Chance et al., 2002). In our two compartment model, for parallel fiber firing rate modulation, the variance of membrane potential fluctuations becomes dramatically smaller with decreasing parallel fiber rates; (g_e²+g_i²)ν gets smaller as ν decreases (compare black vs. green width of distributions shown in Fig. 6H1, and see also Fig. 6H2 green). On the other hand, combined LTP and LTD increases the variance of excitatory inputs (g_e²ν gets larger with increasing g_e due to LTP) and decreases the variance of inhibitory inputs (g_i²ν gets smaller with decreasing g_i due to LTD), thus ensuring that the total membrane potential variance does not approach low values (compare black vs. red width of distribution in 6H1, and see also Fig. 6H2 red). Such homeostatic control of membrane potential variance maintains gain relatively unchanged. While it is well known how changes in the mean and variance of a modulatory input control response threshold and gain, the presence of nonlinear mechanisms and stochastic fluctuations in most cases lead to mixed additive (threshold) and multiplicative (gain) shifts (Silver, 2010). Threshold modulation without gain changes has been associated with tonic inhibition in the absence of membrane potential fluctuations (Semyanov et al., 2004) or with outwardly rectifying tonic GABA inhibition in the presence of membrane potential fluctuations (Pavlov et al., 2009). However, in these cases inhibition does not contribute to membrane potential fluctuations, necessitating an additional source of membrane potential fluctuations. Taken together, our results indicate that combined LTP and LTD provides threshold modulation and homeostatic regulation of gain with a single modulatory path.

Combined LTP and LTD Preserves Spike Latency by Maintaining a Low Membrane Time Constant

Spike probability and response gain are important features of most neural codes (Silver); however, dynamic sensory signals also require precise spike timing for accurate representations of temporally precise stimuli (Kayser et al.; Grothe and Klump, 2000; VanRullen et al., 2005; Tiesinga et al., 2008; Yang et al., 2008). Thus, we next focused on the impact of combined LTP and LTD on the temporal processing of auditory nerve inputs by fusiform cells. When input strength was adjusted to drive fusiform cell responses at threshold, we measured the latency between the model auditory nerve stimulation and the fusiform cell first spike response (Fig. 7A1). The level of membrane potential fluctuations during physiological (in vivo) conditions remains unknown. However, in vivo experiments have determined the first spike latency distribution for fusiform cells (Joris and Smith, 1998). The trial-to-trial variability in spike latency is largely dependent on the magnitude of membrane potential fluctuations, and hence the spread of latency provides a marker for the levels of membrane potential fluctuations. The magnitude of membrane potential fluctuations in our model was chosen to match the spread of latencies reported by in vivo studies (Fig. 7A2). When threshold was shifted with combined LTP and LTD (Fig. 5B2) a near identical first spike latency density occurred over a broad range of LTP/LTD (Fig. 7B1). In contrast, when equivalent threshold shifts were induced via a reduction in parallel fiber firing rate (Fig. 6D), the density of first spike latencies shifted to significantly longer latencies (Fig. 7B2). These results were robust and revealed that minimal mean response latency shifts were recruited by combined LTP and LTD (Fig. 7C, red). In contrast, significant mean latency modulation was associated with parallel fiber firing rate modulation that produced equivalent threshold modulations to that of combined LTP and LTD (Fig. 7C, green).

To test experimentally the predicted insensitivity of mean latency to combined LTP and LTD, we simulated parallel fiber synaptic activity by injecting a train of subthreshold PSCs into a fusiform cell (as in Fig. 4D1–D3), while we simultaneously stimulated the deep layer of the DCN (as in Fig. 5C, left) to evoke auditory nerve-mediated EPSPs and spike responses (as in Fig. 5C right). Spike latency to an auditory nerve input was measured and revealed no significant changes before and after combined LTP and LTD (Fig. 7D), despite large shifts in threshold response (Fig. 5D1, D2). Thus, both our computational and experimental data indicates that combined LTP and LTD preserves the response latency of auditory nerve inputs under a broad range of threshold shifts.

The fixed latency density with combined LTP and LTD is a surprising and important result, as plastic changes in the amount of synaptic input to a neuron, often change neuronal input resistance and membrane time constant (Silver; Chance et al., 2002; Cardin et al., 2008; Ly and Doiron, 2009), and thus are expected to also change spike latency. However, the specific conductance changes during combined LTP and LTD (Fig. 5B1) are such that the model membrane time constant remains roughly fixed (Fig. 7E1). This is in contrast to the increase in membrane time constant associated with a reduction of parallel fiber firing rate (Fig. 7E2). This distinction between modulation schemes is easily understood for passive, point neuron models, since the membrane time constant is inversely proportional to (g_e+g_i)ν. During combined LTP and LTD the increase in g_e with simultaneous decrease in g_i keeps (g_e+g_i)ν at a relatively high value, maintaining membrane time constant at a low value. Thus, despite the reduction of response threshold during combined LTP and LTD (Fig. 7F1, bottom, compare red and yellow traces), the membrane integration remains roughly fixed (Fig. 7F1, top) and spike threshold crossing occurs at comparable latencies for the drastically different thresholds (Fig. 7F1, top). In contrast, a reduction in parallel fiber rate (ν) reduces significantly (g_e+g_i)ν, and thus increases the membrane time constant. This increase leads to slower membrane integration at low thresholds (Fig. 7F2, top, compare blue and green traces), resulting in longer first spike latency (Fig. 7F2, top). A reduction in parallel fiber rate will also result in a reduction of membrane potential fluctuations, thus providing an additional mechanism for increased first spike latency during low parallel fiber firing rates.

Identification of cellular mechanisms allowing dissociation of firing rate modulation from temporal code modulation is a novel finding. Rate and timing modulations involve a change in the synaptic inputs from a modulatory pathway, and hence are expected to co-vary with one another. Combined LTP and LTD navigates the intertwining of rate and timing modulation, so as to allow decoupled modulations for threshold and latency. Such dissociation may allow sensory systems to adapt their firing rate and yet maintain a faithful encoding of the fine temporal structure of sensory inputs, which is necessary for accurate stimulus identification and discrimination.

Combined LTP and LTD is a Robust and an Efficient Synaptic Plasticity Pathway for Threshold Modulation and Homeostatic Control of Gainand Spike Latency

Thus far, we have examined the effect of combined LTP and LTD on threshold modulation with homeostatic control of response gain and first spike latency for specific parameters (Figs. 5–7). While membrane resistance, spike threshold, resting membrane potential and synaptic parameters (including the amount of LTP and LTD) matched the experimentally measured values, the somatodendritic coupling constant (g_c) and the parallel fiber firing rate are not currently known. The validity of our conclusions about the role of combined LTP and LTD on auditory nerve input processing are robust over a wide range of g_c and parallel fiber firing rates. Auditory nerve response modulation by combined LTP and LTD for g_c values ranging from 0.005 mS/cm² to 0.2 mS/cm² shows near equivalent shifts in gain (Fig. 8A, red-yellow curves) and mean spike latency (Fig. 8B, red-yellow curves) as threshold was modulated. These shifts were minor when compared to the shifts observed when synaptic strength was fixed (no synaptic plasticity allowed) and firing rate modulation approach was used (Fig. 8A,B, green curves: 8A same curve as in 6F and 8B same curve as in 7C). In addition, auditory nerve response modulation by combined LTP and LTD for parallel fiber rates ranging from 0.75 kHz to 3 KHz showed similar gain (Fig. 8C, red-yellow curves) and latency (Fig. 8D, red-yellow curves) shifts as threshold was modulated. These shifts were smaller than the observed shifts when synaptic strength was fixed (no synaptic plasticity allowed) and firing rate modulation approach was used (Fig. 8C,D, green curves: 8C same curve as in 6F and 8D same curve as in 7C). Together, our results indicate that combined LTP and LTD modulates threshold with homeostatic regulation of gain and first spike latency (Figs. 4–6) for a wide range of parameters.

Fig. 8. Combined LTP and LTD Provides a Robust Mechanism for Threshold Modulation with Homeostatic Control of Gain and Latency.

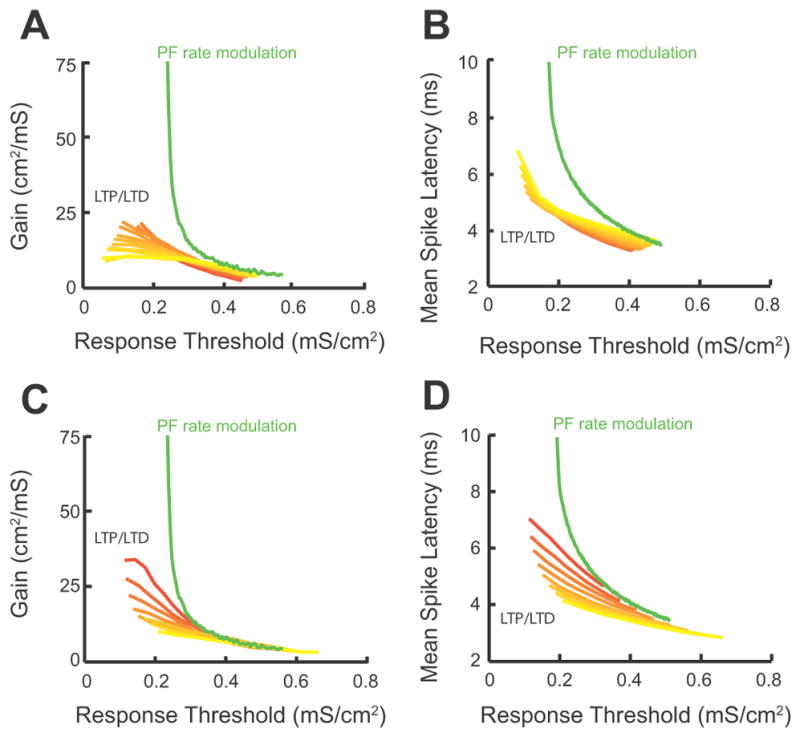
(Fig 8 illustrates modelling data) A. Response gain as a function of threshold during combined LTP and LTD for values of electrotonic coupling between the somatic and dendritic compartment (g_c) ranging from 0.005mS/cm² (yellow curve) to 0.2mS/cm² (red curve). Each curve is computed as LTP/LTD follows the path used throughout the study (Fig. 5B1). For comparison purposes the gain/threshold curve for a different modulatory mechanism that does not involve combined LTP and LTD is shown in green (parallel fiber rate modulatory mechanism; replotted from Fig. 6F; g_c=0.1 mS/cm² for the green curve). B. Mean spike latency as a function of threshold during combined LTP and LTD for the same values of g_c as used in panel A. For comparison purposes the mean spike latency/threshold curve for the parallel fiber rate modulatory mechanism is shown in green (replotted from Fig. 7C). C. Response gain as a function of threshold during combined LTP and LTD for values of parallel fiber firing rates ranging from 0.75kHz (red curve) to 3kHz (yellow curve). For comparison purposes the gain/threshold curve for a different modulatory mechanism that does not involve combined LTP and LTD is shown in green (parallel fiber rate modulatory mechanism; replotted from Fig. 6F). D. Mean spike latency as a function of threshold during coordinated LTP and LTD for the same values of parallel fiber rates as used in panel C. For comparison purposes the mean spike latency/threshold curve for the parallel fiber rate modulatory mechanism is shown in green (replotted from Fig. 7C).

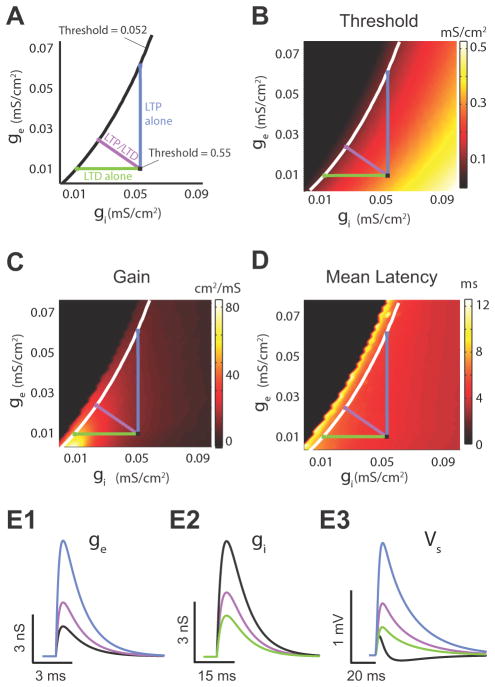
While combined LTP and LTD supports threshold modulation, with homeostatic regulation of gain and latency, it is not clear whether any other synaptic plasticity modulation is capable of producing similar results. To answer this question, we used our model to compute threshold, gain, and latency for a broad range of excitatory and inhibitory conductance strength (g_e, g_i), corresponding to various levels of LTP or LTD of EPSPs and/or IPSPs. More specifically, we compared threshold, gain and latency modulation obtained with combined LTP and LTD (Fig. 9A purple line) to that obtained with LTP (Fig. 9A black line) or LTD alone (Fig. 9A, green line). In our comparisons, all modulatory schemes shared the same control point (Fig. 9A black square) and followed distinct paths leading to identical changes in threshold magnitude (Fig. 9A black “isothreshold” line). LTP of excitation decreased the response threshold with a limited change in gain, and latency similar to the modulation caused by combined LTP and LTD (Fig. 9B–D; compare the control – black square, to both the LTP – blue square and combined LTP and LTD – purple square). However, the requisite amount of LTP required for an equivalent threshold shift was excessive (~ 400 – 500 % of control, Fig. 9D); compare the magnitude of the black vs. the magnitude of the blue trace), and therefore non-physiological. This result is also supported by our experimental findings, showing that synaptically induced LTP was not sufficient to enlarge the integration window (Fig. 3F), but instead changes in integration window required combined LTP and LTD (Fig. 3E2, F). In contrast, moderate levels of LTD caused significant threshold changes (Fig. 9B). However this threshold change was associated with significant gain and latency changes (Fig. 9C, D; compare the control – black square, to both the LTD – green square and LTP/LTD – purple square). Finally, “combined LTP” (LTP of excitatory synapses and LTP of inhibitory synapses) or “combined LTD” (LTD of excitatory synapses and LTD of inhibitory synapses) do not change response threshold, while they change gain and latency (Fig. 9B–D). Taken together, combined LTP and LTD provides a robust and efficient synaptic plasticity “path” that shifts threshold and still provides homeostatic control of gain and latency.

Fig. 9. Combined LTP and LTD Is an Efficient Synaptic Plasticity Path for Threshold Modulation with Homeostatic Control of Gain and Latency.

(Fig 9 illustrates modelling data) A. Three different plasticity paths transitioning from a high threshold (0.55 mS/cm²) to a low threshold value (0.052 mS/cm²). The purple line represents the combined LTP and LTD path; the blue line represents LTP path of excitatory inputs; the green line represents LTD of inhibitory inputs. B. Response threshold (colour) computed over a range of different excitatory and inhibitory conductance values (g_e/g_i). The white curve is the “iso-threshold” curve for a constant threshold of 0.052 mS/cm². C. Same as B except for gain. D. Same as B except for mean latency. (E1) Excitatory conductance (E2) inhibitory conductance, and (E3) the membrane response for the control condition (black), combined LTP and LTD (purple), LTP (blue), and LTD (green) paths that yielded identical changes in threshold. Parameters are given by the coloured squares in A.

Discussion

Our study unmasks a novel circuit mechanism that enables threshold modulation while keeping response gain and latency approximately invariant. Specifically, combined LTP and LTD of parallel ber inputs shifts the balance of excitation and inhibition in DCN principal neurons. This shift produces an enlarged integration window over which parallel ber inputs summate to reach threshold. The broader integration window allows for increased temporal summation of modulatory inputs, depolarizes the principal neuron, and reduces the response threshold to auditory nerve inputs. However, combined LTP and LTD minimally changes membrane voltage fluctuations and membrane time constant, effectively fixing the gain and response latency to brief, transient inputs. Hence, combined LTP and LTD of modulatory pathway gates information transfer of sensory inputs while providing homeostatic regulation of response sensitivity and response timing, a distinct advantage in the dynamic processing of sensory inputs.

Modulation of input-output functions by long-term synaptic plasticity

Previous studies have explored the influence of synaptic plasticity of feedforward (primary) signals on threshold and gain of neuronal response to the same feedforward signals (Frick et al., 2004; Marder and Buonomano, 2004; Campanac and Debanne, 2008; Carvalho and Buonomano, 2009). Our study differs in three fundamental ways from previous studies. We reveal a novel plasticity rule via which synaptic plasticity of a modulatory pathway determines the response threshold of the principal neuron to its fixed, primary inputs. Previous studies in the cerebellum and cerebellar-like structures have examined the interaction of primary signals (climbing fiber for cerebellum and afferent input from sensory surface for cerebellum-like structures) and modulatory signals (parallel fibers for both cases) in inducing synaptic plasticity (LTD) in the feedback pathway (Harvey-Girard et al.; Bell et al., 1997; Ito, 2001; Tzounopoulos et al., 2004). Similarly, several recent studies in the hippocampus have reported that interaction between perforant path and Schaffer collaterals results in a variety of cellular or network phenomena that include modi cations in synaptic plasticity, enhanced forward propagation of distal dendritic Na⁺ spikes, and alterations in inhibitory input and dendritic plateau potentials (Remondes and Schuman, 2002; Ang et al., 2005; Jarsky et al., 2005; Dudman et al., 2007; Takahashi and Magee, 2009).

The mechanisms via which combined synaptic plasticity of the parallel fiber circuit changes threshold and gain in response to direct auditory nerve inputs is novel and fundamentally different from plasticity mechanisms that change gain and threshold in feedforward pathways (Carvalho and Buonomano, 2009). In this latter case, the modulation occurs in the primary (feedforward) input and involves changes in the peak, slope and width of the compound PSP (Carvalho and Buonomano, 2009). Changes in the width of the compound PSP are expected to change spike timing (Pouille and Scanziani, 2001), thus changing temporal fidelity of modulated inputs. In contrast, the mechanism that we reveal here relies on a depolarization of resting membrane potential upon which a fixed primary input is processed. Therefore, our mechanism does not affect the properties of the EPSP of the auditory input, and thus is expected to preserve the spike timing of responses elicited by auditory nerve inputs.

Excitatory and inhibitory synaptic plasticity in the DCN differs from previous studies in hippocampal (Lamsa et al., 2005; Carvalho and Buonomano, 2009), cortical (Froemke et al., 2007) and cerebellar circuits (Mittmann and Hausser, 2007) in which similar signs of plasticity in excitatory and inhibitory inputs are reported. These studies have supported the idea that long-term synaptic plasticity that produces balanced changes in excitatory and inhibitory inputs (combined LTP or combined LTD of excitatory and inhibitory synapses) is necessary for maintaining invariant integration windows and in creating changes in neuronal gain but not in threshold (Lamsa et al., 2005; Carvalho and Buonomano, 2009). However, our results suggest that activity-dependent modulation of integration windows may provide a cellular mechanism that allows sensory systems to adapt to different patterns of sensory activity.

Threshold vs. Gain Modulations

The input-output function of a neuron is sensitive to the characteristics of its ambient, or background, synaptic activity (Destexhe et al., 2003). In agreement with previous studies, we find that modulations of synaptic activity that affect membrane potential fluctuations change the gain of input-output functions (Ho and Destexhe, 2000; Doiron et al., 2001; Chance et al., 2002; Mitchell and Silver, 2003; Prescott and De Koninck, 2003; Cardin et al., 2008). Modulation of excitation and inhibition affects the input resistance and membrane potential variance, and thus shifts both the threshold and gain of input-output functions (Chance et al., 2002; Cardin et al., 2008). When changes in excitation balance those of inhibition it is possible to observe a multiplicative scaling of response gain without a shift in response threshold (Chance et al., 2002). Other theoretical schemes that could break the balance of excitation and inhibition, such as having parallel fibers drive some cartwheel cells and fusiform cells independently, could provide the same gain and threshold modulation. However, this scheme requires that the granule cells that contact cartwheel cells decrease their firing, while at the same time the granule cells that contact the fusiform cell increase their firing. Although such an architectural and physiological arrangement could cause similar gain and threshold modulations, there is not any physiological evidence that supports this arrangement. Taken together, combined LTP and LTD is physiologically relevant in the DCN and it expands existing modulatory schemes, offering the capacity to shift threshold independently of gain.

What is the advantage of shifting threshold with minimal changes in gain? Threshold changes redefine the boundary between weak and strong stimuli, and maintaining gain during a threshold change ensures that the same distribution of inputs can be encoded at different thresholds. Threshold modulation without gain adjustment has been observed in orbitofrontal cortex in response to shifting mean reward level (Tremblay and Schultz, 1999) and in visual cortex during different levels of subject attention to small field visual stimuli (Reynolds and Heeger, 2009). In a complementary fashion, gain modulation with a fixed threshold occurs in response to changes in reward variability (Kobayashi et al.), and during different levels of subject attention to large field visual stimuli (Reynolds and Heeger, 2009). In total, threshold and gain modulations serve distinct and separable neural computations that are associated with specific changes in input statistics or task parameters. This functional separation requires distinct cellular mechanisms for threshold and gain modulation. We reveal one such mechanism, wherein combined LTP and LTD modulates threshold with minimal gain changes.

Threshold vs. Latency Modulations

Sensory signals are coded by multiple aspects of spike trains, including spike rate, first spike latency (latency code), ongoing spike timing (interspike interval), and phase firing (Panzeri et al.; Grothe and Klump, 2000; VanRullen et al., 2005; Tiesinga et al., 2008). In many sensory nuclei the latency between the stimulus onset and the first spike response carries critical stimulus information (Panzeri et al., 2001; Chase and Young, 2008; Gollisch and Meister, 2008). Our plasticity-mediated threshold modulation could be used to align spike response threshold to specific stimulus intensities. Latency code invariance to threshold changes permits any latency decoder to be well tuned for a range of stimulus intensities, offering a simple solution to dissociate rate from temporal decoding schemes. We expect that similar mechanisms for homeostatic control of temporal coding exist in brain regions where temporally sensitive inputs span a large range of intensity.

The DCN is important for processing of spectral localization cues (Oertel and Young, 2004). These cues involve modifications in the spectra that are produced when sound interacts with the external ear, or pinna, and are necessary for sound localization in the vertical plane (Oertel and Young, 2004; Tzounopoulos and Kraus, 2009. DCN principal neurons, fusiform cells, whose axons convey signals from the DCN to the inferior colliculus, provide the representation of these acoustic cues (Oertel and Young, 2004). While first spike latency has not been explored as an important feature of the DCN code, inferior collicular neurons (the target of DCN neurons) use first spike latency to encode information about spectral notches {Chase, 2008 #619), suggesting that a latency code may exist in fusiform cells. Although, inferior colliculus cells receive inputs from other neurons of the superior olivary nuclei and of the lemniscal nuclei that are known to encode acoustic information in the timing of firing, it is the fusiform cell input that is encoding cues for spectral localization. Future in vivo studies are needed to provide a direct link between the mechanism proposed here and the existence of a latency code in fusiform cells.

In summary, previous studies have established that neural circuits use homeostatic plasticity to maintain stable firing rate (Turrigiano, 2008). We suggest that homeostatic control of gain and latency during modulation of threshold is another general feature of neural circuit design employed by networks performing tasks that require adaptive threshold and unchanged neuronal responsiveness and invariant temporal code.