Abstract
Human decision-making involving independent events is often biased and affected by prior outcomes. Using a controlled task that allows us to manipulate prior outcomes, the present study examined the effect of prior outcomes on subsequent decisions in a group of young adults. We found that participants were more risk-seeking after losing a gamble (Riskloss) than after winning a gamble (Riskwin), a pattern resembling the gambler’s fallacy. Functional MRI data revealed that decisions after Riskloss were associated with increased activation in the frontoparietal network, but decreased activation in the caudate and ventral striatum. The increased risk-seeking behavior after a loss showed a trend of positive correlation with activation in the frontoparietal network and the left lateral orbitofrontal cortex but a trend of negative correlation with activation in the amgydala and caudate. In addition, there was a trend of positive correlation between feedback-related activation in the left lateral frontal cortex and subsequent increased risk-seeking behavior. These results suggest that a strong cognitive control mechanism but a weak affective decision-making and reinforcement learning mechanism that usually contribute to flexible, goal-directed decisions can lead to decision biases involving random events. This has significant implications for our understanding of the gambler’s fallacy and human decision making under risk.
Keywords: Amygdala, Decision Making, Emotion, Frontal Cortex, functional MRI, Gambler’s Fallacy, Orbitofrontal Cortex, Reinforcement Learning, Striatum
Introduction
A fundamental issue in decision neuroscience is how risky decision making varies as a function of prior outcomes. A greater tendency to make a risky choice following a loss than following a gain underlies some important phenomena such as the gambler’s fallacy. First described by Laplace (Laplace 1820), the gambler’s fallacy is the mistaken propensity to perceive independent events as negatively dependent, such that the next independent outcome should be different from the previous ones. The gambler’s fallacy has been revealed in many daily-life decisions, such as stock market trading (Odean 1998) and gambling (Croson and Sundali 2005). Furthermore, the gambler’s fallacy may contribute to certain clinical phenomena such as pathological gambling, which could explain why a gambler persists in gambling in the face of mounting losses, believing that their “luck” would change after a streak of losses (Sharpe and Tarrier 1993).
In this study we used neuroimaging techniques in conjunction with a controlled risky decision making task to simulate the behavioral and neurological reactions to wins and losses in the gambler’s fallacy. Studies of patients with brain lesions have suggested that impaired mechanisms of affective decision-making are responsible for the types of risky behaviors underlying the gambler’s fallacy. Specifically, Shiv and colleagues have shown that in an investment game, where gains and losses were determined by a coin toss, healthy controls and brain-damaged control patients (i.e., patients with brain damage outside the ventromedial prefrontal cortex) showed a tendency to quit after losses. In contrast, patients with brain lesions that included the mesial orbitofrontal cortex (OFC)/ventromedial prefrontal cortex (and also patients with damage to other components of the neural circuitry that is critical for processing emotions, such as the insular cortex and amygdala), showed persistence and an increase in risky behavior after a series of losses (Shiv, et al. 2005).
Similarly, in the Iowa gambling task (IGT) that simulates daily-life decision-making (Bechara, et al. 1994), healthy participants gradually shift to advantageous decks by (implicitly) developing predictive somatic responses to disadvantageous decks, whereas patients with focal brain damages in the ventromedial PFC are impaired in this affective decision capacity, and keep choosing the disadvantageous decks after severe losses (Bechara, et al. 2003; Bechara, et al. 1999; Bechara, et al. 2000b; Bechara, et al. 1995; Bechara, et al. 1996). More specifically, when these patients are asked to declare what they know about what is going on in the IGT, most of them demonstrate a conceptual knowledge of the contingencies, and they know which ones are the bad decks (Bechara, et al. 1997). Yet when they are asked to choose again from the different decks, most often these patients return to the disadvantageous decks (Bechara, et al. 1997). When the patients were confronted with the question: “Why are you selecting the decks that you have just told me were bad decks?” the most frequent answer has been “I thought that my luck is going to change.” (Unpublished clinical observations). Together, the many pieces of evidence, combined with the clinical observations, suggest that phenomena related to the gambler’s fallacy seem most prominent in cases where there is evidence of impaired affective decision making involving the mesial OFC/ventromedial prefrontal cortex, and the amygdala.
Psychological studies of the gambler’s fallacy have primarily viewed it as a cognitive bias produced by a psychological heuristic called the representativeness heuristic. According to this heuristic, people believe short sequences of random events should be representative of longer ones (i.e., law of small numbers) (Rabin 2002). Others argue that the gambler’s fallacy might stem from the tendency to take a gestalt approach to understand independent events (Roney and Trick 2003). The latter view echoes the neuroimaging data that show that the human prefrontal cortex is capable of perceiving patterns in random series, even when these patterns do not actually exist (Huettel, et al. 2002; Ivry and Knight 2002).
The present functional imaging study aimed at testing the hypothesis that the gambler’s fallacy is associated with weak activations in the affective decision making system, and ensuing strong activations in the lateral prefrontal areas, which are more involved in cognitive control. To test these hypotheses, we employed functional magnetic resonance imaging (fMRI) and a simple gambling task to examine how prior outcomes (gain vs. loss) affect subsequent risky decisions and the underlying neural mechanisms.
Materials and Methods
Subjects
Fourteen healthy adults participated in this study (7 males and 7 females, mean = 23.8 years of age, ranging from 22 to 29). All subjects had normal or corrected-to-normal vision. They were free of neurological or psychiatric history and gave informed consent to the experimental procedure, which was approved by the University of Southern California Institutional Review Board.
The Modified Cups Task
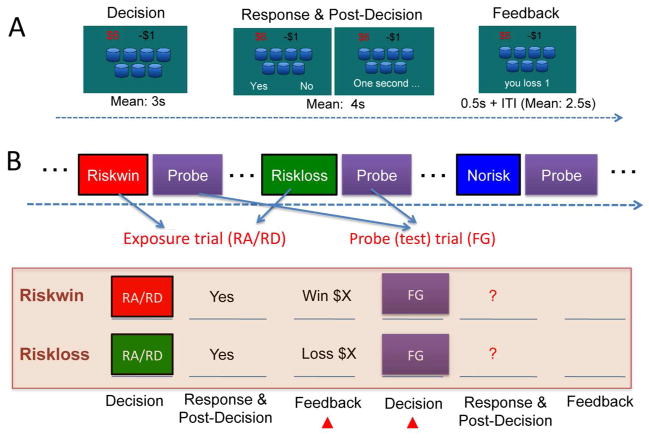
Figure 1A depicts the Modified Cups Task (Levin, et al. 2007) and the experimental design. In each gamble, a number of cups (ranging from 3 to 11) were presented on the computer screen, with the first cup containing a large gain (ranging from $4 to $8) and all the rest containing a small loss (−$1). The probability (as determined by the number of cups) and magnitude of the gain were independently manipulated such that some combinations create fair gambles (FG), that is, the expected value (EV) of the gamble equals zero (e.g., $5 gain in one cup and $1 loss in the other five cups). Some combinations are slightly risk-advantageous (RA), meaning that the EV is larger than zero (e.g., $5 gain in one cup and $1 loss in the other three cups). Some combinations are slightly risk-disadvantageous (RD), meaning that the EV is smaller than zero (e.g., $5 gain in one cup and $1 loss in the other six cups). Participants were simply asked to play a series of gambles. For each gamble, they could choose to gamble or not to gamble. If they took a gamble, the computer would randomly choose one cup and determine whether they won or lost (see an exception below, which was unknown to the subjects). If they chose to pass on a gamble, they would win or lose nothing.
Fig. 1.
The (A) structure of the Modified Cup Task and (B) the experimental design. In each gamble, a number of cups were presented with the first one containing a large gain and all the others containing a small loss. At the Decision stage, participants were shown the gamble and were asked to contemplate the gamble and make a decision of whether or not to take the gamble, without indicating any button response. After a varied period of delay, the response cue (“Yes” and “No” on each side) was shown on the screen and participants were asked to indicate a button press. After the response, a 0.5s feedback was presented after some delay to inform participants of the outcome. The next trial would begin after a jittered delay. Depending on the combination of the reward amplitude and probability (determined by the number of cups), the gamble could be a fair gamble (FG), risk advantageous (RA) or risk disadvantageous (RD) (See Methods). The RA and RD trials were used as the exposure trials, each followed by a FG trial serving as the probe trial to examine the effect of prior outcome on subsequent decisions. The present study thus focused on the Riskwin and Riskloss trials and the probe trials that followed them.
The Experimental Conditions and Design
The primary goal of this study was to examine whether winning or losing a gamble would change participants’ subsequent risky decisions. Rather than arranging the trials randomly and then categorizing them post hoc based on participants’ choices and outcomes, the present study used a different approach to enable better control of the prior outcomes, and to minimize the requirement for post hoc matching. In order to do this, we included two types of trials in this experiment: exposure trials and probe (test) trials (Figure 1B). The exposure trials included one of three possibilities: risk and win (Riskwin), risk and lose (Riskloss), or no risk (Norisk), depending on participants’ choices and outcomes. Immediately following each exposure trial, a probe trial was presented. Our previous study has shown that participants (irrespective of their risk preference) would make a risky choice on most of the RA trials and seldom risk on the RD trials, whereas the risk rate on the FG trials varied significantly across participants (Xue, et al. 2009). Accordingly, the FG trials were used as probe trials to provide a sensitive measure of the prior outcome effect. RA and RD trials were used as exposure trials. For the purpose of the present study, half of the RA trials (where participants were most likely to gamble) were predetermined as win trials and the other half as loss trials, if participants chose to gamble. For all other trials, the computer would randomly choose one cup and determine whether they won or lost (It should be noted that although our manipulation slightly increased the probability of win for the RA trials, this did not significantly change the overall probability of a win. Post-experiment debriefing indicated that participants did not notice this manipulation, nor did they change their gambling strategies accordingly). The FG trials followed different types of exposure trials and were strictly matched in several decision parameters, including expected value, risk (defined as reward variance), reward probability and reward amplitude. Thus any behavioral and neural differences observed in these trials could only be attributed to the prior outcome manipulation. Since the structure of the exposure trials and the probe trials was identical and participants were simply told to decide whether or not to take each gamble, participants were not aware of the differences between the two types of trials, nor were they aware of the purpose of the study. Participants were told in advance that their final payoff would be randomly chosen (by flipping a coin) from one of the two fMRI runs, which was to avoid the wealth effect, i.e., participants’ decisions are affected by how much they have earned through the course of the experiment.
MRI Procedure
Participants lay supine on the scanner bed, and viewed visual stimuli back-projected onto a screen through a mirror attached onto the head coil. Foam pads were used to minimize head motion. Stimulus presentation and timing of all stimuli and response events were achieved using Matlab (Mathworks) and Psychtoolbox (www.psychtoolbox.org) on an IBM-compatible PC. Participants’ responses were collected online using an MRI-compatible button box. An event-related design was used in this fMRI study. To separate the neural responses associated with the decision from those associated with feedback processing, each trial was divided into three stages: Decision, Response and post-decision, and Feedback (Figure 1A). Random jitters were added between each stage and the sequence was optimized for design efficiency (Dale 1999) using an in-house program. At the Decision stage, a gamble was presented on the screen and participants were asked to contemplate the gamble without committing to any button response. After a varied period of delay (mean 3s, ranging from 1.5 to 5s), the response cue (“Yes” and “No” on each side) was shown on the screen and participants were to indicate their choice by pressing a button within 3 seconds, otherwise they would lose $1. The spatial position of the response cue varied from trial to trial so that participants were not able to predict its position and plan any motor response at the decision stage. After the response and some delay (mean 4s, ranging from 2.5 to 6s), a 0.5s feedback was presented to inform participants of the outcome. The next trial would begin after a jittered delay (mean 2.5s, ranging from 1 to 4s). In total, each run included 72 trials and lasted 12 minutes. Participants finished two runs of the gambling game.
MRI Data Acquisition
fMRI imaging was conducted in a 3T Siemens MAGNETOM Tim/Trio scanner in the Dana and David Dornsife Cognitive Neuroscience Imaging Center at the University of Southern California. Functional scanning used a z-shim gradient echo EPI sequence with PACE (prospective acquisition correction). This specific sequence is dedicated to reduce signal loss in the prefrontal and orbitofrontal areas. The PACE option can help reduce the impact of head motion during data acquisition. The parameters are: TR = 2000 ms; TE = 25 ms; flip angle =90°; 64 × 64 matrix size with resolution 3×3 mm2. Thirty-one 3.5 mm axial slices were used to cover the whole cerebral cortex and most of the cerebellum with no gap. The slices were tilted about 30 degree clockwise along the AC-PC plane to obtain better signals in the orbitofrontal cortex. The anatomical T1-weighted structural scan was done using an MPRAGE sequence (TI =800 ms; TR = 2530 ms; TE = 3.1 ms; flip angle 10; 208 sagittal slices; 256 × 256 matrix size with spatial resolution as 1×1×1mm3).
Image preprocessing and Statistical Analysis
Image preprocessing and statistical analysis were carried out using FEAT (FMRI Expert Analysis Tool) version 5.98, part of the FSL package (FMRIB software library, version 4.1, www.fmrib.ox.ac.uk/fsl). The first four volumes before the task were automatically discarded by the scanner to allow for T1 equilibrium. The remaining images were then realigned to compensate for small residual head movements that were not captured by the PACE sequence (Jenkinson and Smith 2001). Translational movement parameters never exceeded 1 voxel in any direction for any subject or session. All images were denoised using MELODIC independent components analysis within FSL (Tohka, et al. 2008). Data were spatially smoothed using a 5-mm full-width-half-maximum (FWHM) Gaussian kernel. The data were filtered in the temporal domain using a non-linear high pass filter with a 100-s cut-off. A three-step registration procedure was used whereby EPI images were first registered to the matched-bandwidth high-resolution scan, then to the MPRAGE structural image, and finally into standard (MNI) space, using affine transformations (Jenkinson and Smith 2001). Registration from MPRAGE structural image to standard space was further refined using FNIRT nonlinear registration (Andersson, et al. 2007a; Andersson, et al. 2007b). Statistical analyses were performed in the native image space, with the statistical maps normalized to the standard space prior to higher-level analysis.
The data were modeled at the first level using a general linear model within FSL’s FILM module. The following six trial types were modeled: three contextual trial types (Riskwin, Riskloss and Norisk) and their respective follow-up probe trials. Each trial was modeled as three distinct events, corresponding to the different stages of the trial: Decision, Response/post-decision, and Feedback. The event onsets were convolved with canonical hemodynamic response function (HRF, double-gamma) to generate the regressors used in the GLM. Temporal derivatives were included as covariates of no interest to improve statistical sensitivity. Null events were not explicitly modeled, and therefore constituted an implicit baseline. In this paper, we were particularly interested in BOLD responses associated with decision making after Riskwin and Riskloss. No significant result was found at the response stage for the probe trials.
A higher-level analysis created cross-run contrasts for each subject for a set of contrast images using a fixed effect model. These were then input into a random-effect model for group analysis using ordinary least squares (OLS) simple mixed effect with automatic outlier detection (Woolrich 2008). Group images were thresholded using cluster detection statistics, with a height threshold of z > 2.3 and a cluster probability of P < 0.05, corrected for whole-brain multiple comparisons using Gaussian Random Field Theory (GRFT).
To explore the relationship between neural activities and behavioral decision biases across participants, we conducted voxelwise correlation between the neural changes when making a decision after Riskloss compared to that after Riskwin and the behavioral decision bias. A relatively liberal threshold (p < .001, uncorrected) was used for this analysis to show some interesting, although preliminary, trends of behavior-brain relationship.
Region-of-interest (ROI) analyses
To qualitatively show the activation differences across conditions, non-independent ROIs were created from clusters of voxels with significant activation in the voxelwise analyses. Using these regions of interest, ROI analyses were performed by extracting parameter estimates (betas) of each event type from the fitted model and averaging across all voxels in the cluster for each subject. Percent signal changes were calculated using the following formula: [contrast image/(mean of run)] × ppheight × 100%, where ppheight is the peak height of the hemodynamic response versus the baseline level of activity (Mumford 2007).
Behavioral data analysis
Following Shiv et al. (2005), a lagged logistic regression analysis was conducted to examine the effect of prior outcome (gain vs. loss) on the subsequent decision. In this analysis, we again focused on the probe trials following either a gain or a loss. The dependent variable in this analysis was whether the decision was to gamble (coded as 1) or not (coded as 0). The independent variables were prior outcomes (coded as 1 if subjects won the previous gamble, and 0 if they lost the previous gamble), and participant-specific dummies (e.g., dummy 1, coded as 1 for participant 1, 0 otherwise; dummy 2, coded as 1 for participant 2, 0 otherwise and so on).
In addition, to quantify the gambler’s fallacy at the level of the individual participant, the gambler’s fallacy bias was calculated by subtracting the risk rate after Riskwin from that after Riskloss, which was then correlated with the imaging data. The risk rate for trials following a Norisk trial was not considered.
Results
Risky behaviors were modulated by prior outcomes
The lagged regression analysis revealed that there was a significant effect of prior outcome (χ2(1) = 4.943, p < 0.03), indicating that participants made significantly more risky choices after losses than after wins, a pattern resembling the gambler’s fallacy. This is a very strong effect considering it was acquired after a single win or loss, and the gambler’s fallacy usually becomes stronger as the loss streak increases (e.g., Ayton and Fischer 2004).
Consistently, by comparing the risk rate of the probe trials after Riskwin and after Riskloss, our data revealed participants on average made significantly more risky choices after losing the prior gamble than after winning it (36% vs. 29%, t(13) = 2.20, p <0.05). Still, there were significant individual differences: Although the majority of subjects showed a gambler’s fallacy pattern, a few subjects showed an opposite pattern (gambler’s fallacy bias ranging from −12% to 30%). This score was then correlated with the brain data to explore the possible neural mechanisms underlying this individual variation.
Imaging Results
The effect of prior outcome on subsequent decisions
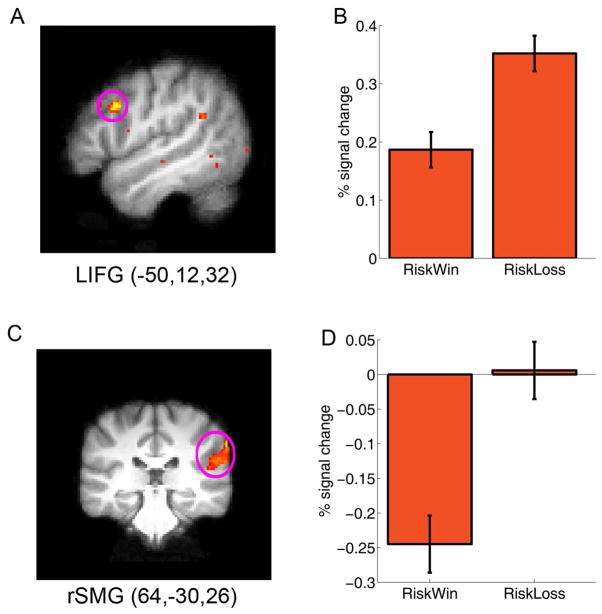
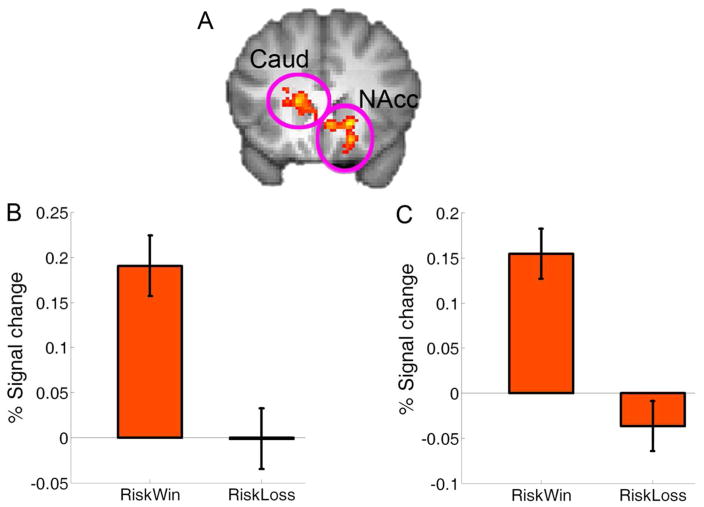
When comparing the brain responses associated with decisions after losing the previous gamble (i.e., Riskloss) to decisions after winning it (i.e., Riskwin), we found increased activation in the right supramarginal gyrus (peak MNI: 68,− 30,38, Z = 4.28) and the left inferior frontal gyrus (IFG) which extended to the middle frontal gyrus (MNI: −50,12,32, Z = 4.08, p < .001, uncorrected) (Figure 2). In contrast, the left caudate (MNI, −16,22,10; Z = 3.86) and right NAcc (MNI, 8,22, −4; Z = 3.52) showed increased activation when making decisions after winning a gamble than after losing a gamble (Figure 4A).
Fig. 2.
Fronto-parietal network and behavioral decision bias. The left inferior frontal gyrus (lIFG) and the right supramarginal gyrus (rSMG) showed significantly stronger activation while making a decision after losing a gamble than after winning a gamble. The results are overlain on the (A) sagittal and (C) coronal slice of the group mean structural image. All activations were thresholded using cluster detection statistics, with a height threshold of z > 2.3 and a cluster probability of P < 0.05, corrected for whole-brain multiple comparisons. B and D show the plots of percentage signal change for each ROI defined around the local maxima (see methods). Error bars denote within-subject error. Please note that the ROIs were non-independent and the absolute value should be treated cautiously.
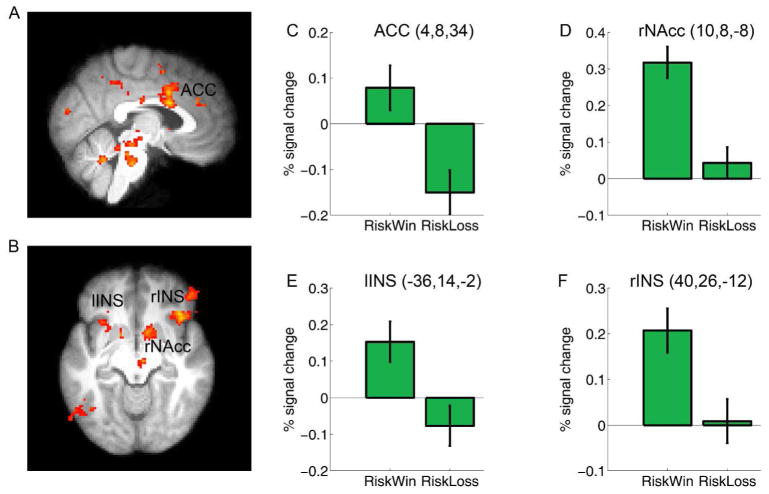
Fig. 4.
Brain activation associated with Feedback processing. The dopamingeric reward system and the insula were more active for Riskwin than for Riskloss (See main text). Group data (thresholded at Z > 2.3, whole-brain cluster-corrected at p < .05 using Gaussian Random Field Theory) are overlain on the (A) saggital and (B) axial slices of the group mean structural image. C to F show the plots of percentage signal change for each ROI defined around the local maxima (see methods). Error bars denote within-subject error. ACC: anterior cingulate cortex; NAcc: nucleus accumbens; Ins: Insula. Please note that the ROIs were non-independent and the absolute value should be treated cautiously.
At a liberal threshold (p < .001, uncorrected), we found that there were positive correlations between the behavioral bias (Riskloss - Riskwin) and the neural response increases in the left IFG/MFG (MNI: −38,38,8; Z = 3.43), the right SMG (MNI: 52, −40,24; Z = 4.12) and the right OFC (MNI: 32,48, −8, Z = 4.17), indicating that participants who showed more fronto-parietal activations when making decisions after Riskloss, as compared to decisions after Riskwin, were more likely to exhibit the bias of making more risky choices following a loss than following a win. In contrast, participants showing more right amygdala (MNI: 16, −4, −12, Z = 2.87) activation when making decisions after Riskloss than after Riskwin were less likely to show the loss-win or gambler’s fallacy. In addition, participants showing more caudate activation (MNI: −12,20,2, Z = 3.10) when making decisions after Riskwin than after Riskloss exhibited a pattern that shifted away from the gambler’s fallacy. These results, obtained with uncorrected p-values, indicate important trends in the data for potential future investigation.
The reward and arousal system was modulated by decision outcomes
To confirm that the prior outcome effect was driven by different brain responses associated with prior outcomes (win vs. loss), we contrasted the neural responses in the feedback stage of Riskwin and Riskloss trials. Consistent with other studies (Delgado, et al. 2000; Kable and Glimcher 2007; O’Doherty, et al. 2001; Rolls 2000; Tom, et al. 2007; Xue, et al. 2009), this analysis revealed significant activations in the dopaminergic reward system, including the ACC (MNI: 4,8,34; Z = 3.70) which extended to the dorsal paracingualte cortex (MNI: 0,18,44; Z = 4.25), the right nucleus accumbens (NAcc: 10,8, −8; MNI: Z = 3.54), the posterior cingulate cortex (PCC) which extended to the precuneus (MNI: −10, −56, −46; Z = 4.57), and the midbrain (MNI: −4, −28, −20; Z = 4.02). The left (MNI: −28,22, −6; Z = 3.34) and right insula (MNI: 40,26, −12; Z = 3.9) were also more active in the feedback stage of Riskwin trials than in Riskloss trials (Figure 5A&B), consistent with their roles in processing gains (Delgado, et al. 2000; Elliott, et al. 2000; Izuma, et al. 2008). Interestingly, stronger insular activation has also been reported for near miss trials (when play icon stopped one position from the payline), as compared to full miss trials (where the play icon stopped more than one position from the payline) in a simulated slot machine game (Clark, et al. 2009).
We further examined whether the neural response at the feedback stage could predict subsequent decision making across subjects. At an uncorrected threshold (P < .001), we found that there was positive correlation between the feedback-related neural response difference (Riskloss - Riskwin) and the subsequent behavioral bias (Riskloss - Riskwin) in the left dorsal lateral prefrontal cortex (MNI: −44,36,20, Z = 3.97), which further confirms the role of the lateral prefrontal cortex in the gambler’s fallacy.
Discussion
Using a task that simulates risk-taking in real-life, the present study demonstrated a behavioral phenomenon resembling the gambler’s fallacy in this group of young healthy participants: They made more risky choices after losing a gamble (Riskloss) than after winning a gamble (Riskwin). The behavioral results of the current study are consistent with many previous reports that participants’ risky decisions in a series of independent gambles were affected by previous outcomes (Ayton and Fischer 2004; Campbell-Meiklejohn, et al. 2008; Clark, et al. 2009; Croson and Sundali 2005; Gilovich, et al. 1985; Laplace 1820; Paulus, et al. 2003; Rabin 2002).
Going further by examining whole-brain activity with functional imaging, our study revealed that decisions after Riskloss were associated with increased activation in the frontoparietal network, and a lack of activation in the ventromedial prefrontal cortex and amygdala. In fact, there was a trend that activation in the amgydala was negatively correlated with the gambler’s fallacy bias, whereas that in the left dorsolateral frontal lobe was positively correlated with the gambler’s fallacy. This suggests that the gambler’s fallacy is a condition characterized by (1) more reliance on the executive processes of the prefrontal cortex, which are more dependent on the lateral regions of the prefrontal cortex, and (2) less engagement of the mesial prefrontal areas and amygdala that are essential for affective decision-making. The imaging results of our study corroborate prior studies with lesion patients emphasizing the role of affect and emotion in modulating decisions based on previous outcomes (Bechara, et al. 2003; Bechara, et al. 1999; Bechara, et al. 2000b; Bechara, et al. 1995; Bechara, et al. 1996; Shiv, et al. 2005). Specifically, patients with brain lesions that included the mesial orbitofrontal cortex (OFC)/ventromedial prefrontal cortex continued to make risky choices after a series of losses (Shiv, et al. 2005). The convergent evidence from functional brain imaging studies and lesion patient studies adds to the cumulative evidence arguing for a critical role for affect and emotion in decision-making (Bechara and Damasio 2005; Loewenstein, et al. 2001; Slovic, et al. 2005).
The lateral frontal network has been implicated in cognitive control mechanisms that support flexible, goal-directed behaviors, e.g., “executive functions”, which include conflict resolution (Barber and Carter 2005; Bunge, et al. 2002; Derrfuss, et al. 2005; Derrfuss, et al. 2004; Xue, et al. 2008a; Xue, et al. 2008b), reversal learning and inhibition of prepotent responses (Aron, et al. 2003; Aron, et al. 2004; Cools, et al. 2002; Dias, et al. 1996; Rolls 2000; Xue, et al. 2008a; Xue, et al. 2008b), as well as working memory (Braver, et al. 1997; D’Esposito, et al. 2000; Smith and Jonides 1999). In contrast, the mesial frontal network and amygdala have been implicated in affective decision-making. More importantly, other evidence has shown that the relationship between these lateral and mesial networks is asymmetrical in nature (Bechara, et al. 2000a), in that poor executive functions and working memory can lead to poor affective decision-making. However, poor affective decision-making can occur while executive functions and working memory are normal and highly functioning. The current results are consistent with this notion in that the driving force behind the gambler’s fallacy is the relatively stronger reliance on the lateral frontal network and its mechanisms of executive functions, with weaker engagement of the mesial frontal regions and their mechanisms of affective decision-making.
We also found that subjects showed more activation in the dorsal (i.e., caudate) and ventral striatum (i.e., NAcc) when they made decisions after wins than after losses. This suggests that even for decisions involving independent events, human decision-making is also modulated by a reinforcement learning mechanism supported by the ventral and dorsal striatum. Consistently, it has also been found that near-miss trials compared to full-miss trials involved stronger activation in the reward system, which was also associated with stronger desire to continue to gamble (Clark, et al. 2009). The striatum has been implicated in choice-outcome contingency learning via feedback, particularly in processing the prediction errors that lead to changes in behavioral choices (Daw, et al. 2006; O’Doherty, et al. 2004; Schultz 2002; Tricomi, et al. 2004; Xue, et al. 2008b). This mechanism allows behaviors with positive errors (e.g., wins) to be reinforced, whereas those with negative errors (e.g., losses) to be avoided. The gambler’s fallacy is a condition where this mechanism of prediction error is impaired (i.e., people risked more after losses), which is consistent with the notion that error prediction signaling linked to dopamine release in the striatum may lead to pathological gambling (Frank, et al. 2007).
The present study raises several interesting questions that can be examined in future studies. First, although existing literature primarily focuses on the effect of a series of losses on subsequent decisions, the gambler’s fallacy could be partially the result of reduced risk-seeking after a gain and/or increased risk-taking after a loss. Presumably, these different aspects of the gambler’s fallacy might involve distinct cognitive and neural mechanisms. Future studies need to find a good baseline condition to examine how gain and loss differently affect subsequent decisions.
Second, it is important to examine empirically in a normal population whether people with immature VMPFC (e.g., adolescents and children) are more prone to the gambler’s fallacy compared to those with normal VMPFC. Another empirical test that can be carried out is whether older adults, with declining prefrontal cortex functions (Hedden and Gabrieli 2004), would demonstrate a lower proneness to the gambler’s fallacy. Existing data seem to be consistent with this prediction: Participants in our study, as well as Knutson et al. (2008)’s study (mean age around 22 yrs old) showed an overall behavioral pattern consistent with the gambler’s fallacy, whereas the older healthy controls in Shiv et al. (2005)’s study (average 51.6 yrs old) gambled less after losses.
Third, we anticipate that individuals with psychological traits or psychiatric diagnoses that have been linked to dysfunctions of the VMPC and impaired reinforcement learning (e.g., pathological gamblers or addictive disorders), are more likely to exhibit the gambler’s fallacy. Indeed, whereas social gamblers might quit after losing a certain amount of money, a compulsive gambler will keep going, risking losing much more than they can afford in an effort to recover their losses. While often termed as “loss chasing”, this might also be partly explained by the gambler’s fallacy. It has been shown that resisting “loss chasing” is associated with strong activation in the brain regions associated with anxiety and conflict monitoring, including the anterior cingulate cortex and insula (Campbell-Meiklejohn, et al. 2008). Results from the present study provide preliminary evidence that “loss chasing” might also result from impaired affective decision making after previous losses and/or impaired reinforcement-learning signals. Our study provides a useful theoretical and methodological framework that can be used to examine pathological gamblers and addictive disorders from the point of view of the gambler’s fallacy and its underlying neural mechanisms.
Finally, the gambler’s fallacy can also be affected by the illusion of being in control, which is the tendency for human beings to believe that they can control, or at least influence, the outcomes that they in fact have no influence over (Langer 1975). Field data showed that, if given the opportunity to choose the number on the roulette game, many people would increase the bet after a gain, but on a different number (Croson and Sundali 2005). This lack of illusion of control in our study could have enhanced the gambler’s fallacy (also see Clark, et al. 2009). That is, when not being allowed to bet on another cup, the ‘optimal’ decision is thus to not gamble after winning a gamble, since the chance for the computer to choose the first cup again was “smaller” after it had been chosen on the previous trial. It might be reasonable to suggest that if participants are asked to guess which cup contains a reward, the same group of young participants might show less gambler’s fallacy. Further neuroimaging studies need to examine how the manipulation of illusion of control changes neural activities in the systems concerned with affective decision-making and the ability to exert self-control and “willpower”, i.e., the prefrontal cortex (Bechara 2005).
In sum, our results emphasize the limitations of the human cognitive system in making decisions involving random events. Although the human brain is equipped with powerful pattern detection and executive functions that support flexible “goal-directed” behaviors, as a result of evolution in coping with the pattern-abundant environment, these mechanisms might turn out to be maladaptive when a series of events adjacent in time and space are in fact independent (Ivry and Knight 2002). Although a lot of studies examined whether the cold cognitive system or the hot emotional system is better in making decisions, our study corroborates the cumulative evidence in showing that both the cognitive and emotional systems could lead to good or bad decisions under certain circumstances (e.g., Shiv et al., 2005). Future studies need to explore the exact mechanisms of emotion and cognition in decision-making and to discover how to optimize human decisions by setting the proper contexts that fit the way our brain works.
Fig. 3.
The striatum and behavioral decision bias. (A) The left caudate (Caud) and the right nucleus accumbens (NAcc) showed significantly stronger activation when making a decision after Riskwin than after Riskloss (Z > 2.3, whole-brain cluster-corrected at p < .05 using Gaussian Random Field Theory), which are overlain on the coronal slice of the group mean structural image. B and C show the plots of percentage signal change for the left caudate and right NAcc ROI, respectively. Error bars denote within-subject error. Please note that the ROIs were non-independent and the absolute value should be treated cautiously.
Acknowledgments
The research in this study was supported by the following grants from the National Institute on Drug Abuse (NIDA): DA11779, DA12487, and DA16708, and by the National Science Foundation (NSF) Grant Nos. IIS 04-42586 and SES 03-50984. We wish to thank Dr. Jiancheng Zhuang for help in fMRI data collection.
Footnotes
Competing interests statement: The authors declare that they have no competing financial interests.
References
- Andersson J, Jenkinson M, Smith S. Non-linear optimisation. FMRIB technical report TR07JA1. 2007a www.fmrib.ox.ac.uk/analysis/techrep.
- Andersson J, Jenkinson M, Smith S. Non-linear registration, aka Spatial normalisation. FMRIB technical report TR07JA2. 2007b www.fmrib.ox.ac.uk/analysis/techrep.
- Aron A, Fletcher P, Bullmore T, Sahakian B, Robbins T. Stop-signal inhibition disrupted by damage to right inferior frontal gyrus in humans. Nature Neuroscience. 2003;6(2):115–116. doi: 10.1038/nn1003. [DOI] [PubMed] [Google Scholar]
- Aron A, Robbins T, Poldrack R. Inhibition and the right inferior frontal cortex. Trends in Cognitive Sciences. 2004;8(4):170–177. doi: 10.1016/j.tics.2004.02.010. [DOI] [PubMed] [Google Scholar]
- Ayton P, Fischer I. The hot hand fallacy and the gambler’s fallacy: Two faces of subjective randomness. Memory & Cognition. 2004;32(8):1369–1378. doi: 10.3758/bf03206327. [DOI] [PubMed] [Google Scholar]
- Barber AD, Carter CS. Cognitive Control Involved in Overcoming Prepotent Response Tendencies and Switching Between Tasks. Cereb Cortex. 2005;15(7):899–912. doi: 10.1093/cercor/bhh189. [DOI] [PubMed] [Google Scholar]
- Bechara A. Decision making, impulse control and loss of willpower to resist drugs: a neurocognitive perspective. Nat Neurosci. 2005;8(11):1458–63. doi: 10.1038/nn1584. [DOI] [PubMed] [Google Scholar]
- Bechara A, Damasio AR. The somatic marker hypothesis: A neural theory of economic decision. Games and Economic Behavior. 2005;52(2):336–372. [Google Scholar]
- Bechara A, Damasio AR, Damasio H, Anderson SW. Insensitivity to future consequences following damage to human prefrontal cortex. Cognition. 1994;50(1–3):7–15. doi: 10.1016/0010-0277(94)90018-3. [DOI] [PubMed] [Google Scholar]
- Bechara A, Damasio H, Damasio AR. Emotion, decision making and the orbitofrontal cortex. Cereb Cortex. 2000a;10(3):295–307. doi: 10.1093/cercor/10.3.295. [DOI] [PubMed] [Google Scholar]
- Bechara A, Damasio H, Damasio AR. Role of the amygdala in decision-making. Ann N Y Acad Sci. 2003;985:356–69. doi: 10.1111/j.1749-6632.2003.tb07094.x. [DOI] [PubMed] [Google Scholar]
- Bechara A, Damasio H, Damasio AR, Lee GP. Different contributions of the human amygdala and ventromedial prefrontal cortex to decision-making. J Neurosci. 1999;19(13):5473–81. doi: 10.1523/JNEUROSCI.19-13-05473.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bechara A, Damasio H, Tranel D, Damasio AR. Deciding advantageously before knowing the advantageous strategy. Science. 1997;275(5304):1293–5. doi: 10.1126/science.275.5304.1293. [DOI] [PubMed] [Google Scholar]
- Bechara A, Tranel D, Damasio H. Characterization of the decision-making deficit of patients with ventromedial prefrontal cortex lesions. Brain. 2000b;123 (Pt 11):2189–202. doi: 10.1093/brain/123.11.2189. [DOI] [PubMed] [Google Scholar]
- Bechara A, Tranel D, Damasio H, Adolphs R, Rockland C, Damasio AR. Double dissociation of conditioning and declarative knowledge relative to the amygdala and hippocampus in humans. Science. 1995;269(5227):1115–8. doi: 10.1126/science.7652558. [DOI] [PubMed] [Google Scholar]
- Bechara A, Tranel D, Damasio H, Damasio AR. Failure to respond autonomically to anticipated future outcomes following damage to prefrontal cortex. Cereb Cortex. 1996;6(2):215–25. doi: 10.1093/cercor/6.2.215. [DOI] [PubMed] [Google Scholar]
- Braver T, Cohen J, Nystrom L, Jonides J, Smith E, Noll D. A parametric study of prefrontal cortex involvement in human working memory. Neuroimage. 1997;5(1):49–62. doi: 10.1006/nimg.1996.0247. [DOI] [PubMed] [Google Scholar]
- Bunge S, Hazeltine E, Scanlon M, Rosen A, Gabrieli J. Dissociable contributions of prefrontal and parietal cortices to response selection. Neuroimage. 2002;17(3):1562–1571. doi: 10.1006/nimg.2002.1252. [DOI] [PubMed] [Google Scholar]
- Campbell-Meiklejohn DK, Woolrich MW, Passingham RE, Rogers RD. Knowing When to Stop: The Brain Mechanisms of Chasing Losses. Biological Psychiatry. 2008;63(3):293–300. doi: 10.1016/j.biopsych.2007.05.014. [DOI] [PubMed] [Google Scholar]
- Clark L, Lawrence A, Astley-Jones F, Gray N. Gambling Near-Misses Enhance Motivation to Gamble and Recruit Win-Related Brain Circuitry. Neuron. 2009;61(3):481–490. doi: 10.1016/j.neuron.2008.12.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cools R, Clark L, Owen A, Robbins T. Defining the neural mechanisms of probabilistic reversal learning using event-related functional magnetic resonance imaging. Journal of Neuroscience. 2002;22(11):4563. doi: 10.1523/JNEUROSCI.22-11-04563.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Croson R, Sundali J. The gambler’s fallacy and the hot hand: Empirical data from casinos. Journal of Risk and Uncertainty. 2005;30(3):195–209. [Google Scholar]
- D’Esposito M, Postle B, Rypma B. Prefrontal cortical contributions to working memory: evidence from event-related fMRI studies. Experimental Brain Research. 2000;133(1):3–11. doi: 10.1007/s002210000395. [DOI] [PubMed] [Google Scholar]
- Dale AM. Optimal experimental design for event-related fMRI. Human Brain Mapping. 1999;8(2–3):109–114. doi: 10.1002/(SICI)1097-0193(1999)8:2/3<109::AID-HBM7>3.0.CO;2-W. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Daw ND, O’Doherty JP, Dayan P, Seymour B, Dolan RJ. Cortical substrates for exploratory decisions in humans. Nature. 2006;441(7095):876–9. doi: 10.1038/nature04766. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Delgado MR, Nystrom LE, Fissell C, Noll DC, Fiez JA. Tracking the hemodynamic responses to reward and punishment in the striatum. J Neurophysiol. 2000;84(6):3072–7. doi: 10.1152/jn.2000.84.6.3072. [DOI] [PubMed] [Google Scholar]
- Derrfuss J, Brass M, Neumann J, von Cramon D. Involvement of the inferior frontal junction in cognitive control: meta-analyses of switching and Stroop studies. Human Brain Mapping. 2005;25(1):22–34. doi: 10.1002/hbm.20127. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Derrfuss J, Brass M, Yves von Cramon D. Cognitive control in the posterior frontolateral cortex: evidence from common activations in task coordination, interference control, and working memory. Neuroimage. 2004;23(2):604–612. doi: 10.1016/j.neuroimage.2004.06.007. [DOI] [PubMed] [Google Scholar]
- Dias R, Robbins T, Roberts A. Dissociation in prefrontal cortex of affective and attentional shifts. 1996. [DOI] [PubMed] [Google Scholar]
- Elliott R, Friston KJ, Dolan RJ. Dissociable neural responses in human reward systems. J Neurosci. 2000;20(16):6159–65. doi: 10.1523/JNEUROSCI.20-16-06159.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frank M, Scheres A, Sherman S. Understanding decision-making deficits in neurological conditions: insights from models of natural action selection. Philosophical Transactions of the Royal Society B: Biological Sciences. 2007;362(1485):1641. doi: 10.1098/rstb.2007.2058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gilovich T, Vallone R, Tversky A. The hot hand in basketball: On the misperception of random sequences. Cognitive Psychology. 1985;17(3):295–314. [Google Scholar]
- Hedden T, Gabrieli JDE. Insights into the ageing mind: a view from cognitive neuroscience. Nat Rev Neurosci. 2004;5(2):87–96. doi: 10.1038/nrn1323. [DOI] [PubMed] [Google Scholar]
- Huettel S, Mack P, McCarthy G. Perceiving patterns in random series: dynamic processing of sequence in prefrontal cortex. Nature Neuroscience. 2002;5:485–490. doi: 10.1038/nn841. [DOI] [PubMed] [Google Scholar]
- Ivry R, Knight R. Making order from chaos: the misguided frontal lobe. Nature Neuroscience. 2002;5:394–396. doi: 10.1038/nn0502-394. [DOI] [PubMed] [Google Scholar]
- Izuma K, Saito DN, Sadato N. Processing of social and monetary rewards in the human striatum. Neuron. 2008;58(2):284–94. doi: 10.1016/j.neuron.2008.03.020. [DOI] [PubMed] [Google Scholar]
- Jenkinson M, Smith S. A global optimisation method for robust affine registration of brain images. Med Image Anal. 2001;5(2):143–56. doi: 10.1016/s1361-8415(01)00036-6. [DOI] [PubMed] [Google Scholar]
- Kable JW, Glimcher PW. The neural correlates of subjective value during intertemporal choice. Nat Neurosci. 2007;10(12):1625–33. doi: 10.1038/nn2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Knutson B, Wimmer GE, Kuhnen CM, Winkielman P. Nucleus accumbens activation mediates the influence of reward cues on financial risk taking. Neuroreport. 2008;19(5):509–13. doi: 10.1097/WNR.0b013e3282f85c01. [DOI] [PubMed] [Google Scholar]
- Langer E. The illusion of control. Journal of Personality and Social Psychology. 1975;(32):311–328. [Google Scholar]
- Laplace P. In: Philosophical Essays on Probabilities. Truscott FW, Emory FL, translators. New York: Dover; 1820. [Google Scholar]
- Levin I, Weller J, Pederson A, Harshman L. Age-related differences in adaptive decision making: Sensitivity to expected value in risky choice. Judgment and Decision Making. 2007;2(4):225–233. [Google Scholar]
- Loewenstein GF, Weber EU, Hsee CK, Welch N. Risk as feelings. Psychol Bull. 2001;127(2):267–86. doi: 10.1037/0033-2909.127.2.267. [DOI] [PubMed] [Google Scholar]
- Mumford J. A Guide to Calculating Percent Change with Featquery. Unpublished Tech Report. 2007 http://mumford.bol.ucla.edu/perchange_guide.pdf.
- O’Doherty J, Dayan P, Schultz J, Deichmann R, Friston K, Dolan RJ. Dissociable roles of ventral and dorsal striatum in instrumental conditioning. Science. 2004;304(5669):452–4. doi: 10.1126/science.1094285. [DOI] [PubMed] [Google Scholar]
- O’Doherty J, Kringelbach ML, Rolls ET, Hornak J, Andrews C. Abstract reward and punishment representations in the human orbitofrontal cortex. Nat Neurosci. 2001;4(1):95–102. doi: 10.1038/82959. [DOI] [PubMed] [Google Scholar]
- Odean T. Are investors reluctant to realize their losses? Journal of Finance. 1998:1775–1798. [Google Scholar]
- Paulus MP, Rogalsky C, Simmons A, Feinstein JS, Stein MB. Increased activation in the right insula during risk-taking decision making is related to harm avoidance and neuroticism. Neuroimage. 2003;19(4):1439–48. doi: 10.1016/s1053-8119(03)00251-9. [DOI] [PubMed] [Google Scholar]
- Rabin M. Inference By Believers in the Law of Small Numbers*. Quarterly Journal of Economics. 2002;117(3):775–816. [Google Scholar]
- Rolls ET. The Orbitofrontal Cortex and Reward. Cereb Cortex. 2000;10(3):284–294. doi: 10.1093/cercor/10.3.284. [DOI] [PubMed] [Google Scholar]
- Roney C, Trick L. Grouping and gambling: a Gestalt approach to understanding the gambler’s fallacy. Canadian journal of experimental psychology. 2003;57(2):69–75. doi: 10.1037/h0087414. [DOI] [PubMed] [Google Scholar]
- Schultz W. Getting Formal with Dopamine and Reward. Neuron. 2002;36(2):241–263. doi: 10.1016/s0896-6273(02)00967-4. [DOI] [PubMed] [Google Scholar]
- Sharpe L, Tarrier N. Towards a cognitive-behavioural theory of problem gambling. The British Journal of Psychiatry. 1993;162(3):407–412. doi: 10.1192/bjp.162.3.407. [DOI] [PubMed] [Google Scholar]
- Shiv B, Loewenstein G, Bechara A, Damasio H, Damasio AR. Investment behavior and the negative side of emotion. Psychol Sci. 2005;16(6):435–9. doi: 10.1111/j.0956-7976.2005.01553.x. [DOI] [PubMed] [Google Scholar]
- Slovic P, Peters E, Finucane ML, Macgregor DG. Affect, risk, and decision making. Health Psychol. 2005;24(4 Suppl):S35–40. doi: 10.1037/0278-6133.24.4.S35. [DOI] [PubMed] [Google Scholar]
- Smith E, Jonides J. Storage and executive processes in the frontal lobes. Science. 1999;283(5408):1657. doi: 10.1126/science.283.5408.1657. [DOI] [PubMed] [Google Scholar]
- Tohka J, Foerde K, Aron AR, Tom SM, Toga AW, Poldrack RA. Automatic independent component labeling for artifact removal in fMRI. Neuroimage. 2008;39(3):1227–45. doi: 10.1016/j.neuroimage.2007.10.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tom SM, Fox CR, Trepel C, Poldrack RA. The neural basis of loss aversion in decision-making under risk. Science. 2007;315(5811):515–8. doi: 10.1126/science.1134239. [DOI] [PubMed] [Google Scholar]
- Tricomi EM, Delgado MR, Fiez JA. Modulation of caudate activity by action contingency. Neuron. 2004;41(2):281–92. doi: 10.1016/s0896-6273(03)00848-1. [DOI] [PubMed] [Google Scholar]
- Woolrich M. Robust group analysis using outlier inference. NeuroImage. 2008;41(2):286–301. doi: 10.1016/j.neuroimage.2008.02.042. [DOI] [PubMed] [Google Scholar]
- Xue G, Aron AR, Poldrack RA. Common neural substrates for inhibition of spoken and manual responses. Cereb Cortex. 2008a;18(8):1923–32. doi: 10.1093/cercor/bhm220. [DOI] [PubMed] [Google Scholar]
- Xue G, Ghahremani DG, Poldrack RA. Neural substrates for reversing stimulus-outcome and stimulus-response associations. J Neurosci. 2008b;28(44):11196–204. doi: 10.1523/JNEUROSCI.4001-08.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xue G, Lu Z, Levin IP, Weller JA, Li X, Bechara A. Functional dissociations of risk and reward processing in the medial prefrontal cortex. Cereb Cortex. 2009;19(5):1019–27. doi: 10.1093/cercor/bhn147. [DOI] [PMC free article] [PubMed] [Google Scholar]