Why Is It Hard to Find Genes that are Associated with Social Science Traits? Theoretical and Empirical Considerations

Abstract

Though most behavioral traits are moderately to highly heritable, the genes that influence them are elusive: many published genetic associations fail to replicate. With physical traits like eye color and skin pigmentation, in contrast, several genes with large effects have been discovered and replicated. We draw on R.A. Fisher’s geometric model of adaptation to explain why traits of interest to behavioral scientists may have a genetic architecture featuring hundreds or thousands of alleles with tiny individual effects, rather than a few with large effects, and why such an architecture makes it difficult to find robust associations between traits and genes. In the absence of strong directional selection on a trait, alleles with large effect sizes will probably remain rare, and such a lack of strong directional selection is likely to characterize most traits currently of interest in social science. We evaluate these predictions via a genome-wide association study (GWAS) that carefully measured over 100 physical and behavioral traits with a sample size typical of candidate gene studies. While we replicated several known genetic associations with physical traits, we found only two associations with behavioral traits that met the nominal genome-wide significance threshold. We use the theory and findings to discuss (1) the challenges for social science genomics, particularly the likelihood that genes are connected to behavioral variation by lengthy, nonlinear, interactive causal chains; (2) the prospects for dealing with these challenges; and (3) the inherent tradeoff between two ways of meeting these challenges: increasing sample size and improving phenotype measurement.

Introduction

People differ in their intelligence, personality, and behavior, and a century of research in behavioral genetics leaves little doubt that some of this variation is caused by differences in their genomes.^1,2,3 Nonzero (and sometimes substantial) heritability of psychological traits has been consistently established in twin, adoption, and family studies that have often been massive in size. But beyond establishing that genes matter, such studies say little about the detailed genetic architecture of psychological traits, i.e., how many genetic polymorphisms affect a trait, how the polymorphisms interact, what they are, and what they do.

The recent advent of affordable genome-wide association studies (GWAS) offers the exciting opportunity to understand the genetic factors that influence psychological trait variation with far greater precision. It has the potential to uncover some of a given trait’s genetic architecture, including the number, genomic locations, average effects, and allele frequencies of the DNA variants that affect the trait. Even an incomplete understanding of a trait’s genetic architecture could prove a boon to social scientists for at least four reasons.⁴

First, the presence of genetic variants can be detected with high reliability. Thus, they may constitute direct measures of constructs that were previously regarded as only latent. For example, there is some evidence that a person’s genotype for the SNP in FTO associated with body mass index (BMI) may indicate a preference for certain kinds of high-calorie foods,⁵ and one might speculate that other genes may affect how much body weight is produced from a person’s caloric intake. These genetic variants could then be used as variables of interest, or as controls, in other models, testing models of the causation of obesity that formerly could only appeal loosely to “genetic factors.”

Second, the discovery of genetic associations may identify or clarify the actual biological mechanisms that underlie social and health behaviors. For example, a mechanistic role for the hormone oxytocin in trust-related behavior has been suggested by findings that variants in the oxytocin receptor gene (OXTR) are associated with differences in performance in a behavioral-economic trust game (albeit with mixed results so far).^6,7 And just as in medicine, where genetic discoveries have suggested new pathways for understanding and treating disease (e.g., Crohn’s disease⁸), genetic discoveries may help social scientists decompose crude concepts like “risk aversion” and “time preference,” both of which play roles in health behaviors, into biologically meaningful subcomponents.

Third, under very special circumstances, genetic variants could be used as instrumental variables that would identify causal relationships from non-experimental data. For such analysis to be valid, the allele must reliably and exclusively affect a specific biological trait (and no other biological traits). If these strong conditions are met, then one can use the random assignment (during meiosis) of each person’s genotype at that allele as a natural experiment to test the hypothesis that the biological trait, in turn, causes variation in some behavioral phenotype. For example, Chen and colleagues showed that SNPs in ALDH2 that are known to increase alcohol metabolism are associated with decreased blood pressure.⁹ This provides evidence that alcohol consumption in fact causes an increase in blood pressure—under the crucial, and perhaps implausible, condition that those SNPs are assumed not to also affect blood pressure through some other channel. Other studies of this type have been published,¹⁰ but it seems likely that the circumstances in which the instrumental variable approach can work are rare.

Fourth, knowledge of individuals’ genotypes could help in targeting social-science interventions to those who stand to benefit from them the most—an application of concepts from personalized medicine to public health and policy. Such a benefit is particularly likely to help children, since their abilities and preferences are less developed and harder to measure. For example, children with genotypes that confer a susceptibility to dyslexia might be offered personalized educational resources from a very early age.

The leap in precision from GWAS, compared to twin studies, promises to help not just working social and behavioral scientists but anyone interested in the evolutionary history and adaptive pressures that shaped the human species and its variation. Not only does an individual’s genome provide a partial recipe for the development of his or her unique phenome (set of phenotypes) forward in time, but our species’ array of genomic data provides a trace of our collective evolutionary history backward in time. For example, once it was discovered that mutations in the gene FOXP2 could cause a severe developmental deficit in speech and language, comparative genomic analyses showed that this gene’s sequence had changed at least twice since the separation of humans and chimpanzees from their common ancestor, that it has been a target of natural selection rather than a legacy of random drift, and that it is shared with Neanderthals—all relevant to venerable and hitherto nearly unresolvable debates on the evolution of language.

Despite the extraordinary promise of extending genetic research to behavioral traits, results so far of studies that have searched for genetic variants associated with these traits have been disappointing: No strong, replicable associations have been discovered. Most of the claims of genetic associations with such traits have turned out to be false positives, or at best vast overestimates of true effect sizes. Chabris et al. found that across three independent samples, only one of twelve published associations of particular genes with general intelligence replicated, and this one replicated in only one sample out of three.¹¹ Worse, the new samples were considerably larger than the originals, which suggests that all of these reports were probably false positives. Similarly, Benjamin, Cesarini, Chabris et al. found a SNP associated with educational attainment and cognitive function, but could not replicate it in three independent samples.⁴ Benjamin et al. likewise found no significant associations with any of a set of traits involving economic and political behavior.⁴ Finally, Beauchamp et al. conducted a GWAS of educational attainment (i.e., years of education completed) and found no hits that met conventional genome-wide significance levels; those that approached significance did not replicate in a second sample.¹²

Difficulty in finding specific genes that correlate with traits that are known to be heritable is not unique to the social sciences. It is also a problem in GWAS of medical traits such as psychiatric diagnoses and susceptibility to common diseases, and even with certain physical traits, such as height. Table 1 summarizes the heritabilities estimated from twin studies of medical, physical, and social science traits, based on three review articles and some recent publications in behavioral economics; it shows that the heritabilities of physical and psychological traits are similar and substantial.

Table 1.

Heritabilities of Selected Medical, Physical, and Behavioral Traits

Phenotype	Heritability	Source
Medical and Physical Traits:
Lipoprotein A level (age 17)	95%	Boomsma et al.82
LDL Cholesterol level (age 44)	69%	Boomsma et al.82
HDL Cholesterol level (age 44)	67%	Boomsma et al.82
Heart rate (age 17)	44%	Boomsma et al.82
Respiration rate (age 44)	61%	Boomsma et al.82
Testosterone level (age 17)		Boomsma et al.82
Males	66%
Females	41%
Birth weight	10%	Boomsma et al.82
Height (ages 16–adult)	80%*	Visscher et al.83
Behavioral Traits:
Problem behavior (age 3)		Boomsma et al.82
Externalizing
Males	49%
Females	73%
Internalizing
Males	61%
Females	66%
Personality Traits (adults)		Bouchard84
Neuroticism	48%
Extraversion	54%
Openness to Experience	57%
Agreeableness	42%
Conscientiousness	49%
General Cognitive Ability (age 18)	81%	Boomsma et al.82
Boredom susceptibility (age 18)	50%	Boomsma et al.82
Anxiety (age 18)	54%	Boomsma et al.82
Depression (age 18)		Boomsma et al.82
Males	39%
Females	53%
Smoking (yes/no, at age 18)		Boomsma et al.82
Males	66%
Females	32%
Alcohol Use (yes/no, at age 18)		Boomsma et al.82
Males	48%
Females	75%
Sports Participation (age 18)	47%	Boomsma et al.82
Religiosity (adults)	38%	Bouchard84
Specific religion practiced (age 18)	0%	Boomsma et al.,82 Bouchard84
Conservatism (adults)	55%	Bouchard84
Risk Attitudes		Cesarini et al.85
General willingness to take risk	21%
Willingness to take financial risk	26%
Risk aversion	34%
Portfolio volatility	25%	Cesarini et al.86
Cooperation		Cesarini et al.87
Trust	15%
Trustworthiness	18%
Income (single year)	38%	Taubman88
Income (single year)		Benjamin et al.4
Men	37%
Women	28%
Education (years)	28%	Taubman88
Behavioral Traits – Estimates Corrected for Measurement Error:
Risk Attitudes		Cesarini et al.85
General willingness to take risk	35%
Willingness to take financial risk	37%
Risk aversion	54%
Income (20-year average)		Benjamin et al.4
Men	58%
Women	46%

^*Estimated from genome-wide SNP data from twin and sibling pairs in Australia.

Notes: Estimates are averages of male and female heritabilities except when heritabilities are provided separately for both sexes (these are cases in which heritability differs by a large amount between males and females). Except in the third section, heritability estimates are not adjusted for differences in measurement error, longitudinal stability, or test-retest reliability of the phenotypes. Heritabilities may also vary with age; e.g., general cognitive ability becomes more heritable with age. Summaries of heritabilities of these and other phenotypes may be found in Plomin et al.,⁸⁹ Boomsma et al.,⁸² Bouchard,⁸⁴ and Barnea et al.⁹⁰

The discrepancy between the high heritability of both physical and psychological traits, and the rarity of replicable discoveries of particular genes for those traits, has been dubbed the problem of “missing heritability”.¹³ One possible resolution of this paradox is that each of the genes associated with a trait explains only a minuscule fraction of the total genetic variance—and hence these genes are difficult to identify statistically—but there is a huge number of such genes, and the heritability estimate reflects their aggregated effects.

Zuk et al. suggested that the discrepancy between heritability estimates from traditional biometrical studies of families and GWAS results thus far comes from the fact that biometrical studies will overestimate heritability if genes interact non-additively. ¹⁴ If this suggestion is correct, then it may be that GWAS approaches that do not grapple with the combinatorial explosion posed by the search for gene-gene interactions will fail to produce interesting results. This criticism of biometrical studies, however, only applies when such studies focus on only one type of kinship (e.g., twins reared together). Many human traits, including height and IQ, have been studied biometrically using many different kinds of kinships (twins reared together and apart, parents and offspring living together and apart, adoptive relatives who live together but are biologically unrelated). When these results are considered collectively, they converge on relatively large heritability values.

The evidence base for claims about heritability has been strengthened by a recently developed way to estimate heritability that examines genetic variation directly. The genomic-relatedness-matrix restricted maximum likelihood (GREML) technique¹⁵ uses all of the genotypic data from SNP arrays to estimate, for each pair of participants in a dataset, their degree of genetic similarity (relatedness), and then correlates genetic relatedness with phenotypic similarity across all of the pairs. Note that this technique does not require the participants to be related in the conventional genealogical sense of being siblings or cousins. It exploits the fact that all individuals within a population are distantly related, and that the level of relatedness varies considerably among pairs of people. For example, Davies et al. reported a GREML analysis with about 550,000 common SNPs and 3000 subjects in which about 45% of the variance in general cognitive ability could be directly explained by the SNP variation;¹⁶ Chabris et al. replicated this finding with a smaller sample.¹¹ In the original application of GREML, Yang et al. showed that 45% of the variance in height across 4000 subjects could be explained by ~300,000 common SNPs.¹⁵ These estimates leave room for unmeasured genetic variation (e.g., uncommon SNPs, other non-SNP polymorphisms) to explain additional heritability.

In this context, a “common” variant is a polymorphic site where the minor allele shows a frequency exceeding a certain threshold (say .05), whereas a “rare” variant is a site where the frequency of the minor allele falls below this threshold. The GREML results finding substantial heritability owed to common variants tend to discredit the hypothesis that missing heritability arises because common variants typically studied in GWAS are merely surrogates for rare variants of powerful effect that, if only they could be discovered, would account for much more heritability.¹⁷ Furthermore, Wray et al. provide a thorough analysis of the available GWAS results and show that a model relying exclusively on rare causal variants cannot account for the data.¹⁸ It is important to note that, under any reasonable evolutionary model, most genetic variants affecting a given phenotype may be rare. All else being equal, however, common variants contribute more variability than rare variants, and thus it is not at all inconsistent to expect that common variants will be responsible for a substantial portion of heritability.

Though medical and behavioral geneticists are becoming increasingly sympathetic to the many-common-genes-of-small-effect answer to the missing heritability question, it is still not known why such a diffuse polygenic architecture should be typical of quantitative traits. Nor is it known what might account for the exceptions that have been found.

A simple possible explanation invokes the length of the causal chain from genetic to phenotypic variation. For example, variation in pigmentation (e.g., of eyes, skin, and hair) arises from the number of melanosomes produced, as well as their size and shape, and the type of melanin synthesized.¹⁹ These biochemical differences follow directly from changes in the composition or regulation of gene products, which in turn are strongly influenced by differences in DNA sequence. Indeed, a single SNP in HERC2 is largely responsible for blue eye color.²⁰

In contrast, changes at the molecular and cellular level must be remote from their ultimate effects in most behavioral phenotypes, and even from many physical phenotypes such as body mass index (BMI). Consider that BMI may depend on what a person likes to eat, how often he eats, how much he exercises, details of his metabolism, and a host of other complex behaviors and physiological processes. Similarly, given that the physical basis of psychological attributes such as cognitive ability, conscientiousness, impulsivity, and risk aversion resides in intricate patterns of neural circuitry and interlocking biochemical feedback loops, we should perhaps expect any single genetic variant affecting such an attribute to contribute only a small fraction of the total variation in the phenotype.

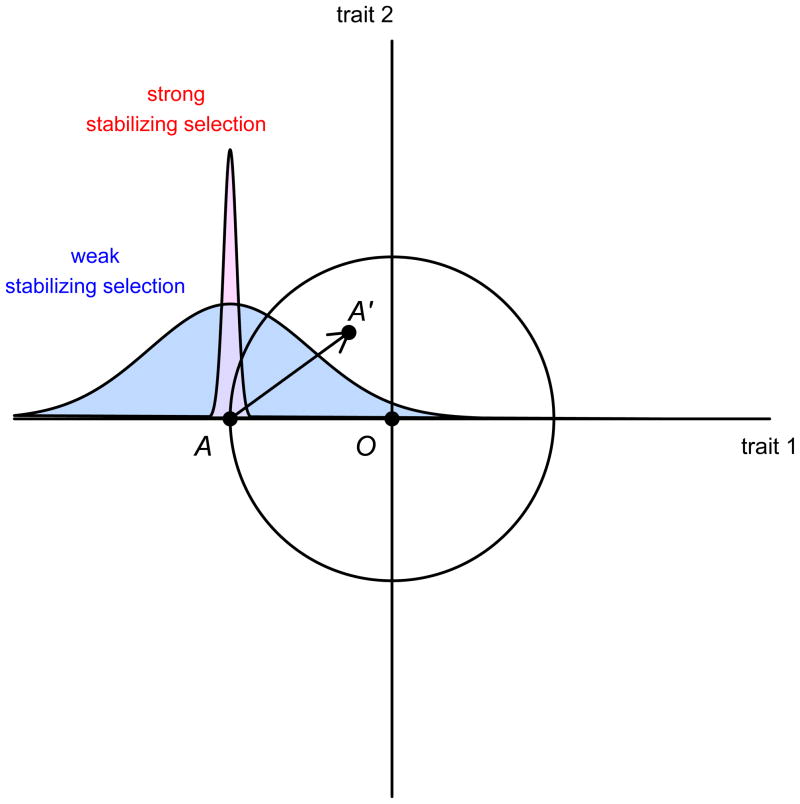
Here we offer a second explanation (which is not mutually exclusive with the first), which invokes the differential action of natural selection. More than 70 years ago, R.A. Fisher proposed a geometric model of adaptation²¹ that may be summarized in Figure 1, which depicts two quantitative traits as the vertical and horizontal dimensions on a two-dimensional space (representing a slice of the vast multidimensional space of possible phenotypes). Point A represents the current mean phenotype of the species (in this example, a low value of trait 1 and an intermediate value of trait 2). Point O represents the optimum favored by natural selection. Suppose that A was once optimal, because selection had pushed the population to its optimum value, but that O no longer coincides with A because an abrupt environmental change occurred that demands a different (in this case higher) value of trait 1.

Figure 1.

R.A. Fisher’s geometric model of adaptation.²¹ A is the current mean phenotype of the population, A′ is the mean phenotype that would result if the mutation denoted by the arrow were to be instantly fixed, and O is the new optimum favored by natural selection. The narrow distribution of trait 1 values around A is the situation that would prevail under strong stabilizing selection, while the broad distribution would prevail under weak stabilizing selection.

What would have to happen for selection to adapt the organism to the new optimum? One possibility is a new mutation arising in a single individual and, if beneficial, reaching fixation (100% allele frequency) in the population. In the model the fixation of a mutation corresponds to adding a vector of random direction to the population’s current trait-space position at A. This feature of the model captures two key observations: (1) mutations have no inherent tendency to increase the fitness of their bearers, and (2) any single mutation may affect several distinct traits, and therefore this mutation could change the population’s mean values of both traits 1 and 2. The subset of new phenotypes that would result in an increased level of adaptation is depicted in Figure 1 as the interior of the circle centered on O, representing all the combinations of trait values that are closer to the optimum (using the Euclidean distance metric).

The diagram also helps one understand the fates of mutations with different effect sizes. Note that any mutation whose effect on the traits exceeds the diameter of the circle would not be fixed, because it leaves the population farther from the optimum than when it started (point A). Selection would simply favor the status quo. In general, the smaller the mutation, the more likely it is to be beneficial, because there are many small moves that can be made from A that stay within the circle, but few very large ones—most large moves will overshoot the circle or move away from it. The fact that a smaller move is more likely to take the population into the circle should already be evident from Figure 1. As the number of traits/dimensions increases to larger values (which cannot be depicted in a two-dimensional figure), the greater ease with which smaller moves take the population into the “hypersphere” becomes quite dramatic.^*

Fisher argued that mutations of large effect are relatively unimportant in evolution, since they will rarely move a population closer to O. And the closer to the optimum the organism already is, the less likely large mutations are to be beneficial. Fisher draws an analogy to the process of focusing a microscope. When a microscope is already close to the correct focusing point, a small random perturbation of the knob is likelier than a larger perturbation to bring it closer to exact focus.

We will now expand Fisher’s argument to explain the puzzling contrast between some physical phenotypes like skin or eye color on the one hand and social science and medical phenotypes on the other. Suppose that trait 1 was previously under strong stabilizing selection and thus has negligible genetic variation at the time of the environmental shift that makes O the new optimum (this state of affairs would correspond to a tight clustering of trait 1 values around point A). Since the rate of the approach to the optimum via existing genetic variation (i.e., variation that does not result from de novo mutations) is bounded above by trait 1’s heritability (per the breeder’s equation),²² a population with negligible genetic variability in that trait is unlikely to adapt quickly towards O unless a mutation of large effect arises and reaches fixation—e.g., a mutation that took the population to A′, where its new value for trait 1 is much closer to the optimum.

Alternatively, suppose that stabilizing selection on trait 1 had been much weaker, permitting the buildup of substantial genetic variation (leading to a wide scatter of trait 1 values around A). In this case a mutation of large effect is far less likely to become common through positive selection. At the same time that this mutation is struggling to increase its frequency, the existing genetic variation is enabling the population to adapt toward O. If O lies within the current range of genetic variation (which is true for trait 1 under the assumption of the more variable population in Figure 1) and selection is even moderately strong, then the population mean shifts from A to O even without the arrival of a mutation of large effect. As the population evolves, the diameter of the circle bounding all points of higher adaptation continuously shrinks. Once the magnitude of the mutation that would have taken the population to A′ exceeds the diameter of the circle, the mutation is disfavored and is very likely to be eliminated from the population.^†

To complete our explanation, we need to assume that the polymorphic sites contributing to existing genetic variation tend to be small in effect. Even under weak stabilizing selection, variants of large effect experience greater selection pressure and consequently are more likely to be found at a low minor allele frequency.^25–27 This implies that any common (i.e., high-frequency) variants contributing to standing genetic variation will typically be small in effect. Thus, we might expect many loci of small effect to explain most of the heritable variation underlying a quantitative trait—unless there was recent selection for the trait that was strong relative to the initial variability. If a trait turns out to be associated with many genetic loci of small effect and few or no loci with large effects, then we would have evidence that this trait has not experienced such selection.

In the remainder of this paper, we will show how this evolutionary analysis can help epidemiologists and social scientists make sense of the genetics of behavior in the era of rapidly expanding genome scans. We report the results of our own GWAS of more than a hundred human phenotypes, both physical phenotypes such as body size and pigmentation, and behavioral phenotypes of great interest to social scientists, such as general intelligence, memory ability, verbal fluency, impulsivity, risk aversion, fairness, and utilitarianism. We measured a wide variety of cognitive, personality, and behavioral-economic traits so that we could generalize across types of traits and compare the behavioral to the physical phenotypes. In other words, without sampling freckles, eye color, and height in a single study, we could not make general claims about physical traits; without measuring religiosity, memory, and impulsiveness in a single study, we could not make general claims about behavioral traits; and without measuring both categories we could not compare them. To our knowledge this study is the first to examine associations between a genome-wide panel of single-nucleotide polymorphisms (SNPs) and such a broad spectrum of phenotypes; almost all previous association studies of behavioral traits have examined only one or a few candidate genes and phenotypes. In addition to including both physical and behavioral traits, the study examined traits that are expected to be both monogenic and polygenic. An additional innovation is that the behavioral phenotyping was intensive, relying not just on standardized paper-and-pencil tests but on individual computerized tasks, sometimes administering hundreds of trials to quantify a single trait. This step is essential because crude measurement of behavioral traits could lead to false negatives and thus would not help explain the puzzling failure to find associated genes. Thus, each of our 419 participants was tested individually in a laboratory session lasting an average of 3.5 hours.

To preview the results: Despite an adequate sample size for detecting large effects and despite high-precision measurements, we found few associations between SNPs and traits at an appropriately stringent significance threshold. Since many of our measured phenotypes (including our behavioral phenotypes) are known to be heritable,²⁸ the absence of strong associations in our data indicates that—aside from pigmentation—both physical and behavioral traits are mainly affected by numerous genes with small effects.

After presenting the results, we discuss their implications for future genetic association studies of behavioral traits, which are likely to become ever more common as the cost of genotyping and sequencing declines. In addition to our analysis of the evolutionary genetics of heritable variation, we introduce two other key issues in designing and interpreting such studies: the effects of selection bias for participant inclusion in such studies, and the tradeoffs between measurement error and statistical power in selecting simple, fast, inexpensive assessments of a traits versus the sort of complex, time-consuming, and potentially expensive assessments that we conducted.

Methods

Participants were recruited, and data and samples were collected, at two sites: Harvard University in Cambridge, MA, and Union College in Schenectady, NY. Efforts were made to recruit from the surrounding communities a more representative sample than the typical college student population: Paper fliers were posted at various public locations, advertisements were placed in free newspapers and on Craigslist, and the study was made available to the Psychology Department Study Pool at Harvard.

Participants first completed an online screening questionnaire that included items regarding age, medical history, and grandparental ethnicity. Participants who were younger than 18 or older than 45, or who reported a history of bipolar disorder, schizophrenia, or severe head trauma were excluded. To help control for ancestral confounding of genotypes and trait levels,²⁹ we recruited a sample of predominantly Western European ancestry, which was ascertained at the screening process by asking potential participants to list the country of origin or ancestry for each of their biological grandparents. A total of 419 participants provided complete, usable genetic and phenotypic data.

Eligible participants were invited to either the Harvard or Union lab for a data collection session lasting typically from three to four hours. Participants gave informed consent after the nature of the procedure had been fully explained to them. A diverse set of cognitive, personality, economic, attitude, demographic, and physical phenotypes were collected via computerized tasks, paper-and-pencil surveys, and face-to-face interaction. DNA was collected via two mouthwash samples in the lab, and then extracted and genotyped elsewhere. Population stratification was investigated and controlled for in all genetic analyses reported here. We used the program PLINK for genotypic data cleaning and analyses.³⁰ (See for a complete list of phenotypes, descriptions of select phenotypes, and details of DNA collection, extraction, genotyping, and analysis of population stratification.)

Linear regression was performed to test for purely additive association between SNPs and all polytomous and continuous traits. Logistic regression was performed for dichotomous traits. We chose the standard genome-wide significance threshold of 5×10⁻⁸ for declaring a SNP-trait association to be statistically significant.³¹ Under a frequentist approach aiming to minimize the chance that even a single declared “hit” is a false positive, the large number of examined traits would require an even more stringent threshold. However, we follow the suggestion of the Wellcome Trust Case-Control Consortium,³² who adopt a quasi-Bayesian justification for retaining the standard genome-wide significance threshold; it maintains a constant ratio of true to false positives as the number of markers and traits increases (so long as statistical power and prior probabilities for any given association do not change). Moreover, since our primary goal is to compare results across phenotypes, what is most important is to have a common threshold across phenotypes, and adopting the standard threshold maximizes comparability of our results with other published results.

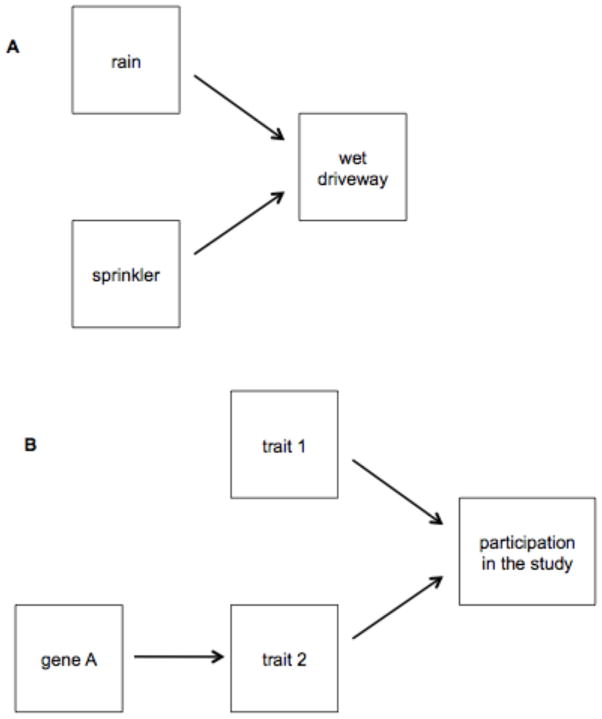
For any SNP showing an association with a trait at the significance threshold 5×10⁻⁸, we re-ran PLINK with our cognitive ability composite and NEO Openness, Neuroticism, and Agreeableness factor scores as additional covariates in an effort to control for selection bias.³³ Selection bias may be an underappreciated contaminant in gene-trait association studies.³⁴ To understand the bias, consider this analogy: Suppose that a driveway will be wet in the morning as the consequence of two possible causal mechanisms: whether it rained last night, and whether a sprinkler was activated (Figure 2A). Suppose also that the two causal variables are independent; that is, taking all days into account, there is no correlation between whether it rains and whether the sprinkler turns on. If we only consider mornings on which the pavement is wet, however, we will spuriously conclude that the two causes are negatively correlated. For instance, if we see that the pavement is wet and we know that it did not rain last night, we can be confident that the sprinkler was activated. We only see the true non-correlation when we consider all days. Suppose that the probability of rain and the probability of sprinkler activity are both 0.5 and are independent. If one checked the driveway every morning, wet or dry, then one would observe rain and no sprinkler a quarter of the mornings, sprinkler and no rain a quarter of the mornings, both a quarter of the mornings, and neither a quarter of the mornings—the lack of association is apparent. Now suppose one checked only the mornings with wet driveways. On a majority of the mornings (two-thirds), one would discover either rain with no sprinkler or a sprinkler with no rain. In other words, one would find a negative correlation, but only because those mornings that would have diluted the correlation to zero were excluded. The basic principle emerging from this example is that if one inadvertently conditions an observation on the common effect (is the driveway wet?) of multiple causes (rain or sprinkler), one can counterfactually create the illusion of a non-zero correlation among the causes.^‡

Figure 2.

Examples of directed acyclic graphs containing a “collider” (the common effect of two or more causes).³³ Conditioning on observing a collider alters the apparent covariation among the causes; for example, two independent causes that are uncorrelated when all observations are considered can appear to be negatively correlated when only observations containing the collider are considered.

This same principle applies in GWAS. Suppose that high levels of either trait 1 or 2 are independent causes of a person ending up as a participant in our study, either because the trait affects whether the person decides to volunteer or it affects whether we decide to include his or her data (Figure 2B). Then we will spuriously find any gene that affects trait 2 to be associated with trait 1, even if trait 1 is not at all affected by genetic variation. That is because among people who participate in the study, traits 1 and 2 will appear to be (negatively) correlated, and therefore a cause of scoring high on trait 2 will appear to also be a cause of scoring low on trait 1. Controlling for the other traits affecting participation may not fully solve the problem (even if we know what these traits are), because the trait of interest may itself be connected to the other participation-related traits in a complex causal graph, and therefore the decision to condition linearly on the other traits could in principle introduce further bias. In practice, however, conditioning on traits that may affect study participation is likely to be a conservative procedure. For example, if one trait mediates the genetic effect of another, then controlling for the mediating trait will suppress the genuine effect of the genetic variant on the downstream trait of interest, and therefore is unlikely to generate additional false positives.

We performed a numerical simulation to illustrate the extent to which selection bias may distort GWAS results. We stipulated two initially independent traits affecting participation in the study; the sum of an individual’s z-scores on these traits needed to exceed 3 in order for the individual to be in the pool of participants. This corresponds to slightly less than two percent of the general population being available to participate. We believe that this simulated situation is not so farfetched as a model of some ongoing projects (e.g., the Personal Genome Project;³⁶ 23 and Me³⁷). We stipulated that each trait has a heritability of 0.50 and is affected by loci all with allele frequency 0.50 and average effect (regression coefficient) 0.05; each causal locus thus account for 0.25% of the variance in its trait. The results were striking: The estimated effects of the true causal variants with respect to a given trait were centered at 0.03—off by 40%. Similarly, the “effects” of the variants on the wrong trait (of the two traits, the one that the variants did not affect) were centered at −0.02. In a situation where it is important to distinguish miniscule effects from zero, a spurious effect of 0.02 cannot be considered trivial. Although more thorough numerical and analytical investigations are certainly worthwhile, this example illustrates that researchers performing GWAS of behavioral traits should be aware of the consequences of selection bias.

Table 2 includes the sample statistics for the Multidimensional Attribute Battery (MAB) and NEO personality inventory, two instruments used in our study that have detailed population norms. Compared to the norming samples for the MAB, our participants show much higher means and smaller standard deviations, suggesting that cognitively able individuals were more likely to participate in the study. The relationship between the NEO personality traits and study participation is more complex. Our study participants show conspicuously higher levels of Openness than the norming samples. The trait of Openness is defined by a willingness to examine new ideas and try new activities, and thus it is plausible that higher levels of this trait may be a cause of volunteering for scientific research. Our study participants also show consistently lower levels of Neuroticism and higher levels of Agreeableness. (Interestingly, our study participants are more variable than the norming samples, perhaps because people with higher cognitive ability are more variable in their responses to personality questionnaires.³⁸) Furthermore, the fact that students were overrepresented among our participants indicates that the selection bias may have already operated extensively at an earlier point. That is, even if we could have taken a random sample of all students attending the top 200 colleges (say), the process of college admissions would still have exerted considerable selection bias distinguishing this special population from its larger age cohort. As a reasonable attempt to control for selection bias, then, we will use general cognitive ability, Openness, Neuroticism, and Agreeableness as additional covariates whenever a novel SNP-trait association shows a significant p-value. Without doing this, we might spuriously find, for example, that a gene associated with greater Openness was also negatively associated with all the traits that are correlated with Openness, such as political liberalism (see below).

Table 2.

Characteristics of the sample in age, sex, general cognitive ability (MAB scales), and personality traits (NEO Five-Factor Inventory scales).

Trait	mean	SD
age (years)	25.2	6.44
sex	67.6% female
MAB Arithmetic	.797 (0)	.836 (1)
MAB Similarities	1.054 (0)	.601 (1)
MAB Vocabulary	1.386 (0)	.891 (1)
NEO Neuroticism (college, female)	21.90 (25.83)	8.38 (7.59)
NEO Neuroticism (adult, female)	18.71 (20.54)	9.13 (7.61)
NEO Neuroticism (college, male)	18.53 (22.49)	10.04 (7.92)
NEO Neuroticism (adult, male)	18.84 (17.60)	10.46 (8.61)
NEO Extraversion (college, female)	30.10 (31.27)	6.89 (5.64)
NEO Extraversion (adult, female)	29.19 (28.16)	7.55 (5.82)
NEO Extraversion (college, male)	29.08 (29.22)	6.10 (5.97)
NEO Extraversion (adult, male)	29.70 (27.22)	8.64 (5.85)
NEO Openness (college, female)	34.02 (27.94)	6.57 (5.72)
NEO Openness (adult, female)	34.42 (26.98)	5.57 (5.87)
NEO Openness (college, male)	31.79 (27.62)	6.57 (6.08)
NEO Openness (adult, male)	31.36 (27.09)	7.04 (5.82)
NEO Agreeableness (college, female)	33.80 (31.00)	5.51 (5.33)
NEO Agreeableness (adult, female)	34.42 (33.76)	4.71 (4.74)
NEO Agreeableness (college, male)	31.46 (28.76)	6.05 (5.24)
NEO Agreeableness (adult, male)	32.00 (31.93)	5.70 (5.03)
NEO Conscientiousness (college, female)	33.64 (31.02)	7.40 (6.53)
NEO Conscientiousness (adult, female)	32.29 (35.04)	7.15 (5.78)
NEO Conscientiousness (college, male)	30.17 (30.21)	6.54 (7.19)
NEO Conscientiousness (adult, male)	33.33 (34.10)	8.04 (5.95)

The summary statistics reported in the respective manuals are given in parentheses next to the corresponding sample statistics. The MAB scores were scaled as standard normal using the tables in the MAB manual.⁹¹ The NEO summary statistics were calculated for participants between the ages of 18 and 22 for purposes of comparison with the college norms in the NEO manual⁹² and for participants age 30 and over for comparison with the adult norms.

Results

As can be seen in Table 3, we found at least a marginal signal for all SNPs previously found to be associated with eye color, hair color, freckling, and skin color ^{19,37,39–42} (with the exception of one study that digitally quantified eye color⁴³) and that were either present in our cleaned set of genotyped SNPs or represented by a proxy SNP with an r² > .60. Note that despite our relatively small sample size, the effects of the intronic SNP rs12913832 in HERC2 on eye and hair color were statistically significant at the stringent, standard GWAS threshold.

Table 3.

Association results for pigmentation phenotypes.

trait	reported SNP	proxy SNP	r2	minor allele	sample MAF	HapMap MAF	effect size	p-value	gene
eye darkness	rs12913832			A	.222	.208	.998	2×10−68	HERC2
eye darkness	rs12896399	rs1075830	.615	A	.460	.308	.167	.003	SLC24A
eye darkness	rs1393350			A	.266	.192	−.154	.02	TYR
eye darkness	rs1408799			T	.313	.300	.095	.11	TYRP1
hair darkness	rs12913832			A	.223	.208	.840	1×10−13	HERC2
hair darkness	rs12896399	rs1075830	.640	A	.460	.308	.372	9×10−5	SLC24A4
hair darkness	rs12821256			C	.095	.142	−.352	.03	KITLG
red hair	rs1805007			T	.076	.147	7.44	2×10−6	MC1R
red hair	rs1015362			T	.278	.233	.507	.09	ASIP
freckling	rs1805007			T	.076	.147	.613	6×10−6	MC1R
freckling	rs1042602			A	.346	.417	−.223	.005	TY R
freckling	rs2153271	rs1416742	.949	G	.384	.373	−.139	.07	BNC2
freckling	rs619865			A	.098	.108	.178	.15	ASIP
skin darkness	rs1805007			T	.076	.147	−.267	.005	MC1R
skin darkness	rs1042602			A	.346	.417	−.118	.03	TY R
skin darkness	rs619865			A	.098	.108	−.156	.07	ASIP

Eye darkness was reported on a 3-point scale. Hair darkness was recorded on 9-point scale. Red hair was recorded as a dichotomous trait, and its effect size is reported as an odds ratio. Freckling and skin darkness were recorded on 5-point scales. All effect sizes for non-dichotomous traits are reported as the expected change in trait value per each additional copy of the minor allele. All alleles are coded according to NCBI build 36 coordinates on the forward strand.

A meta-analysis has identified over 180 genomic regions containing a variant affecting height.⁴⁴ Due to the weak effect of each individual variant, however, we did not replicate any of these loci with genome-wide significance. However, of the 94 loci either present in our set of SNPs or represented by a proxy, 65 loci had estimated effects with the correct sign and 29 did not (binomial test p < .0001). There is also an enrichment of low p-values; whereas only nine or ten p-values less than .10 were expected under the null distribution, we observed 16 (significantly more, according to a binomial test, p < .05). These trends are consistent with most of these loci being true positives despite our inability to extract a strong signal from them. A selection of the height variants showing marginal significance in our data is shown in Table 4A, along with the nonsynonymous SNP rs1815739 in ACTN3 that has been found to affect athletic performance.⁴⁵

Table 4A.

Association results for physical phenotypes.

trait	reported SNP	proxy SNP	r2	minor allele	sample MAF	HapMap MAF	effect size	p-value	gene
standing height	rs7460090			C	.134	.117	−.188	.07	SDR16C5
standing height	rs237743			A	.231	.308	.175	.04	ZNFX1
standing height	rs6439167			T	.201	.183	−.191	.03	C3orf47
standing height	rs889014			T	.347	.375	−.124	.10	BOD1
standing height	rs7274811	rs3213183	.692	A	.304	.267	−.140	.07	ZNF341
standing height	rs7759938	rs369065	1	C	.332	.364	.172	.02	LIN28B
standing height	rs3764419	rs9890032	.982	G	.401	.375	−.188	.009	ATAD5/RNF135
standing height	rs3791675			T	.228	.275	−.305	4 × 10−4	EFEMP1
standing height	rs724016			G	.428	.483	.121	.10	ZBTB38
standing height	rs1351394	rs7968682	.983	T	.499	.517	−.120	.10	HMGA2
strength	rs1815739	rs540874	1	A	.428	.458	.252	.006	ACTN3

Effect sizes for height are reported in standard deviation units. Note that these effect sizes tend to be inflated because of the “winner’s curse.” Strength was reported on a 5-point scale.

Another recent meta-analysis has identified 32 genomic regions containing a variant affecting body mass index (BMI).⁴⁶ BMI, even more than height, seems to be affected by many loci of small effect. Consistent with this view, 11 of the 17 known BMI loci represented in our data had estimated effect sizes of the correct sign; however, the wrong-signed loci were the most statistically significant.

Table 4B shows our results for a selection of SNPs previously reported to be associated with general cognitive ability,^47–51 personality,^52,53 working memory,⁵⁴ and episodic memory,⁵⁵ all of which we measured extensively. We observed little evidence for these associations in our own data. In concordance with a previous study,⁵⁶ we failed to replicate a reported association between a common SNP in the gene KIBRA and episodic memory, despite a putative functional validation in the original study both by an analysis of gene expression and by fMRI.⁵⁵ This suggests that most of the SNPs reported in earlier association studies of behavioral traits may either have been false positives or have overestimated effect sizes. Applying a threshold of 5×10⁻⁸, we did not observe any loci significantly associated with the traits in Table 4B.

Table 4B.

Association results for the behavioral phenotypes with previously reported SNPs.

trait	reported SNP	proxy SNP	r2	minor allele	sample MAF	HapMap MAF	effect size	p-value	gene
general cognitive ability	rs2760118	rs7775073	.982	G	.316	.317	.062*	.42	ALDH5A1
general cognitive ability	rs324650			T	.464	.467	.026	.72	CHRM2
general cognitive ability	rs363050			G	.444	.475	−.027	.72	SNAP-25
general cognitive ability	rs17571	rs17834326	.781	A	.083	.083	−.051*	.70	CTSD
general cognitive ability	rs760761	rs2619545	1	C	.196	.192	−.033*	.72	DTNBP1
Conscientiousness	rs2576037	rs7233515	.879	A	.400	.408	−.038	.60	KATNAL2
Neuroticism	rs12883384			A	.410	.317	−.014*	.85	MAMDC1
paired-associate recognition	rs17070145			T	.338	.267	.065	.37	KIBRA
3-back accuracy	rs4680			A	.449	.517	.027	.72	COMT

Effect sizes are reported in sample standard deviation units. An asterisk indicates that the estimated effect in our study had a sign opposite to what had been previously reported.

We did find a significant association between political conservatism and rs10952668 (Table 5). This SNP lies in LOC642355, a pseudogene on chromosome 7. Not surprisingly, the SNP also showed an association with the highly correlated trait of Democrat vs. Republican (β = .260, p < .02). We also observed a significant association between rs1402494, which lies in a gene desert on chromosome 4, and gambling frequency. These are the only two novel associations that reached genome-wide significance, and besides these, only eye color and hair color also produced significant associations.

Table 5.

Novel association results for behavioral phenotypes.

trait	reported SNP	minor allele	sample MAF	HapMap MAF	effect size	p-value
liberal vs conservative	rs10952668	T	.458	.392	.552 (.478)	2 × 108 (1 × 10−6)
gambling frequency	rs1402494	G	.206	.241	.278 (.276)	3 × 108 (6 × 10−8)

Liberal vs conservative was reported on a 7-point scale. Gambling frequency was reported on a 5-point scale. Effect sizes and p-values after adjustment for general cognitive ability, Openness, Neuroticism, and Agreeableness are given parenthetically. Note that effect estimates may be inflated as a result of the winner’s curse.

Interestingly, the SNP associated with political conservatism, rs10952668, also showed marginal evidence for association with the personality traits Openness (β = .142, p < .06) and Agreeableness (β = .130, p < .08), which are correlated positively with political liberalism.⁵⁷ Since the correlation is positive, contrary to findings from political psychology that conservatives tend to be less Open and Agreeable (in the sense of compassionate⁵⁸), these results raise the possibility that the association between rs10952668 and conservatism may be attributable to selection bias rather than the gene causing the personality traits typical of conservatives. (Since to our knowledge this potential selection artifact has not been discussed in the genetic epidemiology literature—although it has parallels in the effects of natural selection on linkage disequilibrium—we explore it at some length in the Discussion below.) After we added general cognitive ability, Openness, Neuroticism, and Agreeableness as covariates in an attempt to control for selection bias, the association of rs10952668 and conservatism diminished and fell short of significance. The association of rs1402494 and gambling frequency appears robust against our attempts to control for selection bias. We conclude that both of these associations must be replicated in much larger samples before they are accepted as true positives.

Discussion

The contrast between pigmentation and the other phenotypes examined in this study is striking (Tables 3–4). Given a significance threshold of 5×10⁻⁸, our study had statistical power approaching 0.80 to detect any locus accounting for more than 10% of the variance in any trait. We retained some power (0.12) for loci accounting for as little as 5% of the variance. The fact that we measured so many phenotypes implies that we should have obtained several hits if a large proportion of the phenotypes were indeed affected by such loci. Because we only obtained at most two new hits, however, loci with effects of this magnitude on the non-pigmentation traits we studied must be uncommon. In agreement with previous studies,^11,53,59,60 we conclude that cognitive ability, personality dimensions, social attitudes, and most other traits of interest to behavioral scientists are affected by numerous loci of small effect. In this respect the behavioral traits we studied resemble height and BMI rather than pigmentation.

How can we explain the differences in genetic architecture between the pigmentation traits and the other physical and behavioral traits? One possibility is that the architecture hinges on the length of the causal chain between gene and phenotype. Pigments, after all, are molecules, and you can change a molecule, thereby giving a person a different eye color, by changing a single gene. It’s not as easy to make a person more intelligent, utilitarian, altruistic, or impulsive by changing one gene, owing to the greater complexity in the mechanisms that lead a person to be intelligent or altruistic in the first place. With gross physical traits like BMI and height, the problem may be that there are too many ways that genes can directly affect the phenotype; indeed, it may be hard for a genetic change not to affect them, just as most changes to the features of (say) a car or laptop computer have consequences for its size and weight, which engineers have to trade off with many minute compensations.

The other explanation invokes the evolutionary model of the causes of genetic architectures we outlined earlier, which relates the effect size of genetic polymorphisms to the magnitude and recency of changes in the adaptively optimal level of the trait. After the loss of body hair in our lineage, pigmentation probably came under strong stabilizing selection in our ancestors, who needed protection from the African sun. More recently, the out-of-Africa migrants ancestral to Europeans and East Asians experienced a sudden and drastic shift in the optimal level of pigmentation—perhaps because of the need to sustain cutaneous synthesis of vitamin D in northern climates,⁶¹ although others have implicated sexual selection or as-yet unidentified evolutionary pressures.^62–64 In any event the result was that several depigmenting mutations of large effect increased rapidly in frequency.^65–67 Table 4A lists those mutations that have not yet reached fixation and are thus still polymorphic in Europeans.

No such recent environmental change—one with clear consequences for the direction and magnitude of the optimum—is apparent for other phenotypes such as height, BMI, and the behavioral traits we examined. Though differences in climate and food availability may select for different optima in body size and shapes, they fluctuate rapidly across space and time and may not show the consistent selection pressure that changes in latitude, altitude, and cloud cover apparently exerted on pigmentation. Intelligence is a highly general and universally adaptive trait, which can translate into fitness benefits (via successful problem-solving) in any environment. If human populations have long been at the optimum, then existing mutations are likely to be small in effect. Such variants are likely to be small in effect even if the optimum has changed over time—as may have happened in the cases of intelligence^68,69 and religiosity⁷⁰—so long as the change occurred very gradually. In particular, intelligence may be a highly general and universally adaptive trait, responding more to coevolutionary pressures exerted by language and sociality than to any sudden change in the physical environment. Personality traits, too, are far less predictably correlated with physical environments than are pigmentation traits.

Evolutionary game theory has established theoretical rationales for the persistence of multiple behavioral phenotypes (e.g., hawk and dove strategies) in the same population.^71,72 Analogously, the selective environment for personality may consist of the local distributions of the personalities of other people,⁷² and the mixture is unlikely to have changed in a systematic way with recent shifts in the human population.

Even if selection has acted on these traits since the dispersal of homo sapiens from Africa, the new optima could have been quickly reached by small shifts in allele frequency at many minor loci, leaving any major mutants at the low frequencies determined by the interaction of mutation, drift, and stabilizing selection.⁷³ As discussed above, the result of such dynamics would be the observed absence of common variants with large effects.

Our two proposals for explaining the pattern in Tables 3–5 lead to the following suggestions for future GWAS of behavioral traits. First, to understand the causal chain between genetic and phenotypic variation, we should try to narrow the chasm from both sides. Doing so requires seeking and validating endophenotypes that lie closer on the causal chain to genetic variation than the coarse and easily measured phenotypes we are used to. Second, researchers seeking variants of large effect should ideally study populations where directional selection may have recently produced a phenotypic change that is large relative to the initial standing variation. Recent studies of altitude adaptation in Tibetans exemplify both of these suggestions.^74–76 The genes successfully associated with red blood cell count and hemoglobin concentration in these studies would have been more difficult to identify if the phenotype had been characterized at a level as abstract as “altitude tolerance.” Moreover, the recent and rapid divergence of Han Chinese and Tibetans in altitude tolerance after the latter began to occupy a highland environment was plausibly driven by a selection differential large enough to pull variants of large effect away from the boundary of frequency zero. It is, however, an open question how many social-science traits can be studied by looking for recent directional selection.

As for traits with more typical evolutionary histories, the expectation of small effect sizes requires that much larger samples be ascertained than are common in social-science genetics research. We see two promising approaches. One is for researchers to take advantage of the potential for large sample sizes by allying with the burgeoning field of personal genomics, in which a large base of volunteers or consumers provide genotype and phenotype information.^37,77,78 It is crucial, though, to check these samples for selection biases, because many phenotypes of interest are likely to be causes of participation in personal genomics itself. For example, an individual with a liability to a particular disease may be strongly motivated to participate in a personal genomics study by self-interest or altruism; participants also must be wealthy enough to afford the service. We conjecture that our findings of elevated cognitive ability and intellectual openness among research volunteers will generalize to future studies. If so, it is prudent to collect reliable measurements of these traits in all GWAS that are not based on population samples and to note any unusual sample distributions on these traits when reporting SNP-trait associations.

The other approach is the traditional epidemiological study, which attempts to minimize the impact of personal characteristics on study participation by recruiting a population-based sample. This will remain an important complement to volunteer- and consumer-driven approaches.

Recall that Chabris et al. consulted three population-based studies and found that only one out of 12 published genetic associations with general intelligence could be replicated within them, and that one only one out of three times.¹¹ One explanation is that the original associations came from small convenience samples similar to the one we studied here.

There is, however, a tradeoff inherent in using large population-based studies for gene discovery. Most of these projects are directed towards medical outcomes rather than social-science traits (with some notable exceptions, such as the Health and Retirement Study, the Wisconsin Longitudinal Study, and the English Longitudinal Study of Aging; the first of these now has GWAS data available, and the others may soon). Data collection in these surveys, although often face-to-face and longitudinal, distributes time and effort across many phenotypes that are measured with short questionnaires (or even single questions). The disadvantage of such studies is that whenever the underlying trait of interest is continuous, quick or brief measures are inherently less reliable (i.e., are subject to more measurement error) than are more detailed ones.

Genetic association studies, then, present researchers with a tradeoff between using high-quality or high-technology (e.g., neuroimaging) measures of each phenotype, which are often only feasible for small samples, and having a large sample in which the phenotype is measured poorly. In social science research, this dilemma is commonly resolved in favor of smaller samples with higher quality measures—and perhaps for this reason, that is the strategy in most of the social-science genetic association studies conducted to date, including the one we reported here. But because the genetic architecture of behavioral traits is likely to feature very weak genetic associations, our intuitions regarding the appropriate research strategy may not be correct when carried over from non-genetic social science research, where effect sizes are typically much larger. There is as yet no straightforward way to calculate an expected effect size for genetic associations in social science, so the best we can do is to assume that effects will be similar to those found for other complex (polygenic) traits—tiny.

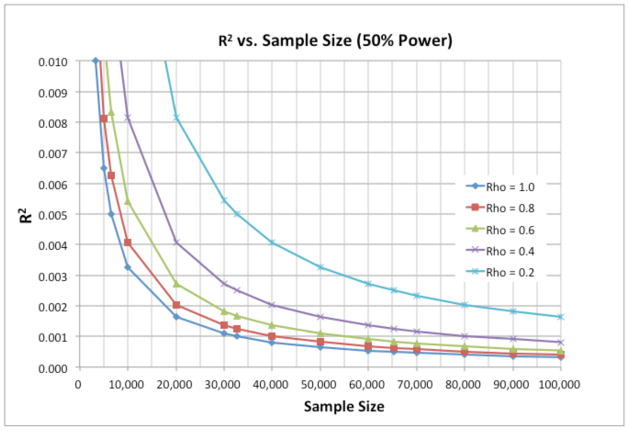
Figure 3 displays the results of a set of power calculations that quantify the tradeoff. The phenotype is assumed to be normally distributed. The y-axis shows effect sizes in terms of R², the fraction of variance in the phenotype explained by variation in a single genotype, ranging from 0 to 0.01 (one percent) in increments of 0.001 (one-tenth of one percent). The x-axis is the sample size. Each curve graphs the locus of effect-size/sample-size pairs that gives 50% power to detect the association at p = 5×10⁻⁸ for a given phenotype reliability. The phenotype reliability is measured in terms of the test-retest correlation, i.e., the correlation between two independent measurements of the phenotype. We consider the cases where reliability is equal to 1.0, 0.8, 0.6, 0.4, and 0.2.

Figure 3.

An illustration of how the reliability (measurement error, denoted here as Rho) of a phenotype affects the relationship between effect size of a genetic association and the sample size required to achieve 50% statistical power to detect the effect at the genome-wide significance threshold of 5×10⁻⁸. For example, if one expects a genotype to explain 0.4% of the variance in a trait (R² = .004), then a sample of about 10,000 subjects is required to achieve 50% power when reliability is 0.80, but a sample of 20,000 subjects is required if reliability is 0.40. That is, with a sample of 20,000 instead of 10,000, instruments that are only one-quarter as reliable provide the same power to detect the effect.

For the very small effect sizes that can be expected for behavioral traits, Figure 3 indicates that it will generally be better to sacrifice phenotype quality in favor of larger sample sizes. For example, consider an effect size of R² = 0.001 (0.1% of the variance). This is the size of the association found in a meta-analysis of the association between cognitive ability and variation in the COMT gene in 67 independent samples, and it is likely to be biased upward because the meta-analysis found evidence of publication bias.⁷⁹ Since cognitive ability is among the most reliably measured social science traits and since the meta-analysis found evidence of publication bias, such an effect size is likely to be representative of the largest associations we can expect for a behavioral trait. Given R² = 0.001, for a perfectly-measured phenotype (reliability = 1.0), 50% power requires a sample size of 30,000 individuals. This is far too large a sample to obtain high-quality measures of behavioral traits, which generally requires bringing the research subjects into a laboratory and conducting repeated tests spanning many minutes or hours. In contrast, for a phenotype with test-retest reliability of 0.6—which is typical of behavioral phenotypes measured by brief questionnaires—50% power requires a sample size of 50,000 individuals. Samples at least this large have recently become feasible. Medical datasets that have already collected GWAS data could much more easily add brief behavioral questionnaires to their ongoing data collections than onerous laboratory sessions. Since such medical datasets in aggregate comprise hundreds of thousands of participants, such a research strategy should be possible.⁴

Conclusions

We conducted a Genome-Wide Association Study on more than 100 carefully measured phenotypes in more than 400 subjects, but found very few loci of large effect associated with any trait other than the pigmentation of eyes and skin. This includes a substantial proportion of the traits that have been of theoretical interest to behavioral scientists in recent decades. Four points emerge from our analysis:

1. The genetic architecture of trait variation cannot be taken as constant across traits, particularly the expectation that a single gene or a small number of genes will have a noticeable effect on the trait. First, the shortness of the causal chain between the DNA and the trait matters a great deal, with single-gene effects being more likely for traits generated by a single protein or regulatory shift. Second, the genetic architecture of a trait is intimately intertwined with its evolutionary history. The implications flow in both directions: the discovery of an association between a gene and a trait can illuminate the evolution of our species, and the evolutionary process determines which associations we can most readily discovered. In particular, stabilizing selection of moderate strength, which permits a substantial background of weak or rare variants, supplies the fuel for polygenic adaptation and may obviate the need for mutations of large effect to arise after a sudden environmental change.

2. Many psychological traits of interest to researchers are themselves plausible causes of participation in scientific research, which raises the potential of spurious associations. Measuring such traits (e.g., cognitive ability and personality) and incorporating them into analyses is one strategy for dealing with this issue.

3. If there are two ways to measure a trait—a high-reliability measure that can be performed only on a small sample because of the required time, effort, and resources, versus a lower-reliability brief measure that can be administered to a large sample—power analyses suggest that using the lower-reliability measure with the larger sample size is likely to be the best strategy. Researchers interested in the genetic architecture of behavioral traits should therefore consider working with large-scale survey datasets such as the HRS, WLS, and ELSA, as well as medical-genetic studies that are willing to conduct social science surveys among their participants.

4. Genetic associations with behavioral traits have proven notoriously difficult to replicate. This is not because the relevant traits are not heritable or the original studies were poorly designed or knowingly underpowered; researchers at the time lacked the resources for conducting more genotyping and assembling larger samples, and they were hoping to find common alleles with large effect size. Our discussion of Fisher’s model, and the empirical experience accumulated in the first fifteen years of social science genetics, suggest that individual gene effect sizes for traits not under strong selection are likely to be extremely small, and therefore require extremely large datasets to be detected.

The fact that faster, cheaper, and more powerful methods of genotyping have led to fewer, smaller, and less reliable findings on the connection between genes and behavior, despite the near-certainty that such connections exist, stands as one of the disappointments of 21st century science. To make progress, we should shift away from the traditional model of epidemiology via statistical significance testing, in which large significant correlations are the standards of success and worthy of newspaper headlines, while negative results are considered a failure and destined for the file drawer. It has become increasingly clear that this practice has led to mischief both in epidemiology and in social science,^80,81 and it may also be preventing the discovery of important scientific insights. If we have learned that behavioral genetic variation is caused by many genes with effects that are too small to currently measure, then we have also learned something important about the physiology and evolutionary history of such traits. With nature as with people, the Yiddish expression may apply: No answer is also an answer.