Comparing CAL and PD for predicting periodontal disease progression in healthy sites of patients with chronic periodontitis using multi-state Markov models

Abstract

Aim

To understand degeneration of healthy sites and identify factors associated with disease progression in patients with chronic periodontitis.

Material and Methods

Data on healthy sites from 163 American and Swedish subjects were analyzed using two three-state (health, gingivitis, chronic periodontitis) Markov models based on bleeding on probing (BOP), and either clinical attachment level (CAL) + BOP or pocket depth (PD) + BOP.

Results

In two years, 10% (CAL + BOP) and 3% (PD + BOP) of healthy sites developed chronic periodontitis. On average, healthy sites remained healthy for 32 months before transiting in both models. Most transitions (87% - 97%) from health were to the gingivitis state. The expected duration of the gingivitis lesion was 4-5 months and sites recovered with a high probability (96% - 98%). Disease severity as measured by number of sites with CAL/PD > 4mm at baseline and smoking, were associated with fast progression from health to chronic periodontitis within 6 months as were gingival redness in the PD + BOP model only. With age, the rate of disease progression to gingivitis decreased.

Conclusions

Transition probabilities for gingivitis and chronic periodontitis were higher with CAL + BOP than with PD + BOP. Smoking and disease severity were significant predictors for fast progression.

The natural history of chronic periodontal disease can be viewed as a staged, slowly progressing disease process, from its earliest form when it is called gingivitis to its severe form characterized by irreversible pathological changes (periodontitis). First, healthy sites usually progress to gingivitis when oral hygiene practices are ignored. Secondly, if good oral hygiene is not restored, further destruction of the tissues often leads to periodontitis. In the context of plaque-induced periodontal diseases, healthy sites are characterized by little or no dental plaque present whereas gingivitis is characterized by accumulation of dental plaque and inflammation of the gingiva. In plaque-induced periodontitis, there is evidence of inflammation of the gingiva and loss of connective tissue and alveolar bone.

From a clinical perspective, a better understanding of the disease dynamics such as the expected time to reach a certain level of degeneration or the probability of progression may lead to more appropriate prevention management and treatment. Traditionally, risk factors associated with periodontitis are determined with the use of statistical measures such as odds ratios or relative risks. Another approach to model disease progression over time is to use a multi-state Markov model, which assumes that the study subjects reside in one of a finite set of health states (Kalbfleisch & Lawless 1985). The method is increasingly used in medical research because many diseases naturally evolve through stages of increasing severity (Jackson 2011). For example, the technique has been applied in research of HIV progression (Aalen et al. 1997), screening for abdominal aortic aneurysms (Jackson et al. 2003), liver cirrhosis (Andersen et al. 1991) and cancer progression (Kay 1986, Chen et al. 1996). In contrast, the use of multi-state Markov in dentistry models has been very limited. We have identified only two previous studies investigating the clinical course of periodontitis with use of Markov models; a 3-year study of staff volunteers at the University of Queensland (Faddy et al. 2000) and a 26-year study of Norwegian men (Schätzle et al. 2009). Both studies targeted populations without particular risk for periodontal diseases.

The use of Markov models for periodontal disease is particularly appealing because the disease is characterized by both advancement and repair over time, which cannot be handled using traditional statistical methods that focus on disease progression only. Instead, the Markov approach allows for a flexible representation where progression and regression may be estimated separately and influence of risk factors on particular transitions studied. For example, gingivitis symptoms may be temporary before healthy conditions are restored, implying that not all sites with gingivitis progress to chronic periodontitis. This idea is not new in periodontal studies. In 1984, Socransky et al. (1984) suggested that periodontal diseases progress by recurrent acute episodes. They coined this process “burst theory” and went further to suggest that there may be relatively short periods in which sites may undergo periodontal destruction followed by periods of extended remission.

It is generally accepted that the classification of periodontal diseases is extremely difficult and complex because different factors have to be considered. In 1989, the American Academy of Periodontology identified distinct types of periodontal diseases based on factors such as age at onset, clinical appearance, pathogenic microbiota, systemic influences and rate of disease progression (AAP 1989). A simpler classification was to follow at the 1st European Workshop in Periodontology in 1993 (Attström & van der Velden 1994), which was revised in 1996 (Armitage 1996). In the 1999 classification, seven major categories of periodontal diseases were listed (Annals of Periodontology 1999), emphasizing the multifactorial nature of the disease. At the 5th European Workshop of Periodontology, a three stage classification based on loss of attachment was introduced (Tonetti & Claffey 2005). Therefore, classification systems should be viewed as dynamic works-in-progress that need to be modified periodically based on current thinking and new knowledge.

There is a clear need for better knowledge about disease development in healthy sites in susceptible patients with periodontitis for implementing appropriate intervention plans. To help bridge this gap in the literature, we propose two continuous Markov models for periodontal disease progression over a discrete state space. The model includes three disease states: health, gingivitis and chronic periodontitis and allows for gingivitis recovery. We distinguish the disease states based on two well-established clinical markers; clinical attachment level (CAL) or periodontal pocket depth (PD) in combination with bleeding on probing (BOP). Due to the controversy regarding periodontal disease classification, we note that the model can be interpreted directly in terms of the clinical parameters without any reference to particular disease levels. We apply the model to longitudinal clinical data from patients with chronic periodontitis (Mdala et al. 2012, Goodson et al. 2012). The purpose of this article is to compare the use of CAL versus PD in studying periodontal disease dynamics of healthy periodontal sites in patients with chronic periodontitis and to assess the influence of various covariates on particular disease progression and regression transitions.

Material and Methods

Data

The data were derived from a 2-year clinical study, originally from 217 subjects undergoing treatment for chronic periodontitis, in Boston, USA and Gothenburg, Sweden. The subjects were randomized to the following treatment arms: 1) scaling+root planing (SRP); 2) SRP+surgery (SURG)+systemic amoxicillin (AMOX)+systemic metronidazole (MET); 3) SRP+SURG+local tetracycline (TET); 4) SRP+SURG; 5) SRP+AMOX+MET+TET; 6) SRP+AMOX+MET; 7) SRP+TET; and 8) SRP+SURG+AMOX+MET+TET. The subjects were assessed at the following time points: baseline, 3, 6, 12, 18 and 24 months. For more details concerning patients, inclusion and exclusion criteria, periodontal treatments and clinical monitoring, Mdala et al. (2012) and Goodson et al. (2012) should be consulted. We selected data from healthy sites in subjects with at least four completed visits. Healthy sites were defined by CAL/ PD ≤ 4 mm or PD ≤ 4 mm and no BOP at baseline. Of these sites, we then included only sites that were healthy at 6 months to allow for possible wash-out of effects of previous periodontal treatments.

For the CAL + BOP model, we analyzed data from 1,124 mesiobuccal sites in 162 subjects with a median age of 52 years (range 26 – 84 years). The data consisted of 622 site observations from 82 Americans and 502 site observations from 80 Swedish subjects. Data for the PD + BOP model consisted of 1, 374 mesiobuccal sites from 165 subjects with a median age of 54 (range 26 – 84 years). These data consisted of 639 site observations from 80 Americans and 735 site observations from 85 Swedish subjects. Other variables that were included in the analyses were age, gender, nationality (American or Swedish), current smoking habits, evidence of plaque accumulation, gingival redness and disease severity at baseline, defined as the number of teeth with CAL / PD ≥ 4 mm.

Disease classification

At each study visit, CAL, PD and BOP were assessed in the mesiobuccal site of each tooth. Based on the measurements, a site could belong to one of the three states; (1) health, (2) gingivitis and (3) chronic periodontitis (Fig. 1). We defined health and disease states as follows;

1. Health: CAL/ PD ≤ 4 mm and no BOP

2. Gingivitis: CAL/ PD ≤ 4.0 mm and BOP

3. Chronic periodontitis: CAL/ PD > 4 mm with or without BOP

Fig. 1.

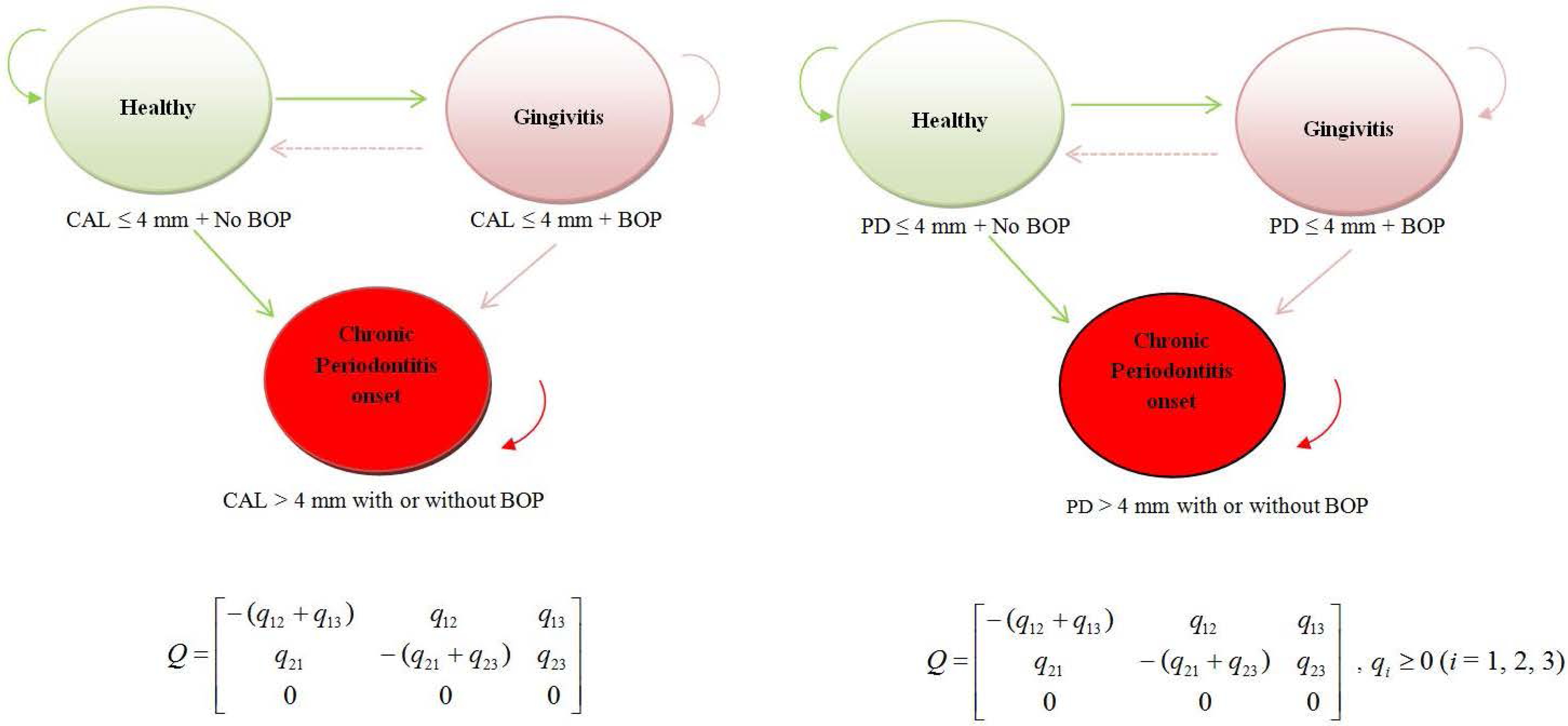
A general multi-state Markov model for gingivitis and chronic periodontitis onset based on CAL + BOP (left panel) and PD + BOP (right panel) classifications. States 1, 2 and 3 correspond to health, gingivitis and chronic periodontitis and possible transitions are represented by arrows. Sites can advance from a healthy state to a gingivitis state, and optionally recover from gingivitis to healthy. Because data were observed at arbitrary time points, direct transitions from health to chronic periodontitis are also permissible. However, sites that advance to chronic periodontitis (absorption state) are not expected to recover (transit to healthy state) or transit to gingivitis state. Q is the transition intensity matrix. For example, q₁₂ represents the instantaneous risk of moving from state 1 to state 2. Because transitions 3 → 1 and 3 → 2 are not permissible, q₃₁ = q₃₂ = q₃₃ = 0 .

The following transitions were allowed; a healthy site can either advance to gingivitis (slow progression) or advance directly to chronic periodontitis (fast progression). The fast progression transition was added to provide information on “bursting behavior” and in the present context it implies that a healthy site progresses to chronic periodontitis within half a year. In reality, sites undergoing this fast decay would have passed through the gingivitis state, although this state would not have been observed. A site with gingivitis can either transit to a health state (recovery) or advance to chronic periodontitis. Transitions from chronic periodontitis to health and gingivitis were considered not permissible.

Multi-state Markov model

We used a continuous Markov model with constant transition rates to represent periodontal disease progression in healthy sites. Chronic periodontitis is an absorbing state because transitions out of this state are not allowed. Hence we focused on the first occurrence of chronic periodontitis (“first hitting time”) and ignored further potential recovery due to the short duration of the study. Health and gingivitis are transient states as shown in Fig. 1 with arrows indicating allowed transitions between states. A transition probability satisfies the Markov property if future transitions depend on the present disease state of a site only, and not on how long the site has been in a given state or from where it has arrived. For example, if a site has gingivitis, then any future movement will only depend on the current state (gingivitis) while being independent of its previous history.

Our longitudinal data consisted of observations of the disease process at arbitrary times. The exact times at which state transitions occurred were not known although the underlying process evolved continuously in time. Kalbfleisch & Lawless (1985) introduced the analysis of panel data under a Markov assumption where movements between disease states are governed by transitional intensities q_rs(t, x(t)) with r,s = 1, 2, 3 (the three possible states) and depend on time t and individual level or time-dependent explanatory variables at time t, denoted x(t). In our case, the q_rs forms a (3 × 3)matrix Q whose rows sum to zero so that the diagonal entries are defined byq_rs = −Σ_s≠r q_rs . Since it is not possible to move from S₃(t) to either S₁(t) or S₂(t), then in the transition intensity matrix q₃₁ = q₃₂ = q₃₃ = 0 . The transition intensity matrix Q has the form given in Fig. 1.

We were also interested in the transition probabilities. We estimated the transition probabilities based on the observed transition rates using the method of maximum likelihood. In the case where Q is constant over time, the transition probability matrix P(t) = Exp (tQ). The full likelihood is then the product of probabilities of transition between observed states, over all sites and observation times, which is maximized in terms of log(q_rs ) (Jackson 2011).

Misclassification models

Several factors affect the variability and measurement accuracy of CAL and PD including periodontal disease progression and placement of site and tooth, and errors inherent to the experience and number of examiners and the choice of probe instruments (Holtfreter 2012). Clinical measurement errors may cause the observed disease states to be different from the true underlying disease status. To account for such misclassification, we extended the basic models allowing for misclassification using hidden multi-state Markov models (HMMs). The models and the results are presented in the supplementary information.

Regression model for covariates

We estimated the effects of measured covariates on the transition intensities q_rs in the Markov model using a proportional intensity model (Kalbfleisch & Lawless 1985). Suppose that each site has an associated vector of covariates x and that the process is time-homogeneous Markov with transition intensity matrix Q(x) , which depends on a covariate vector x. Then for each entry of Q(x), the transition intensity for site i at observation time J is q_rs(x_ij) = q⁽⁰⁾_rs exp(β ^T_rsx_ij ) where β_rs is a vector of regression parameters.

Model selection and assessment

A likelihood ratio test (LRT) statistic was used to compare nested models. This test produces a chi-square (χ²) value and a p-value. If two nested models are compared and the LRT produces p ≤ 0.05 , then the model being compared to fits the data better than the base model. We assessed the goodness of fit of our models by comparing the observed and expected prevalences under the model at a series of time points (Figs. S1 and S2).

Testing for time inhomogeneity

The LRT statistic was also used to test for time-inhomogeneity of the models. However, due to the short duration of the study, we observed very few transitions between gingivitis and periodontitis. This made the model estimation unstable, hence we present results from time homogeneous models.

Accounting for dependences

To account for dependencies between site observations in the same individual, we present confidence intervals of both the intensity matrix and transition probabilities obtained from bootstrapping at site level (1,000 bootstrap samples). All analyses were performed by using the msm package in R (Jackson 2011).

Results

Models based on CAL + BOP

During the 2-year time interval (between 6 months and 30 months), a total of 327 sites progressed from healthy state to gingivitis and 89 sites experienced rapid progression from healthy state to chronic periodontitis. There were also 182 transitions from gingivitis to health and 12 transitions from gingivitis to chronic periodontitis.

Gingivitis and chronic periodontitis onset - The null model

Table 1 shows the transition intensities for the null model (model without adjusting covariates). The estimated mean sojourn time for a healthy site was –1/ q₁₁ = –1/(–0.37) = 2.7 years [95% CI. 2.4 years, 3.0 years]. The average time spent in the gingivitis state was –1/q₂₂ = –1/(–2.06) = 0.5 years [95% CI. 0.4, 0.6]. The probabilities of a transition from a healthy state to either gingivitis or chronic periodontitis were q₁₂ /(q₁₂ + q₁₃) = 87% [95% CI. 86%, 88%] and q₁₃ /(q₁₂ + q₁₃) = 13% [95% CI. 12%, 14%] respectively. Similarly, the probability that the next disease state would be either health or chronic periodontitis for a site with gingivitis was 96% [95% CI. 94%, 98%] and 4% [95% CI. 2%, 6%] respectively.

Table 1.

Transition intensities for the CAL + BOP and PD + BOP models. Because transitions chronic periodontitis → health and chronic periodontitis → gingivitis were not permissible, then q₃₁ = q₃₂ = q₃₃ = 0. An average of −1/ (−0.37) = 2.70 years (32.4 months) is spent disease- free before a transition is made from the healthy state and an average of −1/ (−2.06) = 0.49 years (5.8 months) is spent with gingivitis before a transition is observed. In the PD + BOP model, an average of 1/0.37 = 2.70 years (32.4 months) is spent disease-free before a transition is observed and an average of 1/2.56 = 0.39 years (4.7 months) is spent with gingivitis before a transition is observed.

	CAL + BOP model			PD + BOP model
	Health	Gingivitis	Chronic Periodontitis	Health	Gingivitis	Chronic Periodontitis
Health	−0.37 (−0.42, −0.33)	0.32 (0.28, 0.37)	0.05 (0.04, 0.06)	−0.37 (−0.43, −0.33)	0.37 (0.32, 0.42)	0.01 (0.01, 0.02)
Gingivitis	1.97 (1.66, 2.31)	−2.06 (−2.42, −1.75)	0.09 (0.03, 0.16)	2.50 (2.17, 2.91)	−2.56 (−3.00, −2.22)	0.06 (0.02, 0.12)
Chronic Periodontitis	0	0	0	0	0	0

The corresponding 1-year and 2-year transition probabilities are summarized in Table 2 and plotted in Fig. 2. The system dynamics is characterized by a loss of healthy sites and a steady increase in the fraction of sites that have developed chronic periodontitis. The model estimates that approximately 5% and 10% of the healthy sites will have developed chronic periodontitis in 1 and 2 years, respectively. After an initial transient period, the density of sites in the gingivitis state stabilizes at 11 - 12%. Our model assessment (Fig. S1) revealed a tendency for the model to overestimate the proportion of sites in the healthy state, while underestimating the proportion with chronic periodontitis after 2 years.

Table 2.

Estimates of transition probabilities and 95% CI for sites that were healthy at 6 months based on CAL + BOP and PD + BOP classifications. States 1, 2 and 3 correspond to health, gingivitis and chronic periodontitis respectively. There was a 12% chance that a site that was healthy would convert to gingivitis (1 → 2) in the first 2 years for both CAL + BOP and PD + BOP classified models. The probabilities for progression to chronic periodontitis from healthy (1 →3) were at least three times higher for the CAL + BOP model compared to the PD + CAL model. After 2 years, recovery from gingivitis (2 → 1) was estimated as 75% for the CAL + BOP model and 83% for the PD + BOP model. Transitions 3 → 1 and 3 → 2 were not permissible.

	Predicted transition probabilities for sites that were healthy at 6 months
State transitions	CAL + BOP classified model		PD + BOP classified model
	Year 1	Year 2	Year 1	Year 2
1 → 2	0.12 (0.11,0.13)	0.12 (0.11,0.14)	0.12 (0.11,0.13)	0.12 (0.11,0.13)
1 → 3	0.05 (0.04, 0.06)	0.10 (0.08, 0.12)	0.01 (0.01,0.02)	0.03 (0.02, 0.04)
2 → 1	0.72 (0.68, 0.77)	0.75 (0.72, 0.78)	0.80 (0.77, 0.83)	0.83 (0.80, 0.85)
2 → 3	0.07 (0.04, 0.10)	0.12 (0.09, 0.15)	0.03 (0.01,0.05)	0.05 (0.02, 0.08)

Fig. 2.

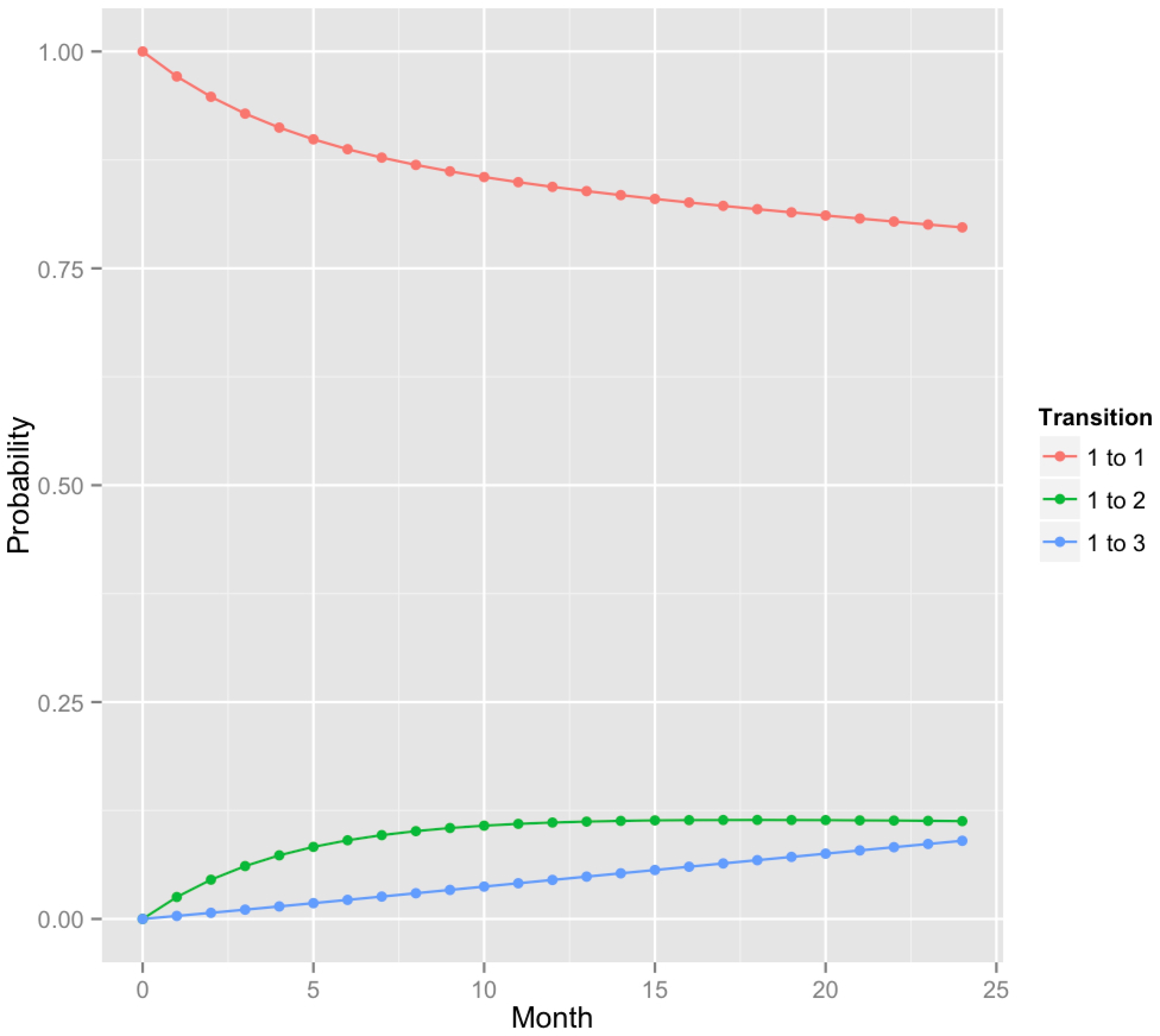
A plot of predicted transition probabilities for sites that were healthy at 6 months based on CAL + BOP classification. Here, states 1, 2 and 3 correspond to healthy, gingivitis and chronic periodontitis. Transition probabilities (1 → 3) were higher than for PD + BOP (see Fig. 3).

Models with adjusting covariates

The results of the univariate analyses for gingival redness, accumulation of plaque, age, smoking status, disease severity, gender and nationality are given in Table S1. A hazard ratio above one signifies a positive association between the covariate and the rate of transition. Conversely, a hazard ratio below one indicates a negative association between a covariate and the rate of transition. A hazard ratio equal to one implies no effect. All covariates were found to have a significant effect on one or more transitions. For example, accumulation of plaque significantly increased the transition intensity between health and gingivitis with a hazard ratio of 1.92 [95% CI. 1.41, 2.61].

The estimates from the final multivariate model show that disease severity was associated with a 7% and 15% increase per site with CAL > 4 mm at baseline in the risk for fast progression and progression from gingivitis to chronic periodontitis, respectively (Table 3). Smoking was associated with fast progression from health to chronic periodontitis with a hazard ratio of 2.11. Gingival redness and being male were associated with increased risks of transition from health to gingivitis by factors of 2.15 and 1.51 respectively. With age, the risk for transiting from health to gingivitis decreased by 3%.

Table 3.

Hazard ratios from the multivariate analysis of the CAL + BOP model given in Fig. 1. The likelihood ratio test was used to select this model. The risk for gingivitis onset was 51% higher in males than females while each year increase in age was associated with a 3% decrease in the risk of gingivitis onset.

	Hazard ratios and 95 % CI
Covariates	Health → Gingivitis	Health → Chronic periodontitis	Gingivitis → Health	Gingivitis → Chronic periodontitis
Gingival redness	2.15 (1.56, 2.98)*	0.48 (0.14, 1.70)	0.96 (0.64, 1.45)	3.11 (0.53, 18.34)
Smoking	0.72 (0.53, 1.00)	2.11 (1.19, 3.76)*	0.71 (0.48, 1.05)	1.02 (0.26, 3.97)
Gender: males	1.51 (1.10, 2.08)*	1.18 (0.67, 2.08)	1.22 (0.81, 1.84)	3.10 (0.84, 11.40)
Age	0.97 (0.96, 0.99)*	1.00 (0.97, 1.03)	0.98 (0.97, 1.00)	0.94 (0.87, 1.00)
Severity†	1.00 (0.97, 1.02)	1.07 (1.02, 1.12)*	1.00 (0.97, 1.04)	1.15 (1.06, 1.26)*

^†We estimated the severity of the disease in a subject at baseline by counting the number of teeth with CAL > 4 mm

^*Significant results at α = 0.05

Models based on PD + BOP

A total of 391 sites progressed from healthy state to gingivitis and 26 sites experienced rapid progression from healthy state to chronic periodontitis. There were also 227 transitions from gingivitis to health while only 7 transitions were observed from gingivitis to chronic periodontitis.

Gingivitis and chronic periodontitis onset - The null model

The transition intensities for the PD + BOP model without covariates are given in Table 1. The estimated mean sojourn time for a healthy site was 2.7 years [95% CI. 2.3years, 3.0 years] while the average time spent in the gingivitis state was 0.4 years [95% CI 0.3 years, 0.5 years]. The probabilities for a transition from a healthy state to either gingivitis or chronic periodontitis were 97% [95% CI. 95%, 98%] and 3% [95% CI. 2%, 5%] respectively. Similarly, the probability that the next disease state would be either health or chronic periodontitis for a site with gingivitis was 98% [95% CI.96%, 99%] and 2% [95% CI. 1%, 4%] respectively.

The time-dependent transition probabilities for this model are given in Table 2 and plotted in Fig. 3. Similar to the CAL + BOP model, the system dynamics is characterized by an ongoing loss of healthy sites and an increase in the proportion of sites that have developed chronic periodontitis. The model estimates that 1% and 3% of the healthy sites will develop chronic periodontitis in 1 and 2 years respectively. After an initial transient period, the density of sites in the gingivitis state stabilizes at 11 - 12%. We found a good correspondence between the observed and fitted model (Fig. S2).

Fig. 3.

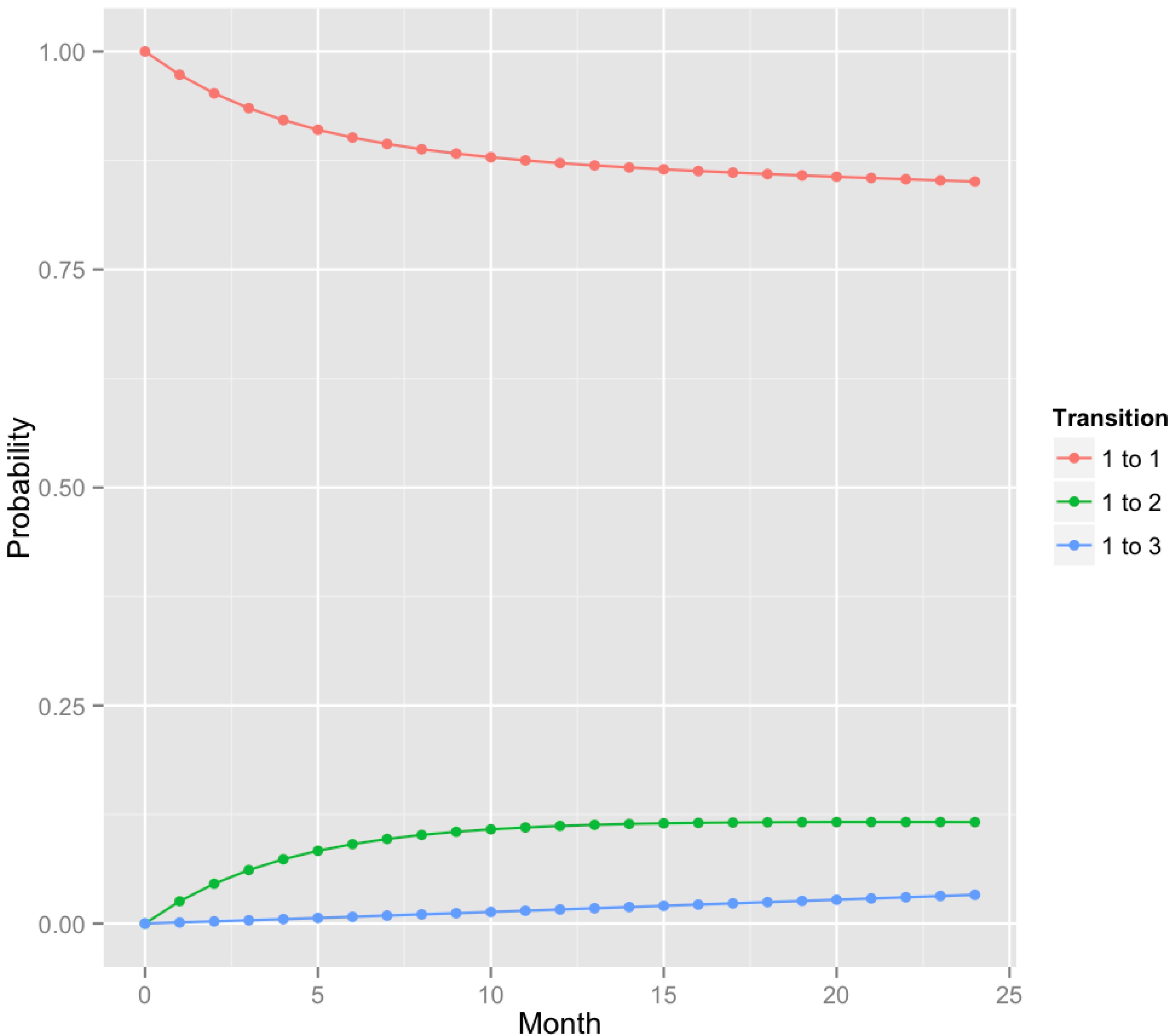
A plot of predicted transition probabilities for sites that were healthy at 6 months based on PD + BOP classification. Here, states 1, 2 and 3 correspond to health, gingivitis and chronic periodontitis. Estimates for transition probabilities (1 → 3) were lower than for CAL + BOP (see Fig. 2).

Models with adjusting covariates

Table S2 shows hazard ratios from the univariate analysis. For each site with severe chronic periodontitis at baseline, the risk for a healthy site to develop chronic periodontitis increased by 14% while accumulation of plaque was associated with a 71% increase in the hazard of gingivitis onset.

In our final five-parameter model, the risk for a healthy site to experience fast progression or progression from gingivitis to chronic periodontitis increased by 11% and 12% respectively for each site with PD > 4mm at baseline (Table 4). Fast progression to chronic periodontitis was 2.11 times more likely among smokers than non-smokers. Gingival redness increased the risk for transition from health to gingivitis by a factor of 2.13 and fast progression to chronic periodontitis by a factor of 3.43. Males were more likely to develop gingivitis than females with an increased risk of 39%. Each year increase in age was associated with a 2% decrease in the risk of progression from health to gingivitis.

Table 4.

Hazard ratios from the multivariate analysis of the PD + BOP model given in Fig. 2. Severity of disease at baseline was associated with an 11% increase in the hazard of chronic periodontitis onset from health state while each year increase in age was associated with 2% decrease in the hazard of gingivitis onset.

Hazard ratios (95 % CI)
Covariates	Health → Gingivitis	Health → Chronic periodontitis	Gingivitis → Health	Gingivitis → Chronic periodontitis
Gingival redness	2.13 (1.53, 2.97)*	3.43 (1.12, 10.52)*	1.13 (0.76, 1.68)	1.57 (0.38, 6.51)
Smoking	0.89 (0.66, 1.22)	2.20 (1.66, 7.37)*	1.02 (0.71, 1.45)	0.48 (0.05, 5.02)
Gender: males	1.39 (1.01, 1.91)*	0.77 (0.25, 2.39)	1.00 (0.68, 1.48)	7.43 (0.35, 15.63)
Age	0.98 (0.96, 0.99)*	1.00 (0.94, 1.06)	1.00 (0.98, 1.01)	0.88 (0.77, 1.02)
Severity†	0.96 (0.93, 1.00)	1.11 (1.00, 1.25)*	0.96 (0.92, 1.01)	1.12 (1.01 1.28)*

^†We estimated the severity of the disease in a subject at baseline by counting the number of teeth with PD > 4 mm

^*Significant results at a = 0.05

Misclassification model results

Results for the multivariate hidden Markov models (HMMs) and the full models without misclassifications were comparatively similar with respect to the estimated mean sojourn time for health and gingivitis (Table Suppl. 1), and the 2-year probability for transition (Table Suppl. 2), except for a lower estimate of the transition between health/gingivitis and chronic periodontitis in the PD + BOP model. However, in all HMMs, the misclassification probabilities between chronic periodontitis and health/gingivitis could not be estimated with precision (Table Suppl 3).

Discussion

The present study is the first attempt to estimate disease progression of healthy sites in susceptible patients with chronic periodontitis using multi-state Markov models.

Healthy sites in this group of patients experienced periodontal disease progression after an average of 2.7 years in both models. Overall, the majority of disease transitions in healthy sites were to the gingivitis state. This lesion recovered with a high probability after a mean duration of less than 6 months. Hence, our analyses suggest that the development of chronic periodontitis is commonly preceded by several instances of gingivitis followed by recession to a healthy state.

Comparison of the two models reveals two important differences. First, the CAL + BOP model predicted higher probabilities for fast progression and progression from gingivitis compared to the PD + BOP model. In consequence, roughly 1 in 10 (CAL + BOP) and 1 in 33 (PD + BOP) of healthy sites progressed to chronic periodontitis in 2 years. The fact that we obtained higher levels of chronic periodontitis in the CAL model is in agreement with Page & Eke (2007) who argued that using CAL alone would tend to overestimate periodontitis prevalence since attachment loss can be due to non-inflammatory causes. Instead, using PD alone would tend to underestimate disease prevalence because gingival recession, which is common from middle age, reduces PD. Second, we found gingival redness to be associated with fast progression in the PD + BOP model only. CAL and PD measurements provide different information about disease epidemiology. CAL is an indicator of cumulative tissue destruction, including past periodontal disease, while PD is an indicator of current disease status (inflammation) (Burt et al. 2005). Since gingival redness is an indicator of inflammation, this could explain why it exclusively predicted fast progression in the PD + BOP model.

One interesting finding in the present analyses is that with age, progression from health to gingivitis decreased. This result is in contrast with findings in previous Markov modeling studies of periodontitis, where the effect of age was recognized as reducing disease regression, rather than reducing disease progression (Faddy et al. 2000, Schätzle et al. 2009). There are numerous studies supporting that both prevalence and severity of periodontal disease increase with higher age. However, this relationship may not be related to age per se, but instead it may represent the outcome of prolonged exposure to true risk factors (Papapanou et al. 1991). The present study population had manifest periodontal disease. One could therefore speculate that the protective effect of age could be a “frailty effect”, where sites that are highly prone to develop periodontal disease, would manifest disease at an earlier age, so that healthy sites in subjects of higher age will tend to be more robust towards disease progression.

Disease severity is commonly included in risk assessment models for periodontitis; usually the number of sites with PD > 5 mm and the number of missing teeth are used as measures of cumulative disease severity (Kye et al. 2012). We showed that disease severity, measured by the number of sites with chronic periodontitis (CAL/PD > 4 mm) at baseline, was associated with fast progression and progression from the gingivitis state. This finding supports the use of sites with elevated probing depths as a prognostic factor, and suggests that measurements of sites with CAL > 4 mm could serve a similar role in risk assessment.

Smoking increased the rate of fast progression, but had no significant effect on slow progression through the gingivitis state. The latter finding may possibly be explained by decreased likelihood for BOP and inflammatory response among smokers, attributable to alterations in the gingival microvasculature (Kumar & Faizuddin 2011). Interestingly, Faddy et al. (2000) found, using a 2-state Markov model, that smoking and age inhibit the healing process rather than promoting disease progression. In the CAL + BOP model, our results indicate a lower recovery rate from gingivitis among smokers although the effect was only marginally significant (Table 3).

Males were associated with increased progression from health to gingivitis. Men have been shown to exhibit more periodontal disease than women (Albandar 2002), and this has traditionally been attributed to better oral hygiene practices and more frequent visits to dentists among women (Borrell & Papapanou 2005), although the latter argument does not apply in the current context since all subjects were examined every 6 months. A review of gender differences in periodontal disease concludes that while men appear at greater risk for disease, they do not appear at higher risk for more rapid destruction than women. The finding in the present study that males were not associated with fast progression supports this.

Classification problems in periodontal studies are well documented in the literature. As discussed by Armitage (1999), classification systems provide a framework by which to scientifically study the etiology, pathogenesis and treatment of diseases in an orderly fashion. Our study did not attempt to introduce new classification systems for periodontal disease. Rather, we aimed at understanding disease progression; more specifically, the burst theory using the two well-known established clinical markers of periodontal disease: CAL and PD. Our classification systems based on CAL, PD and BOP could provide a basis for understanding disease progression in an easy orderly way.

An attempt was also made at fitting time-inhomogeneous models in which transition intensities vary over time intervals. Although we found evidence of time inhomogeneity, the lack of enough transitions between disease states due to short duration of the study, prevented us from fitting such models.

We performed additional analyses allowing for misclassification between health/gingivitis and chronic periodontitis using hidden multistate Markov models (HMMs) to account for inaccuracies in the measurement of clinical attachment levels and probing depths. In these models, however, the confidence intervals for the estimated misclassification probabilities between chronic periodontitis and health/gingivitis were very wide, which made it difficult to draw conclusions from these analyses. This problem may be related to the short duration of the study period and the few observations of transitions to the chronic periodontitis state. For this reason, we chose to present the results of the models without inclusion of measurement error. Still, the HMM models may hint at which covariate effects are robust. For the CAL + BOP model, the HMM models confirmed the general findings presented here, except that the effect of gender may be obscure (Table Suppl. 5), and smoking was found to prevent regression from the gingivitis state. For the PD + BOP model, the effects of gingival redness and severity on fast progression were not found robust (Table Suppl. 6). In addition, no general effect of smoking, or gender was obtained.

The study had other limitations. First, one main limitation of the present study was its short duration. Chronic periodontitis is a slowly progressing disease that usually takes several years to develop. Due to its short duration, we observed few events of chronic periodontitis onset and it is possible that these transitions occurred in particular frail sites, which may not be representative of the general long-term disease dynamics of healthy sites in this group of patients. However, we included the chronic periodontitis state because it is informative and provides novel insights about the “bursting behavior” (Socransky et al. 1984). Second, our data may not describe accurately the natural history of periodontal disease development because the teeth showing signs of disease activity were cleansed. Third, a possible limitation with the multi-state Markov approach when used in the msm package for R is that unexplained heterogeneity in transition intensities may not be accounted for (Jackson 2011). This could have been represented by random effects models, which are yet to be implemented in the msm package. However, we accounted for dependences between observations by estimating bootstrapped transition intensities and probabilities. Alternatively, multi-state models with random effects can be fitted to longitudinal data from a Bayesian perspective using Win BUGS (Lunn et al. 2000).

Clinical Relevance.

Scientific rationale for the study: This is the first attempt to estimate disease progression of healthy sites and regression of diseased sites using multi-state Markov modeling in patients with chronic periodontitis.

Principal findings: Transition probabilities for gingivitis and chronic periodontitis were higher with CAL + BOP than with PD + BOP. In 2 years, the transition probabilities for developing chronic periodontitis from health were estimated at 10% and 3% respectively. Disease severity at baseline and smoking were associated with fast progression from health to chronic periodontitis within 6 months. With age, the rate of disease progression to gingivitis decreased.

Practical implications: Rates of disease progression from health to chronic periodontitis are influenced by severity of disease at baseline and smoking.