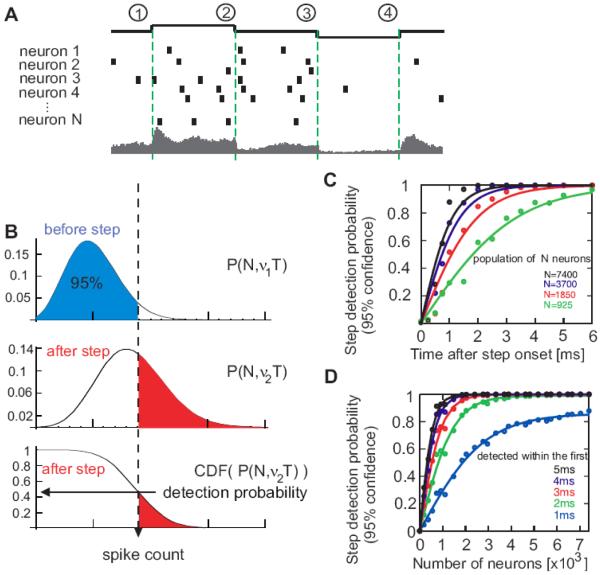
Figure 5.

Detection of population firing rate changes induced by changes of the mean input current (A) Illustration of step encoding in the population firing rate of N neurons. Top to bottom: timing of current steps; spike responses of neurons 1-N, with vertical bars representing individual spikes and the resulting peristimulus time histogram of the population firing rate (bottom, data from Figure 1E). (B) Illustration of a theoretical decoder. Binomial distributions P(N, ν₁T) of spike counts before the step, P(N, ν₂T) after the step and its cumulative distribution CDF(P(N, ν₂T)). Form the latter the probability that after-step spike count is outside the 95% boundary of the pre-step distribution is determined (hor izontal arrow). This corresponds to the probability of step detection with 95% confidence. (C,D) Probability of step detection vs. time after step onset (C) and number of neurons (C) as calculated from data in Figure 1C–F and averaged across conditions (1)–(4). Circles denote the data points and solid lines denote fits of the form f(T)=tanh(bT) or f(N)=a tanh(bN), respectively. Note that a popula tion of 7400 neurons (equiv. to the number of realizations) can detect 88% of steps within the first 1ms.