Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2016 May 23.
Published in final edited form as: Am Stat. 2016 Mar 31;70(1):33–38. doi: 10.1080/00031305.2015.1069760

The P-value you can't buy

Eugene Demidenko *
PMCID: PMC4867863  NIHMSID: NIHMS770470  PMID: 27226647

Abstract

There is growing frustration with the concept of the P-value. Besides having an ambiguous interpretation, the P-value can be made as small as desired by increasing the sample size, n. The P-value is outdated and does not make sense with big data: Everything becomes statistically significant. The root of the problem with the P-value is in the mean comparison. We argue that statistical uncertainty should be measured on the individual, not the group, level. Consequently, standard deviation (SD), not standard error (SE), error bars should be used to graphically present the data on two groups. We introduce a new measure based on the discrimination of individuals/objects from two groups, and call it the D-value. The D-value can be viewed as the n-of-1 P-value because it is computed in the same way as p while letting n equal 1. We show how the D-value is related to discrimination probability and the area under the receiver operating characteristic (ROC) curve. The D-value has a clear interpretation as the proportion of patients who get worse after the treatment, and as such facilitates to weigh up the likelihood of events under different scenarios.

Keywords: Discrimination error, Effect size, ROC curve, Significance testing

The P-value and its criticism

The P-value and the associated concept of statistical significance are at the heart of statistics as the empirical-evidence science. Although concerns regarding the abuse of this concept have been expressed in the past (e.g. Cohen 1994; Gelman and Stern 2006; Pharoah 2007), voices against the P-value have become louder and louder recently (Greenland and Poole 2013; Nuzzo 2013; Gelman 2013; Harvey, 2014). Recent discussions reached a culminating point when the journal Basic and Advanced Social Psychology published an editorial banning P-values (Trafimow and Marks 2015); see also Editorial, Signficance 12, 2015 for a discussion. We are not going to repeat the arguments against the P-value and its current use in applied statistics. Instead we emphasize another negative feature of the P-value and offer a solution. In short, we suggest using the effect size, as many statisticians already do, but expressed on the probability scale. The new concept, called the D-value, is in fact the probability of false discrimination and is equal to the area under the ROC curve.

You can make the P-value as small as you can afford

The little-known fact among nonstatisticians is that, with a large enough sample, n, the null hypothesis will always be rejected. This fact stems from the consistency of the test: With the sample size increasing to infinity, the power of the test approaches 1 even for alternatives very close to the null. In other words, with a large enough sample, the null hypothesis willalways be rejected regardless of the Type I error, α. What kind of knowledge does statistical hypothesis testing give if it leads to only one answer, “Reject the null hypothesis”?

Consider the following two examples. In the first example, we are concerned with testing a new antiobesity drug. Let a randomized trial involve n obese people in each placebo and drug groups. The null hypothesis is that the new drug has no effect with the alternative that the drug reduces weight (one-sided test). If x̄ and ȳ are the averages of weight in the placebo and drug groups, we compute the Z-score,

Z=y¯−x¯s2n, (1)

where s is the standard deviation (SD) estimate of the weight distribution in the two groups. To be specific, let n = 10, 000 obese people have been recruited in each group with average weighs x̄ = 249 lbs and ȳ = 250 lbs in the placebo and drug groups, respectively, with SD = s = 20 lbs. Plug these numbers into formula (1), get Z = 3.54, and compute the one-sided P-value using the formula

p=Φ(y¯−x¯s2n), (2)

where Φ is the cumulative distribution function (cdf) of the standard normal distribution, that yields the p-value, p = Φ(−3.54) = 0.0002. Does it mean that the drug should be recommended for use even though the difference in the average weight was 1 lb? Although the P-value is very small (statistics is all right), I doubt that anybody would buy this drug. Why did such a small difference between groups yield such a small P-value? The answer is the large n = 10,000, the sample size. Regardless of the difference x̄ − ȳ > 0 the P-value can be small enough with large n. It means that anything can be statistically significant—just use n large enough.

In the second example, the situation is quite different: A cancer researcher developed a new anticancer treatment and tries to demonstrate that it improves survival using n = 7 mice in the control and treatment groups. Let the median survival in control and treatment groups be 10 and 15 days, respectively, with SD = 6 days. Again, using formula (1), we compute Z = 1.56 with the P-value = 0.06. (A more appropriate test for survival comparison is the log-rank test (Rosner 2011), but it does not solve the principal problem.) Advice from a statistician: buy more mice. If the number of mice in each group is doubled (n = 14), the P-value = 0.014: the paper is published and a new grant is funded.

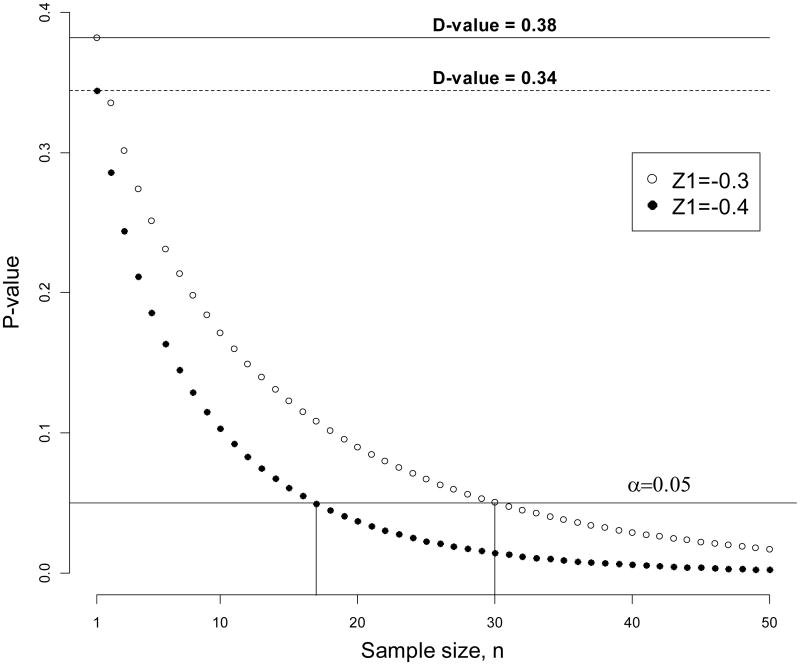
The sample size, n, has a direct impact on the P-value: Even if the difference in the group means is very small, with large n, the absolute value of the test statistic (1) can be made as large as you want, and consequently the P-value can be made as small as you want. This is illustrated in Figure 1, where the P-value as a function of n is shown for two values of (1) evaluated at n = 1: Z1 = −0.3 and Z2 = −0.4. For n = 10, both p-values > 0.05 (the difference between groups is not statistically significant). For Z1= −0.3, the difference between groups becomes statistically significant starting from n > 30, and for Z2= −0.4 the difference becomes statistically significant starting from n > 18.

Figure 1.

Figure 1

Open in a new tab

One may get the P-value as small as he/she wants by using a sufficient sample size. In contrast, the D-value does not depend on the sample size.

The ability to make the P-value as small as you want by increasing the sample size leads to an enormous number of statistically significant publications—practically every paper claims a statistically significant finding, but the results often contradict each other (Siegfried 2010).

The D-value: Individual versus group comparison

The root of the problem with the P-value is the group mean comparison. Several authors have challenged the mean comparison from a biological perspective. For example, Gunawardena (2014) attributes the lack of understanding of biological processes to the fact that “the mean may not be representative of the distribution.” Altschuler and Wu (2010) urge moving from population averages to individual comparison when studying cell functions, metabolism, signaling, and other vital properties.

How to interpret the treatment effect measured as the difference between the placebo and drug groups? The question of interest is, how does the drug affect you? For example, in the antiobesity drug example above, does a P-value of 0.0002 indicate that you will benefit from the drug with high probability, say, 1 − 0.0002? Statistical comparison would be useful if we could provide the risk–benefit analysis of the treatment effect based on the individual, not group, assessment. We do not treat a group, we treat an individual!

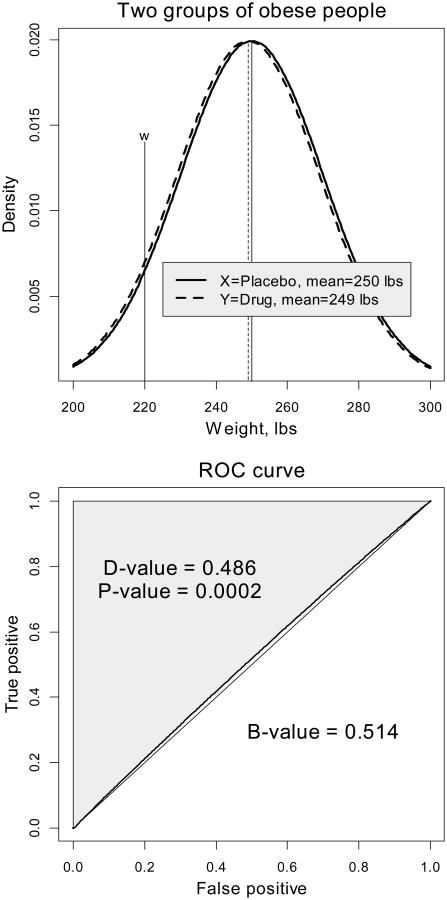
To assess the risk and benefit of the treatment, pick at random an individual from the placebo group with weight X and an individual from the drug group with weight Y; see Figure 2 for illustration, where two groups are represented by densities of the weight. The benefit of taking the drug is the probability that Y < X, or symbolically

Figure 2.

Figure 2

Open in a new tab

Computation of the D-value for the two-group comparison. Above: the density distributions for the two groups. Below: The ROC curve with the D-value. The 45° line corresponds to the random discrimination rule.

b=Pr(Y<X).

The risk (discrimination probability) of taking the drug is the complementary probability

δ=Pr(Y>X). (3)

We interpret δ as the probability that a randomly chosen person from the treatment group will be heavier than a randomly chosen person from the placebo group. Assuming that X and Y are from the normal population with means μx and μy and common variance σ2, it is easy to express the latter probability via the cumulative distribution function (cdf),

δ=Φ(μy−μxσ2) (4)

because X − Y is a normal random variable with mean μx − μy and variance 2σ2. Since μy < μx we have δ < 0.5. When the population means and the standard deviation (SD) are replaced with their estimates, we arrive at the empirical discrimination probability,

d=Φ(y¯−x¯s2), (5)

hereafter referred to as the D-value, an empirical version of the theoretical value (4) as an estimate of δ. The arguments of the normal cdf are referred to as the effect size (Field 2005; Ellis 2010; Sun et al. 2010).

The D-value is the probability that a randomly chosen person from the drug group is heavier than a randomly chosen person from the placebo group. The benefit of taking the antiobesity drug is the complementary probability

b=1−d,

the B-value. The D-value is closely related to the discrimination analysis and the ROC curve (Bamber 1975; Metz 1978); that is why we call it the “D-value.” Indeed, view the two populations of people, X and Y (depicted as solid and dashed lines, respectively, in the top panel of Figure 2), in terms of the discrimination based on the weight threshold, w. Then Y < w denotes the population of people who took the drug and weigh less than w, and X < w denotes the population of people who took the placebo and weigh less than w. The probability Pr(Y < w), the area under the density (dashed curve) to the left of w, is called the sensitivity, and the probability Pr(X < w), the area under the density (solid curve) to the left of w, is called false positive or 1–specificity. Since it is expected that people lose weight (μx < μy), we have Pr(Y < w) > Pr(X < w). The ROC curve is an implicitly defined function on the unit square, where the x-axis corresponds to Pr(X < w) and the y-axis corresponds to Pr(Y < w). Since the distributions are assumed normal, the ROC is called binormal (Demidenko 2012). Due to the latter inequality between probabilities, the ROC curve is above the 45° line. It is not difficult to prove (Demidenko 2013) that the area under the ROC curve is equal b = 1 − d and the area above the curve is equal d, where d is defined by equation (5).

In no way do we claim originality in proposing δ = Pr(Y > X) to measure the distance between two distributions. For example, Wolfe and Hogg (1971) advocated (4) as the measure of the difference between distribution locations and its association with the Mann-Whitney form of the Wilcoxon nonparametric statistic. Moreover, there exists a rich body of literature on statistical inference for Pr(Y > X), see Newcombe (2006a, 2006b) and Zhou (2008).

In summary, the proportion of cases in which the weight of a randomly chosen person from the placebo group is less than the weight of a randomly chosen person from the treatment group is equal to the area above the ROC curve and is equal to the D-value.

The connection between the P-value, the D-value, and effect size

The D-value is the n-of-1 P-value (Lillie et al. 2011; Joy et al. 2014). Indeed, compare the P-value formula (2) with the D-value formula (5). They are the same except for the presence of n in the former formula. Explicitly, if {Yi} and {Xj} are two random samples, we state,

P−value=Pr(Y¯>X¯),D−value=Pr(Yi>Xi).

The first probability expresses the difference between averages and the second probability expresses the probability on the individual level.

The connection between the P-value, the effect size and Pr(Y > X) was only recently mentioned in a short and fairly technical statistical paper by Browne (2010) that went practically unnoticed. Here, we make the exposition much clearer with emphasis on the interpretation:

D−value=effect size on the probability scale.

Although the effect size, like as the D-value, does not decrease with the sample size, its interpretation is not clear, as was indicated by Wolfe and Hogg (1971) almost 50 years ago. On the other hand, the D-value is easy to interpret: For example, a widely used effect size of 0.5 means that the proportion of treated patients who do not improve will be roughly 30% and the proportion who do improve will be 70% (D-value = Φ(−0.5) ⋍ 0.3). Expressing the treatment effect using probability could be especially important for probabilistic comparison when effect size is just not available. For example, consider a typical situation when weighing the pros and cons of a new drug with the D-value = 0.3 for an elderly patient whose chance of survival within 5 years, even if the drug would help, is 1 out of 5. Then the actual benefit of the new drug will be only 0.7 × 0.2 = 0.14. Certainly, doctors consider the age of the patient before prescribing a new drug, but the D-value facilitates quantitative assessment of the benefits on the probability scale.

The D-value is for personalized medicine when the treatment is sought, not on a group, but on an individual level. Personalized medicine is a growing approach for treating patients on the individual level, sometimes regarded as the future of medicine. The P-value is just the wrong quantity to characterize the efficacy of such studies.

SD, not SE

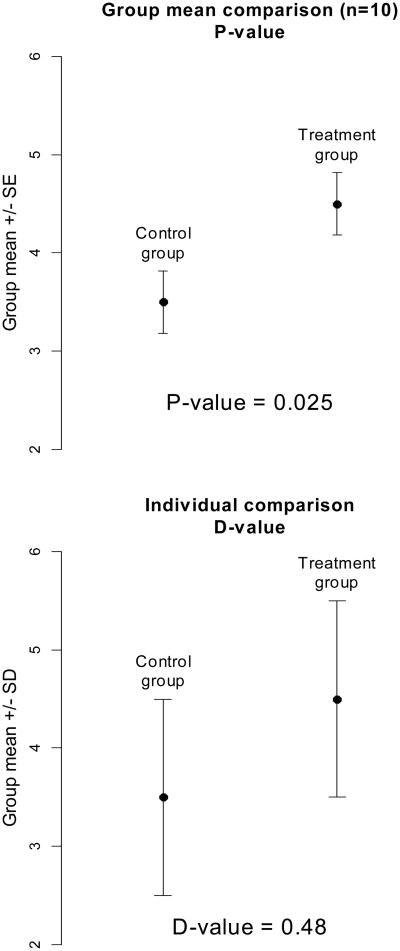
As was stated earlier, the root of the problem with the P-value is that it compares averages. Since the standard error (SE) of the mean is SD/√n, SE may be as small as desired if the sample size, n, is large enough. When the data are presented graphically as means ± SE, the individual variation is reduced by a factor of the square root of n. We suggest Figure 3 to illustrate. In the top plot, the SE error bars create an illusion of a satisfactory separation with the statistically significant P-value = 0.025. In the bottom plot, the same data are shown with SD error bars and the D-value = 0.48. Only 52% of individuals benefit from the treatment.

Figure 3.

Figure 3

Open in a new tab

SD or SE? Typical group mean comparison and data visualization. Showing SE suggests good group separation (the data in both plots are the same).

Showing SE error bars silently assumes application of the P-value for group comparison, showing SD error bars assumes the D-value for individual comparison. Since we advocate for the D-value, we urge using the SD, not SE, error bars. In short, the P- and D-values are computed in the same way but the former uses SE and the latter uses SD.

The D-value for linear regression

The arguments against the traditional P-value in a two-group comparison can be generalized to the linear regression model

yi=α+βxi+εi,i=1,2,…,n,

where yi is the dependent variable, xi is the associated factor/predictor of the ith subject or measurement, and εi is the normally distributed random error term. The P-value for the slope, β, can be made arbitrarily small by increasing the number of observations, n. This phenomenon is well known to health economics researchers who work with Medicare data (n may be several thousands or millions, see an example below): Basically, any variable (x) is a statistically significant predictor of the treatment outcome (y).

The D-value for linear regression can easily be generalized by considering two populations of y corresponding to x and x + 1. Since the difference in the means is estimated as b, the slope of the least squares regression, the D-value, is defined as

d=Φ(|b|sn),

where s is the standard error of the slope from the regression estimation. Note that the traditional one-sided P-value is computed as

p=Φ(−|b|s),

which is n dependent because s approaches zero when n goes to infinity. Typically, the P-value is computed based on the t-distribution. Here, we use the normal distribution just for transparency of the presentation. As in the two-sample problem, the D-value may be viewed as the n-of-1 P-value. Indeed, as follows from the above formulas, P turns into D when n = 1. The D-value for the multivariate regression has the same interpretation as for a simple univariate regression; the only difference is that s is computed by a more complicated formula involving matrix inverse.

We illustrate the D-value with an example of predicting the travel time to the nearest cancer center for n = 47,383 breast cancer patients using Medicare data (Onega et al. 2008; Demidenko et al. 2012, Table 1). Stage has four categories and Surgery is a dichotomous variable. The P-values for all three factors are very small (the factors are statistically significant) and yet the n-independent coefficient of determination R2 = 0.0014: only 0.15% of travel time variation can be explained by these three factors. How is it possible? The answer is large n: Paradoxically, the regression may explain almost nothing and yet all predictors may be statistically significant. The D- and B-values do not necessarily increase or decrease with n and reflect the actual relationship between predictor and dependent variable, with a clear interpretation. For example, the probability that a woman with breast surgery spends more time for travelling to a cancer center compared to a woman with no surgery is 0.506. To compare the travel time for the patients of a ten-year age difference, we compute the D-value

Table 1.

Multivariate regression of the travel time (hours) to the nearest cancer center R2 = 0.0014, n = 47, 383.

Factor Coefficient SE P-value D-value B-value
Age (years) −0.0054 0.00075 6.6 × 10−13 0.487 0.513
Stage (0–4) 0.0098 0.00232 2.4 × 10−5 0.492 0.508
Surgery (0,1) 0.0720 0.02225 1.2 × 10−3 0.494 0.506
Open in a new tab
d=Φ(−0.0054×100.0007547383)=0.37.

This means that the probability that younger patients spend less time travelling than older patients is 0.37. We would like to note that the regression coefficients themselves also have a meaningful interpretation applied to an individual. For example, a woman with surgery spends 4.3 minutes more getting to a cancer center compared to a woman with no surgery. But such interpretation does not take into account the uncertainty of the coefficients, unlike the D-value which is expressed on the probability scale.

Conclusions

There is growing frustration with the concept of the P-value (Siegfried 2010; Adler 2014; Trafimow and Marks 2015). In addition to its ambiguous interpretation, the P-value can be made as small as desired using a large enough sample. The ability of getting P-values arbitrarily small with increased sample size contributes to false positive findings, usually referred to as publication bias, resulting in statistically significant reports sometimes contradicting each other (Alberts et al. 2014). Differences in sample sizes contribute to the nonrepro-ducibility of scientific studies: The same studies with different n yield different P-values. Therefore, some may be statistically significant and while others are not (Johnson 2013).

Classical statistics aims at testing the means of the distributions. The mean comparison is the root of the P-value problem. Several researchers urge studying phenomena on the distribution/individual level in biology, not on the mean level (Gunawardena 2014). Consequently, standard errors and standard error bars, when displaying group data, should be abandoned. Standard deviation bars should be shown instead because they tell how strongly the populations from two groups can be discriminated on the individual basis.

We suggest the D-value to report the results of the group comparison. The D-value is a missing dot connecting the P-value, effect size and discrimination error. One may view the D-value as the effect size expressed in terms of the probability of group separation; as such it has a clear interpretation. This value, unlike the P-value, does not have a tendency to increase or decrease with the sample size. The D-value also has a clear interpretation on the individual level and may be viewed as the n-of-1 P-value.

Simply put, the D-value is the proportion of patients who got worse after the treatment. The advantage of the D- and B-values, unlike the effect size, is that they are expressed on the probability scale and therefore can be further used to weigh up the likelihood of events under different scenarios.

In August of 2014 at the Boston Joint Statistical Meeting, Science Editor-in-Chief Marcia McNutt urged statisticians to investigate the poor reproducibility of scientific experiments and their respective statistical analyses (Significance 11, 2014, p. 4). It is no wonder that P-values and their respective “statistically significant” findings cannot be reproduced: They depend on the sample size. This paper offers the solution of replacing the P-value with the D-value. Of course, this change will not solve the problem of reproducibility in science, but it at least removes a strong bias toward large n.

Acknowledgments

I am thankful to the Associate Editor and two reviewers for their positive criticisms and comments that improved the paper. This work was supported by NIH grants P30 CA23108-21, P20 GM103534, UL1TR001086, P01ES022832, P20GM104416.

References

  1. Adler J. The reformation. Pacific Standard. 2014 May-Jun; Available online at http://www.psmag.com/navigation/health-and-behavior/can-social-scientists-save-themselves-human-behavior-78858/
  2. Alberts B, Kirschner MW, Tilghman S, Varmus H. Rescuing US biomedical research from its systemic flaws. PNAS. 2014 doi: 10.1073/pnas.1404402111. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Altschuler SJ, Wu LF. Cellular heterogeneity: Do differences make a difference? Cell. 2010;141:559–563. doi: 10.1016/j.cell.2010.04.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Bamber D. The area above the ordinal dominance graph and the area below the receiver operating characteristic graph. Journal of Mathematical Psychology. 1975;12:387–415. [Google Scholar]
  5. Browne RH. The t-test p value and its relationship to the effect size and P(X > Y) American Statistician. 2010;64:30–33. [Google Scholar]
  6. Cohen J. The Earth is round (p <.05) American Psychologist. 1994;49:997–1003. [Google Scholar]
  7. Demidenko E. Confidence intervals and bands for the binormal ROC curve revisited. Journal of Applied Statistics. 2012;39:67–79. doi: 10.1080/02664763.2011.578616. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Demidenko E. Mixed Models: Theory and Applications with R. 2nd. Hoboken: Wiley; 2013. [Google Scholar]
  9. Demidenko E, Sargent J, Onega T. Random effects coefficient of determination for mixed and meta-analysis models. Communications in Statistics—Theory and Methods. 2012;41:953–969. doi: 10.1080/03610926.2010.535631. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Editorial. Significance. 2015:6. [Google Scholar]
  11. Ellis PD. The Essential Guide to Effect Sizes. Cambridge: Cambridge University Press; 2010. [Google Scholar]
  12. Field A. Discovering Statistics Using SPSS. London: Sage; 2005. [Google Scholar]
  13. Pharoah P. How not to interpret a p-value? Journal of the National Cancer Institute. 2007;99:332–333. doi: 10.1093/jnci/djk061. [DOI] [PubMed] [Google Scholar]
  14. Gelman A. Commentary: P values and statistical practice. Epidemiology. 2013;24:69–72. doi: 10.1097/EDE.0b013e31827886f7. [DOI] [PubMed] [Google Scholar]
  15. Gelman A, Stern H. The difference between ‘significant’ and ‘not significant’ is not itself statistically significant. American Statistician. 2006;60:328–331. [Google Scholar]
  16. Greenland S, Poole C. Living with p values: Resurrecting a Bayesian perspective on frequentist statistics. Epidemiology. 2013;24:62–68. doi: 10.1097/EDE.0b013e3182785741. [DOI] [PubMed] [Google Scholar]
  17. Gunawardena J. Models in biology: Accurate descriptions of our pathetic thinking. BMC Biology. 2014;12:29. doi: 10.1186/1741-7007-12-29. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Harvey LA. Statistical power calculations reflect our love affair with p-values and hypothesis testing: Time for a fundamental change. Spinal Cord. 2014;52:2–2. doi: 10.1038/sc.2013.117. [DOI] [PubMed] [Google Scholar]
  19. Johnson VE. Revised standards for statistical evidence. PNAS. 2013;111:5773–5777. doi: 10.1073/pnas.1313476110. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Joy TR, Monjed A, Zou GY, Hegele RA, McDonald HG, Mahon JL. N-of-1 (single-patient) trials for statin-related myalgia. Annals of Internal Medicine. 2014;60:301–312. doi: 10.7326/M13-1921. [DOI] [PubMed] [Google Scholar]
  21. Lillie EO, Patay B, Diamant J, Issell B, Topol EJ, Schork NJ. The n-of-1 clinical trial: The ultimate strategy for individualizing medicine? Personalized Medicine. 2011;8:161–173. doi: 10.2217/pme.11.7. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Metz CE. Basic principles of ROC analysis. Seminars in Nuclear Medicine. 1978;8:283–298. doi: 10.1016/s0001-2998(78)80014-2. [DOI] [PubMed] [Google Scholar]
  23. Newcombe RG. Confidence intervals for an effect size measure based on the Mann—Whitney statistic. Part 1: General issues and tail-area-based methods. Statistics in Medicine. 2006a;25:543–557. doi: 10.1002/sim.2323. [DOI] [PubMed] [Google Scholar]
  24. Newcombe RG. Confidence intervals for an effect size measure based on the Mann—Whitney statistic. Part 2: Asymptotic methods and evaluation. Statistics in Medicine. 2006b;25:559–573. doi: 10.1002/sim.2324. [DOI] [PubMed] [Google Scholar]
  25. Nuzzo R. Statistical errors. Nature. 2013;506:150–152. doi: 10.1038/506150a. [DOI] [PubMed] [Google Scholar]
  26. Ocana A, Tannock IF. When are ‘positive’ clinical trials in oncology truly positive? Journal of the National Cancer Institute. 2011;103:16–20. doi: 10.1093/jnci/djq463. [DOI] [PubMed] [Google Scholar]
  27. Onega T, Duel EJ, Shi X, Wang D, Demidenko E, Goodman D. Geographic access to cancer care in the U.S. Cancer. 2008;138:1919–1933. doi: 10.1002/cncr.23229. [DOI] [PubMed] [Google Scholar]
  28. Rosner B. Fundamentals of Biostatistics. 7th. Boston: Brooks/Cole; 2011. [Google Scholar]
  29. Siegfried T. Odds are, it's wrong: Science fails to face the shortcomings of statistics. Science News. 2010;177:26. Available online at: https://www.sciencenews.org/article/odds-are-its-wrong. [Google Scholar]
  30. Sun S, Pan W, Wang LL. A comprehensive review of effect size reporting and interpreting practices in academic journals in education and psychology. Journal of Educational Psychology. 2010;102:989–1004. doi: 10.1037/a0019507. [DOI] [Google Scholar]
  31. Trafimow D, Marks M. Editorial. Basic and Social Psychology. 2015;37:1–2. [Google Scholar]
  32. Wolfe DA, Hogg RV. On constructing statistics and reporting data. American Statistician. 1971;25:27–30. [Google Scholar]
  33. Zhou W. Statistical inference for P(X<Y) Statistics in Medicine. 2008;27:257–279. doi: 10.1002/sim.2838. [DOI] [PubMed] [Google Scholar]

RESOURCES