Wall Mechanical Properties and Hemodynamics of Unruptured Intracranial Aneurysms

Abstract

Purpose

To investigate the relationship between the intra-aneurysmal hemodynamic conditions and the mechanical properties of the wall in human aneurysms.

Methods

A total of eight unruptured aneurysms were analyzed. Computational fluid dynamics (CFD) models were constructed from pre-operative 3D rotational angiography images. The aneurysms were clipped and the domes were resected and mechanically tested to failure with a uniaxial testing system under multi-photon microscopy. Linear regression analysis was performed to explore possible correlations between hemodynamic quantities and the failure characteristics and stiffness of the wall.

Results

The ultimate strain was negatively correlated to aneurysm inflow rate (p=0.021), mean velocity (p=0.025), and mean wall shear stress (p=0.039). It was also negatively correlated to inflow concentration, oscillatory shear index and measures of the complexity and instability of the flow; however these trends did not reach statistical significance. The wall stiffness at high strains was positively correlated to inflow rate (p=0.014), mean velocity (p=0.008), inflow concentration (p=0.04), flow instability (p=0.006), flow complexity (p=0.019), wall shear stress (p=0.002) and oscillatory shear index (p=0.004).

Conclusions

In a study of 8 unruptured intracranial aneurysms, ultimate strain is negatively correlated with aneurysm inflow rate, mean velocity and mean wall shear stress. Wall stiffness is positively correlated with aneurysm inflow rate, mean velocity, wall shear stress, flow complexity and stability, and oscillatory shear index. These trends and the impact of hemodynamics on wall structure and mechanical properties should be further investigated in larger studies.

INTRODUCTION

Understanding cerebral aneurysm pathogenesis is extremely important to improve aneurysm evaluation and patient management [1–3]. Numerous prior studies have identified many factors that potentially contribute to the development, enlargement and rupture of intracranial aneurysms [4]. However, the links between these factors and the underlying mechanisms responsible for the formation, growth and stabilization or rupture of cerebral aneurysms is still poorly understood [5, 6]. It is generally accepted that the evolution of cerebral aneurysms is driven by flow-induced progressive degradation of the wall [4, 7, 8]. It has been suggested that aberrant aneurysmal flow conditions cause endothelial dysfunction which induces accumulation of cytotoxic and pro-inflammatory substances in the wall as well as thrombus formation, that in turn result in loss of mural cells and wall degeneration [9, 10]. This conjecture is supported by histological analysis of resected human aneurysm tissue [8]. On the other hand, based on mechanical testing of tissue samples collected after aneurysm clipping, Costalat et al. conjectured mechanical stiffness of the aneurysm wall may be associated to rupture [11]. More recently, Robertson et al. [12] studied human aneurysm tissues using multi-photon microscopy and showed mechanical properties and collagen architecture can differ even among unruptured aneurysms. However, the connections between the hemodynamic environment within the aneurysm sac and the wall structure and mechanical behavior have not been studied.

The purpose of this work was to investigate possible associations between aneurysmal hemodynamics and mechanical properties of the wall of human intracranial aneurysms.

METHODS

Clinical, Image and Tissue Data

A total of 8 sufficiently large samples (larger than 4mm x 5mm) from a series of 15 harvested unruptured intracranial aneurysm domes in 46 consented patients undergoing elective surgical clipping were analyzed. Prior to intervention, aneurysms were imaged with 3D rotational angiography (3DRA). During the intervention, after placing the clip, the aneurysm dome was resected. Harvested tissue samples were placed in a prepared vial with 0.9% (w/v) saline solution and transported to the lab for analysis within 48 hours. Institutional review board (IRB) approval was obtained for patient consent, handling of patient data, tissue harvest, and analysis.

Wall Mechanical Testing

The samples were mechanically tested to failure using a custom designed uniaxial loading system compatible with a multi-photon microscope (UA-MPM) that allows simultaneous testing and structural imaging of tissue samples [13]. In particular, due to their capacity for second harmonic generation (SHG), collagen fibers can be imaged without staining and traditional destructive techniques. Collagen fibers in the samples were imaged from the luminal (medial) and abluminal (adventitial) sides using an Olympus FV1000 MPE (Tokyo, Japan) equipped with a Spectra-Physics DeepSee Mai Tai Ti-Sapphire laser (Mountain View, CA) with a 1.12NA 25x MPE water immersion objective at an excitation wavelength of 870nm. The SHG signal was collected using a 400nm emission filter with a ±50 spectral bin. All MPM images shown are in a 500μm x 500μm scale. For mechanical testing, rectangular strips of the aneurysm were cut in the meridional direction (samples from all aneurysms were cut to roughly the same size: 4mm x 7mm), gripped by mechanical clamps and placed in a bath of 0.9% (w/v) saline at room temperature in the UA-MPM system. Fine-grade sandpaper was adhered to the grips to avoid the need for adhesives [13]. Specimens were subjected to uniaxial extension at a speed of 20 μm/s controlled by a linear actuator (ANT-25LA, Aerotech, PA) and force was recorded with a 5lb load cell (MDB-5, Transducer Techniques, CA). Force vs. displacement curves were obtained after five cycles of preconditioning to 0.3N and used to calculate Cauchy stress as a function of strain. Strain was defined relative to the configuration of the tissue under 0.005N load. Further details of the tissue handling protocol, mechanical tests and MPM imaging can be found in a separate article [12].

Hemodynamics Modeling

Subject-specific computational fluid dynamics (CFD) models were constructed from pre-operative 3DRA images [14]. All aneurysms were located in the anterior circulation. All reconstructions included the internal carotid artery and were extended proximally as much as possible, to minimize the effect of inlet boundary conditions on aneurysm hemodynamics. Pulsatile flow conditions were derived from phase-contrast magnetic resonance measurements in normal subjects [15]. Flow waveforms were scaled with the inflow vessel cross-sectional area to achieve a mean wall shear stress of 15 dyne/cm² according to the principle of minimum work (Murray’s law) [16]. Vessel walls were assumed rigid and blood a Newtonian fluid with density ρ=1.0 g/cm³ and viscosity μ=0.04 Poise. The 3D incompressible Navier-Stokes equations were numerically solved with finite elements on unstructured grids with a resolution of 0.2 mm and a time step of 0.01 sec [14].

Data Analysis

A number of variables were computed from the CFD simulations to quantitatively characterize the aneurysm hemodynamic environment, including: a) aneurysm inflow rate (Q), b) aneurysm mean velocity (VE), c) inflow concentration index (ICI), d) POD entropy (podent) – a measure of stability of the intra-aneurysmal flow structure, e) vortex core-line length (corelen) – a measure of complexity of the intra-aneurysmal flow pattern, f) shear concentration index (SCI) a–measure of concentration of the wall shear stress distribution, g) mean wall shear stress (WSS), h) mean oscillatory shear index (OSI), and i) percent area under low wall shear stress relative to the parent vasculature (LSA). All quantities were calculated as spatial averages over the aneurysm cavity and time averages over the cardiac cycle. For precise mathematical definitions of these variables and detailed description of the methodology used to compute these quantities see [17, 18].

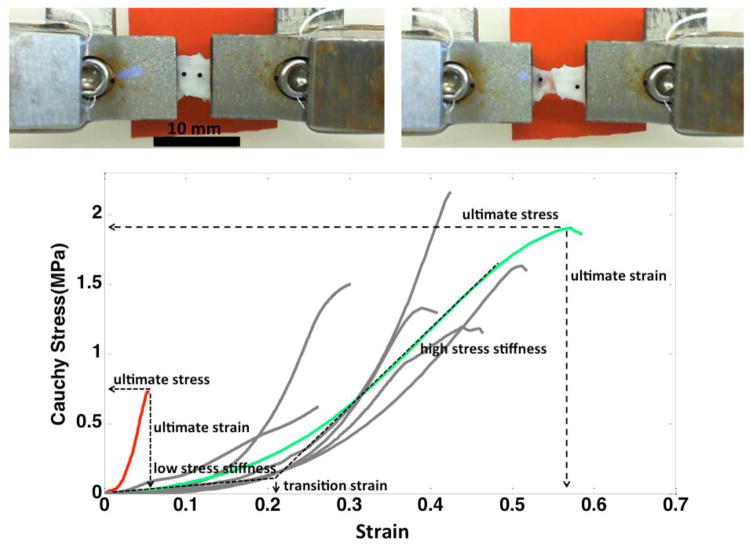
The stress and strain curves for the aneurysm wall, prior to failure is largely exponential in nature [12]. As such, the curves were classified into four regimes, listed in order of increasing load and shown in Figure 1: i) low stress region where the wall is highly elastic (toe region), ii) transition region, iii) high stress regime with a nearly linear response, followed by iv) sub-failure regime, marked by a decrease in slope of the stress strain curve ending with failure of the tissue. The mechanical response was characterized in terms of the following parameters: a) low stress stiffness - slope of a linear fit for the low stress region, b) high stress stiffness - slope of a linear fit for the high stress region, c) transition strain - strain at intersection of low and high stress stiffness lines, d) ultimate stress – maximum stress prior to failure, e) ultimate strain - the strain corresponding to ultimate stress, and f) ultimate tension (engineering) - product of ultimate stress (engineering) and unloaded thickness. The ultimate tension provides a measure of the ability of the wall to withstand loading. In contrast, the ultimate stress and strain are intrinsic material properties characterizing failure behavior. Linear regression analysis was performed to explore possible correlations between hemodynamic variables and wall mechanical properties. All correlations were carried out using the Python package SciPy.

Figure 1.

Stress-strain relationships (bottom). Examples of an aneurysm with stiff walls and low ultimate strain and stress (CA15), and an aneurysm with softer walls and greater ultimate stress and ultimate strain (CA26) have been highlighted in red and green, respectively. Top insert: picture of a sample with grips before stretching (left) and after it fails (right). Note that the tear occurs near the middle of the sample, not at the grips.

RESULTS

Mechanical behaviors of the aneurysms are presented in Table 1 and Figure 1, and their corresponding flow characteristics are given in Table 2. Correlations for both high stress stiffness and ultimate strain and hemodynamic variables reached statistical significance. Table 3 lists the slope of the linear regression, the correlation coefficient (R²) and the p-value of the correlation between each hemodynamic variable and the measured ultimate strain and high-strain stiffness. For p<0.05 the slope of the corresponding linear regression is significantly different from zero with a 95% confidence.

Table 1.

Material properties of harvested human aneurysm tissue samples.

ID	Thickness (mm)	Transition Strain	Low-Strain Stiffness (MPa)	High-Strain Stiffness (MPa)	Ultimate Strain	Ultimate Stress (MPa)	Ultimate Tension (Kg/s2)
CA1	0.24	0.16	0.35	12.24	0.30	1.50	285
CA11	0.21	0.11	1.66	2.93	0.26	0.63	105
CA12	0.20	0.28	0.58	14.09	0.42	2.16	320
CA15	0.13	0.02	2.35	24.41	0.05	0.73	90
CA25	0.24	0.26	0.24	6.18	0.51	1.63	280
CA26	0.45	0.22	0.90	5.43	0.57	1.90	580
CA39	0.21	0.24	0.34	6.38	0.44	1.20	183
CA46	0.30	0.24	0.22	9.11	0.38	1.34	300

Table 2.

Hemodynamic characteristics of cerebral aneurysms.

ID	Q (ml/s)	ICI	VE (cm/s)	podent	corelen (cm)	SCI	WSS (dyne/cm2)	OSI	LSA
CA1	1.52	2.00	9.53	0.31	2.86	4.39	19.57	0.019	49.3%
CA11	0.58	0.48	6.68	0.30	1.68	11.58	11.13	0.010	79.7%
CA12	0.71	0.65	10.18	0.62	2.84	6.00	25.30	0.025	75.5%
CA15	3.52	2.28	23.62	1.03	5.65	3.92	42.87	0.056	59.5%
CA25	0.09	0.21	0.98	0.36	0.30	21.70	1.31	0.020	97.1%
CA26	0.61	0.70	7.24	0.29	2.80	10.22	14.17	0.016	69.1%
CA39	0.99	0.85	8.55	0.17	3.02	4.23	14.38	0.007	40.2%
CA46	2.18	1.74	14.11	0.11	1.46	2.80	23.27	0.004	62.3%

Table 3.

Linear regression of hemodynamic variables against wall ultimate strain and material stiffness at high stress (past the toe region).

wall property	flow variable	slope	R2	p-value
ultimate strain	Q	−0.12	0.617	0.021*
	VE	−0.019	0.597	0.025*
	ICI	−0.14	0.474	0.059
	podent	−0.36	0.423	0.081
	corelen	−0.067	0.412	0.086
	SCI	0.011	0.186	0.287
	WSS	−0.010	0.535	0.039*
	OSI	−6.44	0.414	0.085
	LSA	0.24	0.069	0.531
material stiffness at high stress	Q	5.01	0.659	0.014*
	VE	1.20	0.717	0.008*
	ICI	6.44	0.531	0.040*
	podent	19.9	0.741	0.006*
	corelen	3.48	0.629	0.019*
	SCI	−0.52	0.227	0.232
	WSS	0.51	0.813	0.002*
	OSI	369.3	0.772	0.004*
	LSA	−0.101	0.065	0.53

^*Indicates statistically significant.

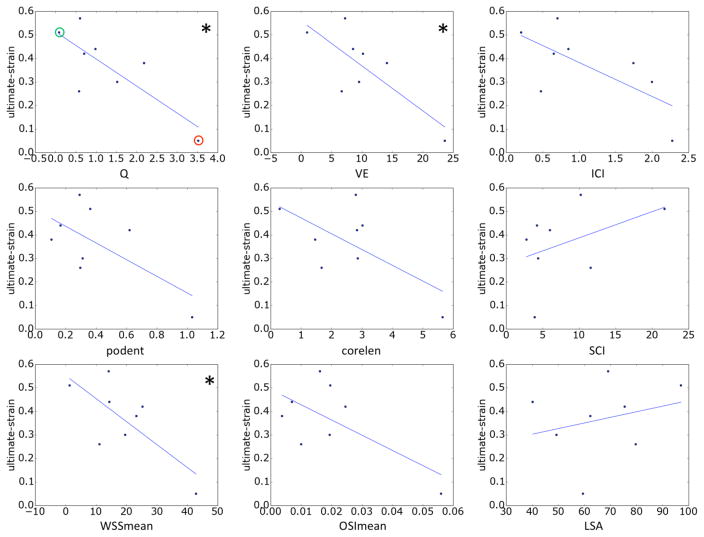
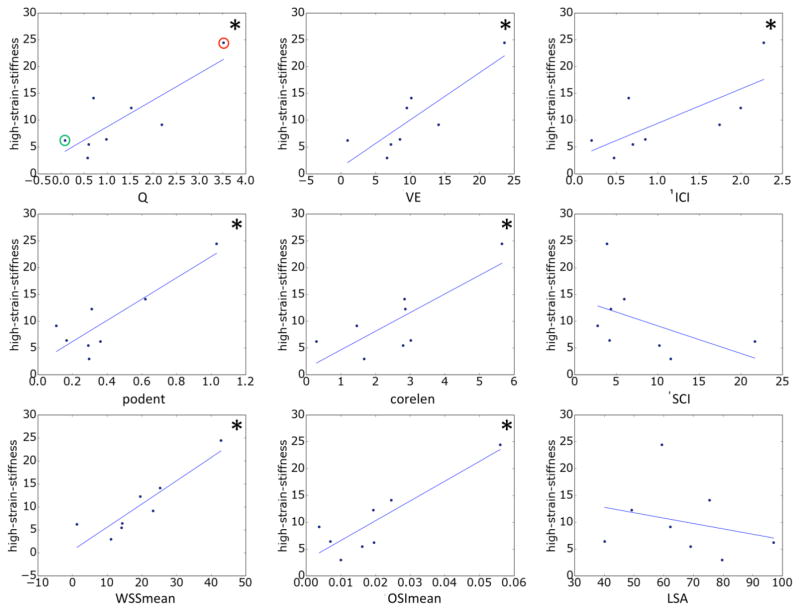
The relationships between hemodynamic quantities and ultimate strain and high-strain wall stiffness are presented in Figure 2 and Figure 3, respectively. The lines correspond to the straight lines fitted by the linear regression (slope and intercept given in Table 3). Correlations that reached statistical significance have been indicated with a ‘*’.

Figure 2.

Relationship between hemodynamic variables and wall ultimate strain. Correlations that reached statistical significance (95% confidence) are marked with a *. In the top-left panel aneurysms CA26 and CA15, exemplified in Figures 4 and 5, are marked with green and red circles, respectively.

Figure 3.

Relationship between hemodynamic variables and wall stiffness at high stress. Correlations that reached statistical significance (95% confidence) are marked with a *. In the top-left panel aneurysms CA26 and CA15, exemplified in Figures 4 and 5, are marked with green and red circles, respectively.

The ultimate strain is seen to decrease with aneurysm inflow rate, mean velocity, inflow concentration, flow instability, flow complexity, WSS and OSI; while it increases with the concentration of the WSS distribution and area under low WSS. However, only the associations with inflow rate, mean velocity, and mean WSS reached statistical significance. Ultimate stress followed the same trends but did not reach statistical significance (data not shown).

The high-stress wall stiffness increases with inflow rate, mean velocity, inflow concentration, flow instability, flow complexity, WSS and OSI; while it decreases with the concentration of the WSS distribution and area under low WSS. The relation to velocity, flow instability, WSS and OSI reached statistical significance.

Two aneurysms (CA26 and CA15), representing distinct mechanical behaviors, are considered in greater detail in Figure 4 to illustrate these trends. In particular, with respect to failure properties, the wall of CA26 (green circle in Figure 2, green curve in Figure 1) had the largest ultimate strain, largest ultimate tension and nearly the largest ultimate stress. The walls of CA15 (red circle, red curve) had the lowest ultimate strain, lowest ultimate tension and the second lowest ultimate stress. With regards to the nature of the loading curve, CA26 had the largest transition strain and nearly the lowest stiffness in the high stress regime. In contrast, the walls of CA15 had the lowest transition strain and the largest stiffness in the high stress regime. Namely, CA26 was stronger with a softer response at high stress than CA15.

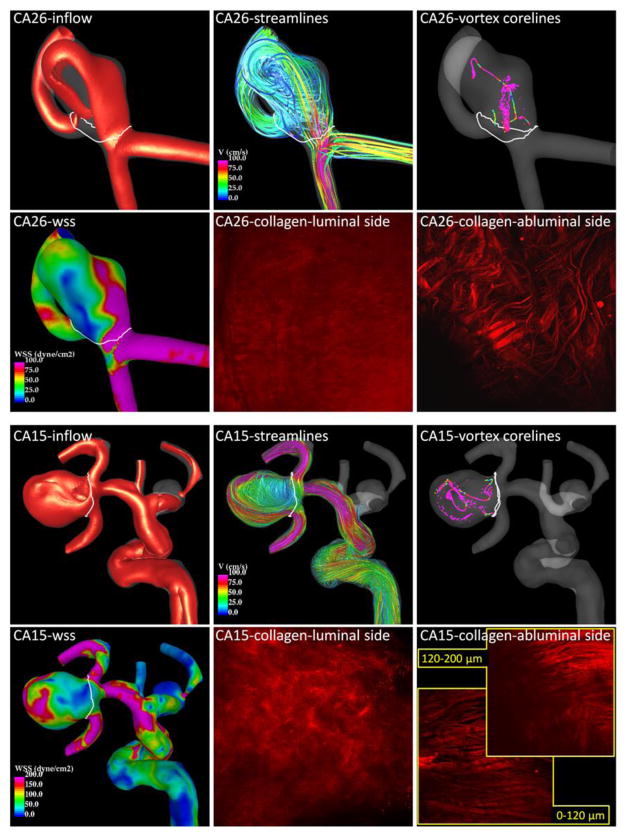
Figure 4.

Flow and collagen fibers in two example aneurysms. Aneurysm CA26 (top panel) corresponds to the green circles of Figures 2 and 3, and the green curve of Figure 1. Aneurysm CA15 (bottom panel) corresponds to the red circles of Figures 2 and 3, and the red curve of Figure 1.

Flow visualizations of CA26 and CA15 along with MPM images of the collagen fibers of each aneurysm in their unloaded configurations are shown in Figure 4. Iso-velocity surfaces (top left frame of each panel) show a stronger inflow stream and larger intra-saccular velocity in CA15. Flow streamlines (top center frame of each panel) also demonstrate stronger intra-saccular flow penetrating deeper into the cavity of CA15. Vortex core-lines (top right frame of each panel) indicate a more complex and unstable flow pattern within CA15. The WSS distribution (bottom left frame of each panel) shows higher values and more irregular WSS distribution in CA15.

The collagen fiber architectures of these two aneurysms are qualitatively different. On the luminal (medial) side, CA26 shows a denser distribution resulting in a smoother and more homogeneous appearance under the MPM than CA15. On the abluminal (adventitial) side, the fibers of CA26 appear to have more than one preferred orientation direction. The fibers seem to form an interlaced mesh pattern and exhibit a larger degree of waviness. In contrast, the fibers of CA15 close to the abluminal surface appear to follow roughly a single orientation without much interlacing, while the fibers deeper in the wall are not unidirectional. Fibers of CA15 exhibit less waviness and are in general thicker. The wall thickness was 450 μm in CA26 versus 130 μm in CA15.

DISCUSSION

Although it is generally accepted that aneurysm evolution is governed by progressive degradation of the wall in response to abnormal hemodynamics [7, 8], the detailed mechanisms that drive the degeneration and weakening of the wall remain unknown [5]. Previous studies have identified possible associations between different hemodynamic factors and aneurysmal rupture [4]. However, it is unclear which parameters are responsible for the mechanisms controlling wall degradation and aneurysm rupture or stabilization [19]. Determining the influence of intra-aneurysmal hemodynamics on wall structure and strength has the potential for resolving this issue.

A prior study found rupture site could best be explained in eight of nine aneurysms through an association of thinner and stiffer walls with regions of abnormally high WSS [20]. Results from the current study seem to support the idea that large flow activity within the aneurysm, as characterized by high velocity and inflow rate, high WSS and OSI, and complex unstable flow structures tend to be associated with lower ultimate strains and stiffer walls. While parallel trends with respect to ultimate stress and ultimate stress did not reach statistical significance, they were in agreement with this trend and warrant further study. In addition, the trends of this study suggest increasing the area exposed to low WSS increases the ultimate strain and decreases the high strain stiffness of the aneurysm wall.

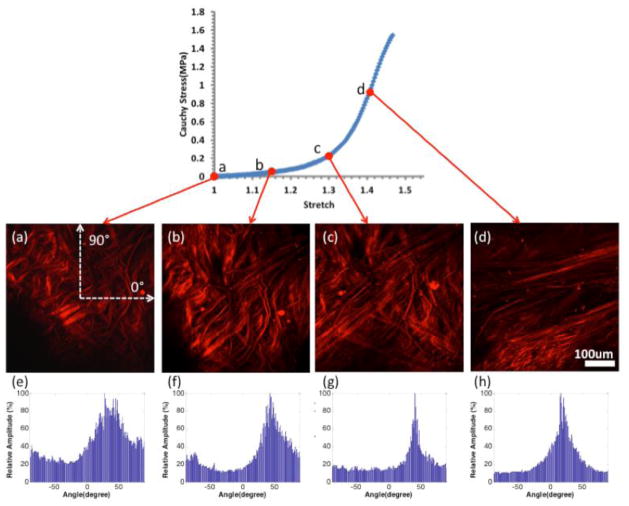
In the low stress region, collagen fiber are found to straighten and reorient as they are recruited to load bearing [12]. This can be seen in Figure 5, which displays MPM images of tissue from CA26 under increasing uniaxial load, and corresponding histograms of the distribution of fiber orientations calculated following [21]. In the toe region, fibers straighten as the tissue is loaded. As loading progresses through the transition regime, increasing numbers of fibers are straightened and recruited to load bearing. Finally, in the high stress regime, small changes in stretch require large increases in load, consistent with the extensive state of recruitment of the collagen fibers. Hence, the high-strain stiffness of the tissue reflects the properties of recruited fibers. Stiffer behavior in the aneurysm wall, would suggest a higher density of collagen fibers or a stiffer collagen fabric, perhaps due to increased cross linking. The larger waviness of collagen fibers in CA26 could explain its increased toe region relative to CA15 that showed little waviness. The magnitude of ultimate strain is influenced by a number of factors including the size of the toe region, high stress stiffness and ultimate stress. CA15 failed at lower strain relative to other samples, consistent with the combined effects of a smaller toe region, greater high strain stiffness and lower ultimate stress. The increased stiffness at high stress in this sample is consistent with a higher density of abluminal collagen fibers. In contrast, CA26 failed at higher strain, which is consistent with its longer toe region, lower high-strain stiffness and greater ultimate stress.

Figure 5.

Abluminal view of collagen fiber recruitment during uniaxial loading of aneurysm sample CA26 (green in Figures 1–3) obtained using the UA-MPM system. The images are obtained at stretches of (a) 1.0 (b) 1.15 (c) 1.3 (d) 1.4 and are formed from a projection of stacks over an approximately 95 μm width of tissue. (e), (f), (g) and (h) are the histograms of fiber orientation distribution of the MPM images at stretch of 1.0, 1.15, 1.3 and 1.4 respectively. 0° is the horizontal direction on the image, and 90° is the vertical direction on the image, as shown in (a).

Our results suggest the hemodynamic environment within the aneurysm sac influences the mechanical behavior of the aneurysm wall that in turn is strongly dependent on the architecture and quality of collagen fibers. The direct connection between hemodynamic conditions and collagen architecture has not yet been explored and is the focus of our ongoing research.

We assessed the connection between global hemodynamic variables and wall mechanical and failure properties. Such global hemodynamic characteristics are appealing because they are less sensitive to local geometric features. While this is a sound approach, in some aneurysms local flow properties may cause focal changes to the wall, which can in principle be the cause of failure. While some of the hemodynamic parameters considered here such as shear concentration index reflect local features, the analysis was not performed locally. In the future, it would be valuable to find ways to directly map local mechanical properties to local hemodynamics to extend the current study.

The current study considers unruptured aneurysms. While the unruptured population appears to harbor aneurysms vulnerable to rupture [12], it would be valuable to explore whether trends identified in this study are seen in ruptured aneurysms. The ruptured population is known to include a subpopulation with thin hypocellular walls devoid of endothelial cells [22]. Hence, this subpopulation may represent a later stage of aneurysm progression where the role of hemodynamics is fundamentally different than for the unruptured population.

The current study suffers from some limitations. The trends reported in this paper need to be confirmed with larger datasets. A number of idealizations are imposed in the hemodynamics studies such as modeling the aneurysm wall as rigid and blood as a single-phase fluid with constant viscosity. Our flow conditions were derived from normal subjects and scaled with the patient-specific inflow vessel sizes, but the effects of co-morbidities such as hypertension were not considered. While our assumptions may be reasonable [23], the effects of other co-morbidities should be investigated in future studies. In addition, we considered uniaxial loading, recognizing that in vivo loading is closer to equi-biaxial. This choice is motivated largely by the desire to test the tissues to failure coupled with the small size of the aneurysm samples. Nevertheless our preliminary results are the first to study the link between hemodynamics and aneurysm wall properties and suggest several provocative hypotheses about the relationship between in vivo hemodynamics, wall structure and wall mechanical properties that need to be tested with larger series of human aneurysm tissue samples.

CONCLUSIONS

In unruptured intracranial aneurysms, wall ultimate strain is negatively correlated with aneurysm inflow rate, mean velocity and mean wall shear stress. Wall stiffness in the high stress region is positively correlated with aneurysm inflow rate, mean velocity, wall shear stress, flow complexity and stability.