Effect of hydrogen bond cooperativity on the behavior of water

Abstract

Four scenarios have been proposed for the low-temperature phase behavior of liquid water, each predicting different thermodynamics. The physical mechanism that leads to each is debated. Moreover, it is still unclear which of the scenarios best describes water, because there is no definitive experimental test. Here we address both open issues within the framework of a microscopic cell model by performing a study combining mean-field calculations and Monte Carlo simulations. We show that a common physical mechanism underlies each of the four scenarios, and that two key physical quantities determine which of the four scenarios describes water: (i) the strength of the directional component of the hydrogen bond and (ii) the strength of the cooperative component of the hydrogen bond. The four scenarios may be mapped in the space of these two quantities. We argue that our conclusions are model independent. Using estimates from experimental data for H-bond properties the model predicts that the low-temperature phase diagram of water exhibits a liquid–liquid critical point at positive pressure.

Water’s phase diagram is rich and complex: more than sixteen crystalline phases (1), and two or more glasses (2 –4) have been reported. The liquid state also displays interesting behavior, such as the density maximum for 1 atm at 4 °C. The volume fluctuations 〈(δV)²〉, entropy fluctuations 〈(δS)²〉, and cross fluctuations between volume and entropy 〈δVδS〉, proportional to the magnitude of isothermal compressibility K _T, isobaric specific heat C _P, and isobaric thermal expansivity α _P, respectively, show anomalous increases in magnitude upon cooling (5). Further, these quantities display an apparent divergence for 1 atm at −45 °C (2), hinting at interesting phase behavior in the supercooled region.

Microscopically, liquid water’s anomalous behavior is understood as resulting from the tendency of neighboring molecules to form hydrogen (H) bonds upon cooling with a decrease of local potential energy, decrease of local entropy, and increase of local volume due to the formation of local open structures of bonded molecules. Different models include these H-bond features, but depending on the assumptions and approximations of each model, different conclusions are obtained for the low-T phase behavior. The relevant region of the bulk-liquid state cannot be probed experimentally, and none of the theories tested because crystallization of bulk water is unavoidable below the homogeneous nucleation temperature T _H (-38 °C at 1 atm).

Four Scenarios for Supercooled Water

Due to the difficulty of obtaining experimental evidence, theoretical and numerical analyses are useful. Four separate scenarios for the pressure–temperature (P–T) phase diagram have been proposed:

(I) The stability limit (SL) scenario (6) hypothesizes that the superheated liquid–gas spinodal at negative pressure reenters the positive P region below T _H(P). In this view, the liquid state is delimited by a single continuous locus P _s(T), bounding the superheated, stretched, and supercooled states. There is no reference to the phase into which the liquid transforms when P → P _s(T). As the spinodal is approached K _T, C _P, and |α _P| → ∞. A thermodynamic consequence of the SL scenario is that the intersection of the retracing spinodal with the liquid–vapor coexistence line must be a critical point (2). The presence of such a critical point in the liquid–vapor transition, although possible, is not confirmed by any experiment. This fact poses a serious challenge to the SL scenario.

(II) The liquid–liquid critical point (LLCP) scenario (7) hypothesizes a first-order phase transition line between two liquids—a low density liquid (LDL) and a high density liquid (HDL)—that terminates at a liquid–liquid critical point C ^′. HDL is a dense liquid with a highly disordered structure, whereas LDL has a lower density and locally tetrahedral order. The experimentally observable high density amorphous and low density amorphous solids correspond in this scenario to a structurally arrested state of HDL and LDL, respectively (8, 9). Starting from C ^′, the locus of maxima of the correlation length ξ (the Widom line) projects into the one-phase region (10). Asymptotically close to the critical point, response functions can be expressed in terms of ξ, hence these too will show maxima, for example, as a function of T upon isobaric cooling. These maxima will diverge upon approaching C ^′. Furthermore, for P > P _C^′, the pressure of C ^′, the response functions will diverge by approaching the spinodal converging to C ^′. Specific models suggest (7, 11) that P _C^′ > 0, but the possibility P _C^′ < 0 has also been proposed (12,13).

(III) The singularity-free (SF) scenario (5, 14) hypothesizes that the low-T anticorrelation between volume and entropy is sufficient to cause the response functions to increase upon cooling and display maxima at non-zero T, without reference to any singular behavior. Specifically, Sastry et al. (14) consider the temperature of maximum density (TMD) line, where the density has a maximum as a function of temperature and prove a general thermodynamic theorem establishing the proportionality between the slope of the TMD (∂P/∂T)_TMD and the temperature derivative of K _T. Thus, because the TMD has negative slope in water, (i. e., (∂P/∂T)_TMD < 0), it follows that K _T must increase upon cooling, whether there exists a singularity or not.

(IV) The critical-point free (CPF) scenario (15) hypothesizes an order–disorder transition, with possibly a weakly first-order transition character, separating two liquid phases and extending to P < 0 down to the superheated limit of stability of liquid water. This scenario effectively predicts a continuous locus of stability limit spanning the superheated, stretched, and supercooled states because the spinodal associated with the first-order transition will intersect the liquid–gas spinodal at negative pressure. No critical point is present in this scenario.

These four scenarios predict fundamentally different behavior, though each has been rationalized as a consequence of the same microscopic interaction: the H-bond. A question that naturally arises is whether the macroscopic thermodynamic descriptions are in fact connected in some way. Previous works have attempted to uncover relations between several of the scenarios, for example between (I) and (II) (11, 16) or (II) and (III) (17, 18). Here we offer a relation linking all four scenarios showing that (a) all four can be included in one general scheme, and (b) the balance between the energies of two components of the H-bond interaction determines which scenario is valid. Morevover, we argue that current estimates of values for these energies support the LLCP scenario.

Cooperative Cell Model of Water

We analyze a microscopic model of water in which the fluid is divided into N cells with nearest neighbor (NN) interactions (19). The division is such that each cell is in contact with four NNs mimicking the first shell of liquid water (20). At the present level of description we therefore, allow for the formation of at most four H-bonds per molecule. The case of a shared H-bond, due to more than four molecules in the first shell, is assimilated with the case in which a H-bond is broken because the interaction energy of a shared bond is less than half the energy of a single H-bond (21, 22). Furthermore, molecules are allowed to form bonds only with NNs, hence structures with interpenetrating H-bonds such as those found in ices VII and VIII are beyond our present scope.

The goal of the model is to represent, microscopically, the essential features of the interaction among water molecules, while being able to qualitatively understand the importance of each of these features. To this end the interaction among cells is separated into four distinct components.

The first component of the interaction is due to the short-range repulsion of the electron clouds. This is incorporated into the model by assigning to each cell i∈[1,N] (a) a volume v _i≥v ₀, where v ₀ is the exclusion volume per molecule, and (b) a maximum of one molecule.

The second component includes all the isotropic long-range attractive interactions such as the instantaneous induced dipole–dipole (London) interactions between the electron clouds of different molecules or the isotropic part of the H-bond (23). We refer to this component as the van der Waals attractive interaction, keeping in mind, however, that this component includes not only the (weak) London dispersion interaction, but also the (stronger) isotropic interaction of the H-bond. The overall sum of the isotropic —attractive and repulsive— interactions can be represented in different ways. The one we adopt in a mean-field (MF) treatment is

[1]

where we set the index n _i = 0 if v ₀/v _i ≤ 0.5, and we set n _i = 1 if 0.5 < v ₀/v _i ≤ 1, hence n _i = 0 if the density in the cell is gas-like, and n _i = 1 if the density in the cell is liquid-like; ϵ > 0 is the characteristic energy of the attraction and the sum is over all NN pairs 〈i,j〉.

The characteristic feature of H₂O is its ability to form H-bonds between neighboring molecules. This interaction has a strong directional component due to the dipole–dipole interaction between the highly concentrated positive charge on each H and each of the two excess negative charges concentrated on the O of another water molecule. Accordingly, the third component incorporated here is an orientational–dependent interaction, that includes the covalent component of the bond (24). To account for the orientational degrees of freedom of each water molecule, we assign to each cell i four bond variables σ _ij = 1, ...,q (one for each NN cell j), representing the orientation of molecule i with respect to molecule j. We choose the parameter q by selecting 30° as the maximum deviation from a linear bond (i.e., q ≡ 180°/30° = 6), hence every molecule has q ⁴ = 6⁴ ≡ 1296 possible orientations. The effect of choosing a different value for q has been analyzed in ref. 25. We say that a bond is formed between cells i and j if σ _ij = σ _ji.

Experiments show that formation of the H bonds leads to an open—locally tetrahedral—structure that induces an increase of volume per molecule (2, 26). This effect is incorporated in the model by considering the total volume to be given as

[2]

where

[3]

is the total number of H-bonds, δ _a,b = 1 if a = b, δ _a,b = 0 if a ≠ b, and v _HB is the volume increase per H-bond (14). Bond formation also leads to a decrease in the local potential energy, hence we add to the Hamiltonian in (Eq. 1) the term

[4]

where J > 0 is the characteristic energy of the covalent (directional) component of the H-bond.

Another key experimental fact is that at low T the O–O–O angle distribution in water becomes sharper around the tetrahedral value (27), suggesting an interaction that induces a cooperative behavior among bonds. For water, four–body and higher order interactions seem to be negligible with respect to the three–body term (28, 29). Hence, the fourth component to the interaction potential is the many–body effect due to H-bonds (30 –32), that minimizes the energy when the H-bonds of nearby molecules assume a tetrahedral orientation. This is accomplished by further adding to the Hamiltonian in Eqs. 1 and 4 the term

[5]

where J _σ > 0 is the characteristic energy of the cooperative component of the H-bond, and (k,ℓ)_i indicates one of the six different pairs of the four bond variables of molecule i. This interaction introduces a cooperative behavior among bonds, which may be fine tuned by changing J _σ. Choosing J _σ = 0 leads to H-bonds that form independently of neighboring bonds (14), whereas J _σ → ∞ leads to fully dependent bonds (33). The total Hamiltonian is now given by

[6]

This model is studied using both MF analysis and Monte Carlo (MC) simulations (25, 34 –37). Details of the MF and MC techniques are available elsewhere (25, 38). In the following we adopt , , and v _HB = v ₀/2.

Mean-Field Results

Four qualitatively different phase diagrams are found dependent on the strengths of the H-bond energy parameters and (Fig. 1).

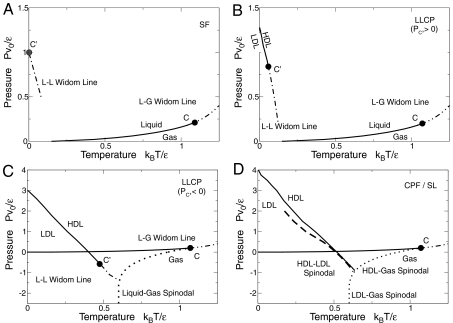
Fig. 1.

Phase diagram predicted from MF calculations for the cell model with fixed H-bond strength (), fixed H-bond volume increase (v _HB/v ₀ = 0.5), and different values of the H-bond cooperativity strength . (A) Singularity-free scenario (). At high T, liquid (L) and gas (G) phases are separated by a first order transition line (thick line) ending at a critical point C, from which a L–G Widom line (double-dot-dashed line) emanates. In the liquid phase, maxima of K _T and |α _P| converge to a locus (dot-dashed line). At C ^′ both K _T and |α _P| have diverging maxima. The locus of the maxima is related to the L–L Widom line for T _C^′ → 0 (see text). (B) LLCP scenario with positive critical pressure (for ). At low T and high P, a HDL and a LDL are separated by a first order transition line (thick line with HDL/LDL labeled) ending in a critical point C ^′, from which the L–L Widom line (dot-dashed line) emanates. Other symbols are as in the previous panel. (C) LLCP scenario with negative critical pressure (for ). Here the L–L Widom line (dot-dashed line) is shown intersecting the L–G spinodal (dotted line). Other symbols are as in the previous panel. (D) Critical-point free scenario (). The HDL–LDL coexistence line extends to the superheated liquid region at P < 0, reaching with the liquid spinodal (dotted line). The stability limit (SL) of water at ambient conditions (HDL) is delimited by the superheated L–G spinodal and the supercooled HDL–LDL spinodal (dashed line), giving a reentrant behavior as hypothesized in the SL scenario. Other symbols are as in the previous panels. In all panels, k _B is the Boltzmann constant.

When the model coincides with that proposed in ref. 14, which gives rise to the SF scenario (Fig. 1 A). For the model displays a liquid–liquid transition ending in a LLCP at P _C^′≥0 (Fig. 1 B) (34). For , where a = 0.30 ± 001 and b = 0.36 ± 0.01 are fitting parameters, a LLCP occurs at P _C^′ < 0 (Fig. 1 C). For , a liquid–liquid transition with no critical point is found, consistent with the CPF scenario (Fig. 1 D). In Fig. 2 we summarize these results in the vs. parameter space.

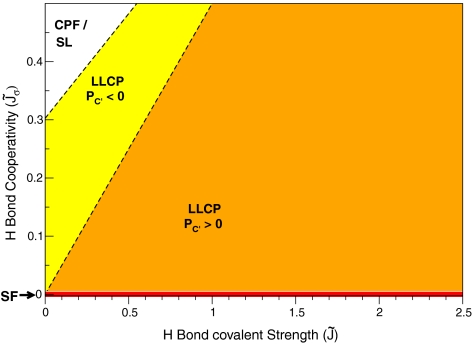
Fig. 2.

Possible scenarios for water for different values of H-bond energies (covalent or directional component) and (cooperative or three-body component), both in units of the van der Waals energy ϵ, were obtained from MF calculations. The ratio v _HB/v ₀ is kept constant. (i) If (red line along x-axis), the SF scenario is realized independent of . (ii) For large enough , water would possess a first-order L–L phase transition line terminating at the L–G spinodal—the CPF scenario; the liquid spinodal would retrace at negative pressure, as in the SL scenario (white region in top left). (iii) For other combinations of and , water would be described by the LLCP scenario. For larger , the LLCP is at negative pressure (yellow region between dashed lines). For smaller , the LLCP is at positive pressure (orange region in bottom right). Dashed lines separating the three different regions correspond to MF results of the microscopic cell model. Equations for the lines are and , with a ≃ 0.3 and b ≃ 0.36. The P - T phase diagram evolves continuously as and change.

Limiting Behavior Between the Four Cases.

In the following we discuss how, by tuning and , we can pass from one scenario to another in a continuous way.

(i) By beginning with the LLCP scenario and studying the limit , we find T _C^′ → 0. Moreover, we find that K _T and |α _P| diverge as |T - T _C^′|^-1 for any value of J _σ including J _σ → 0 and T _C^′ → 0. Furthermore, we find for the entropy S that for any value of J _σ and T _C^′≥0, (∂S/∂T)_P ∝ |T - T _C^′|^-1. Hence, C _P ≡ T(∂S/∂T)_P diverges as |T - T _C^′|^-1 when T _C^′ > 0 while C _P is constant as in the SF scenario (39) when T _C^′ = 0 (). Therefore, the SF scenario coincides with the LLCP scenario in the limiting case of T _C^′ → 0 for (Fig. 1 A).

(ii) Again, beginning with the LLCP scenario and increasing while keeping other parameters constant, we observe that C ^′ moves to larger T and lower P (Fig 1 B). For is P _C^′ < 0 (Fig. 1 C).

(iii) With further increase of , C ^′ approaches and eventually reaches the liquid–gas spinodal. For larger values of only the liquid–liquid transition remains, which is precisely the CPF scenario (15) (Fig. 1 D). Hence, the CPF scenario differs from the LLCP scenario only in that C ^′ is now inaccessible lying beyond the region of liquid states. The same result may be obtained by decreasing while fixing and other parameters. Here a decrease of moves C ^′ to lower pressure, that is, toward the liquid spinodal, while the entire liquid–liquid phenomena moves to successively lower temperature. In all cases the location of C ^′ varies continuously with variation of and .

(iv) In the case of the CPF scenario we find that the superheated liquid–gas spinodal merges with the supercooled liquid–liquid spinodal, as in ref. 11. This gives rise to a liquid spinodal that retraces in the P–T plane. This feature resembles the main characteristic of the SL scenario, where the high-T liquid has a limit of stability at P < 0 that retraces toward P > 0 at low T. Here this retracing locus is formed by two spinodal lines, with different signs of the slope that merge at P < 0. Therefore, in the framework of the present model, the CPF scenario and the SL scenario coincide, corresponding to the case in which the cooperative behavior is very strong.

Linearity of the Lines Separating one Scenario from Another in – Plane.

For the cell model we can derive

[7]

and

[8]

Here α > 0 and β < 0 are constants and in the MF context . Symbols , where X is or T _C^′, represent terms of order X ² or higher that are negligible when X ≪ 1. Our MF results confirm the relations in Eqs. 7 and 8 with α ≃ 0.74k _B/ϵ and β ≃ -7.4k _B/v ₀, with negligible terms.

Therefore, we can rewrite the above relations as , when v _HB = v ₀/2. As a consequence, for the case P _C^′ = 0, we find , which is exactly what we find numerically in Fig. 2 along the line separating the LLCP scenario with P _C^′ > 0 (valid for ) and the LLCP scenario with P _C^′ < 0 (valid for ).

It is possible to show that Eq. 8 can be generalized to , where T _LL and P _LL are the T and P along the liquid–liquid transition line. Our MF results are in good agreement with this prediction.

We can estimate the equation of the line separating the LLCP scenario with P _C^′ < 0 and the CPF/SL scenario in the – plane, by using the Eq. 8 together with the equation for the liquid–gas spinodal. In particular, we adopt a parametric fit, in terms of the parameter of the spinodal pressure with respect to the spinodal temperature, and we evaluate the line separating the LLCP and CPF/SL scenarios for when C ^′ is on the spinodal. From this approximate approach, we derive that with of the same order of magnitude of the fitting parameter a ≃ 0.30 in Fig. 2. Yet, γ ≠ 0.36, the value of b in Fig. 2, as a consequence of the strong approximations made.

MC Results

To test the validity of our MF calculations, we perform MC simulations in the NPT ensemble (38). To this end,

(i) we consider that the total volume is V ≡ V _MC + N _HB v _HB, where V _MC⩾Nv ₀ is a dynamical continuous variable;

(ii) we assume that the system is homogeneous with all the variables n _i set to 1; with this assumption the gas state occurs when ρ ≡ N/V < 0.5/v ₀;

(iii) we replace the isotropic repulsive and attractive terms of the Hamiltonian in (Eq. 6) with a Lennard–Jones potential, more suitable for continuous distances r between particles, with attractive energy ϵ > 0 plus a hard-core repulsion at distance r ₀:

[9]

Here r ₀ ≡ (v ₀)^1/d and d is the system dimension (34) (the hard-core repulsion reduces the computational cost and does not change the phase diagram). To avoid the interaction of a molecule with any other molecule, as it would be in MF, in the U _W(r) calculation we do not consider the volume changes due to the H-bonds formation. Therefore, the distance between two NN molecules is (V _MC/N)^1/d, and the distance r between two generic molecules is the Cartesian distance between the centers of the cells in which they are enclosed.

(iv) We consider the system in d = 2 dimensions. Whereas the MF results are valid for any dimension so long as the number of NN molecules is 4, the MC results hold for a system with coordination number 4 and 2 dimensions. Since the results in the two cases are qualitatively comparable, we do not expect a strong dependence of the phase diagram on dimension.

We simulate this system for N = 10⁴ molecules arranged on a square lattice, adopting Wolff’s algorithm to equilibrate at low T (38), for different values of , keeping constant , and v _HB/v ₀ = 0.5 (Fig. 3).

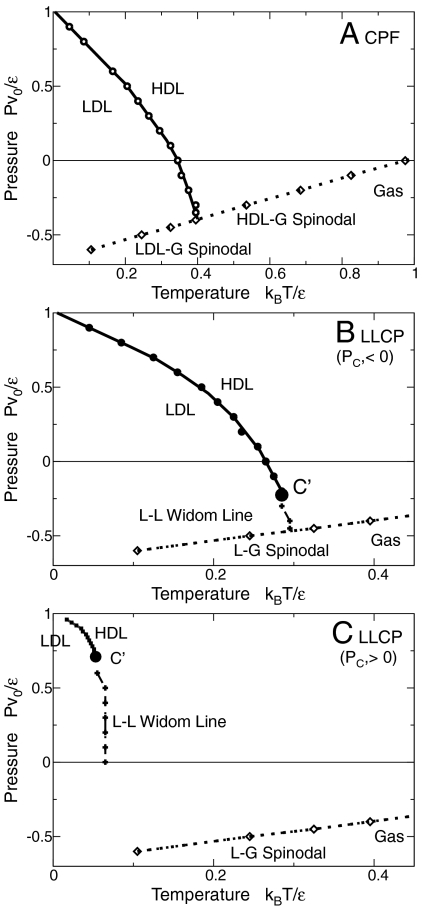
Fig. 3.

Phase diagrams from MC simulations. We fix the parameters , v _HB/v ₀ = 0.5 and vary the parameter . (A) For (i.e., where a and b are given in the text and both are approximately 1/3), we find a L–L phase transition (thick line with circles) ending on the superheated L–G spinodal (dotted line with diamonds) as in the CPF scenario. (B) For (i.e., ), the L–L phase transition ends in a LLCP at negative pressure. (C) For (i.e., ), the LLCP ends at positive pressure and the line of specific heat maxima (crosses), emanating from the LLCP and approximating the L–L Widom line, is shown only for positive pressure. In all the phase diagrams, P and T are expressed in internal units and can be converted to real units through the choice of physical values for the parameters ϵ and v ₀ and shifting the resulting phase diagram in accord with an experimental reference point. Errors are of the order of the symbol sizes. Lines are guides for the eyes. Other model parameters are as for MF calculations (see text).

For large values of (), we find a HDL–LDL first-order phase transition that merges with the superheated liquid spinodal as in the CPF scenario (Fig. 3 A). At lower (), a HDL–LDL critical point appears at P < 0, from which emanates the locus of C _P maxima (used here as an approximation of the liquid–liquid Widom line), which intersects the superheated liquid spinodal (Fig. 3 B). By further decreasing (), the HDL–LDL critical point occurs at P > 0, with the line of C _P maxima intersecting the P = 0 axis (Fig. 3 C). For , approaching zero, we find that the temperature of the HDL–LDL critical point approaches zero and the critical pressure increases toward the value P = ϵ/v ₀ independent of . In this case, we can show that Eq. 8 still holds, but with . The line of C _P maxima approaches the T = 0 axis for . These results confirm the qualitative behavior found with the MF calculations.

Comparison with Other Thermodynamic Models

To show that our analysis offers a general framework within which to analyze the supercooled water phase diagram in terms of the interplay between the strengths of the directional contribution to the H-bond interaction and its cooperative part, we compare our results with those from other thermodynamic models that can reproduce more than one scenario by tuning appropriate parameters (11, 16, 18).

One free energy model with cooperative interactions is the one introduced by Tanaka (18). He shows that, as in the SF scenario, water’s anomalies are the effect of the excitation of locally favored structures upon cooling, which have lower energy and larger volume than normal liquid structures. As in our model, in Tanaka’s model increasing the cooperativity among excitations of locally favored structures leads to the LLCP scenario. Moreover, Tanaka’s model LLCP is regulated by relations such as our Eqs. 7 and 8. Therefore, by increasing the strength of the cooperative interaction, the LLCP will eventually reach the limit of stability of the liquid as in the CPF/SL scenario.

We next consider the free energy model introduced by Poole et al. (11), in which a van der Waals free energy is augmented to include the effect of H-bond formation. The H-bond interaction is characterized by two free parameters: the strength of the H-bond and a geometrical constraint on H-bond formation. The fraction of molecules that form H-bonds with decreased energy and entropy is determined by a distribution over molar volumes, the width of which is Δ. Poole et al. show that, by keeping Δ fixed, their model displays a SL scenario for weak H-bond energy and a LLCP at positive pressure for strong H-bond energy. This corresponds in our model to increasing the H-bond coupling from to , while keeping fixed.

Next we study the effect of varying the other H-bond parameter in the Poole et al. model, the width Δ. Keeping the H-bond energy fixed, we produce the LLCP phase behavior at large Δ and the SL phase behavior at small Δ. Hence a decrease of Δ has the same effect on the phase diagram as an increase in the H-bond cooperativity in our model.

This result is consistent with that of Borick et al. (16) for their Hamiltonian model that incorporates the cooperativity of H-bonds through the same mechanism used by Poole et al., that is, by adopting a distribution with width Δ that makes the H-bond strength density dependent. By decreasing Δ, Borick et al. find that the LLCP moves to lower P and higher T. This behavior makes sense physically, as a more all-or-nothing distribution of H-bonds (small Δ) implies a more cooperative process of bond formation. It also implies that the models of Poole et al. and Borick et al. give rise to the SF scenario only in the limiting case of infinite Δ.

We conclude that all four models give a consistent physical picture. This suggests that our result, expressed in terms of strength of the directional and cooperative components of the H-bond, as summarized in Fig. 2, is general.

Estimates from Experimental Data

In the framework of the scheme presented here, in which directionality and cooperativity are the two relevant physical parameters, we propose that the way to understand which scenario best describes water is to probe the energy of the covalent part of the H-bond interaction (24) and the energy of the cooperative component of the H-bond interaction (30 –32). Experiments measure H-bonds in ice Ih to be approximately 3 kJ/mol stronger than in liquid water (40). Attributing this increase to a cooperative interaction among H bonds (41) we can estimate the value of J _σ in the cell model to be ≈1.0 kJ/mol. An estimate of the van der Waals attraction based on isoelectronic molecules at optimal separation, yields ϵ ≈ 5.5 kJ/mol (42). The optimal H-bond energy, E _HB, has been measured to be ≈23.3 kJ/mol (43). By considering tetrahedral clusters of H-bonded molecules, with H-bond and van der Waals interactions between NN molecules (and appropriately reduced van der Waals interactions between second and third NN molecules), we derive the value for the directional component of the H-bond, J ≈ 12.0 kJ/mol. Other experimental estimates suggest that breaking the directional component of the H-bond requires ≈6.3 kJ/mol (44).

Both estimates from experiments fall within the range of , with , that is, with . Therefore, within our model, these values lead to the LLCP scenario with P _C^′ > 0.

Conclusions

We have shown that a microscopic cell model of water, by taking into account the cooperativity among H-bonds, is able to produce phase behaviors consistent with any of the proposed scenarios for water’s phase diagram. It is the amount of cooperativity in relation to the strength of the directional component of the H-bond that establishes which scenario holds. For no amount of cooperativity, the SF scenario is recovered. By increasing the amount of cooperativity in relation to the H-bond directional strength, a liquid–liquid transition grows out from the T = 0 axis, ending in a LLCP. With sufficiently strong cooperativity, this LLCP lies beyond the region of stable liquid states, leaving only the liquid–liquid transition, consistent with the CPF scenario. In this case the spinodal associated with the transition acts as the line predicted in the SL scenario.

Comparison with previous models gives consistent results. Hence we argue that each of the four scenarios proposed for the phase diagram of liquid water may be viewed as a special case of our general scheme. This scheme is based on the assumption that water–water interaction is characterized by an isotropic component, a directional component, and a cooperative component and that H-bond formation leads to an open local structure. Alternative mechanisms, based only on isotropic interactions (45 –49) or only on directional interactions (50) have been considered and their relevance for the water case is an open question. Finally, estimates for the three components of the H-bond interaction, based on experimental data lead to the conclusion that the LLCP scenario with a positive critical pressure holds for water.