Brain Metabolites B₁–Corrected Proton T₁ Mapping in the Rhesus Macaque at 3 T

Abstract

The accuracy of metabolic quantification in MR spectroscopy (MRS) is limited by the unknown radio-frequency field (B₁) and longitudinal relaxation time (T₁). To address both issues in proton (¹H) MRS we obtained B₁-corrected T₁ maps of N-acetylaspartate (NAA), choline (Cho) and creatine (Cr) in five healthy rhesus macaques at 3 T. For efficient use of the 4 hour experiment, we used a new three-point protocol that optimizes the precision of T₁ in 3D ¹H-MRS localization for extensive, ~30%, brain coverage at (0.6×0.6×0.5 cm)³=180 μL spatial resolution. The resulting mean±standard error (SEM) T₁s in 700 voxels were: NAA=1232±44, Cr=1238±23 and Cho=1107±56 ms. Their histograms from all 140 voxels in each animal were similar in position and shape - characterized by SEMs of the full width at half maximum divided by their means, of better than 8%. Regional gray matter NAA, Cho and Cr T₁s: 1333±43, 1265±52 and 1131±28 ms were 5–10% longer than white matter: 1188±34, 1201±24 and 1082±50 ms (statistically significant for the NAA only), all within 10% of the corresponding published values in the human brain.

Introduction

The similarities between the rhesus macaque brain and its human counterpart have lead to use of the former in studies of neurological disorders and their treatment (1–4). Due to the serial nature and high cost of these studies, non-invasive modalities: MRI for morphology or function and proton MR spectroscopy (¹H-MRS) for metabolism, are often favored. The latter can be used to monitor neuronal cells, cell energetics and membrane turnover by quantification of their surrogate metabolic markers (5,6): N-acetylaspartate (NAA), creatine (Cr) and choline (Cho).

Metabolic quantification requires knowledge of several parameters that influence the ¹H-MRS signal. Some, e.g., the echo- and recycle times (TE, TR) or voxel size are known. Instrumental factors such as the static (B₀) and radio-frequency (RF, B₁) field inhomogeneity can be handled by field mapping and internal water referencing (7–9). Accounting for the molecular environment, however, requires knowledge of the local transverse (T₂) and longitudinal (T₁) relaxation times (5). Although T₁- and T₂-weighting can be minimized at TE «T₂ and TR»T₁, the latter reduces both coverage and the signal-to-noise-ratio (SNR), thereby limiting the spatial resolution (10,11). Given the small, ~80 cm³, average macaque brain(12), either limitations can become prohibitive.

To optimize SNR/unit-time for the net α=90° nutation, ¹H-MRS is often done at TR≈1.2·T₁ (11), that also subjects the metabolites’ signals to unknown T₁-weighting. Furthermore, the RF field itself can suffer regional variations that worsen with increasing B₀ (13,14). Consequently, the observed steady-state MR signal, S, exhibits a complex dependence on B₁ and T₁ (15):

$$S={\rho }_0\frac{1-exp(-TR/T_1)}{1-exp(-TR/T_1)cos(B_1\alpha )}sin(B_1\alpha ),$$ [1]

where α is the target nutation and B₁, the ratio between the actual local and nominal B₁ value, can exceed 20% at 4 T and 40% at 7 T over regions the size of a human head (13). Unknown B₁ and T₁ combine to confound determining ρ₀, the voxel spin density, i.e., metabolic quantification.

In this paper we mapped the B₁-corrected T₁s of NAA, Cr and Cho at 3 T over ~30% of the macaque brain with three dimensional (3D) ¹H-MRS at 180 μL spatial resolution in a three-point protocol that optimizes their precision per unit time (15). This also enabled us to test two implicit hypotheses often made in ¹H-MRS (5,16): First, that inter-animal metabolite T₁ distributions are sufficiently similar that obtaining them once is enough. Second, that regional T₁s are similar enough that one value per metabolite suffices for reliable quantification using Eq. [1].

Materials and Methods

Non Human Primates

One male and four female healthy adult (3 – 5 years old, 3.9 – 6 kg) rhesus macaques (Macaca mulatta) were studied. Each was tranquilized with 15 – 20 mg/kg intra-muscular ketamine hydrochloride and intubated to ensure a patent airway during the experiment (no mechanical ventilation was needed). Intravenous injection of 0.4 mg/kg atropine was administered to prevent bradycardia and continuous infusion of 0.25 mg/kg/min propofol was maintained throughout via catheter in a saphenous vein. Heart and respiratory rates, oxygen saturation and end-tidal CO₂ were monitored continuously and a water blanket used to prevent hypothermia. The animals were under constant veterinary supervision and the protocol was approved by the Harvard Medical School and Massachusetts General Hospital IACUCs.

MRI and ¹H-MRS

All experiments were done in a 3 T whole-body MR imager (Magnetom TIM Trio, Siemens AG, Erlangen, Germany) with a circularly-polarized transmit-receive human knee coil. To guide the ¹H-MRS volume of interest (VOI) we acquired sagittal, coronal and axial turbo spin echo MRI at TE/TR=15/10000 ms, 512×512 matrix, 140×140 mm² field of view (FOV) and 1 mm slice thickness. A 4.2×3.0×2.0 cm³ anterior-posterior × left-right × inferior-superior (AP×LR×IS) VOI was then image-guided along the splenium-genu axis of the corpus callosum, as shown in Fig. 1a and b. The manufacturer’s automatic shim procedure then adjusted its water linewidth to a consistent 26±1 Hz full-width-at-half-maximum (FWHM).

Fig. 1.

Top: Sagittal (a) and axial (b) T₂-weighted MRI from a macaque head showing VOI and FOV (solid and dashed white frames) placement and their relative size.

Bottom: Real part of the axial 5×7 (LR×AP) spectra matrices from the VOI on slice b for each of the TR_i, averages-N_i and flip-angles, α_i (i=1..3), on common 3.6 – 1.6 ppm and intensity scales. Note the spectral resolution and SNRs at each of the three TRs.

The VOI was selectively excited using TE=42 ms PRESS with the first 5.12 ms RF pulse also performing 4^th-order transverse Hadamard encoding in the IS direction (17,18). Its 4.5 mT/m slice-select gradient applied kept the chemical shift displacement between NAA and Cho under 0.08 cm, ~16% of the slices thickness (18). The AP and LR aspects of the VOI were defined by numerically optimized 15.4 ms 180°s pulsed under 1.9 and 2.7 mT/m, sustaining 0.18 and 0.13 cm (30% and 22%) relative displacement between NAA and Cho at the VOI edges. The slices’ LR×AP planes were partitioned with 16×16 chemical shift imaging (CSI) over a 9.6×9.6 cm² FOV into 0.6×0.6 ×0.5 cm³ (180 μL) voxels. With no k-space filters applied the effective resolution, accounting for full width at half maximum of the point spread function for the uniform 2D phase encoding, was 226 μL (19). [In the Hadamard direction the nominal equals the actual voxel size (20)]. The signal was acquired for 256 ms at ±1 kHz bandwidth.

Choice of acquisition parameters

Since T₁ precision is a function of the source data SNR (15,21), noisy ¹H-MRS experiments at high spatial resolution lead to long acquisition. For its efficient use we combined two approaches: (i) TriTone - a three-point scheme optimizing B₁ and T₁ precision by manipulating the number of averages: N₁, N₂, N₃ and nominal flip angles: α₁, α₂, α₃, at TR₁, TR₂ and TR₃ (15). (ii) 3D ¹H-MRS to cover extensive brain volume at the same SNR as single-voxel methods (11,22).

Since the uncertainty in TriTone-estimated T₁s varies by less than 10% from ×0.8 to ×1.6 of the T₁^tune for which the protocol is adjusted, we used 800 ms for that parameter to keep the total experiment duration to under 4 hours. This led to the following three-point protocol (15): TR₁=600 ms, α₁=85°, N₁=8 (for 82 min.); TR₂=1280 ms; α₂=40°, N₂=1 (22 min.); and TR₃=3600 ms, α₃=115°, N₃=2 (123 minutes). To keep the SAR within the FDA approved limits in human subjects for the shortest TR=600 ms acquisition we extended each of the two PRESS 180° pulses to 15.4 ms leading to a TE of 42 ms.

Post-processing and T₁ determination

The ¹H-MRS data were processed off-line with in-house software. Residual water signals were removed in the time domain (23), voxel-shift aligned the CSI grid with the NAA VOI and the data was zero-filled to 2048 and 32×32 in the time and axial (CSI) directions. [Although it does not add new information to the raw data, Zero-filling can increase the effective spatial resolution by providing overlapping voxels that can reduce partial volume effects (24,25)]. Fourier and Hadamard transforms in the time and spatial dimensions followed with frequency and zero-order phase shifts done automatically in reference to the NAA peak in each voxel.

Relative level of the i-th metabolite (i=NAA, Cr or Cho) at each point, S_1i, S_2i, and S_3i, were estimated from their peak area with the Spectroscopic Imaging Toolkit – Fitting (SITools-FITT) parametric spectral modeling and least-squares optimization package of Soher et al. (8) with NAA, Cho, Cr, glutamate, glutamine, taurine and myo-inositol included in the model. The relative level were converted into spherical angles:

$$\begin{array}{l}\phi =arctan(S_{3i},S_{1i})\\ \theta =arcos(S_2/{[{S_{1i}}^2+{S_{2i}}^2+{S_{3i}}^2]}^{1/2}),\end{array}$$ [2]

and polled against a look-up table T₁(φ, θ) constructed based on the sequence parameters (15). Their inter-animal reproducibility was assessed for each metabolite in terms of the coefficient of variation (CV=standard deviation/mean) using as data for each animal the mean over all voxels.

Statistical Analyses

Two-way analysis of variance based on ranks was used to compare brain regions with respect to the mean of each metabolite. Specifically, the data for a given metabolite were first converted to ranks which were then used as the dependent variable in order to satisfy underlying distribution assumptions. The model included animal ID as a random classification factor to allow comparisons to be made within each animal and to account for the lack of statistical independence among observations made for the same animal. Statistical significance was defined as a two-sided p≤0.05. SAS version 9.0 (SAS Institute, Cary, NC) was used for all analyses.

Results

Spectra from one slice at each of the three TriTone acquisition points, shown in Fig. 1, demonstrate the SNRs and spectral resolution. Specifically, metabolite linewidth in each voxel, also estimated by the modeling software, averaged 8.7±3.1 Hz FWHM corresponding to T₂^*s (=1/πΔω assuming Lorentzian shape) of 37±13 ms. The SNRs from the 700 voxels and the inter-animal coefficient of variation in the five macaques, are compiled in Table 1.

Table 1.

The SNR of 700 (35 voxels per slice × 4 slices per animal × 5 animals) voxels (mean±standard deviation) of NAA, Cr and Cho at the three different TRs, and the inter-animal T₁ coefficient of variation (CV) for each of the three metabolites.

Metabolite	SNR			Inter-animal T1 CV
	TR1	TR2	TR3
NAA	31.7±10.1	21.7±7.0	26.4±8.8	3.5%
Cr	22.7±9.3	14.9±5.6	23.7±8.9	1.9%
Cho	14.1±6.8	13.8±6.8	20.9±9.7	4.4%

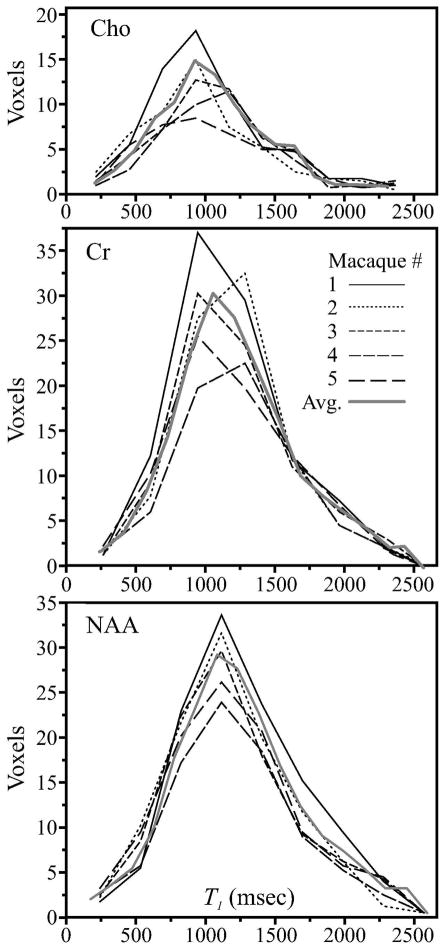
The B₁-corrected T₁ histograms for each metabolite in the 140 voxels from every monkey together with a normalized histogram for each metabolite from the 700 voxels in all the animals, are shown in Fig. 2. Their distributions exhibit a gratifying similarity in: (a) peak position, also reflected by less than 5% inter-animal CV (see Table 1); and (b) width, characterize by the CV of histograms FWHM: NAA=11%, Cr=16% and Cho=19%. The mean ± standard error (SEM) of the 140 T₁s in each of the 5 animals were: NAA=1232±44, Cr=1238±23 and Cho=1107±56 ms. Note that all T₁ values in Table 2 are in the ×0.8 to ×1.6 range about the 800 ms T₁^tune for which the protocol is adjusted, i.e., within 10% of the optimal value obtainable for the acquisition time.

Fig. 2.

Cho, Cr and NAA B₁-corrected T₁s histograms from all 140 voxels in the VOI of each macaque (black lines), as well a normalized histogram for each metabolite formed from the 700 voxels in all the animals (thick solid gray line). Note the inter-animal histogram similarity reflected by the peak position and FWHM for each metabolite and proximity to the “global” histogram from all, suggesting that these distributions are characteristic.

Table 2.

Mean±SEM values of proton T₁ relaxation times (milliseconds) at 3 T of the NAA, Cr and Cho in the various GM and WM brain regions and structures of the rhesus macaque brain shown in Fig. 3.

		T1 (ms)
		NAA	Cr	Cho
GM	Caudate head	1376±61	1370±75	1072±121
	Thalamus	1330±78	1272±30	1099±106
	Lentiform nucleus	1212±70	1293±40	1198±42
	Cingulate gyrus	1413±89	1123±99	1154±75
	aMean±SEM	1335±25	1263±22	1147±68
WM	Splenium of the b CC	1222±33	1176±55	1132±27
	Centrum semiovale	1154±51	1224±49	1032±76
	aMean±SEM	1166±19	1214±41	1047±44

^aMean±SEM of the average of the T₁s in all the structures in that tissue type (GM or WM) in each of the 5 animals.

^bCC – corpus callosum.

Regional T₁s were estimated in the six gray and white matter (GM, WM) brain regions shown in Fig. 3 with their average spectra at each TR overlaid with the SITools-FITT model functions. Each was outlined on the axial MRI and our software averaged the T₁s in all voxels that fell entirely or partially within. No chemical shift displacement (at the VOI edges) or CSF partial volume correction were made since they cancel in the ratios of Eq. [2] and exert only minor influence on T₁ precision in affected voxels (due to lower SNR) but not on its accuracy. The regional values compiled in Table 2 show GM T₁s to be 5 - 10% longer than WM, although this difference was statistically significant only for the NAA.

Fig. 3.

Top: Axial MRI showing the 3×4.2 cm² VOI (thick white frame), CSI grid (thin white lines) and the brain regions where the voxels’ T₁ were averaged (thick white lines): a- cingulate gyrus, d- caudate head, e- lentiform nucleus, f- thalamus in the GM; and b- centrum semiovale and c- splenium of the corpus callosum in WM.

Bottom: Real part of the average spectra from each region and time point (black lines) overlaid with the model lineshapes (gray lines). All are on common 3.7 – 1.6 ppm and intensity scales. Note their improved SNRs versus single-voxel spectra in Fig. 1.

Discussion

Nutation angle variation due to B₁ inhomogeneity (even in volume coils at low fields) is well known to be the main source of T₁ estimation errors (26,27), that worsen at higher B₀s (10,13,14). Unknown B₁ and T₁ combine to impede use of Eq. [1] in two ways. First, the assumption that the nutation equals its nominal value fails due to B₁ variations of 20% and 40% at 4 and 7 T over VOIs the size of a human head (13,26) that can lead to 40% – 80% error in T₁ (26). Second, if TR≈T₁ is used for optimum SNR [even if B₁ variations are addressed through usage adiabatic pulses (28–30)], the lack of knowledge of metabolite T₁’s lowers quantification accuracy.

Although other B₁ mapping methods are available, besides different RF power, imaging time, and post-processing that they require, they all need at a minimum two separate scans each done with different sequence parameters (typically different flip angles) in order to obtain B₁ (26,31). At least two more scans with different acquisition parameters (typically different TRs) are subsequently needed to obtain T₁ (32), rendering the portion of the time used to map B₁ unavailable to measure T₁ and vice versa. TriTone in comparison avails all the time for both. Since the precision of T₁ and B₁ is a function of the SNR of the data (15), this gives TriTone an advantage that increases at higher spatial resolutions that require longer acquisition.

Combining the coverage of 3D ¹H-MRS with the efficiency of TriTone, therefore, enabled us to map the B₁-corrected T₁s of the three main metabolites over 25.2 cm³ (≈30%) of the ~80 cm³ macaque brain at 180 μL spatial resolution and best precision for the 4 hour experiment (15,33). This in turn yielded global and regional T₁s in 5 animals in order to ascertain how characteristic they are (i) across rhesus macaques; and (ii) among different brain regions and tissue types.

Indeed, the inter-animal T₁s distribution reproducibility reflected by the similar metabolite T₁ histograms’ peak-position and shapes (under 10% SEM of their widths - see Fig. 2) support the first hypothesis: that these T₁ distributions are characteristic of the healthy rhesus macaque brain. Consequently, additional measurements even if they were feasible given the time and cost, are unnecessary since they are unlikely to yield significantly different results.

Furthermore, the less than 5% T₁ SEMs for the GM and WM for all metabolites (see Table 2) reflect inter-animal similarity that substantiates the second hypothesis: that for quantification purposes a global mean T₁ for each metabolite is sufficient. Specifically, the GM 5 - 10% longer T₁s will lead to minimal (under 5%) difference in relative T₁-weighting compared with the WM at TR=1.2·T₁≈1450 ms in these regions and metabolites (11). The practical implication is that around this TR use of the mean T₁ for each metabolite suffices to reduce that metabolite’s T₁-weighting quantification errors to below typical voxel noise levels, rendering them insignificant.

The metabolites’ T₁s obtained are all within 10% of the 1.4, 1.2 and 1.3 s reported for NAA, Cr and Cho in the human brain at 3 T (34,35). The minor discrepancies may be due to relatively low, 8–12 cm³, spatial resolution single-voxels without B₁ correction [long recognized as the main source of T₁ estimation errors (27)] of the latter. These may have combined to confound tissue-specific T₁ estimates due to partial WM volume in GM voxels and vice versa, an issue both studies acknowledge but only estimated its impact. Our use of 3D localization allowed us to reduce the voxel-volume nearly 50 fold and to benefit from zero-filling and regional averaging to better resolve GM from WM T₁s by greatly reducing (although not entirely eliminating) partial volume. The similar T₁s together with the validation of the two hypotheses ( vide supra) establish the rhesus macaque brain as a good model for its human counterpart with respect to this molecular environment parameter and also yield two additional encouraging ramifications for ¹H-MRS in this model system. First, only one set of T₁s need be retained for quantification in humans and macaques using Eq. [1]. Second (alternatively), at common TR all the metabolites will incur the same T₁-weighting in the macaque as in the human brain.

Averaging adjacent voxels in the same structure reduces their the CV of the T₁s (from the ~38%, 33% and 40% for NAA, Cr and Cho, estimated from the half-width at half height of the histograms in Fig. 2) via two mechanisms: Primarily due to smaller T₁ variations in similar tissue that lower the biological variations; and secondly, by increasing the SNR (over a single voxel’s - compare the spectra in Fig. 1 with Fig. 3) to reduce the instrumental noise as (the number of voxels)^½. Together they yield T₁s at 5–10% regional CVs (see Table 2), suggesting that additional measurement in these structures in more animals (at similar spatial resolution and time) is unlikely to yield significantly different values.

Finally, it is noteworthy that although several minor metabolites, most notably myo-inositol, could also be detected at the TE=42 ms used (cf. Fig. 3), we focused only on the three major singlets. The motivation was to balance the dependence of the precision at which B₁ and T₁ are estimated on the voxel SNR (15), with the spatial resolution sought and total experiment duration. Specifically, the minor metabolites’ SNRs are fivefold to an order of magnitude lower than the main singlets. Even if their T₁s are fortuitously close to T₁^tune of NAA, Cho and Cr; at 180 μL resolution and ~4 hours of acquisition their inferior SNRs would lead to unsatisfactory precision.

Conclusion

Combining 3D ¹H-MRS with an optimized acquisition protocol makes for efficient use of four hours to map regional brain metabolites’ T₁s. The results reveal that these T₁s are sufficiently reproducible and that their variations among WM and GM structures in healthy rhesus macaques are small enough that use of a global average T₁ for each metabolite is justifiable for metabolic quantification. The overlap of the T₁ histograms of these metabolites indicates that they are probably characteristic to within very few percent making individual measurements unnecessary.