Neural computations underlying depth perception

Summary

Neural mechanisms underlying depth perception are reviewed with respect to three computational goals: determining surface depth order, gauging depth intervals, and representing 3D surface geometry and object shape. Accumulating evidence suggests that these three computational steps correspond to different stages of cortical processing. Early visual areas appear to be involved in depth ordering, while depth intervals, expressed in terms of relative disparities, are likely represented at intermediate stages. Finally, 3D surfaces appear to be processed in higher cortical areas, including an area in which individual neurons encode 3D surface geometry, and a population of these neurons may therefore represent 3D object shape. How these processes are integrated to form a coherent 3D percept of the world remains to be understood.

Introduction

We perceive our world in three dimensions. Most of us pay little attention to this fact in everyday life, but the difference between two-dimensional (2D) and three-dimensional (3D) vision is unmistakable when we see dinosaurs jump out of the flat screen at a 3D movie theater. The question of how the brain achieves 3D percepts from the 2D images formed on the retinae of the left and right eyes is a fascinating but complex one to answer. One of the most important visual cues for depth perception is binocular disparity [1,2], the difference in position between corresponding features in the left and right eye images of an object. Binocular disparity (Box 1) arises from the difference in the vantage points of the two eyes due to their horizontal separation. While there is no doubt that binocular disparity plays a major role in 3D vision, depth perception is not just about computing disparity at every location in a pair of images; it is about understanding spatial relationships among objects at different depths and recognizing objects by their 3D shapes. In this article, we review recent progress in our understanding of the neural mechanisms for depth perception with respect to three computational goals: determining surface depth order, gauging depth intervals, and representing 3D surface geometry and object shape.

Box 1. Terminology.

Binocular disparity

Due to the fact that we have two eyes facing forward and displaced horizontally, the image of an object located in front of or behind the point of visual fixation projects to slightly different locations on the retinae of the two eyes. Binocular disparity is the difference between the position of an image feature in one eye and that of the corresponding image feature in the other eye (see Fig. Ia). Although binocular disparity generally has both horizontal and vertical components, it is the horizontal component (i.e., horizontal disparity) that carries information about the depth of an object relative to the fixation point. In contrast, the vertical component (i.e., vertical disparity) arises when an object outside the plane of regard (the plane that contains visual axes of the two eyes) is viewed eccentrically, such that it is closer to one eye than to the other eye. Vertical disparities vanish when an object, regardless of its location in depth, is equidistant to both eyes (i.e., on the median plane) or on the plane of regard. Here we use the term binocular disparity to mean horizontal disparity.

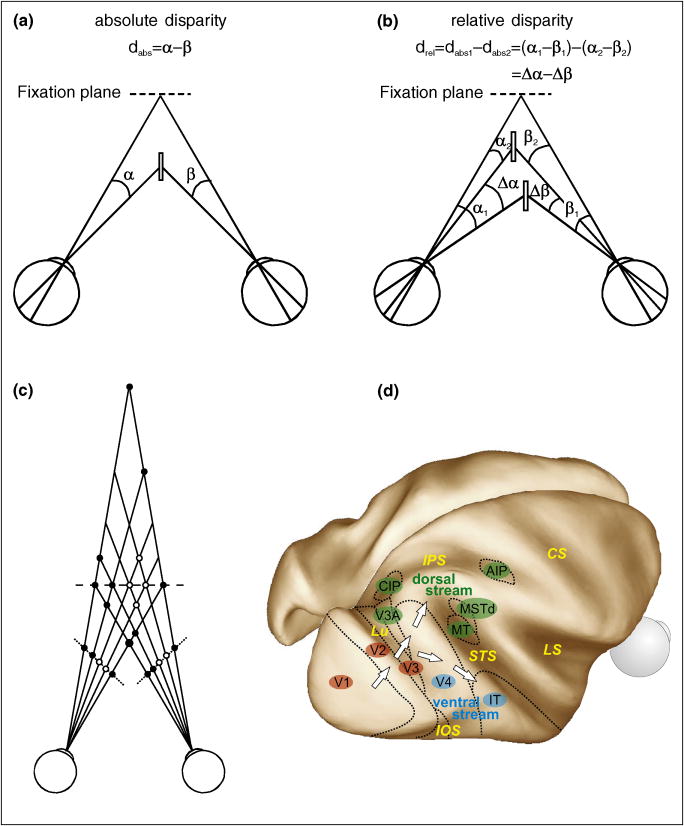
Absolute disparity

Absolute disparity (d_abs) is defined as the angular subtense of an image with respect to the point of fixation in one eye (α) minus that in the other eye (β) (Fig. Ia). Absolute disparity depends on the vergence angle of the eyes and therefore is useful for locating objects in 3D space and driving vergence eye movements to bring objects of interest into central fixation.

Relative disparity

Relative disparity (d_rel) is a difference between two absolute disparities (d_abs1 and d_abs2) (Fig. Ib). Relative disparity is independent of vergence angle and is believed to be important for fine depth discrimination.

Correspondence problem and false matches

The visual system needs to determine which part of the image in one eye corresponds to which part of the image in the other eye. This is called the correspondence problem. If the visual system had to solve this problem by matching local image features between the two eyes, there would be many possible (false) matches other than the correct ones. For example, black and white dots located at a constant depth along the dashed horizontal line in Fig. Ic would create monocular images depicted along dotted lines. However, there are many black and white dots at various locations in depth other than those along the horizontal dashed line that are consistent with local features in this pair of monocular images. The visual system must reject these false matches.

Dorsal and ventral processing streams

Two major projections originate from occipital cortex; one travels dorsally toward the parietal lobe and the other runs ventrally toward the temporal lobe (Fig. Id). Lesions in parietal cortex cause impairments in visuo-spatial cognition as well as visually guided action, whereas damage to temporal cortex leads to deficits in visual identification and discrimination performance [26-28].

The visual environment is typically filled with objects. Inevitably, views of some objects are occluded by others. Depth ordering is a process by which the visual system computes the depth arrangement of visible surfaces. When the visual system computes depth order, it also assigns depth intervals between surfaces. This gives a sense of volume to the impression of the world, the hallmark of depth perception. The ultimate goal of visual perception, however, is to recognize objects. To accomplish this, the visual system needs to deduce the shape of objects by first computing 3D surface geometry and then representing objects according to their 3D shapes independent of viewpoint.

Depth ordering

Determining which surfaces lie in front of others is a crucial step in understanding 3D scene structure. Interestingly, this process is operational for 2D image analysis, i.e. 2D scenes are interpreted in 3D terms [3]. The Kanizsa triangle [4] is a good example. When pacman-like shapes and V-shaped lines are arranged as shown in each panel of Fig. 1a, an illusory white triangle is perceived as an occluder lying on top of black disks and a second upside-down triangle outlined in black (as if they are arranged in depth, as depicted in Fig. 1b). This figure illustrates three phenomena that are crucial for understanding depth ordering: modal contour completion, amodal contour completion, and border ownership. Modal contour completion connects aligned luminance edges with an illusory contour that is associated with an occluding surface (the white triangle), whereas amodal contour completion connects aligned luminance edges with an invisible contour that is associated with an occluded surface (black disks and the second triangle). Border ownership refers to the assignment of edges or borders to the surface that is perceived as being in the foreground (the straight edges of the pacman-like shape belong to the white triangle, not the pacman). These three phenomena are closely related to the process of surface depth ordering.

Figure 1.

The Kanizsa triangle. (a) Three panels are shown for stereo viewing by free fusion. Adapted from [4] with permission of ABC-CLIO, LLC (Copyright © 1979 by Gaetano Kanizsa). Each of the panels viewed alone (non-stereo viewing) produces a percept of a white triangle lying on top of three black disks and a second upside-down triangle outlined in black. The white triangle is illusory, yet its contours are sharp and the interior of the triangle appears slightly brighter than the background. The Kanizsa triangle displays three phenomena. (1) Modal contour completion: the white triangle is formed by illusory contours extended from the straight, real luminance edges of pacman-like shapes. (2) Amodal contour completion: the V-shaped lines are extended behind the white triangle to form the second triangle. The arced edge of each pacman-like shape is also extended to form a disk. In either case, the extended contours are not visible as if they are occluded by the white triangle. (3) Border ownership: the straight edges of the pacman shapes, as well as the illusory contours that run over the second triangle, appear to belong to the white triangle. (b) When the figure in (a) is viewed stereoscopically to introduce a near disparity to the white triangle (either by diverging the eyes—fixating behind the figure—to fuse the left and middle panels or by converging the eyes—fixating in front of the figure—to fuse the middle and right panels), the white triangle appears to float above the rest of the figure as depicted here. The illusory contours now appear sharper, and the occlusion is more compelling. (c) On the other hand, when a far disparity is introduced to the white triangle (by fusing the remaining panel with the middle one in (a)) so that the white triangle lies explicitly behind the rest of the figure, it is now the white triangle that appears to be occluded. The figure appears as if we are looking at a white wall with three circular holes and V-shaped slots in it, and behind the wall is a white triangle on a dark background as depicted here. The white triangle is now formed by amodal contours that connect its tips (the straight edges of pacman-like shapes). The contour of each circular hole consists of real (the arced portion of the pacman shape) and illusory (modally completed) portions, both of which belong to the white wall.

Not surprisingly, binocular disparity can powerfully modulate contour completion and border ownership [3]. When the Kanizsa triangle is viewed stereoscopically (by free fusing the left and middle panels or the middle and right panels in Fig. 1a), the locations of modal and amodal contours and border ownership change depending on the sign of binocular disparity (i.e., near or far) applied to the white triangle, and the perceived depth order changes accordingly (compare Fig. 1b to Fig. 1c). In other words, binocular disparity dictates surface depth order by determining the locations of contours as well as surfaces to which the contours belong, so that the perceived surface arrangement is consistent with that of nearer surfaces occluding farther surfaces.

How does the visual system compute depth order? Specifically, what are the neural substrates for modal and amodal contour completion and how is border ownership encoded? Several studies have addressed these questions. Responses to both modal and amodal contour stimuli have been reported in early visual areas [5-8]. Neurons in extrastriate areas also show responses that are modulated by border ownership [9-12•]. Among these studies, of particular interest here are those that examined modulatory effects of binocular disparity.

Some orientation selective neurons in the primary visual cortex (V1) of monkeys have been shown to respond to amodally completed contours but only when an occluding patch was placed at a near depth [7] (Fig. 2a). On the other hand, Bakin et al. [8] found that many neurons in V2, but few in V1, showed response facilitation to amodal contour stimuli when an occluding patch was at a near depth. These results indicate that neurons in early visual areas can signal amodal contour completion when the occluding surface appears in front of the real contours that are amodally connected behind the occluder. Bakin et al. [8] also examined neural responses to modally completed contours at a near depth, and found that roughly one third of disparity-selective V2 neurons, but only one V1 neuron, showed responses consistent with modal completion (Fig. 2b).

Figure 2.

Modal and amodal contour responses and border ownership selectivity. (a) Peri-stimulus time histograms (PSTHs) of responses of an orientation selective neuron from monkey V1 to the stimuli depicted above each PSTH. The neuron responded to an elongated bar stimulus presented over the receptive field, but did not respond to two unconnected bar segments placed outside the receptive field either with or without a patch covering the receptive field. However, the neuron responded when the patch was placed at a near depth to facilitate amodal contour completion, but not when the patch was placed at a far depth, which does not induce amodal contours. Adapted from [7] with permission (Copyright © 1999 by Macmillan Publishers Ltd.). (b) Responses of a monkey V2 neuron to various stimuli depicted below each bar graph. The left panel shows the disparity tuning of this neuron measured with an elongated bar (the dashed square represents the receptive field). The right panel shows responses of the neuron to various combinations of two bar segments placed just outside the receptive field and a rectangular patch over the receptive field. The neuron did not respond to these stimuli except when the two bar segments were presented at a near depth to induce modal contour completion. Reproduced from [8] with permission (Copyright © 2000 by Society for Neuroscience). (c) Raster plots for responses of a V2 neuron to various figure-ground stimuli. The black oval in each stimulus depiction indicates the receptive field. In each row, the stimulus within the receptive field is identical but the location of the square patch (defined by a difference in luminance or disparity) relative to the receptive field is different. This neuron responded whenever the luminance-defined figure resided on the left side of the receptive field (i, iii) or whenever the surface on the left side of the receptive field was in front (v, vi), suggesting that it can signal border ownership assignment to the left regardless of the stimulus cues defining the border. Reproduced from [11] with permission (Copyright © 2005 by Elsevier Inc.).

There is also some evidence that neurons encode border ownership based on various cues including binocular disparity (e.g. [10,11••]). Zhou et al. [10] reported that 18%, 59%, and 53% of neurons that they examined in V1, V2, and V4, respectively, showed response modulation depending on whether a luminance edge presented over the receptive field was a part of a figure located on the right or the left side of the receptive field, indicating that they could signal border ownership. Subsequently, Qiu and von der Heydt [11••] showed that border ownership responses of V2 neurons to figures defined by binocular disparity were similar to those defined by luminance contrast (Fig. 2c), suggesting that responses of V2 neurons represent borders as edges of surfaces.

These studies suggest that neural computation of depth order begins in early stages of visual cortical processing. Neurons in V2 in particular seem to be involved in determining where contours and surface borders lie in 3D space and thus the depth order. These findings provide important clues as to where surface representations are established in the brain, a key early step in constructing a 3D percept of the world[13]. As mentioned earlier, depth order is determined for 2D images as well even though one would not experience a sense of volume in between surfaces. This means that the visual system must assign appropriate depth intervals between surfaces whenever binocular disparity (or motion parallax) cues are available. Next, we consider studies that examine where depth intervals are computed.

Depth intervals

In addition to playing a major role in depth ordering, binocular disparity creates a vivid sense of 3D volume between points having different disparity values. One can easily experience this by viewing a scene with one eye vs. two eyes. It is also intriguing to notice that the 3D space between objects at different depths does not appear to change depending on where you fixate your eyes in depth. Since the binocular disparity of an individual point relative to the fovea (absolute disparity, Box1) varies with fixation distance while the difference in binocular disparity between two points (relative disparity, Box1) does not, our perception of depth is thought to depend heavily on relative disparities rather than absolute disparities. It has been known for some time that humans and animals are far more sensitive to variations in relative disparity compared to absolute disparity [14-16], which suggests that the visual system computes relative disparity and makes it available for depth discrimination.

To identify where relative disparity is computed in the brain, tuning for relative disparity of single neurons in various cortical areas has been studied. In V1, neurons appear to signal absolute disparity [17], and similar results were found in the middle temporal area (MT) [18]. In contrast, Thomas et al. [19] found that a small number of neurons in V2 exhibit selectivity for relative disparity while others show partial selectivity and many also signal absolute disparity. In area V4, neurons show a greater degree of relative disparity selectivity including a substantial minority that are fully selective for relative disparity [20•].

Among the areas at early stages of visual cortical processing, V3 and V3A have not yet been considered. These areas are of particular interest since functional Magnetic Resonance Imaging (fMRI) studies in both humans and monkeys have implicated their involvement in stereoscopic analysis and have suggested that these areas may be involved in coding relative disparities [21-23]. Recent preliminary results from our laboratory (Anzai et al., abstract in Soc Neurosci Abstr 2008, 462.10) suggest that many neurons in V3 and V3A carry only absolute disparity information, with a minority that are biased toward relative disparity selectivity, roughly comparable to results from V2 [19]. It is currently unclear why fMRI results suggest strong relative disparity signals in V3A (e.g. [22]), whereas our single-unit studies do not. Overall, these studies suggest that computation of relative disparity may gradually emerge along the ventral stream (toward V4, Box1), while the dorsal stream (toward V3A/MT, Box1) carries mostly absolute disparity information [24] (see also [25•]). This dichotomy may be a reflection of absolute disparity being useful for driving vergence eye movements and relative disparity being useful for fine depth judgments [24], and is consistent with the notion that the dorsal stream is involved in visually guided action whereas the ventral stream is involved in perceptual identification of objects [26](see also [27,28]).

However, these results should be interpreted with some caution. The neurophysiology studies mentioned above used a center-surround stimulus configuration in which the disparity of the center stimulus (which covered the classical receptive field) was varied to measure the neuron's tuning for each different disparity value that was applied to the surrounding annulus (but see [17]). Therefore, these studies generally assumed that the computation of relative disparity involves a center-surround receptive field organization. However, relative disparity could be computed in ways that are not well characterized by these stimuli. For example, von der Heydt et al. [29] showed that some neurons in V2 respond to stereoscopically defined edges within the classical receptive field and are selective for edge orientation, suggesting that they signal disparity differences within the receptive field (see also [30]). It is possible that relative disparity selectivity could be substantially more robust if measured with different stimulus configurations. In fact, one could design many different stimuli that contain relative disparity, such as slanted, curved, or corrugated surfaces to name a few, and use them to test relative disparity selectivity of neurons. However, such an approach has its own drawback; relative disparity and surface geometry are confounded in these stimuli and as a result it is hard to distinguish true relative disparity selectivity (independent of stimulus configurations) from surface shape selectivity (independent of shape cues such as texture and disparity gradients, but not of stimulus configurations). Thus, a fuller understanding of relative disparity coding may require new methods that provide a more general characterization of the underlying operations without assuming a specific stimulus configuration.

From a computational point of view, it may be more efficient to compute relative disparity after the stereo correspondence problem is solved to avoid confounds of false matches (Box 1). Responses of binocular neurons in V1 signal a local image correlation between the two eyes [31,32] and are prone to respond to false matches [33]. If relative disparity is computed from the V1 output without first solving the stereo correspondence problem, results of the computation may be contaminated by false relative disparities. There is evidence that the stereo correspondence problem is largely solved in later stages of the ventral stream, including V4 [34] and the inferior temporal area (IT) [35]. If that is indeed the case, then it may make sense for relative disparity signals to more strongly emerge in V4 where Umeda et al. [20•] found a substantial proportion of neurons showing complete selectivity for relative disparity. This may also be the stage at which 3D surface representations start to become more fully established. Next, we examine recent progress in understanding neural mechanisms for 3D surface geometry and object shape representations.

3D surface geometry and object shape

Surfaces found in natural scenes often have complex geometry. It is a challenging task for the visual system to compute 3D surface geometry, but it is also necessary for recognizing objects by their shapes. What kind of response properties does one expect from neurons that are involved in representing surface geometry? Clearly, they must be selective for visual cues that vary with surface geometry. This includes spatial gradients in binocular disparity, texture, and velocity, among other cues. If neurons are truly selective for 3D surface geometry, then their selectivity should be consistent across different cues that define the same surface geometry (cue-invariance). In addition, their selectivity should tolerate variations in the position, scale, and mean depth of the surface.

Neurons selective for 3D planar surface orientation have been found in multiple cortical areas along both dorsal and ventral streams (see Fig. Id of Box 1 for a map of cortical areas discussed here). In the dorsal stream, MT neurons are selective for 3D surface orientation defined by velocity gradients [36,37] and binocular disparity gradients [38]. Nguyenkim and DeAngelis [38] showed that tuning for the tilt of planar surfaces was generally insensitive to changes in the mean disparity of the stimuli, suggesting that some MT neurons are indeed selective for disparity gradients (see [39] for caveats). In the dorsal medial superior temporal area (MSTd), to which MT projects, most neurons are selective for 3D surface orientation defined by velocity gradients with tolerance for variations in position [40], though it is not known if they are also selective for 3D surface orientation defined by disparity gradients. Within the intraparietal sulcus, the caudal intraparietal area (CIP) contains many neurons that are selective for 3D surface orientation whether it is defined by texture gradients, disparity gradients, or linear perspective cues [41,42], demonstrating some degree of cue-invariance. Neurons selective for curved surfaces (convex vs. concave) are also found in CIP [43]. Similarly, neurons in the anterior intraparietal area (AIP) exhibit selectivity for 3D shapes including slanted and curved surfaces [44].

Figure I.

(a) Absolute disparity. (b) Relative disparity. (c) Correspondence problem and false matches. (d) Cortical areas and two major visual processing streams. Locations of cortical areas described in this article are mapped onto a postero-dorso-lateral view of a partially inflated macaque brain (Caret Software 5.61 http://brainvis.wustl.edu/caret), to expose visual areas that lie within sulci. Dotted lines indicate approximate areal boundaries. Early visual areas (V1, V2, and V3) are marked by red ovals, whereas areas that are considered to belong to the dorsal stream (V3A, MT: middle temporal, MSTd: dorsal medial superior temporal, CIP: caudal intraparietal, and AIP: anterior intraparietal) and the ventral stream (V4, IT: inferior temporal) are indicated by green and blue ovals, respectively. Major sulci are labeled in yellow (CS: central sulcus, IPS: intraparietal sulcus, IOS: inferior occipital sulcus, LS: lateral sulcus, Lu: lunate sulcus, STS: superior temporal sulcus).

In the ventral stream, Hinkle and Connor [45] measured 3D orientation selectivity of neurons in V4 and found that a majority of neurons tuned to 2D bar orientation were also selective for bar orientation in depth. Many of these neurons showed selectivity that was tolerant to variations in position and mean depth. For a subset of these neurons, 3D surface orientation selectivity was also measured using stimuli defined by disparity gradients, but only one neuron exhibited selectivity. However, since these neurons were first screened for 2D orientation selectivity, it is possible that neurons selective for disparity gradients were missed. In contrast, Hegde and Van Essen [46] found that some V4 neurons show 3D orientation selectivity for disparity gradients, but they did not test for position or depth invariance. Neurons in IT exhibit cue-invariant surface orientation selectivity [47], with similar 3D orientation preferences for texture- and disparity-defined surfaces. In addition, IT neurons are selective for 3D shape of curved surfaces, and show position and size tolerance to these variations [48-50]

These results indicate that at least simple surface geometries, such as oriented planes and convex and concave surfaces, are represented in the mid- to high-level cortical areas in both dorsal and ventral streams. However, the ultimate goal of visual perception is to recognize objects, which often have more complex surface geometries. How does the visual system represent complex 3D shapes? One possibility is that downstream neurons combine these simple 3D surface representations to create more complex representations of object shape.

A recent study by Yamane et al. [51••] suggests that the visual system may indeed take such an approach. Using an evolutionary stimulus generation algorithm that morphs stimuli iteratively based on neural responses, they were able to characterize the selectivity of IT neurons for more complex 3D shapes. They found that IT neurons were selective for 3D spatial arrangements of surface fragments specified by their 3D orientation and curvature (Fig. 3a). Neurons maintained their 3D shape selectivity as long as binocular disparity or shading cues were present in the display, although texture gradient cues alone were not sufficient for some neurons (Fig. 3b). Remarkably, selectivity was largely independent of various shading patterns created by changes in lighting direction (Fig. 3c), and was tolerant to variations in stimulus position, size, and depth (Fig. 3d,e), suggesting that IT neurons truly represent 3D surface geometry. However, IT responses were not so tolerant to stimulus rotation (Fig. 3f). This suggests that the 3D shape representation by individual IT neurons is not entirely in an object-centered frame of reference, which is consistent with some psychophysical and physiological evidence that object representations are viewer-centered [52] and with the notion that view-invariant object recognition is achieved by pooling responses of view-tuned neurons encoding many different views of an object [53].

Figure 3.

Tuning of an IT neuron for 3D surface geometry. Reproduced from [51••] with permission (Copyright © 2008 by Macmillan Publishers Ltd.). (a) The most effective stimulus for this neuron is shown. It was obtained after eight generations of stimulus evolution based on the neuron's responses. (b) The neuron responded well as long as the 3D shape of the stimulus was defined either by binocular disparity or shading cues, thus exhibiting some degree of cue-invariance. Texture cues alone were not sufficient for this neuron. (c) Variations in shading pattern produced by changing the lighting direction along the horizontal (black curve) or vertical (green curve) direction did not affect the neuron's response. (d) The response was largely independent of stimulus position in depth. (e) Stimulus size also did not affect the response. (f) Rotation of the stimulus about the x-axis (black) and y-axis (green) strongly suppressed the response, while rotation about the z-axis (blue) was tolerated over a range of about 90°.

Conclusions

Depth perception involves various complex computations. In this review, we focused on three critical components of these computations. Mounting evidence suggests that early visual areas, V2 in particular, play an important role in depth ordering through mechanisms of contour completion and border ownership assignment. Depth intervals, encoded in the form of relative disparities, are most likely represented at intermediate to higher stages of visual processing, and V4 seems to be a prime candidate. Finally, higher cortical areas are involved in representing complex 3D surfaces, and individual neurons in IT appear to represent surface geometry in terms of 3D spatial configurations of simple surface segments that are defined by 3D orientation and curvature. However, this representation appears to be viewer-centered, and 3D object shapes may be represented by a population of IT neurons through a learning process to associate multiple views of the same object [54].

It remains to be seen how these computational processes come together to form a coherent 3D percept of the world. One key component that binds these processes is surface representation. The depth ordering process may need to occur before surface representations are established, and depth intervals (relative disparities) may not be fully available until surface representations are created. Needless to say, complex object shapes are derived from local surface representations. Therefore, understanding neural substrates of the viewer-centered representation of visible surfaces, which Marr called the 2½-D sketch [13], may hold the key to understanding the neural mechanisms of depth perception.