Adaptive Switches in Midbrain Circuits

Abstract

In this issue of Neuron, Mysore and Knudsen (2012) describe a simple, anatomically supported circuit that can categorize stimuli into “strongest” and “others,” regardless of their absolute strength. Such flexible categorization cannot be achieved by lateral inhibition alone but also requires that the inhibitory neurons reciprocally inhibit each other.

Selecting the most relevant stimulus in the environment is one of the key elements of behavior. It can be argued that this process begins already in early sensory systems where stimuli are transformed to emphasize their most unexpected features (Gollisch and Meister, 2010), such as differential motion (Lettvin et al., 1959; Olveczky et al., 2003) or deviations from an anticipated trajectory (Berry et al., 1999) or from expected second-order stimulus correlations (Sharpee et al., 2006). Many of these complex computations come about through the interplay of lateral inhibition (also called “surround suppression”) and response normalization—two features of neural circuitry that are observed almost universally in different neural systems (Olsen et al., 2010; Carandini et al., 1997; Reynolds and Heeger, 2009).

In some cases, stimuli can be usefully categorized using predetermined boundaries (Prather et al., 2009). Often, however, these boundaries need to be defined in relative terms, by separating stimuli into the “strongest” and “others” (Mysore and Knudsen, 2011). The article by Mysore and Knudsen in this issue of Neuron argues that such flexible categorization cannot be achieved by lateral inhibition alone and suggests that reciprocal inhibition between neurons that mediate lateral inhibitory connections is one of the simplest and most robust ways of solving this task (Mysore and Knudsen, 2012).

To gain an intuition for why reciprocal inhibition is necessary, we will follow the authors in considering model circuits with two inputs and two outputs (Figures 1 and 2). This circuit’s task is to signal which of the two inputs is the strongest. Empirically, responses to a single input are nonlinear, saturating for strong inputs. They are well fit by sigmoidal functions, which is also expected on theoretical grounds when a function is minimally constrained to relate inputs to outputs (Fitzgerald et al., 2011). We will assume that all neurons in this circuit respond this way to their inputs.

Figure 1. A Circuit with Lateral Inhibition Can Produce Switch-like Responses with Constant Threshold Value.

The circuit diagram is shown on the left. Input and output neurons are marked with circles; diamonds mark inhibitory neurons. Right: the responses of output 1 are plotted as a function of “competitor” input 2, for different values of input 1 (corresponding to the stimulus strength within the receptive field). The switch between high and low values of output 1 occurs for the same value of competitor input 2, regardless of input 1. Input and output strength are in arbitrary units.

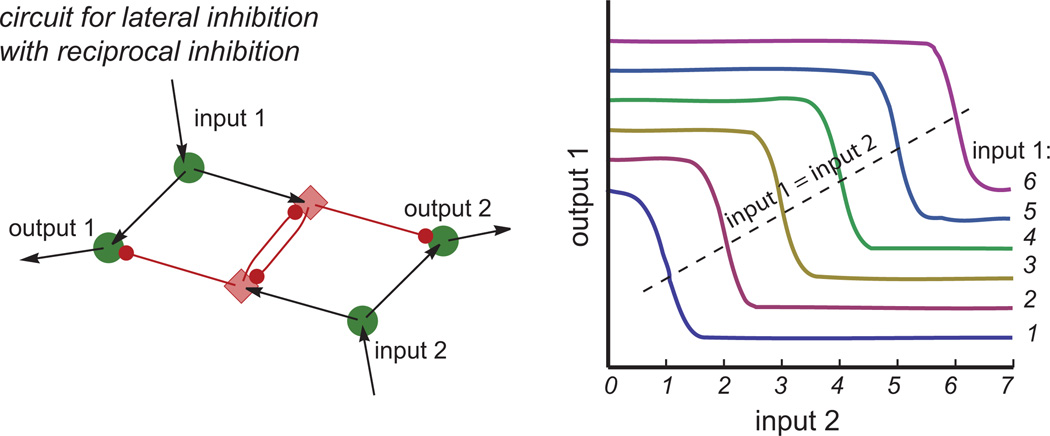
Figure 2. A Circuit with Reciprocal Inhibition of Feedforward Lateral Inhibition Can Produce Adaptive Switch-like Responses.

Notations are as in Figure 1. The main difference is the switch from low to high level in output 1 occurs when “competitor” input 2 exceeds the “main” input 1.

A circuit that includes lateral inhibition (Figure 1) can yield switch-like responses in output 1 when the strength of input 2 is increased beyond a certain value. However, the threshold value does not depend on input 1. In other words, this categorization is defined in absolute terms and does not encode the relative strength of the two inputs. In contrast, a circuit where inhibitory “interneurons” also inhibit each other produces switch-like responses (Figure 2), with thresholds that increase with the strength of input 1. Thus, this simple elaboration of the circuit is sufficient to produce switch-like responses that reflect the relative strength between the two inputs, producing nearly constant large responses to a stronger input and also nearly constant small responses to a weaker input. It is noteworthy that output responses to a weaker input are not driven to zero but remain proportional to that weak input, as observed experimentally in the intermediate and deep layers of barn owl’s optic tectum (superior colliculus in mammals). This circuit behavior is in contrast to properties of winner-take-all model circuits where all information about the strength of the weaker input is abolished.

The addition of reciprocal inhibition to the lateral inhibition circuit is the simplest modification that can yield adaptive switch-like responses. More complex schemes are certainly possible, but they typically are less robust and require longer times to reach the equilibrium, as Mysore and Knudsen (2012) demonstrate. They also show that their circuit model reproduces a range of other more subtle features in the experimental data. For example, the reciprocal inhibition circuit can, for some values of parameters, produce the sharpening of the transition between the two output states when input strength is increased (such sharpening is illustrated in Figure 2, cf. lower curves for input strength equal to 1 and upper curves for input strength equal to 6). Such sharpening was indeed observed experimentally by Mysore and Knudsen (2012) in some neurons. Another feature of the data is the presence of stronger suppression of responses to the weakest than to the strongest input. This feature was also accounted for by the reciprocal inhibition circuit. Finally, this circuit is supported by anatomical studies. Neurons in a midbrain GABAergic nucleus, the nucleus isthmi pars magnocellularis, receive input from retinorecipient layers of the optic tectum and send broad projections to the intermediate and deep layers (which would provide support for lateral inhibition) as well as within the nucleus itself (Wang et al., 2004). The latter set of connections would provide a way to implement reciprocal inhibition.

The importance of the lateral inhibition circuit motif has been appreciated in a variety of sensory systems (Carandini et al., 1997; Olsen et al., 2010). The functional implications of reciprocal inhibition between inhibitory neurons have been studied primarily with respect to decision making (Miller and Wang, 2006; Machens et al., 2005). Functional implications of reciprocal inhibition in sensory coding have been less explored, but see the recent report on the role of the “giant” GABAergic interneuron for generating sparse coding in olfaction (Papadopoulou et al., 2011). The findings of Mysore and Knudsen (2012) raise the possibility that reciprocal inhibition of feedforward lateral inhibition might also play an important role in sensory systems. First, anatomical support for reciprocal inhibition is found in other brain areas, such as the thalamic reticular nucleus. Second, while switch-like neural responses are crucial for categorization, they are observed only in a minority of neurons in optic tectum, with most neurons exhibiting much more gradual normalization of responses. So far, the more gradual neural responses have been the focus of normalization models in sensory coding. Perhaps, a closer look at sensory coding will also reveal the presence and functional significance of such switch-like responses here.