Mechanically-guided deterministic assembly of 3D mesostructures assisted by residual stresses

Abstract

Formation of three-dimensional (3D) mesostructures in advanced functional materials is of growing interest due to the widepread envisioned applications of devices that exploit 3D architectures. Mechanically-guided assembly based on compressive buckling of 2D precursors represents a promising method, with applicability to a diverse set of geometries and materials, including inorganic semiconductors, metals, polymers and their heteogenous intergration. This paper introduces ideas that extend the levels of control and and the range of 3D layouts that are achievable in these systems. Here, thin, patterned layers with well-defined residual stresses influence the process of 2D to 3D geometric transformation. Systematic studies through combined analytical modeling, numerical simulations and experimental observations demonstrate the effectiveness of the proposed strategy through ~20 example cases with a broad range of complex 3D topologies. The results elucidate the ability of these stressed layers to alter the energy landscape associated with the transformation process and, specifically, the energy barriers that separate different stable modes in the final 3D configurations. A demonstration in a mechanically tunable micro-balance illustrates the utility of these ideas in a simple structure designed for mass measurement.

Graphical Abstract

A mechanically-guided approach assisted by residual-stress-induced bending enables deterministic assembly of 3D mesostructures with complex topologies, including those inaccessible previously. Combined theoretical and experimental studies elucidate the underlying mechanics of physics and materials aspects, in a way that establishes quantitative design diagrams in terms of key parameters. This approach has the potential to be broadly useful in 3D microsystems technologies.

1. Introduction

Three-dimensional (3D) micro/nanostructures are growing interest, owing to their potential applications in areas from metamaterials,^[1–7] to biomedical sensing devices,^[8–16] to microelectromechanical components,^[17] to energy storage systems,^[16,18–25] to electronics,^[26–33] and to photonics and optoelectronics.^[34–37] 3D mesostructures in advanced materials can be achieved using methods such as printing/writing,^[38–41] fluidic self-assembly,^[42,43] and templated growth.^[44–47] Although these approaches offer many attractive featuers, most require specially designed materials,^{[38–40,48–50]} and they cannot be used directly with many advanced functional materials of interest (e.g., single-crystalline semiconductors). Other routes that exploit capillary forces,^[51–53] residual stresses,^[54–60] or origami-inspired reconfigurable designs^[61–64] offer compatibility with established planar device technologies. The former two are irreversible and have limited control over critical parameters such as the folding angle;^[14,65–70] the latter one has been applied to certain classes of geometries such as polyhedrons, tubes and variants of these.

Methods based on compressive buckling^[29,71–73] can transform 2D precursors built with nearly any class of thin film materials, including those used in the electronics and optoelectronics industries, into tunable 3D structures with diverse topologies. The process occurs in a parallel fashion at high throughput, over length scales from sub-micron to several centimeters. The 2D-to-3D transformation involves not only in- and out-of-plane translations and rotations, but also mechanical deformations dominated by out-of-plane bending and twisting, by design of the characteristics of the 2D precusors.^[29,73,74] In most reported cases, unique 3D geometries result by consequence of strain energies in the first-order buckling modes (i.e., energetically the most probable configuration) that are much lower (e.g., by a factor of 2) than those of all other modes.^[29] For certain complex 2D precusors, particularly those that yield 3D geometries with multilevel features, the strain energies of first- and second-order (or higher-order) modes can be sufficiently similar to allow controlled access to a selected mode by use of external perturbation. The ideas introduced here exploit patterned thin films with well-defined residual stresses, incorporated at strategic locations in the 2D precursor, as a means for this selection to achieve high-order (≥ 2) buckling modes unobtainable previously, or for reconfiguration of local regions to achieve topologies qualitatively different from any of the buckling modes. The addition of these stress-controlling layers also can eliminate near degeneracies that sometimes occur between the lowest order mode and other modes of complex 3D configurations, thereby enhancing the yields in realizing targeted outcomes. The following introduces the underlying mechanics issues through combined analytical modeling, numerical simulations and experimental measurements. Demonstrations include a broad set of 3D mesostructures, each achieved using quantitative modeling/simulations to guide the choices of stresses and geometrical layouts of the control layers. An application in a mechanically tunable micro-balance device serves as a simple example of the utility of these strategies in mass measurement of microscopic particles.

2. Results and Discussion

2.1 Fabrication scheme and design principle

The overall approach for mechanically-guided assembly of 3D mesostructures is similar to that reported recently,^[29,71] in which 2D precursors typically formed by methods of semiconductor processing bond at selected locations onto pre-stretched elastomer substrates. The 3D structures result from coordinated motions induced by release of prestrain in the elastomer. For cases reported here, the precursors and bonding sites consist of photodefinable epoxy (SU8, thickness = 1.5 – 7 μm) and silicon oxide (thickness = 50 nm, via electron-beam evaporation). Patterned sacrificial layers (AZ 5214, thickness = 1.4 μm) that are removed by immersion in acetone immediately prior to the buckling process ensure that the non-bonding regions separate efficiently from the elastomer. Here, the major differences in fabrication between the current and previous studies are the preparation of thin films with well-defined residual stress, and the adhesion of the residual-stress layers with selective region of 2D precursor. The stress-controlling layers consist of thin films of SiNx deposited with either tensile or compressive residual stresses, and patterned into desired geometries on the top surfaces of the 2D precursors by photolithography and reactive ion etching with CF₄ gas (e.g., the 3D mesostructure shown in Fig. 1a). Plasma-enhanced chemical vapor deposition (PECVD) of the SiNx with control over parameters such as the direct current (DC) power, chamber pressure, gas flow rate and operational frequency allows formation of thin films with well-defined residual stresses ranging from + 480 to − 581 MPa (+ and − indicates tensile and compressive residual stress, respectively; See Figure S1, Supplementary Information for details). A thin layer of adhesive (Omnicoat®, Microchem) cast on top of the SU8 before photopatterning ensures strong bonding between the SiNx and SU8. Removing a layer of gold (thickness = 100 nm; electron beam evaporation; KI-I₂ etchant) on the silicon wafers that serve as substrates for the SU8 and the SiNx allows efficient release for transfer. Detailed fabrication procedures are in Figure 1a, Experimental Section, and Figure S2 (Supplementary Information).

Figure 1.

(a) Schematic illustration of steps for fabricating 3D mesostructures using controlled, compressive buckling assisted by residual stresses. (b) Results of experiment, analytical modeling and FEA predictions for the residual-stress assisted assembly from an H-shaped 2D precursor. Results of analytical modeling and FEA (middle three panels) describe the formation of the 3D mesostructure (SU8 and SiNx), along with corresponding SEM images (right most panel) of the final configuration. Scale bars, 1 mm.

Figure 1b presents an example of residual-stress assisted assembly of two-floor mesostructures from an H-shaped 2D precursor, whose base consists of a single layer of SU8 with uniform thickness (2 μm) and bonding sites indicated in red. SiNx resides only on top of the central ribbon (100 nm SiNx/2 μm SU8) to leverage the strain mismatch for controlling its bending direction during assembly. Compressive forces associated with release of the substrate prestrain (ε_pre = 80%) act in combination with those associated with the residual stresses in the SiNx to transform the 2D precursor into controlled 3D configurations. Intermediate states in the assembly process, denoted by the magnitude of released strain (Figure S3, Supplementary Information), can be obtained from finite element analysis (FEA) and analytical modeling (See Figure S4 and Supplementary Text, Supplementary Information for details), as shown in Figure 1b. When the SiNx layer has a sufficiently large tensile residual stress (e.g., + 480 MPa), the center ribbon tends to bend downward to minimize the strain energy. In contrast, this ribbon bends upward without the SiNx, or with a layer of SiNx that has compressive stress (e.g., − 580 MPa) or tensile stress below a certain threshold. In both cases, the final 3D configurations predicted by FEA or analytical modeling agree well with the scanning electron microcope (SEM) images from experiments.

The bending direction (up or down) can be controlled by the residual stress (σ_residual), the thickness (t_SiNx) of the SiNx, and the thickness (t_SU8) of the SU8. Figure 2a presents a design diagram in the space of σ_residual and t_SU8 for a given SiNx thickness (t_SiNx = 100 nm). Three different domains, denoted by “pop up”, “pop-down” and “unable to fully delaminate”, can be identified. Here, to achieve full delamination of the 2D precursor from the substrate, t_SU8 must be sufficiently large to provide separation forces that can overcome the Van der Waals interactions at the weak interface. Such Van der Waals interactions result mainly from the collapse of the freestanding 2D ribbons onto the substrate after removal of the thin sacrificial layers (1.4 μm). The critical thickness for full delamination, as represented by the red dashed line in Figure 2a, can be estimated quantitatively using an energetic analysis (See Figure S5 and Supplementary Text, Supplementary Information for details). FEA results define the boundary between the two different buckling modes, as shown by the blue solid line in Figure 2a. The minimum tensile residual stress necessary to achieve the pop-down buckling mode increases with increasing SU8 thickness. For small stresses, the pop-up buckling mode occurs. Experimental results based on precursors with various different geometries appear as circles (numbered from ‘1’ to ‘9’) in Figure 2a. Representative 3D configurations shown in the SEM images of Figure 2b agree well with the FEM predictions and the design diagram. The configurations of structures (points ‘8’ and ‘9’) that do not delaminate fully are sensitive to subtle properties of the interface with the substrate, and are therefore difficult to predict by modeling. Experiments and FEA indicate that the final 3D configurations for a given buckling mode (pop down or up) are insensitive to changes in σ_residual and t_SU8, for the ranges considered herein.

Figure 2.

(a) Design diagram in the space of residual stress (σ_residual) and SU8 thickness (t_SU8), for t_SiNx =100 nm. (b) SEM images and corresponding FEA predictions for 3D mesostructures with different design parameters as marked by the circles in (a). (c) Probability to achieve pop-down mode for 2D precursors with three different design parameters (corresponding to points ‘2’, ‘10’ and ‘11’ in (a)). Scale bars, 1 mm.

Even for parameters that correspond to the “pop-down” domain in Figure 2a, the pop-up mode is still possible, because it corresponds to a local minimum in the strain energy minimum, as detailed in the subsequent section. The variability likely arises from slight differences in experimental conditions, such as asynchronous release of the biaxial strain and/or parasitic adhesion/stiction at regions adjacent to the bonding sites. A statistical analysis > 30 based on observations from samples with, nominally, the same design parameters illustrates this effect. A representative set of results appear in Figure S6 (Supporting Information) for the design point ‘10’ (σ_residual = + 480 MPa and t_SU8 = 3.5 μm). The data indicate that the probability of the pop-down mode is ~ 49%. The results in Figure 2c show that the probability of the pop-down mode decreases sharply as the location of design parameter moves gradually from the domain of “pop-down” to “pop-up”.

2.2 Mechanics of buckling mode control

Energetic analyses capture the underlying mechanics of buckling mode control. Three representative examples have the design parameters (t_SU8, t_SiNx, σ_residual) = (3 μm, 100 nm, 480 MPa), (3.5 μm, 100 nm, 480 MPa) and (4 μm, 100 nm, 480 MPa), respectively, corresponding to points ‘2’, ‘10’ and ‘11’ in Figure 2a. All calculations use a prestrain ε_pre = 80%.

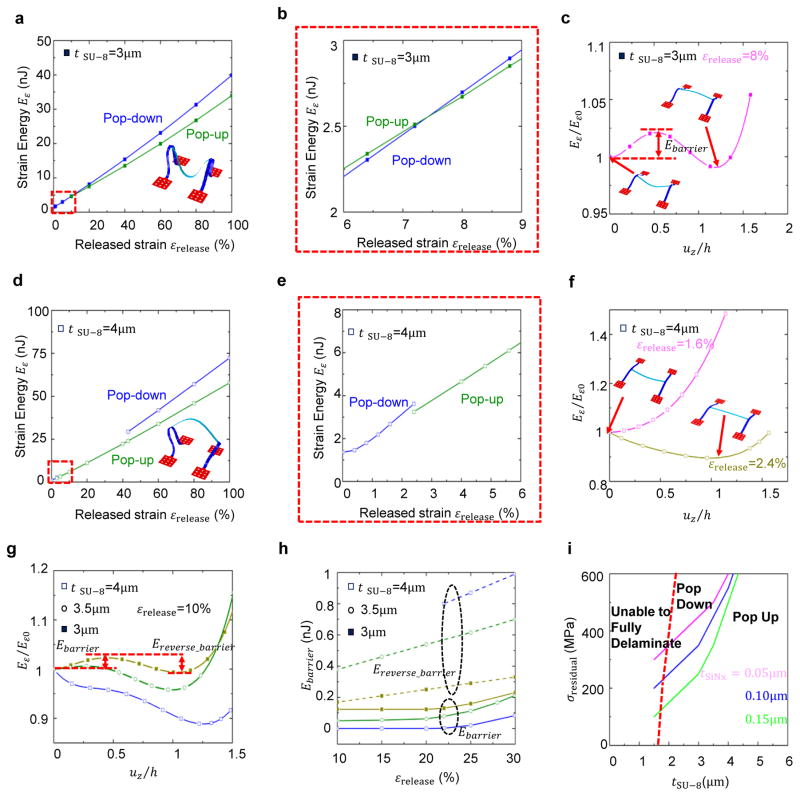
Figure 3a and b depicts the dependence of strain energy on the released strain (ε_release) for the case with design parameters (3 μm, 100 nm, 480 MPa). According to the result in Figure 2c, both pop-down and pop-up modes are possible with this set of parameters. The tensile residual stress in the SiNx layer, however, causes the pop-down mode to have a lower strain energy than the pop-up mode at the initial stage of strain release (e.g., ε_release = 0~7.5%). As a consequence, the structure tends to move into the pop-down mode. As the released strain increases beyond 7.5%, the strain energy of pop-down mode exceeds that of the pop-up mode. The buckling mode is, however, unable to transform into the pop-up mode, due to the existence of an energy barrier, as shown in Figure 3c and Figure S7 (Supporting Information). The magnitude of this barrier as a function of ε_release can be obtained by applying an out-of-plane displacement u_z at the middle point of the bilayer until the mode switches from pop-down to pop-up, as illustrated in Figure S7 (Supporting Information). During this process, the strain energy first increases to a maximum, and then decreases with increasing u_z, as shown in Figure 3c for ε_release = 8%. The difference between the maximum strain energy and the initial value for ε_release = 0% is simply the energy barrier (E_barrier) of interest. For design parameters (3 μm, 100 nm, 480 MPa), such a barrier exists during the entire process of strain release (Figure 3h). Here, the double energy wells result in two stable states. Nevertheless, due to an inability to overcome the energy barrier (E_barrier), the 3D structure maintains the pop-down mode as the released strain increases.

Figure 3.

Mechanics analyses of buckling mode control for the H-shaped 2D precursor. Strain energy of 3D structures with pop-up (blue) and pop-down (green) modes versus released strain, and the corresponding magnified view, for the design parameters (t_SU8, t_SiNx, σ_residual ) = (3 μm, 100 nm, 480 MPa) (a and b) and (4 μm, 100 nm, 480 MPa) (d and e). The insets of (a) and (d) show the corresponding final 3D configurations. (c and f) Normalized strain energy versus out-of-plane displacement for (t_SU8, t_SiNx, σ_residual, ε_release ) = (3 μm, 100 nm, 480 Mpa, 7.5%), (4 μm, 100 nm, 480 Mpa, 1.6%) and (4 μm, 100 nm, 480 Mpa, 2.4%), with the insets showing the stable buckling modes at the corresponding released strains. Here, h is the out-of-plane dimension of the first-floor structure, and it varies with changing the released strain. (g) Normalized strain energy versus out-of-plane displacement for (t_SiNx, σ_residual, ε_release) = (100 nm, 480 Mpa, 10%) and three different SU8 thicknesses. (h) Strain energy barrier versus released strain for (t_SiNx, σ_residual, ε_release) = (100 nm, 480 Mpa, 10%) and three different SU8 thicknesses. (i) Design diagram in the space of residual stress (σ_residual) and SU8 thickness (t_SU8), for t_SiNx = 50 nm, 100 nm and 150 nm. The geometric dimensions of the 2D precursor are the same as that in Figure 1, and the prestrain adopted in the analyses is 80%.

The design parameters (4 μm, 100 nm, 480 MPa) lead to a different characteristic variation in the strain energy, as shown in Figure 3d–f. Here, for ε_release = 0~2.4%, the pop-down mode corresponds to the only stable buckling mode, due to the single energy well in Figure 3f. As the ε_release increases beyond 2.4%, the pop-down mode transforms into the pop-up mode which corresponds to the single energy minimum in Figure 3f (i.e., with zero energy barrier, E_barrier = 0).

These observations indicate that the buckling mode is mainly governed by the existence of an energy barrier. External energy input can, however, overcome this barrier, leading to a transformation between the two different modes. The probability of transformation is directly related to the magnitude of the barrier, as confirmed in Figure 3g and h. Specifically, the non-zero energy barrier of point ‘2’ in Figure 2a is larger than that of point ‘10’, indicating a high probability to maintain the pop-down mode. The reverse energy barrier of point ‘2’ is lower than that of point ‘10’ (Figure 3g), indicating a high probability to switch back to pop-down mode if the structure is in the pop-up mode, consistent with the experimental results in Figure 2c. Meanwhile, because the energy barrier of point ‘11’ in Figure 2a is zero for ε_release in the range of 10% to 20%, the structure spontaneously transforms into the pop-up mode. Moreover, its reverse energy barrier is much larger than the other two points, leading to a lower probability to transform back, consistent with the experimental results in Figure 2c. Figure 3i presents an extended design diagram of Figure 2a that accounts for the influence of SiNx thickness. The results show that the magnitude of the residual stress required to achieve a pop-down mode decreases with increasing the SiNx thickness for ranges (e.g., from 0 to 400 nm) of interest here.

2.3 Complex hierarchical 3D mesostructures with deterministic buckling modes

With this model of the mechanics as a guide, a broad set of complex hierarchical 3D structures with different buckling modes can be assembled in a deterministic manner, with the aid of residual stresses. Figure 4 and Figure S8 (Supporting Information) present FEA predictions and experimental results for 10 complex mesostructures in SU8 (5 μm) that each incorporate stress-controlling layers of SiNx (100 nm), along with the designs of the corresponding 2D precursors. The top left frame of Figure 4a presents a precursor that includes four triangles with centroids each connected by three ribbons (denoted by group ➀➁➂➃) without any SiNx. The six small hexagons (red) adhere strongly to a biaxially prestrained elastomeric substrate. After relaxing the prestrain, the ribbons of groups ➀➁➂ pop up, while those of group ➃ pop down, corresponding to mode I. The addition of SiNx layers with compressive residual stress (σ_residual = −580 MPa, dark yellow) to local regions of the precursor switches the bending direction of the associated ribbons. For example, when SiNx layers are on all the ribbon groups (➀➁➂➃), then all of the relevant ribbons pop up, corresponding to mode II (Figure 4a, middle). With SiNx layers only on ribbons of group ➃, those ribbons pop up while the ribbons of other groups pop down (mode III, bottom row of Figure 4a). Figure 4b shows the design diagram for this set of 3D structures, in which the red dashed line indicates the minimum SU8 thickness for full delamination. The blue and pink lines are the boundaries between mode I and mode II and between mode I and mode III.

Figure 4.

3D mesostructures formed through the approach of compressive buckling assisted by residual stresses. (a) 2D precursors, FEA predictions and SEM images for triangular ribbon networks made of SiNx and polymer (SU8). (b) Design diagram of triangular ribbon networks in the space of residual stress (σ_residual) and SU8 thickness (t_SU8) for selection of different buckling modes. (c) 2D precursors, FEA predictions and optical images for triple-floor structures made of SiNx and bilayers of gold and polymer (SU8). (d) Design diagram of triple-floor structures in the space of residual stress (σ_residual) and SU8 thickness (t_SU8) for selection of different buckling modes. Scale bars, 500 μm.

Figure 4c shows a 3D mesostructure with a triple-floor architecture that corresponds to a 2D precursor without any SiNx (Figure 4c, left top).^[29] The material composition is almost identical to that of structures in Figure 4a, except for the addition of a layer of gold (30 nm) to enhance visibility under an optical microscope. The ribbons ➀➁ undergo an additional level of buckling to form an elevated “second floor”, while ribbon ➂ forms the third floor (Figure 4c, top). With the addition of SiNx layers (tensile residual stress, σ_residual = +480 Mpa, indigo), the third floor can either deform in an asymmetric manner (Figure 4c, middle) or pop down (Fig 4c, bottom). In addition to the locations of the SiNx layers, the sign of the residual stress also plays a crucial role. Figure S8 (Supporting Information) indicates that with the same 2D precursor and SiNx layers, tensile and compressive residual stresses yield distinct 3D configurations (the last two modes), both of which differ from the case without SiNx (the first mode). In all of the above examples, experimental results show excellent agreement with FEA predictions, establishing the computational models as reliable tools for rapid design optimization.

2.4 Application in a mechanically tunable micro-balance device

The ability to control 3D geometries, including the shapes of local regions, represents an attractive feature of the addition of stress-controlling layers. Figure 5a–e provides a simple device demonstration in the form of a tunable micro-balance for mass measurement. The design of the 2D precursor appears in Figure 5a. The part in indigo consists of a bilayer of SiNx (100 nm) and SU8 (5 μm), and the other part (blue and red) consists of a single-layer SU8 (10 μm). A tensile residual stress of 480 MPa in the SiNx layer ensures that the central part (indigo) pops down during assembly to facilitate the placement of microscale object to be measured. Fully releasing the prestrain in the substrate results in a 3D structure with a flat plate in the center (Figure 5b). A small mass (e.g., a few milligrams to tens of milligrams) is placed on the plate, deforming the structure downward by an amount that can be recorded by a nano-indenter (Figure S9, Supporting Information) or other metrology tool. The relationship between mass and displacement can be calibrated by experimental results and numerical simulations. Figure 5c illustrates a linear relationship between the displacement and mass. The upper limit of the measurement range corresponds to the mass needed to initiate physical contact between the plate and the substrate. FEA results in Figure 5d and e demonstrate that this limit can be adjusted by changing the prestrain, or equivalently, by stretching the underlying substrate after 3D assembly. This device can be useful for the microfluidic applications of 3D mesostructures such as MEMS-based mass measuring system for monitoring and separation of colloidal silica micro particles with the radius on the order of hundreds of microns.^[75,76]

Figure 5.

A simple, mechanically tunable micro-balance device. (a) 2D precursor for the device. (b) FEA prediction and SEM images from two different viewing angles. (c) Measured and computed dependence of the mass on the vertical displacement. (d) Mass versus vertical displacement for devices assembled with four different levels of prestrain, along with their corresponding 3D configurations. (e) The range of the micro-balance as a function of the prestrain. Scale bars, 1 mm.

2.5 Assembly of 3D structures with geometries previously inaccessible

The same residual-stress strategy can also enable formation of complex structures with 3D topologies that differ qualitatively from any of the buckling modes. Here, the utility of patterned shape memory polymers (SMP) as a means for introducing the stresses provide examples complementary to those achievable with SiNx. Specifically, as detailed in the Experimental Section, the SMP layers can involve large residual strains (~20%, corresponding to ~16 MPa residual stress at 100 °C), and thicknesses (> 60 μm), sufficient for forces that can govern the 3D transformation of targeted regions of a 2D precursor. To demonstrate the diversity of applicable material classes for this deterministic assembly strategy, a bilayer of Cu (thickness = 1 μm)/PET (thickness = 50 μm) (blue) was used for the formation of 3D structures.. Figure 6 presents FEA predictions and millimeter-scale experiments achieved with 2D precursors in a bilayer of Cu/PET (blue) with the addition SMP layers (thickness = 100 μm) at strategically designed regions. Here, the SMP layer can adhered to the precursor on the top (indigo) or the bottom (dark yellow). Detailed fabrication procedures are in the Experimental Section, and Figure S10 (Supporting Information).

Figure 6.

3D millimeter-scale structures formed through the use of shape memory polymers (SMP). (a) 2D precursors, FEA predictions and optical images for a complex 3D table structure made of SMP and bilayers of copper and PET. The structure here is formed in a way that compressive buckling and stress-induced bending work independently. The results in the top and bottom rows represent the 3D configuration before and after releasing the prestrain in SMP, respectively. (b) Similar results for a hierarchical 3D structure. (c,d) Similar results for two structures with multiple folds formed by coupled compressive buckling and stressed-induced bending. Scale bars, 5 mm.

Figure 6a presents a complex 3D table structure assembled through global buckling and local rolling of the 2D precursor. Here, the rolling follows from the mismatch strain between the SMP and other layers upon heating in water (100 °C), leading to formation of four circular rings on top of the buckled table (Figure 6a, right bottom). Unlike examples described previously, this hybrid 3D configuration does not correspond to any of the buckling modes of the 2D precursor without the SMP. Figure 6b corresponds to a hierarchical 3D structure in the form of three square membranes decorated symmetrically with twelve circular rings. This class of architectures with lifted circular rings could be further combined with semiconductor techniques to achieve optoelectronic applications, for example, as optical ring resonators that offer signal processing and communication at an enhanced efficiency^[77].

Coupled compressive buckling and stressed-induced bending are also possible with appropriate designs of 2D precursors. Two examples appear in Figure 6c and d, both of which adopt a straight ribbon design with non-uniform widths and leverage residual stresses in the SMP layer to control the folding direction at localized regions for multiple folds. In the first design (Figure 6c, left), the SMP layers exist at five narrow regions in the ribbon, with two on the top (indigo) and the other three on the bottom side (dark yellow). The ribbon pops up into an arc via global compressive buckling (Figure 6c, right top) after release of prestrain in the elastomeric substrate. This arc then reshapes into a wavy structure with five folds (Figure 6c, right bottom) after activating the SMP. The second design in Figure 6d has a 2D precursor similar to that of Figure 6c, except for the distribution of SMP layers (Figure 6c, left). The final 3D structure corresponds to a wavy pattern with three folds (Figure 6d, right bottom). In all cases, the 3D configurations predicted by FEA agree well with experimental results.

3. Conclusion

In summary, this work introduces residual stresses as a design strategy enhancement on to buckling-guided approaches for deterministic assembly of multi-level 3D mesostructures. Combined numerical simulations and experimental observations reveal the underlying physics and design considerations. With carefully configured residual-stress layers and judicious selection of layout parameters, complex buckling modes with previously inaccessible 3D topologies can be achieved. In one simple case, a 3D structure that incorporates a platform with a highly linear displacement-mass relationship provides a basic example in micro-balance based mass measurement, with a tunable range. In a complementary set of structures, residual stress not only controls the buckling mode, but imparts sufficient forces to create entirely differentiated 3D geometries. The materials systems presented here, i.e. SiNx and SMP, represent a small fraction of the possibilities that could be considered, such as environmentally responsive systems.

4. Experimental Section

4.1 Fabrication of micrometer-scale 3D structure with SiNx layer

Electron beam evaporation formed a bilayer of 5 nm of chromium and 100 nm of gold onto a clean silicon wafer at pressures between 0.7–3.4 μTorr, and at a rates of 0.5–0.7 and 0.9–1.2 Å/s, respectively. Following deposition, loading the wafer into a dual-frequency plasma enhanced chemical vapor deposition (PECVD) enabled deposition of 100 nm of silicon nitride (SiNx), either at high or low frequencies to generate films with tensile or compressive stresses, respectively. Specifically, tensile stress is generated by low density Si-N bonds stretching to interact with each other, which occurs primarily under high frequency deposition condition; compressive stress is generated under low-frequency and high-power condition which results in excess amine and other fragments. Details of film chemistry and strain generation can be found elsewhere.^[32,78] Photolithographically patterning AZ5214 photoresist and then etching away the exposed regions of the SiNx using CF₄ reactive ion etching, backstopped by the gold sacrificial layer. A barrel plasma etcher with O₂ gas at 500W for 3 min removed the photoresist.

Spin-coating yielded a thin layer of adhesion promoter (Omnicoat®, Microchem) and an overlayer of a photodefinable epoxy (SU8, Microchem). Photopatterning the SU8 defined the target geometries. After a brief exposure to oxygen plasma to remove the exposed adhesion promoter, dipping the wafer into gold etchant (Type TFA, Transene) partially undercut the gold. Photolithography with AZ5214 photoresist yielded a pattern to cover all regions of the SU8 except areas to define the bonding sites. Next, immersion in gold etching overnight completed removed the gold layer, to allow retrieval of the structures (i.e. 2D precursors) using a polydimethylsiloxane (PDMS) stamp via transfer printing. Before transfer, thin layers of titanium (5 nm) and silicon dioxide (40 nm) deposited onto the precursors by electron beam evaporator created surface chemistry for improved adhesion at the bonding sites. A water-soluble polyvinyl alcohol (PVA) tape enabled retrieval of the 2D precursors from the PDMS stamp, for subsequent lamination onto a UV-ozone treated, pre-stretched elastomer substrate (thickness = 0.4 mm, Dragon Skin®, Smooth-on). After curing in a convection oven at 70 °C for 7 min, immersion in warm water dissolved the PVA tape. Exposure to an acetone bath for 20 min led to full undercut of the AZ5214 layer. Finally, slowly releasing the prestrain led to formation of the 3D structures.

A schematic illustration of the procedure appears in Figure S2 (Supporting Information).

4.2 Fabrication of millimeter-scale 3D structure with SMP layer

An automated cutting machine formed structures in bilayers of copper (1 μm)/PET (50 μm). A commercial 3D printer (Stratasys Ltd.) served as a means to pattern the SMP in the form of two parallel ribbons (100 μm) connected to the cuboids at both ends (Figure S11, Supporting Information). Each layer formed in this way has a thickness of 16 μm, and each 2D ribbons consisted of 4 or more layers. The printed structure was then pre-stretched uniaxially in hot water (100 °C) for ~ 2 min by 20%. After cooling the structure to room temperature, parallel ribbons of SMP were cut to required dimensions. Adhering the SMP layer to the copper/PET layer on the top or bottom side by a commercial adhesive (Super Glue, Gorilla Glue Company) completed the preparation of the 2D precursors.

A thin silicone substrate (2 mm in thickness, Dragon Skin) served as the assembly platform. Super Glue dispensed at desired locations on the 2D precursors resulted in strong bonding to the silicone substrate, after curing for ~ 10 min at room temperature. Slowly releasing the prestrain in the substrate, with a strain rate of < 0.008 s⁻¹, completed the assembly process. Placing the entire structure into hot water (100 °C) released the prestrain in the SMP layer to reshape the 3D geometry defined by buckling.