Significance
Cell guidance phenotypes play essential functions in life processes, and their mechanisms generally rely on sophisticated biosignaling pathways, like in chemotaxis. In contrast, we reveal here a mechanotaxis phenotype of fish keratocytes orienting with or against the direction of flow that relies on a purely mechanical bias. The torque exerted by flow on the asymmetric shape of keratocytes takes opposite orientations depending on keratocyte shapes, and a simple mechanics model fully predicts the orientation of individual cells. This original passive mechanism implies a potential absence of alternative biosignaling mechanism and of physiological function. This elegant reductionist approach to a complex biological phenomenon also exemplifies how morphological diversity can lead to categorically distinct behaviors.
Keywords: directed migration, mechanotaxis, keratocytes, flow, mechanotransduction
Abstract
While cell migration can be directed by various mechanical cues such as force, deformation, stiffness, or flow, the associated mechanisms and functions may remain elusive. Single cell migration against flow, repeatedly reported with leukocytes, is arguably considered as active and mediated by integrin mechanotransduction, or passive and determined by a mechanical bias. Here, we reveal a phenotype of flow mechanotaxis with fish epithelial keratocytes that orient upstream or downstream at shear stresses around tens of dyn cm−2. We show that each cell has an intrinsic orientation that results from the mechanical interaction of flow with its morphology. The bulbous trailing edge of a keratocyte generates a hydrodynamical torque under flow that stabilizes an upstream orientation, just as the heavy lower edge of a roly-poly toy generates a gravitational torque that stabilizes an upright position. In turn, the wide and flat leading edge of keratocytes destabilizes upstream orientation, allowing the existence of two distinct phenotypes. To formalize these observations, we propose a simple mechanical model that considers keratocyte morphology as a hemisphere preceded by a wide thin sheet. Our findings show that this model can recapitulate the phase diagram of single cell orientation under flow without adjustable parameters. From a larger perspective, this passive mechanism of keratocytes flow mechanotaxis implies a potential absence of physiological function and evolution-driven process.
Directed cell migration is essential to most processes sustaining animal life such as development, feeding, immune defense, or reproduction. Cells can respond to various cues such as chemicals (chemotaxis, haptotaxis) (1, 2), electric fields (galvanotaxis)(3), magnetic fields (magnetotaxis) (4), or mechanical stimuli (durotaxis, topotaxis, barotaxis, flowtaxis) (5–11), which supports that evolution shaped sophisticated mechanisms, allowing cells to adapt to their environment and optimize their benefits (1). Indeed, chemotaxis is knowingly associated to numerous physiological functions, and the underlying machinery relies on G-protein chemosensors that trigger internal signaling cascades and eventually reorganize the cytoskeleton (12). In comparison, mechanotaxis encompasses a wide family of guidance processes that were revealed more recently, and there is currently an important effort to identify the associated functions and mechanisms (1, 13).
We consider here the case of mechanotaxis by flow, and more specifically the peculiar case of single cells that migrate against flow. Downstream phenotypes of single cells were observed with mesenchymal cells such as endothelial cells (14) and in ameboid cells such as ameba (15) and leukocytes (16). However, upstream phenotypes of single cells were only reported with one mesenchymal cancer cell model in 3D (10, 17) and with ameboid leukocytes in 2D (6, 18–26). While migration in the direction of flow might be attributed to passive drifting, migration against flow suggests strongly that flow must trigger signaling events, allowing cells to react and orient against the drifting direction. All studies agree that integrin signaling is a key player for upstream mechanotaxis (6, 10, 17, 19–28) and some biosignaling pathways were found to be associated to upstream phenotypes (7, 10, 26), which is consistent with the hypothesis that a sophisticated biosignaling controls upstream mechanism. At the same time, some upstream phenotypes were fully explained by passive biomechanical biases (19, 27, 28) without a need of mechanotransduction by flow. Fundamental questions about the exact mechanism and functions of upstream mechanotaxis remain therefore arguable. Specifically, is upstream mechanotaxis a passive or active phenomenon, what is the exact role of integrins, and is 2D upstream phenotype restricted to ameboid cells?
Here, we report a phenotype of upstream mechanotaxis with fish epithelial keratocytes, a well-established migration model of nonameboid cells (29, 30). We show that cell orientation can be explained by a passive mechanical bias, the morphology of each individual cell determining the orientation of the torque exerted by flow, and consequently the stability of the upstream orientation.
Results
Keratocytes Orient Mainly Downstream Under Flow.
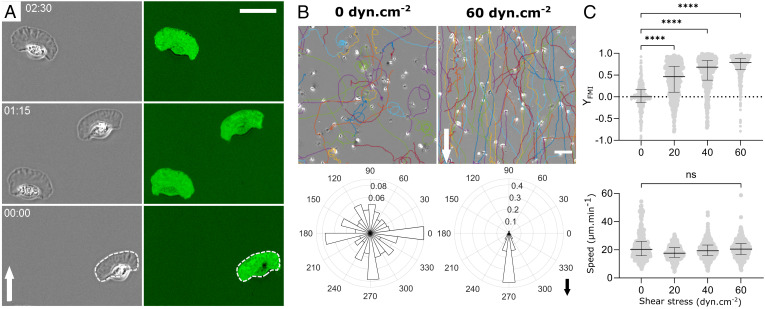
Fish epidermal keratocytes on glass substrates were highly polarized and migrated persistently at high speed by adopting a typical fan-shaped morphology composed of a thin widespread lamellipod at the front and a bulbous cell body at the rear (Fig. 1A and Movie S1). Interference microscopy also showed that cells were generally adherent in the whole projected area (Fig. 1A and Movie S1). Our findings showed that average cell speed under flow remained unaffected around 20 µm/min for shear stresses as high as 60 dyn cm−2, whereas the average cell orientation was markedly influenced by flow and characterized by a net downstream bias (Fig. 1 B and C). The average forward migration index, YFMI, i.e., the ratio between the algebraic endpoint displacement along the direction of flow and the length of the curvilinear trajectory during a given period of time (here 40 min), increased linearly with shear stress from 0 without flow to 0.85 for a shear stress of σ = 60 dyn cm−2 (Fig. 1C).
Fig. 1.
Keratocytes orient mainly downstream under flow. (A) Image sequences in phase-contrast mode (Left) and reflection interference contrast microscopy (RICM) mode (Right) of keratocytes crawling on glass. The contrast was inverted in RICM images and bright green corresponds to the adhesion fingerprint. The white dashed line underlines the apparent contour of cells in phase-contrast images. Time min:s. (Scale bar, 30 µm.) (Movie S1) (B) Cell trajectories in a representative experiment (Top) and rose plots showing the angular distribution of the trajectories taking into account the first and last points of each trajectory (Bottom) without flow (Left) and with a shear stress of 60 dyn cm−2 (Right). (Scale bar, 100 µm.) Three and seven independent experiments without and with flow, respectively, and 250 frames per cell with time interval 10 s, >200 cells per experiment. Arrows indicate flow direction. (C) Forward migration index YFMI (Top) and speed (Bottom) versus shear stress. Each data point corresponds to one cell tracked by 250 images taken every 10 s. Bars are median ± interquartile range. Kruskal–Wallis test, one-way ANOVA for non-Gaussian distribution, ****P < 0.0001. Two independent experiments, N > 400 cells per condition.
A Subpopulation of Keratocytes Has Intrinsic Upstream Phenotype.
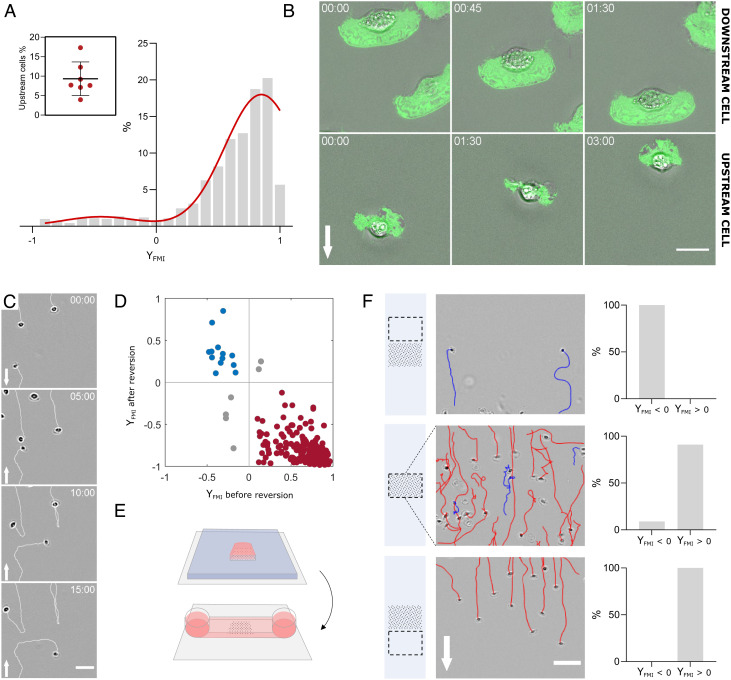
While most cells oriented with the flow and the average forward migration index YFMI was markedly positive, the distribution of single-cell YFMI was bimodal, with a small population (~10%) of cells that oriented against the flow (Fig. 2A and Movie S2). The upstream-bound cells had a similar speed as downstream-bound cells, while they had seemingly a smaller size (Fig. 2B and Movie S2), as discussed thereafter. Importantly, when flow direction was reversed by 180°, each given cell performed a U-turn (Fig. 2 C and D and Movie S3), demonstrating that upstream or downstream phenotype is an intrinsic property of each individual cell. To further test this assertion, we have undertaken to sort cells functionally according to their phenotype under flow. To this aim, we used removable silicon stencils to seed cells selectively on a stripe perpendicular to the direction of flow (Fig. 2E), and stencils were removed right before the application of flow. Under flow, the zone downstream of the seeding stripe selected 100% of cells with downstream phenotype, whereas the zone upstream of the seeding stripe selected 100% of cells with upstream phenotype (Fig. 2F and Movie S4). Altogether, these findings show that keratocytes are equipped with a set of biochemical and/or biophysical properties that determine their fate under flow. While small cells seem more prone to orient upstream, the exact properties that mediate orientation under flow remain to be determined.
Fig. 2.
A subpopulation of keratocytes displays intrinsic upstream phenotype. (A) Histogram of forward migration index YFMI for individual cells is bimodal with a downstream-bound (90.7% of cells) population and an upstream-bound (9.3% of cells) population. Red line is a fit by a double Gaussian. Shear stress 60 dyn cm−2. Seven independent experiments, >200 cells per experiments, and 250 frames with time interval 10 s for each cell; values of each boxplot correspond to the average of all experiments. (Movie S2). Inset- Fraction of upstream-bound cells in each of the seven experiments. (B) Superposition of phase-contrast (gray) and inverted RICM (green) images of representative downstream-bound (Top) and upstream-bound (Bottom) cells. White arrows indicate flow direction. Shear stress 60 dyn cm−2. Time min:s. (Scale bar, 15 µm.) (Movies S1 and S7). (C) Image sequence showing downstream-bound and upstream-bound cells making U-turns after flow reversal at time t = 5 min. Arrow indicates flow direction. Shear stress is 60 dyn cm−2. (Scale bar, 50 µm, time min:s.) (Movie S3). (D) 2D plot of forward migration indexes YFMI for individual cells before and after flow reversal (red for downstream, blue for upstream) under a shear stress of 60 dyn cm−2. Data from two independent experiments, >100 cells per experiments, 300 frames per cell with time interval 20 s, and flow reversal at the 150th frame. Spearman’s correlation: rSpearman = −0.6. (E) Cartoon illustrating the cell seeding process in a stripe. A PDMS stencil (blue) with a 5 × 5 mm opening is used to seed cells in a selective zone of a coverslip (gray) (Top). After seeding, the stencil is replaced by an IBIDI channel (Bottom). Pink corresponds to medium and black dotted area to the cell seeding zone. (F) Functional cell sorting by flow mechanotaxis. (Left) Cartoon illustrating the imaging zone (dashed rectangle) relative to the initial seeding zone (black dotted area). (Middle) Images and tracks from a representative experiment (red for downstream, blue for upstream) of cells above, inside, and the below the seeding zone at 60 dyn cm−2. Arrows indicate flow direction. (Scale bar, 100 µm.) (Right) Percentage of cells with up- or down-stream orientation above, inside, and below the seeding zone. Data from three independent experiments, >200 cells per experiments. (Movie S4).
Prominent Cell Rear Is Required for Upstream Orientation.
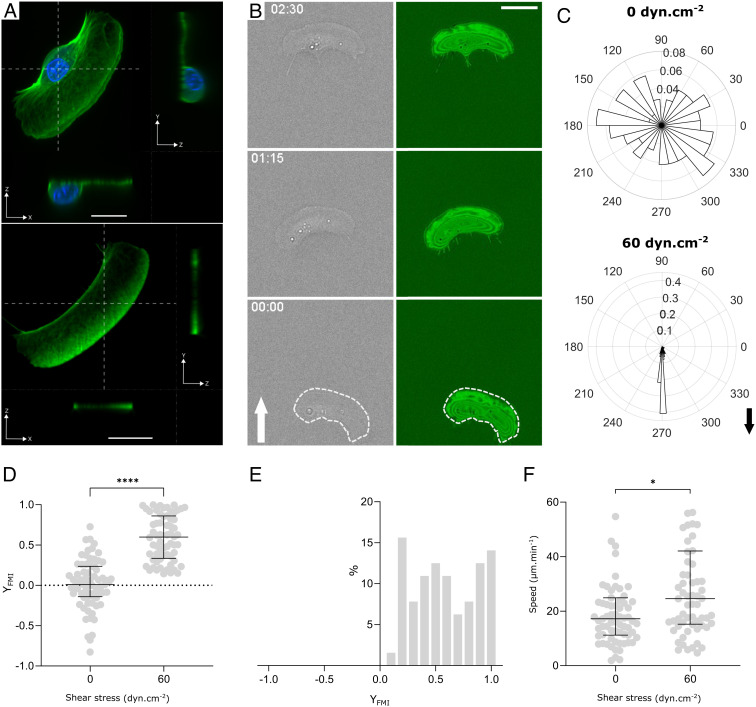
Upstream migration of lymphocytes was proposed to rely on a protruding cell rear, the uropod, that acted as a windvane (28). Since keratocytes are also characterized by a bulbous cell rear (Fig. 3 A, Top), it was tempting to question what role the cell rear body may play in the upstream phenotype of keratocytes. We first attempted a perturbative approach by removing the keratocytes rear body using staurosporin, a drug known to provoke the fragmentation of keratocytes (31). As reported previously, the resulting fragments of lamellipods resemble keratocytes without the bulbous rear (31) (Fig. 3 A, Bottom). In the absence of flow, fragments migrated with a random orientation and an average speed of around 20 µm/min that is close to the characteristics of keratocytes (Fig. 3F and Movie S5). These findings are in line with the idea that cell rear body is but a passive cargo, and the lamellipod is a mechanically autonomous engine (29). In the presence of flow, the average orientation was strongly biased in the direction of flow (Fig. 3 B–D and Movie S5), and the subpopulation of migrators with an upstream phenotype that was systematically observed with keratocytes was totally absent with fragments of keratocytes (Fig. 3E). These results indicate that the bulbous rear body of keratocytes is required for upstream migration and suggest that it may be directly responsible for upstream orientation.
Fig. 3.
Trailing edge is required for upstream phenotype. (A) Confocal images of a whole keratocyte (Top) and of a fragment of keratocyte lamellipod (Bottom) with immunostaining of membrane (green) and nucleus (blue). x–y images correspond to projected images, while x–z and y–z images correspond to cross-sections at planes indicated by white dashed lines. (Scale bar, 10 µm.) (B) Sequences of phase-contrast (gray) and inverted RICM (green) images of a fragment crawling on glass. The white arrow indicates the flow direction. The white dashed line underlines the apparent contour of cells in phase-contrast images. Shear stress is 60 dyn cm−2. Time min:s. (Scale bar, 10 µm.) (Movie S5). (C) Angle histogram showing the distribution of fragment orientation with and without shear stress of 60 dyn cm−2. The length of each bin of the rose plots reflects the fraction of cells with a given angle. Black arrow indicates the flow direction. (D) Forward migration index YFMI versus shear stress. Each data point corresponds to one fragment tracked by 250 images taken every 10 s. Data from two independent experiments, >30 fragments per experiment. Bars are median ± interquartile range. Student’s t test, ****P < 0.0001. (E) Histogram of YFMI for individual fragments displays a downstream-bound population. Shear stress is 60 dyn cm−2. Data from two independent experiments, >30 fragments per experiment, 250 frames taken every 10 s. (F) Speed versus shear stress. Data from two independent experiments, >30 fragments per experiment. Bars are median ± interquartile range. Welsh’s t test, *P = 0.0351.
Lamellipods Foster Downstream Orientation.
Previous results with neutrophils and lymphocytes support that a lamellipod loosely connected to a substrate, either on its main projected area or at its extreme front edge, is passively funneled by flow and induces a preferential downstream orientation of the whole cell (19, 27, 32, 33). The fact that the lamellipod of keratocytes tend to orient downstream was strongly suggested by experiments of flow reversal: upon change of flow direction, downstream-bound cells were suddenly facing flow and their lamellipods were often pushed upside down (Movie S6). Additionally, the fact that fragments orient with flow supports further that the lamellipodial engine of keratocytes fosters downstream orientation of the whole cell. Altogether, keratocytes under flow are submitted to conflictual mechanical effects, with flow on cell rear and on cell front fostering upstream and downstream migration, respectively.
Fluctuations of Leading Edge Adhesion Do Not Perturb Upstream Migration.
Besides cell shape, cell adhesion along the axis of polarization was also shown to be determinant for the orientation of lymphocytes under flow, with either upstream or downstream phenotype observed when either the trailing or the leading edge of cells was detached, respectively. Here, keratocytes had their whole projected area globally adherent in the absence of flow (Fig. 2 B, Top), which strongly differs from the sharp asymmetry of adhesion observed on leukocytes. This suggests that polarization of adhesion may not play a key role in the orientation under flow of keratocytes. However, for upstream-bounded cells, lamellipods were repeatedly detached by flow at their frontal edge, before eventually resuming their growth against flow and readhering (Fig. 2 B, Bottom and Movie S7). These frontal detachments did not seem to trigger a collapse of migration nor of upstream orientation, which sounds a priori inconsistent with the idea that a detached lamellipod fosters downstream migration.
The Stability of Cell Orientations Is Modeled with Cell Morphology and a Mechanical Bias.
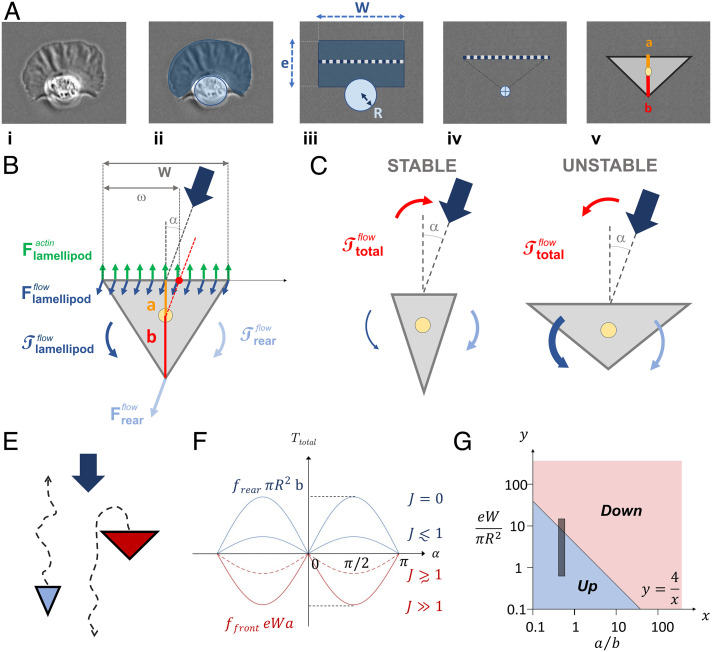
The antagonistic effects of cell front and cell rear on the orientation of keratocytes under flow can be considered more quantitatively within a reductionist mechanical model. A keratocyte (Fig. 4 A, i) is essentially composed of a thin lamellipod at the front, that we simplify into a rectangle sheet of width W and extension e, and a bulbous cell body in rear that we simplify into a hemisphere of radius R (Fig. 4 A, ii). The sizes W and e of the lamellipod and the radius R of the bulbous body allow one to determine the intensity of the force exerted by flow on the leading and trailing edges, respectively. To determine the torque exerted by flow on the cell, i.e., the capability of the forces to produce a change in the rotational motion of the cell, we then considered the resultant of the forces acting on the median of the rectangle sheet in cell front, and on the center of mass of the hemisphere in cell rear (Fig. 4 A, iii). From a mechanical perspective, the median of the lamellipod and the center of the bulbous rear reduce the mechanical geometry of a keratocyte into a triangle (Fig. 4 A, iv). For the calculation of the torques exerted by flow, the distances between the axis of forces acting on the cell and the axis of cell rotation depend on the width of the leading edge of the triangle cell, W, and the two lengths, a and b, separating the center of rotation of the cell from the frontal edge and the rear vertex of the triangle cell, respectively (Fig. 4 A, v).
Fig. 4.
A mechanical model explains the versatile orientation of keratocytes under flow by the orientation of torque exerted by flow on the asymmetric cell morphologies. (A) Rationale for a triangle cell model. i) A keratocyte is composed of ii) a flat lamellipod in front (dark blue) and a protruding cell rear (light blue). iii) To calculate flow interactions on cell body, we consider the lamellipod as a thin rectangle of dimensions e and W (dark blue) and the cell rear body as a hemisphere of radius R (light blue). In a solid mechanic approach, we reduce the action of flow to its action on the median of the rectangular leading edge (dashed line) and the center of mass of the circular trailing edge (crossed dot). iv) This frontal median and the rear vertex define a minimal triangle keratocyte. v) The distance between the frontal edge and the rear vertex of the triangle cell with the center of rotation of the triangle cell (yellow dot) is called a and b, respectively. (B) Schematics of forces and torques exerted on a triangle keratocyte facing flow at a finite angle α. The internal forces of actin polymerization (green arrow) push cell forward, while flow pushes the frontal edge (dark blue) and rear vertex (light blue) downstream. (C) Schematics of cells with geometric features fostering either stable or unstable upstream phenotype. (D) Schematics illustrating the phase separation into upstream and downstream phenotypes depending on cell morphologies. (E) Total torque versus angle α for different morphologies (J values) according to Eq. 5. (F) Phase diagram of upstream (blue) and downstream (red) phenotypes depending on cell morphological parameters and according to Eq. 5 and considering a value (34, 35). The gray zone delineates the domain of morphologies observed for keratocytes in our experiments.
Let us then consider that a triangle cell faces flow at an angle α (Fig. 4B). The forces acting on it comprises an internal component exerted by polymerizing actin, that propulses the cell front forward, and the two external components exerted by flow on cell front, and on cell rear, . The force of actin in the lamellipod pushes the frontal edge of the triangle cell forward in the direction of cell polarity (Fig. 4B). The torque on the cell associated to this force, is therefore always null.
| [1] |
The force of flow on the bulbous cell body exerts on the cell a torque, that can be written as:
| [2] |
where is the prefactor of the hydrodynamic drag per unit of the projected area for a hemisphere protruding from a plane in a laminar flow (34, 35), is the viscosity of the medium, and is the shear rate. The torque exerted by the flow on the trailing edge, , is therefore always positive and tends to stabilize cell orientation against flow. This is reminiscent of roly-poly toys, for which the torque exerted by gravity on the heavy bottom edge stabilizes an orientation against gravity. Then, the torque of flow on cell front, , results from the force of flow integrated along the leading edge of the triangle cell. This torque is composed of a counterclockwise part on the downstream side (leeward) of the leading edge that tends to destabilize upstream orientation, and a clockwise part on the upstream side (windward) of the leading edge that tends to stabilize upstream orientation (Fig. 4B):
| [3] |
ω = W/2 + a tan(α) is the width of cell front on the downstream (leeward) side of the leading edge (Fig. 4B). The resultant can be reduced to:
| [4] |
where is the prefactor of the hydrodynamic drag per unit area on one side of a planar sheet in a laminar flow, is the viscosity of the medium, and is the shear rate. The torque on cell front is, therefore, always negative and tends to destabilize upstream migration. This is consistent with the observation that fragments of keratocytes, which are deprived of bulbous cell rear and are submitted to only, displayed downstream orientation only (Fig. 3E). Altogether, the total torque, on a triangle cell can be expressed as:
| [5] |
where
Interestingly, a critical parameter appears in Eq. 5 that determines the sign of the effective torque, , exerted by flow on a cell, and therefore the stability of cell orientation either upstream or downstream. Cells with migrate stably upstream, whereas cells with migrate stably downstream (Fig. 4 C and D). The factor is nondimensional and comprises three nondimensional ratios. The ratio of the hydrodynamic prefactors linking drag with cell topology (flat in front, hemispherical in rear) is identical for all cells and equal to around (34, 35). The ratio of the cellular extensions along the polarization differs from one cell to the other, and the smaller the ratio , the more stable the upstream orientation. Finally, the ratio of the projected area of the trailing edge and leading edge differs also from one cell to the other, and the smaller the ratio , the more stable the upstream orientation.
The fact that the model determines the orientation of a given cell only by intrinsic morphological parameters (i.e., ) is consistent with the observation that each cell has an intrinsic phenotype, either upstream or downstream. Besides, Eq. 5 says that the total torque depends on the angle α as a sine function for all cells, and on the J value of each individual cell linearly. The extremal torque values are limited by the extremal values J = 0 and J ≫ 1 that correspond to torque intensities of for upstream phenotype and eWa for downstream phenotype (Fig. 4E). These extreme values are not reached in practice because J values are limited by effective morphology parameters of real keratocytes. Interestingly, Eq. 5 allows one to establish a phase diagram of single cell orientation versus the cell morphological parameters and , with the phase boundary between upstream and downstream phases corresponding to , i.e., to the hyperbole (Fig. 4F). To position the domain of real keratocytes in the phase diagram, we used the range of cell morphological parameters observed experimentally, i.e., , and . Considering also that the projected area of keratocytes was globally adherent, we assume that the center of mass of the adhesive fingerprint is close to the center of rotation of the adherent keratocyte, so that the ratio can then be considered close to , which is the geometric value for the center of mass of a triangle. The domain of keratocytes in the phase diagram of Fig. 4F sits then exactly across the phase boundary. This result is remarkably consistent with the existence of both upstream and downstream phenotypes for keratocytes, and since there is no adjustable parameter in the model, the prediction that the shape distribution of keratocytes yields a double phenotype is absolute.
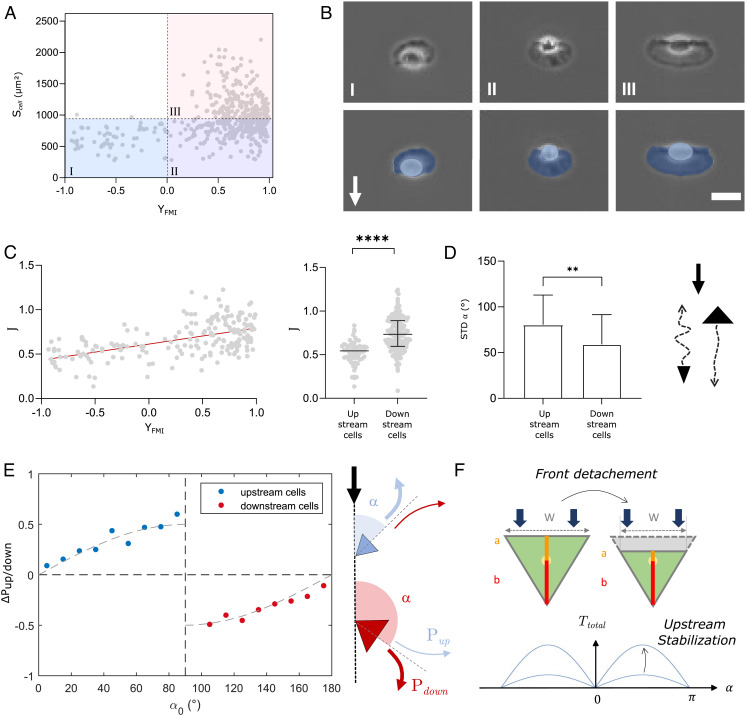
In the above, we considered the extreme limits of phenotypes, but Eq. 5 also yields predictions at the single cell level. Cell orientation is expected to correlate with the factor for each individual cell. Hence, while experiments showed that upstream-bound cells where always small, cell size is not the control parameter according to the model. This is consistent with the fact that the correlation between orientation and cells area is rather poor, with a Pearson coefficient rPearson = 0.31 (Fig. 5A). Hence, while it is true that upstream-bound cells are always small (the upper left quadrant above quadrant I is empty), downstream phenotype concerns both large (quadrant III) and small (quadrant II) cells. The representative images of cells in each quadrant of Fig. 5A are then reported in Fig. 5B. They suggest that downstream-bound cells (quadrants II and III) have larger leading edges than trailing edges, which qualitatively supports that the relative size of cell organelles is more relevant than the global cell size to determine cell orientation under flow. We, therefore, tested more quantitatively the correlation between the cell orientation YFMI and the parameter . For this, we consider that the component corresponds to the projected area of cell rear body, , and to the surface of the whole cell minus the surface of cell rear, . Then, taking the measured values and for each given cell, assuming a value in line with the triangle cell model, and taking the value imposed by hydrodynamic laws, we could dress the 2D plot of versus YFMI for individual cells (Fig. 5C). The correlation is significantly improved as compared to Fig. 5A, and the Pearson’s coefficient is now rPearson= 0.54. Furthermore, the transition between upstream and downstream phenotypes is found here at , which is remarkably close to the theoretical value of 1 considering the absence of adjustable parameters and the approximation of the triangle cell model. This result further underlines the capacity of the model to provide an accurate and almost absolute prediction of the upstream and downstream phenotypes at individual cell level.
Fig. 5.
Keratocyte morphology controls orientation under flow consistently with the model of torque on a triangle cell. (A) 2D plot of cell orientation under flow YFMI (at 60 dyn cm−2) and cell surface area . Linear regression yields rPearson=0.31. Two independent experiments, >200 cells per experiments, 250 frames with time interval 10 s for each cell. (B) Representative images of cells in quadrants I, II, and III of 2D plot in A (Top) and with Lamellipods colored in dark blue and cell body in light blue (Bottom). White arrow shows flow direction. (Scale bar, 20 µm.) (C) Correlation between single cell orientation and morphology. (Left) 2D plot of forward migration index YFMI (at 60 dyn cm−2) and control parameter . Linear regression (red line) yields rPearson= 0.54. (Right) Control parameter for upstream- and downstream-bound cells in two independent experiment, N > 100 cells per experiment, 250 frames with time interval 10 s for each cell. Unpaired t test, ****P < 0.001. (D) Effect of torque intensity on guidance strength. (Left) Standard deviation of cell orientation for upstream- and downstream-bound cells. Unpaired t test, P = 0.0035. (Right) Cartoons of cells with upstream or downstream orientation: the arrows illustrate tracks with fluctuations of direction. (E) Effect of torque intensity on instant guidance. (Left) Preferential probability to turn upstream, ΔPup/down = 2Pup−1, versus the angle between cell and flow directions α, for (blue) upstream- and (red) downstream-bound cells. 337 cells, 250 frames with time interval 10 s for each cell. The lines are sine functions. (Right) Cartoons of cells with upstream or downstream orientation and arrows representing instant probabilities to turn upstream, Pup, or downstream, Pdown. (F) Effect of lamellipod detachment on a triangle cell facing flow (green indicates adherent footprint). Reduction of a and W (Top) stabilizes upstream phenotype (Bottom) according to Eq. 5.
Let us then consider in the model that cell orientation has some stochasticity, which is needed to account for the random orientation of cells in the absence of flow. Assuming that the average orientation of cells under flow is proportional to the torque (which is reasonable for low torque), the mechanical model predicts that cell orientation under flow should be proportional to flow intensity or shear rate:
| [6] |
This linear dependence is reasonably consistent with experimental data (Fig. 1C). Experiments then yield that the standard deviation of cell orientation is higher for upstream-bound cells than for downstream-bound cells (Fig. 5D), which means that cell orientation is on average less stable for upstream than for downstream phenotypes. In the frame of the mechanical model, the intensity of the total torque is null when J = 1, i.e., when the torques on cell front and cell rear compensate each other, and it increases linearly with 1 − J, i.e., when the torques on cell front and cell rear are more asymmetric. The results of Fig. 5D suggest therefore that the total torque is on average weaker for upstream-bound cells than for downstream-bound cells, and consequently that upstream-bound cells are on average closer to the transition conditions than downstream-bound cells. This implies that the distribution of cell morphologies corresponds mostly to downstream phenotypes and that only a small wing of this distribution corresponds to cells across the transition boundary of the phase diagram. This deduction is indeed consistent with the experimental distribution of phenotypes in Fig. 2A. Hence, the model allows one to link the relative rarity of upstream-bound cells and the moderate stability of their orientation.
Let us now assume that the instant probability for a cell to reorient under flow increases linearly with the torque (which is reasonable for low torque). The preferential probability to turn upstream rather than downstream for a cell facing flow with an angle , , is then expected to be proportional to (Eq. 5 and Fig. 4E):
| [7] |
From experimental data, we considered all events where a cell direction faced the flow at an angle and compared cell orientation between two consecutive time points of 10 s. The probability to orient against flow, , was then determined as the ratio between the number of events where cells turned upstream versus the total number of events. The preferential probability to turn upstream for each angle was then calculated as (Fig. 5E). For upstream migrating cells, we find that tends to zero for , which is expected by symmetry, and increases with to a maximum positive value at , when the torque is maximal versus . Similarly, for downstream migrating cells, tends to zero for , which is expected by symmetry, and decreases with to a minimum negative value at , when the torque is maximal versus . Furthermore, Fig. 5E also shows that experimental follows reasonably a sine function versus as expected from Eq. 7.
Finally, experiments showed that the frontal edge of lamellipods repeatedly detached for upstream-bound cells without significantly perturbing cell orientation (Fig. 2B and Movie S7). This seems at first inconsistent with the idea that detachments of lamellipod foster downstream orientation, as observed with fragments of keratocytes here and with other cell types in the literature (19, 27, 32, 33). However, cell detachments of lamellipod also induce a decrease of lengths and (Fig. 5F) which, in the frame of the mechanical model, increases the relative effect of cell rear and therefore stabilizes upstream phenotype. In the end, the model predicts that upstream-bound cells maintain their orientation against flow with the help of lamellipod detachments, and not despite them.
Discussion
We have used in vitro microfluidic experiments to correlate quantitatively the functional state of keratocytes flow mechanotaxis from a large number of observations of cell morphology, speed, and orientation in various shear conditions. These data provided the basis to propose that orientation with or against flow is set by the morphology of cells that determines the orientation of the torque exerted by flow on cells. Although conceptually straightforward, our model allowed us to dress a phase diagram of orientation versus single-cell morphology that is consistent with experimental observations without adjustable parameters. This is the quantitative and absolute model linking a mechanotaxis mechanism to cell morphology. Overall, the picture is very simple: the upstream phenotype of keratocytes is stabilized by a prominent trailing edge that orients keratocytes against flow, in a similar way as the upstanding position of a roly-poly toy is stabilized by a heavy bottom edge that orients the roly-poly toy against gravity. This simple paradigm relating cell morphology and guidance is somehow reminiscent of the study by Keren et al. (30) that related cell morphology and speed (36), in which no regulatory elements such as microtubules, morphogenes, or signaling molecules was incorporated. The case of guidance here is even simpler as we do not need to consider molecular mechanism, when Keren et al.’s model was based on the dynamics of actin treadmilling and an inextensive membrane bag. In turn, one has to underline that our model relies on some strong approximations, as it overlooks the exact shapes and dynamical deformations of cell body, the fact that cells are not solid bodies, and the modulations of adhesion strength and traction forces in the contact zone. The model can therefore not explain the orientation of keratocytes in all details, but the fact that it recapitulates the main equilibrium and dynamical properties of keratocytes’ versatile orientation under flow without adjustable parameters strongly suggests that the main ingredients of the mechanism are captured. In this view, cells use no specific internal signaling to choose orientation under flow, they just move forward with some persistence, and flow biases passively their motion in a direction set by solid mechanics.
Upstream orientation had only been observed with cancer cells and leukocytes yet, and previous observations concerned 3D migration for cancer cells and 2D migration for leukocytes. The latter case of leukocytes is therefore more relevant to the present study. Leukocyte upstream migration was first suggested in vivo with a partial orientation against flow (42% of cells) for T lymphocytes on blood–brain barrier endothelial cells of mice with autoimmune lesions (37), and then confirmed in vitro with up to 90% of T lymphocytes facing flow at shear stress of 40 dyn.cm−2 on substrates coated by ligands of specialized adhesion molecules called integrins (6, 18). Upstream phenotype has attracted a special interest because it intuitively suggests the existence of an adaptive cellular mechanism to oppose flow, and other types of leukocytes were then found to orient against flow, such as B lymphocytes, neutrophils, and hematopoietic stem and progenitor cells (8–18). Interestingly, upstream phenotype of leukocytes was systematically linked to adhesion mediated by integrins Lymphocyte Function-associated Antigen-1 (LFA-1), whereas downstream phenotype seemed fostered by other integrins such as Very Late Antigen-4 (VLA-4) (6, 18–26). Furthermore, several signaling mechanisms involving LFA-1 were shown to be linked to flow orientation of leukocytes, including a crosstalk between integrins LFA-1 and VLA-4 (27), a differential polarization of LFA-1 and VLA-4 activation (19, 27), or the engagement of LFA-1 that activates phosphoinositide 3-kinase and ERK pathways (7, 26). Similarly, for cancer cells, upstream migration was associated with stress-induced activation of β1-integrins, and triggering of actin-mediated protrusions relies on associated focal adhesion proteins (vinculin, FAK, and paxillin). Altogether, these findings advocate the existence of active signaling mechanisms sustaining upstream migration and linking specific molecular mechanosensors (notably integrins) to cytoskeleton reorganization. However, the causality between the observed signaling events and cell orientation is not fully established, and a complete signaling mechanism has not been deciphered yet. Besides, Artemenko et al. (38) showed with leukocytes (and ameba Dictyostelium) that shear flow induced signal transduction events typically implied in chemotaxis, suggesting a universal interaction and/or integration between chemo- and mechano-taxis. However, direct evidence between mechanical guidance and chemotaxis pathways was not tested in their study. Then, beyond integrins and flow mechanotaxis, mechanobiology has identified important effectors in mechanotransduction cascades (e.g., YAP/TAZ(39, 40), PIEZO1 (41), and orai1 (42)), and several intracellular signaling pathways (e.g., WNT, TGFβ-family signals, FGF, and Notch) are knowingly mechanosensitive. However, it is not always clear when these mechanosensitive mechanisms are functionally important. In the end, the field of flow mechanotaxis remains largely uncharted and its potential associated biosignaling mechanisms are not fully unraveled.
In this context, our results with keratocytes show that upstream mechanotaxis is limited not to leukocytes or cancer cells, nor to a single specific integrin type, which further enlarges the domain of uncharted areas. For keratocytes, it has been previously reported that the mechanical asymmetries responsible for the turning behavior predominate at the rear of the cell (43). Interestingly, this is quite reminiscent of the observation that leukocytes’ turning behavior can be fully controlled by a mechanical action on their rear (28). Besides, internal feedback loops connecting myosin II contractility, adhesion strength, and actin network flow were found sufficient to explain keratocyte trajectories (43). Similarly, the internal feedback loops maintaining leukocytes’ front–rear polarization were essential to explain their directivity and orientation versus flow (19, 28). In addition, flow mechanotaxis of keratocytes in this work and of leukocytes in previous work can be explained by a passive mechanical bias, i.e., without mechanotransduction (19, 27, 28). Altogether, the mechanisms for upstream mechanotaxis of keratocytes and leukocytes are conceptually similar. Only the origin of the mechanical bias differs between the two systems: an imbalance of morphology between the leading and trailing edges for keratocytes and an imbalance of adhesion between the leading and trailing edges for leukocytes. An asset of passive mechanisms is to fully explain guidance with simple calculations of mechanics, whereas the validation of active mechanisms requires the deciphering of complex biosignaling pathways, which is a tenuous task that has not been achieved for flow mechanotaxis yet. Another general asset of passive mechanical mechanisms is their independence from a biological machinery, which allows similar phenotypes to occur with very different cell types.
Dealing with living cells, it is interesting to question the function of the phenotypes of interest. Mechanotaxis of ameba and leukocytes occurs at shear stresses of 4–20 dyn.cm−2 that correspond to physiological conditions. This let the possibility that the phenotypes may be effective in vivo, that they have a function, and that evolution may have shaped mechanisms to fulfill these functions. In turn, keratocytes display flow mechanotaxis at shear stresses of 20–60 dyn cm−2 that they do not experience when they are protected by fish scales. They may experience some significant stresses after a wound that exposes them to external flows. But considering that fishes swim at speeds about 10 cm/s, and simplifying a fish to a flat sheet in a flow, the Prandtl theory and Blasius equation (44) yield a shear stress of merely ~0.5 dyn cm−2 at 5 cm from the edge of the plate, which corresponds to the middle of the fish. This estimate, in agreement with literature data (45), suggests that keratocytes perform flow mechanotaxis for shear conditions that they do not encounter physiologically. A physiological function is then dubious, and evolution had a priori no opportunity to shape a specific biosignaling mechanism for keratocyte flow mechanotaxis. These remarks are consistent with a passive mechanical bias being mainly responsible for keratocyte flow mechanotaxis.
Finally, the versatile orientation of keratocytes under flow is quantitatively explained without adjustable parameters by a simple mechanical model. The identification of a functional passive mechanism does not exclude the existence of alternative mechanisms based on mechanotransduction, but it implies that such mechanisms do not necessarily exist.
Materials and Methods
Cell Culture.
For each experiment, three fish scales were taken off from Central American cichlids Hypsophrys Nicaraguensis and squeezed between two microscope glass slides with 200 µL of a mixture at a volume ratio 0.3/1 of deionized water and Leibovitz's L-15 medium (Gibco, Thermo Fisher Scientific) supplemented with 10% fetal calf serum (Gibco, Thermo Fisher Scientific), 1% penicillin–streptomycin (Gibco, Thermo Fisher Scientific), and 1.5 mM HEPES (Gibco, Thermo Fisher Scientific). After 20 h of incubation at 28°C, 1.5 mL of a Trypsin-EDTA 10× solution (SAFC, Merck,) was added during 5 min on a stirrer, to detach cells, and then 4 mL of media was used to stop trypsin effect. After centrifugation (5 min at 300 rcf), cells were resuspended in 200 µL of media and deposited on glass slide for visualization.
Drug Treatments and Immunocytochemistry.
In order to fragment cells, staurosporin (Biotum, VWR) was first preheated for 30 min at 37°C. Cells were then incubated with staurosporine at 120 nM at 28°C for 1 h and staurosporine was kept in the solution during migration experiments. Nuclei were labeled with 1 µg.mL−1 Hoechst 33342 trihydrochloride trihydrate (Invitrogen, Thermo Fisher Scientific) 20 min before experiment and then rinsed with medium. For visualization of intracellular components by fluorescent staining techniques, fish keratocytes were rinsed three times with PBS (phosphate-buffered saline at pH: 7.4), fixed, permeabilized with a first incubation in 0.05% glutaraldehyde in association with 0.1% Triton X-100 during 1 min, and then rinsed with PBS followed by a second 10-min incubation in a 0.14% solution of glutaraldehyde. After permeabilization and fixation, the cells were blocked with a solution of 5% FBS. They were rinsed abundantly with PBS and incubated for 45 min at 37°C with Alexa Fluor 488 phalloidin (Invitrogen, 1:200) for staining the F-actin and 4′,6′-diamidino-2-phenylindole (DAPI; Invitrogen, 1:200) to visualize the nuclei. Coverslips were mounted with Slow Fade Gold Antifade (Molecular Probes, Invitrogen).
Flow Chamber Preparation.
Ultra-clean glass slides (25 × 75 um Nexterion cleanroom cleaned, SCHOTT) cut to a dimension of 20 × 25 mm and a sticky bottomless channel slide (sticky-Slide VI 0.4, Ibidi) were used for all experiments. For experiments of cell sorting by mechanotaxis phenotype, a 20 × 25-mm stencil of 250-µm-thick polydimethylsiloxane (PDMS) (Sterne Silicon Performance) was cut out with a 2.5 × 2.5-mm square opening in the middle. The stencil was deposited on the glass slides, and then a drop of 50 µL of cell suspension was deposited in the opening and let for 1 h at 28°C. The supernatant was removed with a micropipette, letting a few microliters to keep adherent cells in wet conditions. The PDMS sticker was then carefully removed, which resulted in getting a wet square with adherent cells on the glass slide. Finally, a sticky bottomless channel slide (sticky-Slide VI 0.4, Ibidi) was stuck on the glass slide by paying attention to align a channel on the wet square. The channel was filled with media immediately after and plugged to the pumping system. Continuous flow was provided by two 20 mL syringes half filled with media and set up on two syringe drivers (Nemesys S, Cetoni GmbH) equipped with two three-way valves and controlled by the software CETONI Elements (Cetoni GmbH) to provide unidirectional flow in the channels.
Microscopy.
Flow experiments were performed on an inverted Zeiss Z1 automated microscope (Carl Zeiss) equipped with a CoolSnap HQ CCD camera (Photometrics) and pE-300 white LED microscope illuminator (CoolLED) and driven by μManager (Edelstein. et al., Current Protocols. 2010). Transmission images were taken in phase contrast with a ×10/0.3 (EC Plan-Neofluar, Carl Zeiss) or a ×20/0.8 (Plan Apo-chromat, Carl Zeiss) objective, a ×0.5 lens (Camera adapter 60N-C 2/3 0.5×, and autofocus (Definite focus, Carl Zeiss). Multifield images were managed using the µManager grid tool. A Neofluar 63/1.25 antiflex (Carl Zeiss) was used for RICM mode, combined to a narrow band-pass filter (λ = 546 nm ± 12 nm). Confocal imaging was performed with a Nikon A1R HD25 motorized inverted microscope equipped with ×100 Plan Apo (numerical aperture, 1.45; oil immersion) objective and lasers that span the blue (457, 477, and 488 nm) and green (514 and 543 nm) spectral regions. Confocal images were recorded using small Z-depth increments (0.125 μm) and were processed using the NIS-Elements software. Exposure times and laser power were kept constant, and the acquired stack of images was deconvolved to remove the focus light.
Image Analysis.
Multifield images were stitched with the help of a Fiji homemade macro using the Pairwise Stitching plugin (Preibisch et al. Bioinformatics. 2009). To remove background, we divided the images by the median projection of the movies. Cell segmentation was done using a Sobel edges detector followed by thresholding. The Fiji plugin Trackmate (Tinevez et al. Methods. 2017) was used to track cells. Trajectory analysis was performed with a homemade MATLAB code (MATLAB software, The MathWorks). Observables such as positions and speed were accounted only for trajectories lasting more than 100 steps. The forward migration index of a cell, YFMI, was calculated by dividing the distance traveled in the Y axis direction by the total length of the trajectory. The average speed of a cell, V, was calculated by the ratio between the contour length of the trajectory and the corresponding time of migration. Cell directions were determined on three consecutive frames (i.e., time laps of 20 s), and cell direction changes were determined by comparing cell directions of two consecutive time points (i.e., separated by 10 s). In Fig. 5C, cell areas, were segmented using a Sobel edges detector followed by thresholding and extracted using the regionprops function from MATLAB. Cell rear areas, , were extracted by manual measurements in Fiji on transmission images. In Fig. 5E, cell directions were determined on three consecutive frames (i.e., time laps of 20 s), and direction changes were analyzed for each time step of 10 s. The events where cell directions crossed the axis of symmetry (which happened only for initial direction close to 0° and 180°) did not strictly correspond to either upstream or downstream turns and were removed from the statistics.
Supplementary Material
Appendix 01 (PDF)
Keratocytes orient mainly downstream under flow – Movie of crawling keratocytes displaying downstream phenotype at magnification x60 with superposition of phase contrast mode (gray) and reflection interference contrast microscopy RICM mode (green). The contrast was inverted in RICM images, so that bright green corresponds to the adhesion fingerprint. Shear stress was 60 dyn.cm-2.
A subpopulation of keratocytes displays upstream phenotype – Movie of crawling keratocytes at magnification ×20 in phase contrast mode showing a small fraction of upstream bounded cells. Shear stress was 60 dyn.cm-2.
Flow reversal experiment shows that cells have an intrinsic upstream or downstream phenotype– Movie showing downstream-bound and upstream-bound cells making U-turns after flow reversal at time t=5 min. Shear stress is 60 dyn.cm-2.
Cell sorting by phenotype of orientation under flow – Movies of a representative experiment of cells above (Top), inside (Middle), and below (Bottom) the seeding zone. Shear stress was 60 dyn.cm-2.
Fragments of keratocyte lamellipods migrate downstream – Movie of crawling keratocyte fragment at magnification ×60 with superposition of phase contrast mode (gray) and reflection interference contrast microscopy RICM mode (green). The contrast was inverted in RICM images so that bright green correspond to the adhesion fingerprint. Shear stress was 60 dyn.cm-2.
Large lamellipods of downstream bound cells are turned upside down upon flow reversal – Movie of crawling keratocytes at magnification ×20 in phase contrast mode with flow reversal at time 4:40 min:s. Shear stress was 60 dyn.cm-2.
Upstream-bound cells display fluctuations of lamellipod adhesion – Movie of crawling keratocytes with upstream phenotype at magnification ×60 with superposition of phase contrast mode (gray) and reflection interference contrast microscopy RICM mode (green). The contrast was inverted in RICM images so that bright green correspond to the adhesion fingerprint. Shear stress was 60 dyn.cm-2.
Acknowledgments
The work was supported by the French Agence Nationale de la Recherche (RECRUTE ANR-15-CE15-0022 and ILIAAD ANR-18-CE09-0029), the Region PACA, the Turing Centre for Living systems, and the Excellence Initiative of Aix-Marseille University –A*MIDEX, a French ‘‘Investissements d’Avenir’’ program.
Author contributions
V.S., S.G., M.-P.V., and O.T. designed research; V.S., A.R., and M.B.-P. performed research; I.M. contributed new reagents/analytic tools; V.S., F.M., M.-P.V., and O.T. analyzed data; O.T. developed the model; and O.T. wrote the paper.
Competing interests
The authors declare no competing interest.
Footnotes
This article is a PNAS Direct Submission. K.K. is a guest editor invited by the Editorial Board.
Data, Materials, and Software Availability
All study data are included in the article and/or SI Appendix.
Supporting Information
References
- 1.SenGupta S., Parent C. A., Bear J. E., The principles of directed cell migration. Nat. Rev. Mol. Cell Biol. 22, 529–547 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Carter S. B., Haptotaxis and the mechanism of cell motility. Nature 213, 256 (1967). [DOI] [PubMed] [Google Scholar]
- 3.Dineur E., Note sur la sensibilité des leucocytes à l’électricité. Bull Séances Soc Belge Microsc. 18, 113–118 (1891). [Google Scholar]
- 4.Blakemore R., Magnetotactic bacteria. Science 190, 377–379 (1975). [DOI] [PubMed] [Google Scholar]
- 5.Sunyer R., Trepat X., Durotaxis. Curr. Biol. 30, R383–R387 (2020). [DOI] [PubMed] [Google Scholar]
- 6.Valignat M.-P., Theodoly O., Gucciardi A., Hogg N., Lellouch A. C., T lymphocytes orient against the direction of fluid flow during LFA-1-mediated migration. Biophys. J. 104, 322–331 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Roy N. H., MacKay J. L., Robertson T. F., Hammer D. A., Burkhardt J. K., Crk adaptor proteins mediate actin-dependent T cell migration and mechanosensing induced by the integrin LFA-1. Sci. Signal. 11, eaat3178 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Wolf K., Müller R., Borgmann S., Bröcker E.-B., Friedl P., Amoeboid shape change and contact guidance: T-lymphocyte crawling through fibrillar collagen is independent of matrix remodeling by MMPs and other proteases. Blood 102, 3262–3269 (2003). [DOI] [PubMed] [Google Scholar]
- 9.Prentice-Mott H. V., et al. , Biased migration of confined neutrophil-like cells in asymmetric hydraulic environments. Proc. Natl. Acad. Sci. U.S.A. 110, 21006–21011 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Polacheck W. J., German A. E., Mammoto A., Ingber D. E., Kamm R. D., Mechanotransduction of fluid stresses governs 3D cell migration. Proc. Natl. Acad. Sci. U.S.A. 111, 2447–2452 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Ostrowski M. A., et al. , Microvascular endothelial cells migrate upstream and align against the shear stress field created by impinging flow. Biophys. J. 106, 366–374 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Iglesias P. A., Devreotes P. N., Navigating through models of chemotaxis. Curr. Opin. Cell Biol. 20, 35–40 (2008). [DOI] [PubMed] [Google Scholar]
- 13.Labernadie A., Trepat X., Sticking, steering, squeezing and shearing: Cell movements driven by heterotypic mechanical forces. Curr. Opin. Cell Biol. 54, 57–65 (2018). [DOI] [PubMed] [Google Scholar]
- 14.Zaidel-Bar R., Kam Z., Geiger B., Polarized downregulation of the paxillin-p130CAS-Rac1 pathway induced by shear flow. J. Cell Sci. 118, 3997–4007 (2005). [DOI] [PubMed] [Google Scholar]
- 15.Décavé E., et al. , Shear flow-induced motility of Dictyostelium discoideum cells on solid substrate. J. Cell Sci. 116, 4331–4343 (2003). [DOI] [PubMed] [Google Scholar]
- 16.Rainger G. E., Buckley C. D., Simmons D. L., Nash G. B., Neutrophils sense flow-generated stress and direct their migration through αVβ3-integrin. Am. J. Physiol. Heart Circ. Physiol. 276, H858–H864 (1999). [DOI] [PubMed] [Google Scholar]
- 17.Polacheck W. J., Charest J. L., Kamm R. D., Interstitial flow influences direction of tumor cell migration through competing mechanisms. Proc. Natl. Acad. Sci. U.S.A. 108, 11115–11120 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Steiner O., et al. , Differential roles for endothelial ICAM-1, ICAM-2, and VCAM-1 in shear-resistant t cell arrest, polarization, and directed crawling on blood–brain barrier Endothelium. J. Immunol. 185, 4846–4855 (2010). [DOI] [PubMed] [Google Scholar]
- 19.Robert P., et al. , Functional mapping of adhesiveness on live cells reveals how guidance phenotypes can emerge from complex spatiotemporal integrin regulation. Front. Bioeng. Biotechnol. 9, 625366 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Dominguez G. A., Anderson N. R., Hammer D. A., The direction of migration of T-lymphocytes under flow depends upon which adhesion receptors are engaged. Integr. Biol. 7, 345–355 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Buffone A., Anderson N. R., Hammer D. A., Migration against the direction of flow is LFA-1-dependent in human hematopoietic stem and progenitor cells. J. Cell Sci. 131, jcs205575 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Tedford K., et al. , The opposing forces of shear flow and sphingosine-1-phosphate control marginal zone B cell shuttling. Nat. Commun. 8, 2261 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Anderson N. R., Buffone A. Jr., Hammer D. A., T lymphocytes migrate upstream after completing the leukocyte adhesion cascade. Cell Adh. Migr. 13, 163–168 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Buffone A., Anderson N. R., Hammer D. A., Human neutrophils will crawl upstream on ICAM-1 If Mac-1 Is blocked. Biophys. J. 117, 1393–1404 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Kim S. H. J., Hammer D. A., Integrin crosstalk allows CD4+ T lymphocytes to continue migrating in the upstream direction after flow. Integr. Biol. 11, 384–393 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Roy N. H., et al. , LFA-1 signals to promote actin polymerization and upstream migration in T cells. J. Cell Sci. 133, jcs248328 (2020), 10.1101/2020.04.29.069302. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Hornung A., et al. , A bistable mechanism mediated by integrins controls mechanotaxis of leukocytes. Biophys. J. 118, 565–577 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Valignat M.-P., et al. , Lymphocytes can self-steer passively with wind vane uropods. Nat. Commun. 5, 5213 (2014). [DOI] [PubMed] [Google Scholar]
- 29.Mogilner A., Barnhart E. L., Keren K., Experiment, theory, and the keratocyte: An ode to a simple model for cell motility. Semin. Cell Dev. Biol. 100, 143–151 (2020). [DOI] [PubMed] [Google Scholar]
- 30.Keren K., et al. , Mechanism of shape determination in motile cells. Nature 453, 475–480 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Euteneuer U., Schliwa M., Persistent, directional motility of cells and cytoplasmic fragments in the absence of microtubules. Nature 310, 58–61 (1984). [DOI] [PubMed] [Google Scholar]
- 32.Smith L. A., Aranda-Espinoza H., Haun J. B., Dembo M., Hammer D. A., Neutrophil traction stresses are concentrated in the uropod during migration. Biophys. J. 92, L58–L60 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Bohnet S., Ananthakrishnan R., Mogilner A., Meister J. J., Verkhovsky A. B., Weak force stalls protrusion at the leading edge of the Lamellipodium. Biophys. J. 90, 1810–1820 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Price T. C., Slow linear shear flow past a hemispherical bump in a plane wall. Q. J. Mech. Appl. Math. 38, 93–104 (1985). [Google Scholar]
- 35.Hyman W. A., shear flow over a protrusion from a plane wall. J. Biomech. 5, 45–48 (1972). [DOI] [PubMed] [Google Scholar]
- 36.Ridley A. J., et al. , Cell migration: Integrating signals from front to back. Science 302, 1704–1709 (2003). [DOI] [PubMed] [Google Scholar]
- 37.Bartholomäus I., et al. , Effector T cell interactions with meningeal vascular structures in nascent autoimmune CNS lesions. Nature 462, 94–98 (2009). [DOI] [PubMed] [Google Scholar]
- 38.Artemenko Y., Axiotakis L., Borleis J., Iglesias P. A., Devreotes P. N., Chemical and mechanical stimuli act on common signal transduction and cytoskeletal networks. Proc. Natl. Acad. Sci. U.S.A. 113, E7500–E7509 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Dupont S., et al. , Role of YAP/TAZ in mechanotransduction. Nature 474, 179–183 (2011). [DOI] [PubMed] [Google Scholar]
- 40.De Belly H., Paluch E. K., Chalut K. J., Interplay between mechanics and signalling in regulating cell fate. Nat. Rev. Mol. Cell Biol. 23, 465–480 (2022). [DOI] [PubMed] [Google Scholar]
- 41.Gudipaty S. A., et al. , Mechanical stretch triggers rapid epithelial cell division through Piezo1. Nature 543, 118–121 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Dixit N., Yamayoshi I., Nazarian A., Simon S. I., Migrational guidance of neutrophils is mechanotransduced via high-affinity LFA-1 and calcium flux. J. Immunol. 187, 472–481 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Allen G. M., et al. , Cell mechanics at the rear act to steer the direction of cell migration. Cell Syst. 11, 286–299.e4 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Guyon E., Hulin J. P., Petit L., Mitescu C. D., Physical Hydrodynamics (Oxford Univ Press, ed. 2, 2015). [Google Scholar]
- 45.Li G., Kolomenskiy D., Liu H., Thiria B., Godoy-Diana R., Hydrodynamical fingerprint of a neighbour in a fish lateral line. Front. Robot. AI 9, 825889 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Appendix 01 (PDF)
Keratocytes orient mainly downstream under flow – Movie of crawling keratocytes displaying downstream phenotype at magnification x60 with superposition of phase contrast mode (gray) and reflection interference contrast microscopy RICM mode (green). The contrast was inverted in RICM images, so that bright green corresponds to the adhesion fingerprint. Shear stress was 60 dyn.cm-2.
A subpopulation of keratocytes displays upstream phenotype – Movie of crawling keratocytes at magnification ×20 in phase contrast mode showing a small fraction of upstream bounded cells. Shear stress was 60 dyn.cm-2.
Flow reversal experiment shows that cells have an intrinsic upstream or downstream phenotype– Movie showing downstream-bound and upstream-bound cells making U-turns after flow reversal at time t=5 min. Shear stress is 60 dyn.cm-2.
Cell sorting by phenotype of orientation under flow – Movies of a representative experiment of cells above (Top), inside (Middle), and below (Bottom) the seeding zone. Shear stress was 60 dyn.cm-2.
Fragments of keratocyte lamellipods migrate downstream – Movie of crawling keratocyte fragment at magnification ×60 with superposition of phase contrast mode (gray) and reflection interference contrast microscopy RICM mode (green). The contrast was inverted in RICM images so that bright green correspond to the adhesion fingerprint. Shear stress was 60 dyn.cm-2.
Large lamellipods of downstream bound cells are turned upside down upon flow reversal – Movie of crawling keratocytes at magnification ×20 in phase contrast mode with flow reversal at time 4:40 min:s. Shear stress was 60 dyn.cm-2.
Upstream-bound cells display fluctuations of lamellipod adhesion – Movie of crawling keratocytes with upstream phenotype at magnification ×60 with superposition of phase contrast mode (gray) and reflection interference contrast microscopy RICM mode (green). The contrast was inverted in RICM images so that bright green correspond to the adhesion fingerprint. Shear stress was 60 dyn.cm-2.
Data Availability Statement
All study data are included in the article and/or SI Appendix.