Abstract
Objective
Prognostic outcomes related to hospital admissions typically do not suffer from censoring, and can be modeled either categorically or as time-to-event. Competing events are common but often ignored. We compared the performance of static and dynamic random forest (RF) models to predict the risk of central line-associated bloodstream infections (CLABSI) using different outcome operationalizations.
Methods
We included data from 27,478 admissions to the University Hospitals Leuven, covering 30,862 catheter episodes (970 CLABSI, 1466 deaths and 28,426 discharges) to build static and dynamic RF models for binary (CLABSI vs no CLABSI), multinomial (CLABSI, discharge, death or no event), survival (time to CLABSI) and competing risks (time to CLABSI, discharge or death) outcomes to predict the 7-day CLABSI risk. Static models used information at the onset of the catheter episode, while dynamic models updated predictions daily for 30 days (landmark 0-30). We evaluated model performance across 100 train/test splits.
Results
Performance of binary, multinomial and competing risks models was similar: AUROC was 0.74 for predictions at catheter onset, rose to 0.77 for predictions at landmark 5, and decreased thereafter. Survival models overestimated the risk of CLABSI (E:O ratios between 1.2 and 1.6), and had AUROCs about 0.01 lower than other models. Binary and multinomial models had lowest computation times. Models including multiple outcome events (multinomial and competing risks) display a different internal structure compared to binary and survival models, choosing different variables for early splits in trees.
Discussion and conclusion
In the absence of censoring, complex modelling choices do not considerably improve the predictive performance compared to a binary model for CLABSI prediction in our studied settings. Survival models censoring the competing events at their time of occurrence should be avoided.
Supplementary information
The online version contains supplementary material available at 10.1186/s41512-025-00194-8.
Keywords: Random forests, Competing risks, Survival, CLABSI, EHR, Dynamic prediction
Background and significance
Electronic Health Records (EHR) are commonly used to develop prediction models using statistical or machine learning (ML) methods. Many models utilizing EHR data focus on acute clinical events during hospital or ICU admissions, such as sepsis [1–4], ventilator-associated pneumonia [5] and acute kidney injury [6]. These models vary with regards to the prediction time point: static (e.g., early detection at admission) or dynamic models (predictions are updated at different times during the patient follow up). Models using EHR data are often built against surveillance event definitions. In contrast to outcomes recorded after patient discharge (such as ICD codes), the time on the patient timeline when the clinical event of interest has occurred is typically known whenever surveillance event definitions are used. This makes time-to-event models, also known as survival models, an attractive modeling choice. The outcome of interest is typically a specific event (e.g., sepsis), but competing events may preclude the occurrence of the event of interest (e.g., being discharged in good health conditions or dying of other causes). Competing events are regularly ignored during model building, which may be detrimental to the models’ predictive performance according to statistical literature [7].
A particularity of EHR data is that patients are normally followed up until discharge; therefore in-hospital outcomes based on EHR data are not subject to loss to follow up and the outcome can be modeled either categorically (i.e., as binary or multinomial) or using time-to-event approaches. While survival or competing risks models are the preferred methods when censoring is present, the absence of censoring does not render these models invalid; it only simplifies the settings in which these models operate.
Random forests (RFs) [8] are ensemble machine learning models, initially proposed for regression and classification. They have been extended for survival [9] and competing risks [10] settings, with adapted split rules for the survival outcome (survival difference between the left and right daughter nodes) or competing risks outcome (cause-specific cumulative hazard function or cumulative incidence function).
Objective
We perform a methodological comparison of random forest models built against different outcome types (binary, multinomial, survival and competing risks) for predicting central line-associated bloodstream infection (CLABSI). CLABSI is a hospital acquired infection defined as a bloodstream infection in patients with a central line that is not related to an infection at another site. CLABSI prediction models are built primarily on EHR data and most models use a binary outcome without a fixed time horizon (CLABSI event at any time during adm [11]. Most models are static, making predictions at a fiission) or survival models not accounting for competing risks [xed moment in time (usually at catheter placement), without updating the predictions throughout the patient’s hospitalization.
The question we aim to answer is whether incorporating more information in the outcome (exact event times for survival and competing risks; additional events in multinomial and competing risks models) leads to improved performance compared to the binary model to predict the 7 day risk of CLABSI. We build both static and dynamic models and consider discharge, catheter removal and patient death as competing events that preclude the occurrence of the event of interest.
Data and methods
Study design and participants
Patient data are extracted from the EHR system of the University Hospitals Leuven for hospital admissions in the period January 2012–December 2013. We included patient admissions with registration of one or multiple central lines: centrally inserted central catheter (CICC), tunneled cuffed and non-cuffed central venous catheter, port catheter (totally implanted vascular access devices (TIVAD)), peripherally inserted central catheter (PICC) and dialysis catheter. The terms “central line” and “catheter” will be used interchangeably. Patients with only a dialysis catheter (and no other catheter type) were included only if they were admitted to ICU (due to the data extraction constraint). Because the neonatology department did not record catheters in the EHR system before October 2013, 260 neonates admissions have been excluded. The dataset consists of 27,478 hospital admissions after excluding neonates.
The following levels of the outcome are considered:
CLABSI: any laboratory-confirmed bloodstream infection (LC-BSI) during hospital admission for a patient with central line or within 48 h after the central line removal that is not present in the first 48 h after admission, that is not a secondary infection, is not a skin contamination and is not a mucosal barrier injury LC-BSI. The CLABSI definition has been calculated retrospectively based on the extracted data following the Sciensano definition published in 2019 [12].
Discharge: hospital discharge or 48 h after catheter removal, whichever happens first. According to the Sciensano definition, the patient remains at risk of CLABSI for 48 h after catheter removal.
Death: either the first contact with palliative care during admission, transfer to palliative care or patient death, whichever happens first. Patients stop being closely monitored in palliative care and predictions on this ward are not actionable.
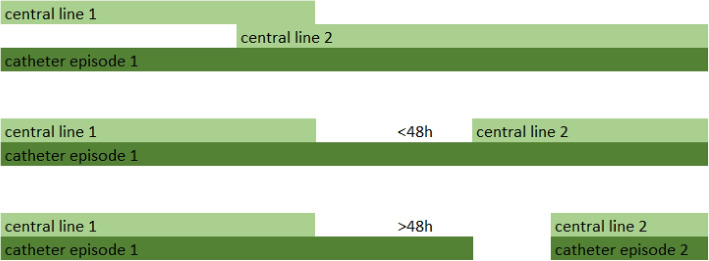
Patient admissions are split in catheter episodes. A catheter episode starts at catheter placement or at the registration of the first catheter observation during that admission (e.g., in case of admission to hospital with a long-term catheter) and ends when no catheter observation is made for 48 h or when discharge, death or CLABSI occurs. In case of multiple concomitant catheters (e.g., admission with a long-term catheter and placement of another central venous catheter during hospitalization), these are grouped in the same catheter episode if they are overlapping or if there is a time gap of less than 48 h between removal of one catheter and placement of a new one (Fig. 1).
Fig. 1.
Catheter episodes
A catheter episode is further split in landmarks (LMs). The exact time of the first catheter observation is considered landmark 0 (LM0). Subsequent landmarks are created every 24 h (LM1 is 24 h after LM0, LM2 48 h after LM0, and so on up to LM30); each LM corresponds to a catheter-day in the catheter episode. Predictions are made every 24 h. The landmark dataset contains in rows each LM and in columns the features which may have varying values on different landmarks. An excerpt of the dataset is presented in Supplementary material 1.
The dataset consists of 27,478 admissions, 30,862 catheter episodes with complete follow-up for all event types: 970 CLABSI, 1466 deaths and 28,426 discharges. There are in total 227,928 landmarks.
Prediction horizon and outcome types
The risk of CLABSI in any of the following 7 days is predicted at each landmark. We will represent the outcome in four different ways:
Binary: CLABSI vs. no CLABSI within 7 days.
Multinomial: CLABSI, death, discharge and no event within 7 days.
Survival: status 1 if CLABSI occurs and 0 (censored) if no CLABSI occurs; the event time is the time of CLABSI occurrence or the censoring time.
Competing risks (CR): CLABSI, death and discharge with their event times.
Features
The dataset consists of 302 baseline (onset of catheter episode) and time-varying features comprising admission and demographics, medication, laboratory test results, comorbidities, vital signs and catheter registrations. The features have been reviewed by three clinical experts (an infection preventionist, a clinical nurse specialist in vascular access and a critical care physician) and assessed as important or unimportant for CLABSI prediction. Out of the complete set of features, 21 have been selected for the model building, based on the clinical review as well as their inclusion in other CLABSI prediction studies [11]. The features included in the model and the patient characteristics at baseline are presented in Table 1. Full features descriptions are available in Supplementary material 2.
Table 1.
Patient characteristics at baseline using the features included in the models (n = 30,862 catheter episodes); mean (sd) for continuous variables, before missing data imputation; n (%) for categorical variables. Patients can have two different catheter types simultaneously with different locations, therefore catheter type and location have been coded as binary and not categorical features with multiple categories
| Feature name | Description | Statistic | Total | CLABSI | Death | Discharge |
|---|---|---|---|---|---|---|
| n = 30,862 | n = 970 | n = 1466 | n = 28,426 | |||
| CVC | Catheter type CICC | 0, n(%) | 17,264 (55.9) | 340 (35.1) | 872 (59.5) | 16,052 (56.5) |
| 1, n(%) | 13,598 (44.1) | 630 (64.9) | 594 (40.5) | 12,374 (43.5) | ||
| Port catheter | Catheter type TIVAD | 0, n(%) | 16,855 (54.6) | 768 (79.2) | 744 (50.8) | 15,343 (54.0) |
| 1, n(%) | 14,007 (45.4) | 202 (20.8) | 722 (49.2) | 13,083 (46.0) | ||
| Tunneled CVC | Catheter type tc-CICC or t-CICC | 0, n(%) | 29,489 (95.6) | 870 (89.7) | 1426 (97.3) | 27,193 (95.7) |
| 1, n(%) | 1373 (4.4) | 100 (10.3) | 40 (2.7) | 1233 (4.3) | ||
| PICC | Catheter type PICC | 0, n(%) | 29,579 (95.8) | 941 (97.0) | 1380 (94.1) | 27,258 (95.9) |
| 1, n(%) | 1283 (4.2) | 29 (3.0) | 86 (5.9) | 1168 (4.1) | ||
| Jugular | Catheter location jugular | 0, n(%) | 14,104 (45.7) | 581 (59.9) | 592 (40.4) | 12,931 (45.5) |
| 1, n(%) | 16,758 (54.3) | 389 (40.1) | 874 (59.6) | 15495 (54.5) | ||
| Subclavian | Catheter location subclavian | 0, n(%) | 18,793 (60.9) | 448 (46.2) | 1026 (70.0) | 17,319 (60.9) |
| 1, n(%) | 12,069 (39.1) | 522 (53.8) | 440 (30.0) | 11,107 (39.1) | ||
| TPN | Total parenteral nutrition (TPN) order in previous 7 days | 0, n(%) | 28,494 (92.3) | 686 (70.7) | 1292 (88.1) | 26,516 (93.3) |
| 1, n(%) | 2368 (7.7) | 284 (29.3) | 174 (11.9) | 1910 (6.7) | ||
| AB | Antibacterials order in previous 7 days | 0, n(%) | 13,060 (42.3) | 279 (28.8) | 563 (38.4) | 12,218 (43.0) |
| 1, n(%) | 17,802 (57.7) | 691 (71.2) | 903 (61.6) | 16,208 (57.0) | ||
| Chemotherapy | Antineoplastic agents order in previous 7 days | 0, n(%) | 24,720 (80.1) | 897 (92.5) | 1410 (96.2) | 22,413 (78.8) |
| 1, n(%) | 6142 (19.9) | 73 (7.5) | 56 (3.8) | 6013 (21.2) | ||
| CLABSI history | CLABSI history | 0, n(%) | 30,304 (98.2) | 940 (96.9) | 1434 (97.8) | 27,930 (98.3) |
| 1, n(%) | 558 (1.8) | 30 (3.1) | 32 (2.2) | 496 (1.7) | ||
| Tumor history | Tumor history | 0, n(%) | 14,078 (45.6) | 598 (61.6) | 634 (43.2) | 12,846 (45.2) |
| 1, n(%) | 16,784 (54.4) | 372 (38.4) | 832 (56.8) | 15,580 (54.8) | ||
| Temperature | Max. temperature in last 24 h [°C] | Mean (SD) | 36.8 (0.8) | 37.0 (0.9) | 37.0 (0.9) | 36.8 (0.8) |
| Systolic BP | Last systolic blood pressure in last 24 h [mmHg] | Mean (SD) | 125.8 (22.3) | 123.0 (23.5) | 121.3 (25.7) | 126.1 (22.1) |
| WBC | White blood cell count in last 24 h [10**9/L] | Mean (SD) | 9.4 (8.4) | 10.4 (12.1) | 11.7 (13.5) | 9.2 (7.7) |
| Lymphoma history | Lymphoma history | 0, n(%) | 29,480 (95.5) | 928 (95.7) | 1387 (94.6) | 27,165 (95.6) |
| 1, n(%) | 1382 (4.5) | 42 (4.3) | 79 (5.4) | 1261 (4.4) | ||
| Transplant history | Transplant history | 0, n(%) | 29,355 (95.1) | 904 (93.2) | 1391 (94.9) | 27,060 (95.2) |
| 1, n(%) | 1507 (4.9) | 66 (6.8) | 75 (5.1) | 1366 (4.8) | ||
| Other infection than BSI | Other infection than BSI in previous 17 days | 0, n(%) | 27768 (90.0) | 847 (87.3) | 1252 (85.4) | 25,669 (90.3) |
| 1, n(%) | 3094 (10.0) | 123 (12.7) | 214 (14.6) | 2757 (9.7) | ||
| CRP | C-reactive protein unit in last 24 h [mg/L] | Mean (SD) | 48.7 (71.9) | 59.3 (84.0) | 95.3 (96.6) | 45.1 (68.1) |
| Admission source: home | Admission source: home | 0, n(%) | 3728 (12.3) | 240 (24.9) | 344 (23.7) | 3144 (11.2) |
| 1, n(%) | 26,637 (87.7) | 725 (75.1) | 1107 (76.3) | 24,805 (88.8) | ||
| MV | Mechanical ventilation in last 24 h | 0, n(%) | 29,352 (95.1) | 872 (89.9) | 1253 (85.5) | 27,227 (95.8) |
| 1, n(%) | 1510 (4.9) | 98 (10.1) | 213 (14.5) | 1199 (4.2) | ||
| ICU | Patient currently in ICU (intensive care unit) ward | 0, n(%) | 25,807 (83.6) | 683 (70.4) | 973 (66.4) | 24,151 (85.0) |
| 1, n(%) | 5055 (16.4) | 287 (29.6) | 493 (33.6) | 4275 (15.0) | ||
| Days to event | Days to event | Mean (SD) | 7.3 (9.4) | 13.0 (14.6) | 9.8 (13.6) | 7.0 (8.8) |
Train/test split
One hundred random train/test splits are generated on the landmark dataset, keeping two thirds of the hospital admissions for training and one third for test, so that a full admission (with all its catheter episodes and all its landmarks) falls entirely in train set or entirely in the test set. Baseline datasets have then been generated by filtering the dynamic datasets for LM0. Missing data have been imputed using a combination of mean/mode imputation, normal value imputation and the missForestPredict algorithm [13] (Supplementary material 4). The average number and proportion of events in the baseline and dynamic training and test sets are presented in Table 2. Cumulative incidence functions (CIF) for all events are presented in Supplementary material 3.
Table 2.
Average number and average proportion of events in train and test sets; for baseline datasets the averaging is done over all catheter episodes; for dynamic datasets the averaging is done over all landmarks
| Baseline/dynamic | Horizon | Train/test | CLABSI, n (%) | Death, n (%) | Discharge, n (%) | No event until horizon, n (%) |
|---|---|---|---|---|---|---|
| Baseline | Any | Train | 646 (3.1%) | 977 (4.7%) | 18947 (92.1%) | 0 (0%) by definition |
| Baseline | Any | Test | 324 (3.1%) | 489 (4.8%) | 9479 (92.1%) | 0 (0%) by definition |
| Baseline | 7 days | Train | 269 (1.3%) | 558 (2.7%) | 13039 (63.4%) | 6704 (32.6%) |
| Baseline | 7 days | Test | 135 (1.3%) | 279 (2.7%) | 6522 (63.4%) | 3356 (32.6%) |
| Dynamic | Any | Train | 8700 (5.4%) | 10050 (6.2%) | 143264 (88.4%) | 0 (0%) by definition |
| Dynamic | Any | Test | 4376 (5.4%) | 5078 (6.3%) | 71716 (88.4%) | 0 (0%) by definition |
| Dynamic | 7 days | Train | 1152 (0.7%) | 1905 (1.2%) | 48327 (29.8%) | 110631 (68.3%) |
| Dynamic | 7 days | Test | 584 (0.7%) | 945 (1.2%) | 24176 (29.8%) | 55464 (68.3%) |
Static and dynamic model building using random forests
On each imputed baseline and dynamic training set, RF models are trained for the different outcome types (binary, multinomial, survival and competing risks). Baseline or static models are built on the baseline datasets (only LM0 of each catheter episode) and dynamic models are built on the landmark dataset. Static models consider each catheter episode as an independent observation, while 8.2% of the admissions have more than one catheter episode. The dynamic models are built considering each landmark in each catheter episode an independent observation; the landmark number is included in the dynamic model, allowing the dynamic models to account for time effects as well as interactions with time. For static and dynamic model tuning, all catheter episodes belonging to an admission are assigned to either the training or validation data sample.
Random forest models are built using the randomforestSRC package [14]. Each tree is built on an “in-bag” (a sample of the training set) and evaluated on an “out-of-bag” (the remaining observations in the train set that are not in-bag) for hyperparameter tuning. The in-bags are created by sampling complete admissions with all their catheter episodes, so that an admission falls completely in-bag or completely out-of-bag. Sampling is done with replacement (bootstraps of size equal to the number of admissions) for static models and without replacement (subsamples with tuned subsample size between 30% and 80% of the admissions) for dynamic models; we consider that when data are large enough [15] we can build the trees on subsamples from the data; because of the limited number of events in the baseline data, we consider bootstraps a more appropriate strategy. The number of trees is fixed to 1000 trees, considering this as large enough and unnecessary to tune [15]. We thus create 1000 in-bags for each of the 100 training sets. Because randomforestSRC package imposes the limitation that all in-bags for the 1000 trees must have the same size and sampling by admission id will not result in equal in-bag sizes as not all admissions have an equal numbers of catheter episodes (and landmarks for the dynamic models), we further adjusted the in-bags to the minimum size (minsize) of all the 1000 inbags for all trees by randomly sampling out some catheter episodes and/or landmarks, which will consequently fall out-of-bag. The resulting subsample size for in-bags for dynamic models ranges between 43724 for 30% subsample size and 119,865 for 80% subsample size. This procedure had negligible effects on model performance (Supplementary material 5).
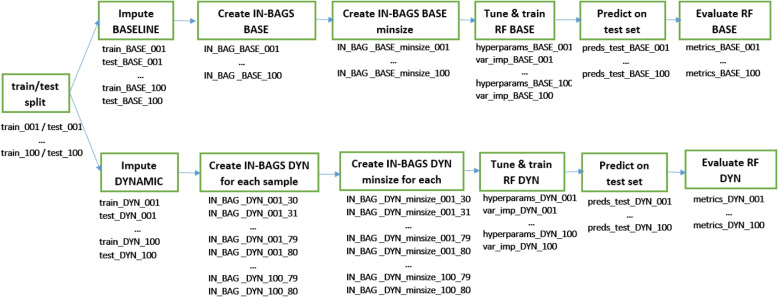
The tuned hyperparameters are the number of variables selected at each split (mtry) and the minimum size of a terminal node (nodesize) for both static and dynamic models. Additionally for dynamic models, the subsample size is tuned. Model tuning is based on the out-of-bag binary logloss for next 7 days prediction to allow all models to perform at their best for the outcome of interest. Model-based optimization tuning is performed using the mlrMBO R package [16]. (details in the Supplementary material 6). The best hyperparameters are chosen and a final RF model is built using these hyperparameters. The hyperparameter values used to build the final model, as well as a variable importance measure (the minimum depth of the maximal subtree [17]) are saved. The runtimes for model tuning, final model building and prediction on the test set are logged. The pipeline is schematically presented in Fig. 2.
Fig. 2.
Model building pipeline
Survival and competing risks models are unfeasible to train on a large dataset when using all event times. We have manipulated the event times for all events (CLABSI, death, and discharge) to speed up computations by discretizing the event times and applying administrative censoring [18]:
Discretized event times: the split statistics [19] are calculated for all event times present in the dataset which proves computationally inefficient. To considerably speed up computations, event times have been discretized using ceiling(t), e.g., an event happening at day 6.1 is considered to have happened at time 7. This approach shifts events into the future rather than the past to prevent time leaks. For instance, rounding 6.1 down to 6 would imply having knowledge at day 6 of an event that was only observed later.
Administrative censoring: we have applied artificial censoring as suggested by Van Houwelingen and Putter [18] by considering catheter episodes with events after a specific time t as censored. Two options are used for administrative censoring: (1) at day 7 since landmark time (the time of interest for the predictions) or (2) at day 30 since landmark time (92% of the events happen in the first 30 days after the start of the catheter episode; we consider it close to no administrative censoring).
Additional considerations have been implemented for survival and competing risks models:
Censoring (for survival models): for survival models we use two types of censoring for the competing events (death and discharge): (1) censoring at event time, e.g.: a discharge happening at day 5 is censored at time 5 (surv7 d and surv30 d models in Table 3); (2) censoring at day 7 since landmark time all competing events that happened before day 7 since landmark time, e.g., a discharge happening at time 5 is censored at time 7, keeping in the risk set catheter episodes with competing events until our time of interest, as done in Fine-Gray models [20] (surv7 d_cens7 and surv30 d_cens7 in Table 3). Alternatively, competing events could be censored beyond the time of interest, e.g., at day 30. However, we limit the analysis strictly up to the time of interest.
Split rule (for CR models): the two split rules available for competing risks models [19] are compared: (1) “logrank”, based on the difference in cause-specific hazard function and advised when the interest lies in a specific event and (2) “logrankCR” based on the difference in event-specific cumulative incidence and advised for prediction settings [19].
Cause (for CR models): when splitting a node in a competing risks model, the split-statistics weight by default all events equally. We compare: (1) the default equal weighting of events with (2) custom weighting (specified in parameter “cause”) using weight 1 for CLABSI and 0 for the other events (death and discharge outcome levels will not be used in determining tree splits).cm
Table 3.
Models
| Model name | Outcome type | Splitrule | Other hyperparameters/options | Static model | Dynamic model |
|---|---|---|---|---|---|
| bin | Binary | gini | Yes | Yes | |
| multinom | Multinomial | gini | Yes | Yes | |
| surv7 d | Survival | logrank | Administrative censoring at day 7; Censoring death and discharge at event time | Yes | Yes |
| surv7 d_cens7 | Survival | logrank | Administrative censoring at day 7; Censoring death and discharge at time 7 | Yes | Yes |
| surv30 d | Survival | logrank | Administrative censoring at day 30; Censoring death and discharge at event time | Yes | No |
| surv30 d_cens7 | Survival | logrank | Administrative censoring at day 30; Censoring death and discharge at time 7 | Yes | No |
| CR7 d_LRCR_c_1 | Competing risks | logrankCR | cause = 1 (CLABSI); Administrative censoring at day 7 | Yes | Yes |
| CR7 d_LR_c_1 | Competing risks | logrank | cause = 1 (CLABSI); Administrative censoring at day 7 | Yes | Yes |
| CR7 d_LRCR_c_all | Competing risks | logrankCR | cause = default (all events have equal weights); Administrative censoring at day 7 | Yes | Yes |
| CR7 d_LR_c_all | Competing risks | logrank | cause = default (all events have equal weights); Administrative censoring at day 7 | Yes | Yes |
| CR30 d_LRCR_c_1 | Competing risks | logrankCR | cause = 1 (CLABSI); Administrative censoring at day 30 | Yes | No |
| CR30 d_LR_c_1 | Competing risks | logrank | cause = 1 (CLABSI); Administrative censoring at day 30 | Yes | No |
| CR30 d_LRCR_c_all | Competing risks | logrankCR | cause = default (all events have equal weights); Administrative censoring at day 30 | Yes | No |
| CR30 d_LR_c_all | Competing risks | logrank | cause = default (all events have equal weights); Administrative censoring at day 30 | Yes | No |
The overview of all models is presented in Table 3. We compare 14 static models and 8 dynamic models. We chose not to run the dynamic models with administrative censoring at day 30 because of increased computation time.
Models tuning, building and predictions have been run on a high-performance computing cluster using 36 cores and 128 GB RAM. R version 4.2.1 and randomForestSRC 3.2.2 have been used to build the models.
Model evaluation
Predictions are made on the test sets for each of the model types. We retain the predicted risks of developing CLABSI in any of the next 7 days. We assume CLABSI risk within 7 days is the only outcome of clinical interest and the users of the model are not interested in predictions with other prediction horizons, nor are they interested in prediction of additional events (death or discharge). Survival models yield as predictions the survival probabilities for all time horizons with events present in the training dataset. For instance, considering the discretized event times and administrative censoring at day 30, predictions will cover each time point from day 1 to day 30, if at least an event occurred at each day.. We retain only the predictions for the time horizon of interest: . Competing risks models predict the cumulative incidence function conditional on predictors and we retain the predicted CIF of CLABSI at day 7.
Following metrics are evaluated on each test set: AUPRC (area under the precision recall curve), AUROC (Area Under the ROC curve), BSS (Brier Skill Score, the Brier Score divided by a reference Brier Score of a “no skill learner” that predicts the class prevalence), E:O ratio (the mean of predicted risks divided by the mean of observed binary events), calibration slope (calculated by regressing the true binary outcome on the logit of the predicted risks [21]) and ECI (Estimated Calibration Index; the mean squared difference between the predicted probabilities and the predicted probabilities obtained with a loess fit of the observed outcome on the predicted risks, multiplied by 100 [22]). For dynamic models, time-dependent metrics (metrics calculated at each LM) are presented. The median and interquartile range (IQR) for each metric over the 100 test sets are compared.
Code availability
The code used for model tuning, prediction and model evaluation is available at: https://github.com/sibipx/CLABSI_compare_RFSRC_models.
Results
Predictive performance for static models
Figure 3 and Supplementary materials 7 and 10 show the performance of the static models. Survival models with competing events censored at their occurrence time (surv7 d and surv30 d) show overestimated predicted risks (median E:O ratio of 1.44 and 1.47 respectively, compared to values between 0.99 and 1.00 for the other models) and poorer discrimination (median AUROC 0.729 for surv7 d and 0.724 for surv30 d, compared to AUROC between 0.735 and 0.742 for the other models). However, if individuals experiencing competing risks are kept in the risk set by censoring the event at the time of interest for predictions (surv7 d_cens7 and surv30 d_cens7 models), the performance becomes comparable to other models: median E:O ratio of 1.00 and AUROC of 0.742 and 0.739 respectively.
Fig. 3.
Prediction performance for static models. From left to right, separated by vertical lines: binary outcome model, multinomial outcome model, survival models, competing risk models. Models that consider all outcome classes to determine splits are displayed in blue, models that only consider CLABSI to determine splits are displayed in red
Models using all outcome levels (multinomial, CR7 d_LRCR_c_all, CR7 d_LR_c_all, CR30 d_LRCR_c_all, CR30 d_LR_c_all) show slightly higher AUPRC, despite slight miscalibration visible in the ECI, but with no noticeable difference in AUROC. These models venture into predicting higher risks than the other models and these larger predictions lead to miscalibration (Supplementary material 7 and 10) but better discrimination. Despite small differences in performance metrics, the internal structure of these models is different. Figure 4 presents the minimal depth of the maximal subtree [17], which is the depth in a tree on which the first split is made on a variable , averaged over all trees in the forest. The lowest possible value is 0 (root node split). Chemotherapy, antibiotics and CRP features are selected at first splits for models using all outcome levels, while binary and survival models favor TPN at early splits. These models also differ in hyperparameter values and predicted risk distributions (Supplementary material 7).
Fig. 4.
Feature minimal depth for static (baseline) and dynamic models. Includes only a subset of “important” features for which the median minimal depth is less than 2 in at least one model type. Lower minimal depths indicate more important variables. The minimal depth for all features is included in Supplementary material 7. Models that consider all outcome classes to determine splits are in blue, models that only consider CLABSI to determine splits are in red
The choice for administrative censoring for survival and CR model (day 7 or day 30) or the splitrule used by CR models (logrank or logrankCR) did not yield any visible difference.
Predictive performance for dynamic models
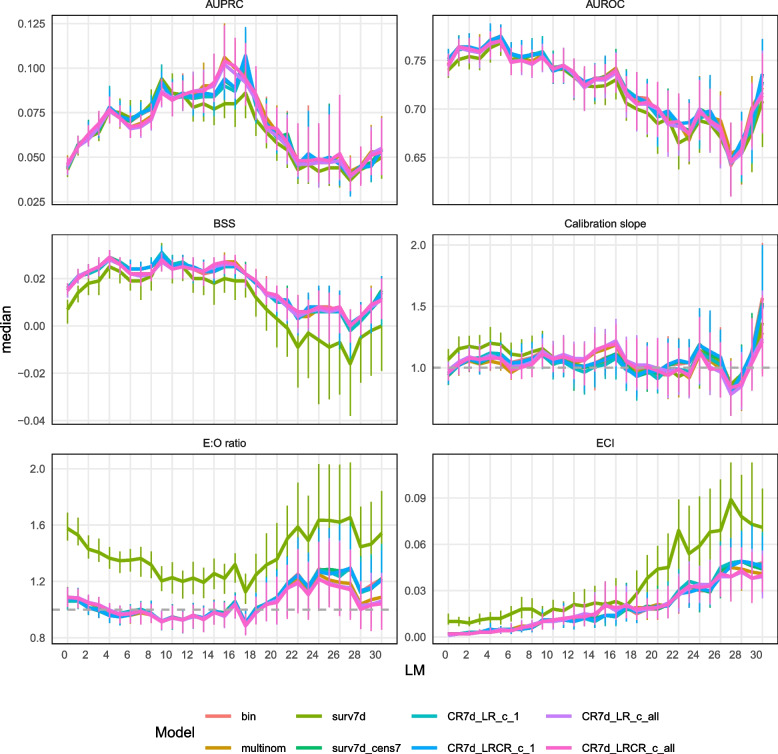
Figure 5 and Supplementary materials 8 and 11 show the dynamic models’ performance. All models reach their maximum AUROC at LM5. Similar to static models, the survival model with competing events censored at their occurrence time (surv7 d) shows overestimated predicted risks (median E:O ratio of 1.58 at LM0 and 1.35 at LM5, compared to values between 1.06 and 1.09 at LM0 and between 0.95 and 0.97 at LM5 for the other models) and slightly poorer discrimination (median AUROC 0.740 at LM0 and 0.768 at LM5, compared to AUROC between 0.744 and 0.752 at LM 0 and 0.770 and 0.775 at LM 5 for the other models). Censoring the competing event at the time of interest for predictions instead of at its event time (surv7 d_cens7 model) corrects this loss of calibration and discrimination. The models using multiple outcome levels choose at the first splits in the trees antibiotics, other infection than BSI and ICU (Fig. 4), while the other models favor TPN at early splits. They also differ in tuned hyperparameter values but do not exhibit an obvious difference in predicted risk distribution (Supplementary material 8) or in performance metrics. Dynamic models perform better than static models at LM0 in terms of discrimination (AUROC) and BSS, but worse in terms of calibration (Supplementary material 7).
Fig. 5.
Prediction performance for dynamic models–time dependent metrics. The median value of each metric is plotted over time (landmark) and the vertical bars indicate the IQR
Computational speed
The runtimes are presented in Fig. 6 and Supplementary material 9. The tuning time increases with model complexity, with binary, multinomial and the survival model with administrative censoring at day 7 and event censoring at day 7 being the fastest for both static and dynamic models; censoring at a later time (30 days) produces higher runtimes for static models and competing risks models take generally longest to tune. The runtimes vary less for the final model building, probably depending more on the final hyperparameter values. The prediction times also increase with model complexity but are fast for all models, with a median of less than one second for an entire baseline test set (on average slightly more than 10,000 observations) and less than two seconds for a dynamic test set (on average slightly more than 80,000 observations).
Fig. 6.
Runtimes for static (baseline) and dynamic models
Discussion
Survival and competing risks models are not widely used in machine learning prediction studies, and even less so on EHR data [23]. To our knowledge no other study compared RF models under competing risks settings. We compared different modelling options (binary, multinomial, survival, and competing risks outcome) for building static and dynamic random forest models for predicting the 7 days CLABSI risk using the randomforestSRC R package.
In our settings, complex models did not display a competitive advantage in terms of model performance. Moreover, complex models were slower to tune. Binary classification models remain the simplest choice for model building, implemented in a wide range of software libraries. Survival RF models that censor the competing event at its time of occurrence yield inferior calibration and discrimination compared to all the other modelling choices. Keeping the observations with competing events in the risk set until the prediction horizon, as done in Fine-Gray models [24], provides reliable estimates of the cumulative incidence function and superior prediction performance. This finding is potentially valuable for researchers with interest in predictions on multiple time horizons but unable to build a competing risks model due to software limitations. For instance, the ranger R package [25] supports survival models but not competing risks models; this might be the situation for other model choices or software libraries.
A companion study using regression models on the same dataset also found that binary, multinomial and competing risk models had similar performance [26]. The RF models in this analysis had higher discrimination: median AUROC up to 0.742 for static RF models and 0.775 for dynamic RF models at landmark 5, compared to 0.721 and 0.747 respectively for regression models. The calibration was similar for RF and regression models: median E:O ratio at LM5 between 0.95 and 0.97 for RF models and between 0.940 and 0.977 for regression models. Lower performance for survival models that censor the competing risks at their time of occurrence was also observed in the companion study, and this finding is in line with the extensive research done on statistical survival models [7].
For static models, different modeling approaches lead to similar model performance in terms of AUROC but different risk predictions in individuals. This is in line with a growing body of research studying the “between model” variability, which refers to differences in individual predictions arising from variations in model types [27] or feature selection choices [28]. We observed that models using all levels of the outcome (multinomial and competing risks) predicted higher risks than the other models, displayed higher AUPRC and slight miscalibration (higher ECI), but did not display considerable differences in AUROC. Despite the miscalibration, the BSS does not penalize these models, as there is gain of predictive performance in the high predicted risks. Zhou et al demonstrate that for low event rate outcomes, AUPRC puts larger weight on the model’s discriminating ability in high risk predictions compared AUROC and conduct a numerical study in which they observe that AUPRC is often correlated with the Brier Score [29]. Li et al. [30] conducted a study to predict cardiovascular disease in the presence of censoring using survival models (accounting for censoring) and ML methods that did not account for censoring. They observed that misspecified models (models that ignored censoring) produced lower, more conservative predicted risks and correctly specified models (not ignoring censoring) produced higher predicted risks while the differences in AUROC were minimal.
Despite extensive functionality in randomforestSRC (unsupervised and supervised learning with various outcome types, multiple split rules, missing data imputation, variable importance metrics, variable selection strategies) which makes it stand out in the software packages space, limitations exist with regards to tuning strategies, out-of-bag sampling and its feasibility for large datasets. The tuning objectives (e.g., logloss, Brier Score) cannot be changed in the default tune function of the package and the subsample size is not a tunable parameter; we have in change opted to tune the hyperparameters using mlrMBO [16] which offers great flexibility. The randomforestSRC package does not offer the possibility of user-defined in-bags and out-of-bags of different sample sizes, which are useful for dynamic and clustered data. Users can opt in turn for cross-validation, a slower procedure compared to tuning based on OOB predictions; we have opted to adjust the in-bags to a minimum size and gain computational efficiency. While this approach is in essence a test leak, its impact was negligible in our specific setting, as confirmed by comparisons with models built using the ranger package, which does not pose the constraint of equal size in-bags. Possibly admissions present both in-bag and out-of-bag could not be identified based on the small number of features included in our models. However, this approach should be carefully evaluated before being used in other contexts, such as a larger feature set, where it may introduce more pronounced bias. Even after applying all documented suggestions for improving computation time for survival and competing risks models [31], running these models on our large dynamic dataset would not have been feasible. Discretizing event times and applying administrative censoring, as explained in the Data and methods section, resulted in split statistics to be calculated over a limited number of horizons of interest and came with significant computational gain. This solution has broader applications; other studies resort to using only binary classification ML models for computational efficiency, even in the presence of censoring [30], which can lead to decreased sample sizes or introduce bias.
The current study has limitations. As a methodological comparison study, we neither recommend a specific model for clinical use nor evaluate the clinical usefulness of the models. We do not account for the correlation between repeated catheter episodes and landmarks within an admission, assuming that after adjusting for landmark and other features, any residual correlation is minimal. Our comparison between the static model and the dynamic model evaluated at LM0 showed that dynamic models generally outperformed static models in overall performance and discrimination, and had similar calibration, suggesting that ignoring this correlation did not negatively impact the predictive performance.
Two important topics remain to be studied further. First, we assume the only outcome of interest is CLABSI event in any of the next 7 days; the undeniable advantage of survival and competing risks models is that they can present the user with predictions for other time horizons in situations where one prediction horizon is of main interest but other horizons might be of secondary interest. Binary models are the fastest to tune, but if we were to build binary models for horizons 1 to 7 (either independent models or built with a monotonicity constraint on predictions), their computational advantage would most probably not persist. Moreover, we are not exploring multiple prediction horizons of interest (7, 14, 30,...) due to the high computational time on our large dataset.
Second, the models that use all levels of the outcome (multinomial and competing risks) display some particularities in tuned hyperparameters, variables used in early tree splits, distribution of predicted risks and slight advantages in some of the performance metrics. The difference in minimal depth for these models is most probably a consequence of optimizing the split statistic over multiple outcome classes. We selected the feature set with CLABSI prediction in mind and we did not explicitly include predictive features for death and discharge. Extensive research would be needed, either using simulated data or real datasets including strong predictors for all outcome levels to understand to which extent the feature selection impacts the model performance when multiple outcome levels are used.
Conclusion
In our studied settings, complex models did not considerably improve the predictive performance compared to a binary model, which can be considered the easiest choice both in terms of model development and in computational time. Importantly, censoring the competing events at their time of occurrence should be avoided in survival models. More research is needed to study the impact of feature selection in models with multiple levels of outcome (multinomial and competing risks).
Supplementary information
Additional file 1: Supplementary materials 1–11.
Acknowledgements
The resources and services used in this work were provided by the VSC (Flemish Supercomputer Center), funded by the Research Foundation - Flanders (FWO) and the Flemish Government.
Abbreviations
- AUPRC
Area under the precision recall curve
- AUROC
Area under the receiver operating characteristic curve
- BS
Brier Score
- BSI
Bloodstream infection
- BSS
Brier Skill Score
- CICC
Centrally inserted central catheters
- CIF
Cumulative incidence functions
- CLABSI
Central line-associated bloodstream infections
- CR
Competing risks
- CRP
C-reactive protein
- CVC
Central venous catheter
- ECI
Estimated Calibration Index
- EHR
Electronic Health Records
- FWO
Research Foundation-Flanders
- ICD
International Classification of Diseases
- ICU
Intensive care unit
- IQR
Interquartile range
- KWS
Klinisch Werkstation (EHR System)
- LC-BSI
Laboratory-confirmed bloodstream infection
- LM
Landmark
- LR
logrank
- LRCR
logrankCR (logrank competing risks)
- LWS
Laboratorium Werkstation (Laboratory System)
- ML
Machine learning
- NMSE
Normalized mean square error
- OOB
Out of bag
- PICC
Peripherally inserted central catheter
- PDMS
Patient Data Management System (ICU Management System)
- RAM
Random access memory
- RF
Random Forest
- TIVAD
Totally implanted vascular access devices
- TPN
Total parenteral nutrition
- VSC
Flemish Supercomputer Center
- WBC
White blood cells count
Authors’ contributions
E.A., S.G., P.S., B.C., and L.W. conceptualized the study. P.S., B.C., and L.W. secured the funding and obtained IRB approvals. P.S. managed data collection. F.R., V.C., Y.D., and C.J. provided clinical inputs. E.A and S.G. performed the data preprocessing and analysis. B.C. and L.W. provided methodological guidance on the modeling framework. E.A. prepared the original draft and all authors participated in revising and editing the article.
Funding
This work was supported by the Internal Funds KU Leuven [grant C24M/20/064]. The funding sources had no role in the conception, design, data collection, analysis, or reporting of this study.
Data availability
The data used in this study cannot be shared publicly due to for the privacy of individuals that participated in the study.
Declarations
Ethics approval and consent to participate
The study was approved by the Ethics Committee Research UZ/KU Leuven (EC Research, https://admin.kuleuven.be/raden/en/ethics-committee-research-uz-kuleuven#) on 19 January 2022 (S60891). The Ethics Committee Research UZ/KU Leuven waived the need to obtain informed consent from participants. All patient identifiers were coded using the pseudo-identifier in the data warehouse by the Management Information Reporting Department of UZ Leuven, according to the General Data Protection Regulation (GDPR).
Consent for publication
Not applicable.
Competing interests
The authors declare that they have no competing interests.
Footnotes
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Moor M, Rieck B, Horn M, Jutzeler CR, Borgward K. Early prediction of sepsis in the ICU using machine learning: a systematic review. Front Med. 2021;8:607952. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Fleuren LM, Klausch TL, Zwager CL, Schoonmade LJ, Guo T, Roggeveen LF, et al. Machine learning for the prediction of sepsis: a systematic review and meta-analysis of diagnostic test accuracy. Intensive Care Med. 2020;46:383–400. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Yan MY, Gustad LT, Nytrø Ø. Sepsis prediction, early detection, and identification using clinical text for machine learning: a systematic review. J Am Med Inform Assoc. 2022;29(3):559–75. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Deng HF, Sun MW, Wang Y, Zeng J, Yuan T, Li T, et al. Evaluating machine learning models for sepsis prediction: A systematic review of methodologies. Iscience. 2022;25(1). [DOI] [PMC free article] [PubMed]
- 5.Frondelius T, Atkova I, Miettunen J, Rello J, Vesty G, Chew HSJ, et al. Early prediction of ventilator-associated pneumonia with machine learning models: A systematic review and meta-analysis of prediction model performance. Eur J Intern Med. 2024;121:76-87. [DOI] [PubMed]
- 6.Hodgson LE, Sarnowski A, Roderick PJ, Dimitrov BD, Venn RM, Forni LG. Systematic review of prognostic prediction models for acute kidney injury (AKI) in general hospital populations. BMJ Open. 2017;7(9):e016591. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Austin PC, Lee DS, Fine JP. Introduction to the analysis of survival data in the presence of competing risks. Circulation. 2016;133(6):601–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Breiman L. Random forests. Mach Learn. 2001;45:5–32. [Google Scholar]
- 9.Ishwaran H, Kogalur UB, Blackstone EH, Lauer MS. Random survival forests. Ann Appl Stat. 2008;2(3):841–60. 10.1214/08-AOAS169. [Google Scholar]
- 10.Ishwaran H, Gerds TA, Kogalur UB, Moore RD, Gange SJ, Lau BM. Random survival forests for competing risks. Biostatistics. 2014;15(4):757–73. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Gao S, Albu E, Tuand K, Cossey V, Rademakers F, Van Calster B, et al. Systematic review finds risk of bias and applicability concerns for models predicting central line-associated bloodstream infection. J Clin Epidemiol. 2023;161:127–39. [DOI] [PubMed] [Google Scholar]
- 12.Duysburgh E. Surveillance bloedstroom infecties in Belgische ziekenhuizen - Protocol 2019. Brussel: Sciensano. 2019. https://www.sciensano.be/sites/default/files/bsi_surv_protocol_nl_april2019.pdf. Accessed 25 Nov 2024.
- 13.Albu E. missForestPredict: Missing Value Imputation using Random Forest for Prediction Settings. 2023. R package version 1.0. https://github.com/sibipx/missForestPredict. Accessed 25 Nov 2024.
- 14.Ishwaran H, Kogalur UB, Kogalur MUB. Package ‘randomForestSRC’. Breast. 2023;6(1):854. [Google Scholar]
- 15.Probst P, Wright MN, Boulesteix AL. Hyperparameters and tuning strategies for random forest. Wiley Interdiscip Rev Data Min Knowl Disc. 2019;9(3):e1301. [Google Scholar]
- 16.Bischl B, Richter J, Bossek J, Horn D, Thomas J, Lang M. mlrMBO: A modular framework for model-based optimization of expensive black-box functions. 2017. https://arxiv.org/abs/1703.03373. Accessed 25 Nov 2024.
- 17.Ishwaran H, Chen X, Minn AJ, Lu M, Lauer MS, Kogalur UB. randomForestSRC: minimal depth vignette. 2021. https://www.randomforestsrc.org/articles/minidep.html. Accessed 25 Nov 2024.
- 18.van Houwelingen H, Putter H. Dynamic prediction in clinical survival analysis. Boca Raton: CRC Press; 2011.
- 19.Ishwaran H, Gerds TA, Lau BM, Lu M, Kogalur UB. randomForestSRC: Competing Risks Vignette. Online vignette. 2021. https://www.randomforestsrc.org/articles/competing.html. Accessed 25 Nov 2024.
- 20.Lau B, Cole SR, Gange SJ. Competing risk regression models for epidemiologic data. Am J Epidemiol. 2009;170(2):244–56. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Van Calster B, McLernon DJ, Van Smeden M, Wynants L, Steyerberg EW, Topic Group ‘Evaluating diagnostic tests and prediction models’, et al. Calibration: the Achilles heel of predictive analytics. BMC Med. 2019;17:1–7. [DOI] [PMC free article] [PubMed]
- 22.Van Hoorde K, Van Huffel S, Timmerman D, Bourne T, Van Calster B. A spline-based tool to assess and visualize the calibration of multiclass risk predictions. J Biomed Inform. 2015;54:283–93. [DOI] [PubMed] [Google Scholar]
- 23.Goldstein BA, Navar AM, Pencina MJ, Ioannidis JP. Opportunities and challenges in developing risk prediction models with electronic health records data: a systematic review. J Am Med Inform Assoc JAMIA. 2017;24(1):198. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Fine JP, Gray RJ. A proportional hazards model for the subdistribution of a competing risk. J Am Stat Assoc. 1999;94(446):496–509. [Google Scholar]
- 25.Wright MN, Ziegler A. “ranger: A Fast Implementation of Random Forests for High Dimensional Data in C++ and R.” J Stat Softw. 2017;77:1–17.
- 26.Gao S, Albu E, Putter H, Stijnen P, Rademakers F, Cossey V, et al. A comparison of regression models for static and dynamic prediction of a prognostic outcome during admission in electronic health care records. 2024. arXiv preprint arXiv:240501986.
- 27.Ledger A, Ceusters J, Valentin L, Testa A, Van Holsbeke C, Franchi D, et al. Multiclass risk models for ovarian malignancy: an illustration of prediction uncertainty due to the choice of algorithm. BMC Med Res Methodol. 2023;23(1):276. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Pate A, Emsley R, Ashcroft DM, Brown B, Van Staa T. The uncertainty with using risk prediction models for individual decision making: an exemplar cohort study examining the prediction of cardiovascular disease in English primary care. BMC Med. 2019;17:1–16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Zhou QM, Zhe L, Brooke RJ, Hudson MM, Yuan Y. A relationship between the incremental values of area under the ROC curve and of area under the precision-recall curve. Diagn Prognostic Res. 2021;5:13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Li Y, Sperrin M, Ashcroft DM, Van Staa TP. Consistency of variety of machine learning and statistical models in predicting clinical risks of individual patients: longitudinal cohort study using cardiovascular disease as exemplar. BMJ. 2020;371:m3919. [DOI] [PMC free article] [PubMed]
- 31.Ishwaran H, Lu M, Kogalur UB. Speed up random forest analyses. https://www.randomforestsrc.org/articles/speedup.html. Accessed 25 Nov 2024.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Additional file 1: Supplementary materials 1–11.
Data Availability Statement
The data used in this study cannot be shared publicly due to for the privacy of individuals that participated in the study.