Summary
Macromolecular crowding has a profound impact on reaction rates and the physical properties of the cell interior, but the mechanisms that regulate crowding are poorly understood. We developed Genetically Encoded Multimeric nanoparticles (GEMs) to dissect these mechanisms. GEMs are homomultimeric scaffolds fused to a fluorescent protein that self-assemble into bright, stable particles of defined size and shape. By combining tracking of GEMs with genetic and pharmacological approaches, we discovered that the mTORC1 pathway can modulate the effective diffusion coefficient of particles ≥ 20 nm in diameter more than 2-fold by tuning ribosome concentration, without any discernable effect on the motion of molecules ≤ 5 nm. This change in ribosome concentration affected phase separation both in vitro and in vivo. Together, these results establish a role for mTORC1 in controlling both the mesoscale biophysical properties of the cytoplasm and biomolecular condensation.
Introduction
Molecular crowding is crucial for the efficient function of biological systems (Zhou et al., 2008). If Xenopus egg extracts are diluted by more than a few percent, fundamental biological processes such as mitosis and DNA replication fail (Lohka and Maller, 1985). High concentrations of crowding agents entropically favor molecular association events, thereby accelerating molecular reactions (Zhou et al., 2008). However, excessive crowding can also dramatically decrease molecular motion, just as the loss of a lane on a freeway can transform smooth traffic flow to instant gridlock (Miermont et al., 2013; Trappe et al., 2001). The impact of crowding depends strongly on particle size: molecules with sizes equivalent to or larger than the dominant crowding agent will be more affected than small particles. These smaller particles can move more easily through the gaps between crowding particles. Thus, changes in molecular crowding can have profound effects on cell physiology and may affect some pathways disproportionately depending on the sizes of the molecules or complexes involved.
Phase separation is a key example of when the regulation of macromolecular crowding is crucial (Woodruff et al., 2017). Proteins that have a stronger propensity to self-associate than to interact with the solvent can undergo a phase transition, where a large number of interacting proteins coalesce into a condensed liquid phase that is separate from the surrounding bulk liquid solvent (Banani et al., 2016; Brangwynne et al., 2009). These biological condensates are increasingly observed in diverse fields including cell division (Woodruff et al., 2017), development (Brangwynne et al., 2009), cancer (Grabocka and Bar-Sagi, 2016; Kaganovich et al., 2008), neurodegenerative disease (Kwon et al., 2014), T-cell activation (Alberti and Hyman, 2016; Su et al., 2016), and even photosynthesis (Freeman Rosenzweig et al., 2017). Macromolecular crowding tunes phase separation in vitro (Woodruff et al., 2017). However, the physiological mechanisms that control crowding within the cell and the effects of crowding on phase separation in vivo remain obscure.
One method to study macromolecular crowding and other cellular biophysical properties is to observe the motion of tracer particles as they move within the cell. This approach, known as passive microrheology, can be used to infer the viscosity, elasticity, structure, and dynamics of the surrounding material from the characteristic motion of these tracer particles (Wirtz, 2009). Various groups have studied the motion of non-biological nanoparticles in cells (Daniels et al., 2006; Luby-Phelps et al., 1986), but these techniques are labor intensive and typically perturb the cell. For example, microinjection dilutes the cytoplasm, disrupts the cell membrane and cortex, and is not possible in organisms with a cell wall, such as budding yeast. An alternative approach is to track the motion of endogenous structures, such as mRNA molecules tagged with specific loops that interact with loop-binding proteins tagged with fluorescent proteins (Shav-Tal et al., 2004). However, if the motion of an endogenous molecule is affected by a perturbation, it is difficult to know if these changes in motion are due to impacts on the biophysical properties of the cell or caused by direct regulation of the tracer particle.
In order to address these issues, we developed Genetically Encoded Multimeric (GEM) nanoparticles (henceforth GEMs), which are bright tracer particles of a defined shape and size. GEMs can serve as a standard microrheological tool across a broad range of organisms; in this study, we used GEMs in S. cerevisiae and human cell lines. By using GEMs from a different kingdom than the organism of study, we make it far less likely that the particles will be affected by specific interactions. With this technology in hand, we screened for mechanisms that regulate the biophysical properties of cells. We found that the mTORC1 kinase controls ribosome abundance through a combination of cell volume control, ribosome biogenesis and autophagy. In situ cryo-electron tomography (cryo-ET) of the native cellular environment revealed that inhibition of mTORC1 nearly halves the cytosolic ribosome concentration in S. cerevisiae. As ribosomes account for ~20% of the total cytosolic volume, modulation of their concentration has a dramatic effect on the biophysical properties of the cell. This modulation is significant: inhibition of mTORC1 can double the effective diffusion coefficient of particles that are ≥ 20 nm in diameter. Using the phenomenological Doolittle equation, which relates the diffusion of a tracer particle to the fraction of crowding, we were able to predict changes in the effective diffusion coefficient as a function of ribosome concentration in both budding yeast (S. cerevisiae) and human cells (HEK293). Finally, we found that changes in macromolecular crowding downstream of mTORC1 tune phase separation in both yeast and human cells, providing a direct link between in vivo crowding and phase separation.
Results
GEMs can be made from both 15 nm and 35 nm icosahedral protein cages
We developed GEMs to study the rheological properties of the eukaryotic cytoplasm. We began with natural homomultimeric scaffolds that self-assemble into icosahedral geometries and fused these scaffolds to fluorescent proteins (T-Sapphire).
In this study, we employed scaffolding domains based on the encapsulin protein from the hyperthermophilic archaeon Pyrococcus furiosus (Akita et al., 2007) and the lumazine synthase enzyme complex from the hyperthermophilic bacterium Aquifex aeolicus (Zhang et al., 2001) (figure 1A–C). When expressed within cells, these GEMs self-assembled into bright, stable particles (figure 2A–B).
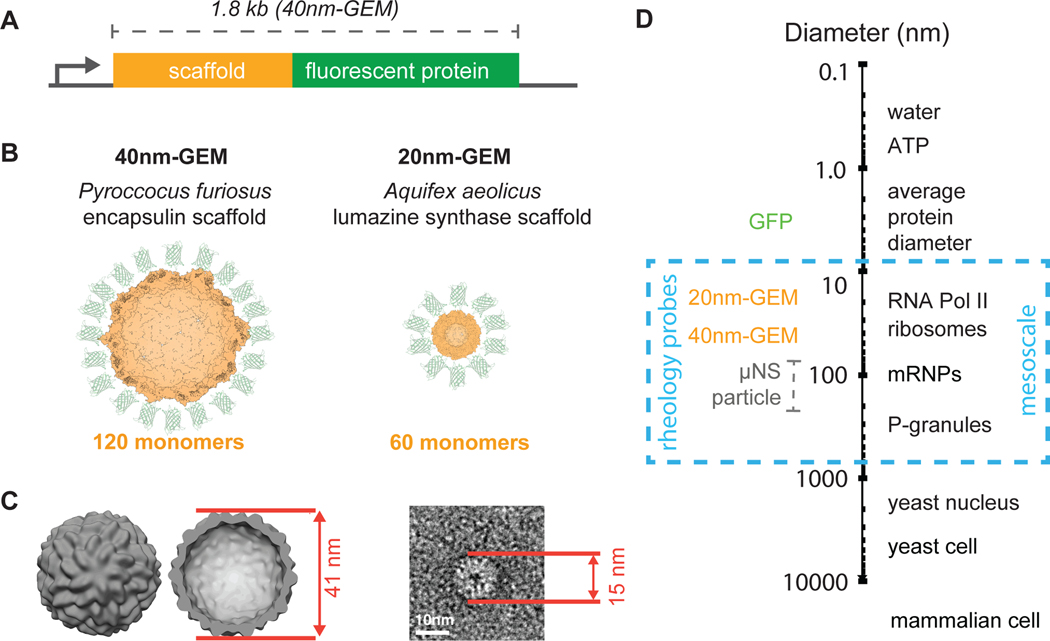
Figure 1. Genetically Encoded Multimeric nanoparticles (GEMs) are homomultimeric fluorescent nanoparticles that self-assemble to a stereotyped size and shape.
(A) General gene structure of GEMs, which consist of an in-frame fusion of a multimerizing scaffold (orange) to a fluorescent protein (green). (B) Predicted structures of 40nm-GEMs and 20nm-GEMs. (C) Left, cryo-ET subtomogram average of 40nm-GEMs within the cell; Right, negative stain EM image of a 20nm-GEM. Diameters are shown in red. (D) Diameters of GEMs and other macromolecules at the meso length-scale, shown in relation to small molecules, protein complexes, and cells.
Figure 2. mTORC1 inhibition increases the effective diffusion coefficient of GEMs.
(A) 40nm-GEMs expressed in (A) S. cerevisiae and (B) HEK293 cells. GEMs are visualized using the T-Sapphire fluorescent protein (green). The SiR-Hoeschst DNA stain is used to visualize the nucleus (Nuc, magenta). Yeast cell walls are visualized using calcofluor-white and HEK293 membrane with wheat germ agglutinin (cyan). (C) High magnification example of tracking a 40nm-GEM particle (green) within a S. cerevisiae cell, imaged at 100 frames per second. Three other GEMs and the nucleus (magenta) are also seen within the image. Raw pixels are displayed. (D-E) Distribution of 40nm-GEM effective diffusion coefficients (Deff) within S. cerevisiae (D) and HEK293 cells (E); results from DMSO (carrier control) treatment and rapamycin treatment are displayed in blue and orange, respectively. Insets: time and ensemble-averaged mean-square displacements in log-log space with the anomalous exponent indicated. (F) Cumulative distribution function showing Deff data for both S. cerevisiae (solid lines) and HEK293 cells (dashed lines) in both control (blue) and rapamycin treatment (orange).
Using in situ cryo-ET to image the native cellular environment (Asano et al., 2016), we determined that the Pyrococcus furiosus encapuslin GEM has a diameter of 41 nm, a little larger than the 35 nm diameter reported from crystallography data (figure 1C). This larger diameter is likely due to the additional T-Sapphire molecules decorating the encapsulin particle. Thus, we termed these particles 40nm-GEMs.
Using negative stain electron microscopy, we measured a diameter of 15 nm for the A. aeolicus lumazine synthase GEM (figures 1C and S1A), in good agreement with crystallography data (Zhang et al., 2001) (figure 1C). However, it is likely that the T-Sapphire density was not visible in the negative stain images (see also figure S1B, where Pyrococcus furiosus encapuslin GEMs were measured at 37 nm by negative stain). Thus, to account for the expected extra diameter due to decoration with GFP molecules, we termed these particles 20nm-GEMs.
The 20nm-GEMs and 40nm-GEMs are in the size range of multi-subunit assemblies such as ribosomes, proteasomes and chromatin remodeling complexes (figure 1D), allowing us to investigate the mesoscale microrheological environment experienced by these complexes. Thus, these biologically-orthogonal nanoparticles probe the biophysical properties of the cell at a length-scale that was previously challenging to study.
GEMs allow rapid characterization of the rheological properties of the cytosol in yeast and human cells
We expressed 40nm-GEMs in the budding yeast S. cerevisiae and an adenovirus transformed Human Embryonic Kidney cell line (HEK293) (figure 2A–B, supplemental movies 1–2). 40nm-GEMs are bright enough to allow single particle tracking at 10 ms frame rates (figure 2C, see methods). The duration of tracking is limited to the amount of time a particle remains in a single focal plane, as the required acquisition rate did not permit the collection of z-stacks, thus the median track length was 35 frames, corresponding to 350 ms of imaging (figure S1C). We compared thousands of individual traces to extract the effective coefficient of diffusion, Deff, at short timescales (100 ms). GEM motion differs between the two biological systems: 40nm-GEMs have a median effective diffusion coefficient of ~ 0.3 μm2 s−1 in yeast and ~ 0.5 μm2 s−1 in mammalian cells (figure 2D–E). These estimates are in good agreement with expectations from the literature (Luby-Phelps et al., 1986), further supporting the use of GEMs as microrheological standards. Using time and ensemble-averaging, we inspected the mean-squared displacement (MSD) curves at longer timescales and found that 40nm-GEMs were subdiffusive (inset figure 2D–E, S2A) with an anomalous exponent of ~ 0.8 in yeast and ~ 0.9 in HEK293 cells. This subdiffusive motion could be due to local caging within a crowded environment and/or interactions between the tracer particle and the environment (Wang et al., 2012). However, the anomalous exponent did not change significantly in most of our perturbation experiments (figure S2A), so we focused on the effective diffusion coefficient as our main metric to report on cytosolic rheology at the mesoscale.
mTORC1 affects the biophysical properties of the cytosol
In initial experiments in yeast, we observed that cell culture conditions changed the apparent diffusion coefficients of 40nm-GEMs. When yeast cultures approached saturation, the effective diffusion of GEMs increased (figure S2B). By specifically depleting nitrogen, glucose, and amino acids, the main components of synthetic complete growth medium, we found that both nitrogen and glucose starvation caused a slight decrease in the apparent diffusion of 40nm-GEMs, but this decrease was subtle compared to previous reports with larger particles (Joyner et al., 2016; Munder et al., 2016a) (figure S2D). In contrast, we found that an increase in effective diffusion occurred in response to amino acid depletion (figure S2C).
The mechanistic target of rapamycin complex (mTORC1) is the major amino acid sensor in eukaryotes (Hara et al., 1998). Therefore, we hypothesized that mTORC1 signaling might cause the observed changes in cytoplasmic rheology. mTORC1 can be inhibited by rapamycin, Consistent with our hypothesis, 40nm-GEMs displayed increased mobility upon addition of rapamycin in both S. cerevisiae and HEK293 cells (figure 2D–E, supplemental movies 1–2). This increase in effective diffusion reached full effect after 2 and 3 hours of rapamycin treatment in yeast and HEK293 cells, respectively (figure S2D–E). Changes in the distribution of diffusion coefficients were highly significant (p < 1 × 10−9; Kolmogorov-Smirnov test, figure 2F). Importantly, in situ cryo-electron tomography (cryo-ET) showed that 40nm-GEMs did not change size after rapamycin treatment (figure S3). These results suggest that mTORC1 controls the biophysical properties of the cytosol at the 40 nm length-scale in both yeast and mammalian cells.
mTORC1 does not affect diffusion at the length-scale of individual proteins
The change in effective diffusion of 40nm-GEMs was clear, but cellular rheology can vary considerably between particles of different sizes. Therefore, we studied other particles to check the generality and length-scale dependence of the changes in microrheology downstream of mTORC1 signaling. First, we repeated our experiments with 20nm-GEMs and found that their diffusion also increased upon mTORC1 inhibition (figure 3A). We also saw an increase in the diffusion coefficients of larger structures, including endogenous GFA1 mRNP tagged with the PP7-GFP system (Joyner et al., 2016) and GFP-μNS particles (figure 3B–C). These structures are approximately 100 nm and 200 nm in diameter, respectively. Thus, mTORC1 modulates the effective diffusion coefficient of particles in the mesoscale, ranging from 20 nm to 200 nm in diameter.
Figure 3. mTORC1 inhibition increases the effective diffusion of particles 20 nm and larger in S. cerevisiae.
(A-C) Cumulative distribution plots showing Deff data for 20nm-GEMs (A), GFA1 mRNP particles (B), and μNS condensates (C) in yeast cells treated with DMSO (blue) or rapamycin (orange). (D) Fluorescence correlation spectroscopy (FCS) autocorrelation function for a tandem GFP dimer (Stokes radius of ~ 5 nm). There is no significant difference between DMSO and rapamycin. (E) Effect of rapamycin on the effective diffusion coefficients of endogenous molecules and tracer particles of various sizes. Indicated, the −2 power-law scaling of diffusion coefficient as a function of diameter, which does not conform to Stokes-Einstein predictions. In all cases control conditions are shown in blue and rapamycin in orange.
To probe rheology at shorter length-scales, we used fluorescence correlation spectroscopy to calculate the effective diffusion of a double-GFP molecule, which has a hydrodynamic radius of around 5 nm. The diffusion of this smaller protein was unaffected by the addition of rapamycin (figure 3D, table S1). Thus, mTORC1 inhibition increases the diffusion coefficients of particles at or above the typical size of multimeric protein complexes, but particles that are the typical size of monomeric proteins are unaffected (figure 3E).
Changes in cell cycle, translation and the cytoskeleton do not account for the effects of mTORC1 on the motion of 40nm-GEMs
Rapamycin treatment arrests cells in the G1 phase of the cell cycle. Therefore, we hypothesized that the increase in the effective diffusion coefficients of 40nm-GEMs might be due to cell cycle regulation of rheology. To test this idea, we inhibited the cdc28-as1 allele of budding yeast Cyclin Dependent Kinase 1 (Cdk1) with 10 μM 1-NM-PP1 (Bishop et al., 2000). Cell division arrested in G1 and cell volume continued to increase, but no changes were observed in the motion of 40nm-GEMs (figure S2F–G). Thus, cell cycle regulation does not appear to explain the observed biophysical effects of mTORC1 inhibition.
Protein translation is regulated by mTORC1: when nutrients and growth factors are present, cells enter an anabolic state and protein translation is upregulated in an mTORC1-dependent manner. Inhibition of mTORC1 with rapamycin leads to rapid inhibition of translation. Therefore, we tested whether decreases in translation could explain the observed changes in the effective diffusion coefficients of 40nm-GEMs. To investigate this idea, we stalled translation by addition of 1 μM cycloheximide. The median half-life of yeast proteins is ~ 40 minutes under these conditions (Belle et al., 2006). The motion of 40nm-GEMs was neither affected during acute cycloheximide treatment, nor after 180 minutes of treatment (figure S2F). These results suggest that neither translational inhibition nor protein degradation explain our observations.
Another plausible hypothesis is that mTORC1 might alter the dynamics or structure of the cytoskeleton. We treated yeast cells with Latrunculin A to depolymerize the actin cytoskeleton (figure S2H) and found that, while the basal diffusion of 40nm-GEMs decreased, there was still a strong increase in Deff upon rapamycin treatment. We also arrested actin dynamics in HEK293 cells using the JLY cocktail (Peng et al., 2011) (figure S2F). Similar to yeast, perturbation of actin dynamics decreased basal GEM diffusion, but rapamycin still had a strong effect (figure S2H). These results suggest that the actin cytoskeleton contributes substantially to the viscosity of both the mammalian and yeast cytoplasm, but that mTORC1 does not modulate mesoscale rheology through actin-dependent effects. We then used nocodazole to depolymerize microtubules. There was a slight decrease in viscosity in both yeast and mammalian cells, but there was not a strong effect on the relative effect of rapamycin (figure S2G, H). Thus, actin and microtubules play an important role in defining the mesoscale properties of the cytosol, but do not appear to be the primary mechanistic explanation for the regulation of rheology by mTORC1.
mTORC1 controls cytoplasmic rheology by tuning ribosome concentration
In our S. cerevisiae experiments, we could collect thousands of traces within a few seconds. Because every cell expressed GEMs, there was no time delay associated with finding cells, and no laborious manipulations like microinjection. These advantages enabled us to use GEMs in a candidate based genetic screen (table S2). In the absence of the FPR1 gene (encoding FKBP12), rapamycin cannot inhibit mTORC1 (Heitman et al., 1991). There was no detectable effect of rapamycin on the fpr1Δ strain (figure 4A), indicating that rapamycin was affecting rheology by a canonical mechanism. SIT4 encodes a subunit of the PP2A phosphatase required for a major signaling branch downstream of mTORC1 (Di Como and Arndt, 1996). Addition of rapamycin to sit4Δ cells had little to no effect on particle diffusion suggesting that the change in physical properties of the cytoplasm were downstream of this gene. Together, these results validated the use of 40nm-GEMs in genetic screens and constrained our genetic screen to the PP2A-dependent branch of mTORC1-signaling.
Figure 4. mTORC1 controls the effective diffusion coefficient of 40nm-GEMs by tuning ribosome concentration.
(A) Selected mutants from a candidate screen in S. cerevisiae. The change in the baseline effective diffusion coefficients of 40nm-GEMs (left, blue) is plotted for each mutant, along with the magnitude of the rapamycin effect normalized to the effect in wild-type cells (ε right, orange; 0 = no rapamycin effect, 1 = same effect as wild-type). (B) Pharmacological and siRNA perturbations in HEK293 cells suggest that mTORC1 also modulates cytoplasmic rheology through ribosome crowding in mammals. Data are presented as the median +/− SEM (standard error of the mean). (C) Proposed model of crowding control in S. cerevisiae and HEK293 cells.
We tested and rejected several hypotheses for the possible mechanism through which mTORC1 signaling might affect cytosolic biophysics (table S2). Eventually, we found that deletion of the SFP1 gene, which encodes a transcription factor involved in ribosomal RNA biogenesis (Fingerman et al., 2003), increased the effective diffusion coefficient of 40nm-GEMs even more than rapamycin treatment (figure 4A, left). Furthermore, the sfp1Δ strain led to a complete loss of the rapamycin effect (figure 4A, right). The results implicated ribosome biogenesis as a key mechanism in the control of cellular rheology.
Ribosomes are usually quite stable, but starvation conditions can drive autophagy and ribophagy to accelerate ribosome degradation, especially when mTORC1 is inhibited (Waliullah et al., 2017). This starvation response is thought to scavenge macromolecules and organelles to recycle cellular building blocks, but reduction in the concentration of ribosomes has also been proposed as a function for these pathways (Tsukada and Ohsumi, 1993). In accordance with this latter idea, mutations in the autophagy genes ATG1, ATG13 and ATG17 and the ribophagy gene RIM15 (Waliullah et al., 2017) all caused a significant abrogation of the rapamycin effect (figure 4A, right).
Next, we sought to determine whether the mechanisms that we identified in S. cerevisiae would also hold true in mammalian cells. To this end, we employed HEK293 cells stably transduced or transfected with 40nm-GEMs and used pharmacological perturbations and siRNA to test whether ribosome concentration was important in setting the biophysical properties of mammalian cells at the 40 nm length-scale.
Inhibition of ribosome production using the small molecules BMH-21 or CX5461 reduced the rapamycin effect (figure 4B, right). However, the basal diffusion coefficient only increased in CX5461 treatment (figure 4B, left). We speculate that the failure of BMH-21 to impact GEM motion could be due to off-target effects of this drug, which could lead to compensatory effects in the basal biophysical properties of the cytoplasm. Nevertheless, these pharmacological perturbations suggest that control of rDNA transcription is part of the mechanism by which mTORC1 inhibition decreases the viscosity of mammalian cells.
Stimulation of autophagy using the SMER28 compound, thereby reducing ribosome concentration, led to an increase in the basal diffusion of 40nm-GEMs (figure 4B, left) and strongly suppressed the effect of rapamycin (figure 4B, right). In contrast, decreasing autophagy with Wortmanin, which is predicted to increase ribosome concentration, led to decreased basal diffusion (figure 4B, left). This perturbation also led to a partial loss of the rapamycin effect (figure 4B, right).
Finally, we increased mTORC1 activity by siRNA-mediated knockdown of the mTORC1 inhibitor TSC1 (Potter et al., 2001). This treatment led to a decrease in basal diffusion (figure 4B, left, S2J). Thus, after screening over 40 mutants and drug treatments, we found that the conditions that most strongly affected the baseline of GEM diffusion and/or decreased the effect of rapamycin treatment fell into two general classes: ribosome biogenesis and autophagy. Together, these data suggest that mTORC1 controls macromolecular crowding by tuning ribosome concentration (figure 4C).
Ribosomes act as crowding agents
To test further investigate the control of ribosome concentration by mTORC1, we used in situ cryo-ET to directly visualize ribosomes. Briefly, we thinned vitreous frozen yeast cells by focused ion beam (FIB) milling (Schaffer et al., 2017) and then performed in situ cryo-ET (Albert et al., 2017; Bykov et al., 2017; Guo et al., 2018) to produce three-dimensional images of the native cellular environment at molecular resolution (figures 5A–B, S3–S6, supplemental movies 3–4). Template matching enabled us identify ribosomes within the cellular volumes with high sensitivity (figure S4). Subsequent subtomogram averaging produced in situ structures of the ~30 nm ribosomes and 40nm-GEMs at 11.5 Å and 26.3 Å resolutions, respectively (figures 5C, S3–S4). In W303 yeast cells undergoing log phase growth, the concentration of ribosomes in the cytoplasm was ~14,000 ribosomes/μm3 (23 μM), whereas this concentration decreased almost 2-fold to ~8,000 ribosomes/μm3 (13 μM) when cells were treated with rapamycin for two hours (figure 5D). This corresponds to a drop from ribosomes occupying ~ 20% to ~ 12% of the cytosolic volume.
Figure 5. In situ cryo-electron tomography of FIB-milled S. cerevisiae reveals that ribosome concentration dramatically decreases upon mTORC1 inhibition.

(A) DMSO-treated cell. (B) Rapamycin-treated cell. (Left) Slice through a representative cryo-electron tomogram of a FIB-milled yeast cell. The cell wall (CW), plasma membrane (PM), rough endoplasmic reticulum (rER), lipid droplets (LD), mitochondria (M), Golgi apparatus (G), vacuole (V), aggregates (Agg), and one example GEM nanoparticle are indicated. (Right) 3D segmentation of the same tomogram showing ribosomes (cyan) and GEMs (orange). The non-cytosolic volume is grey. (C) Subtomogram averages of the 40nm-GEM nanoparticles and ~30 nm ribosomes from within the cellular volumes, shown in relative proportion. (D) Cytosolic ribosome concentrations after 2 h DMSO (blue) and rapamycin (orange) treatment. Error bars are SEM. Concentrations were calculated from 14 DMSO-treated and 13 rapamycin-treated cells (see figures S5 and S6).
Ribosomes control the biophysical properties of the cytosol
To further investigate how ribosome concentration controls the mesoscale viscosity of the cytosol, we developed a physical model, based on the phenomenological Doolittle equation (Doolittle, 1952) see methods, equation 5). Originally, the Doolittle equation was used to describe the viscosity of liquid polymer melts as a function of polymer density (i.e., polymer crowding). Later, Cohen and Turnbull derived the equation theoretically to describe the viscosity of hard-sphere colloids (Cohen and Turnbull, 1959). Thus, the equation has been successfully used to fit the viscosity of a range of materials (Hunter and Weeks, 2012). The Doolittle equation relates crowding to diffusion using an exponential function of the concentration of crowder () divided by the maximum possible crowding () and a prefactor related to the strength of interaction of the tracer particle with its surrounding microenvironment (equation 5 and figure 6A.)
Figure 6. A physical model of the cytosol accurately predicts diffusion as a function of ribosome concentration.
(A) The phenomenological Doolittle equation describes the effective diffusion coefficient of particles as a function of excluded volume, the volume of the cytoplasm occupied by macromolecules. (B and C) A model based on the Doolittle equation to relate Deff to the concentration of ribosomes, , parameterized empirically with no parameter fitting, accurately predicts the diffusion coefficient of 40nm-GEMs in both yeast (B) and HEK293 cells (C) as a function of the concentration of ribosomes (measured by quantification of a total extracted nucleic acids, see figure S8E-G). Median coefficients of diffusion are normalized to wild-type conditions on the day the data was acquired and plotted as the median +/− SEM. Prediction is shown as a dashed black line with grey confidence intervals based on the error associated with the estimation of and.
To determine the degree of crowding in the cytoplasm under normal conditions (), we manipulated crowding by rapidly changing cell volume through osmotic shock and measured the apparent diffusion coefficient (see figure S7 A–B). We found that is smaller for HEK293 cells (0.35 +/− 0.13) than for S. cerevisiae (0.48 +/− 0.04), confirming our expectation that HEK293 cells are less crowded than yeast. Note that this ratio means that the cytoplasm of a cell is not close to a glass transition, where would be ~ 1. The parameter z is roughly equivalent in both species, perhaps suggesting that 40nm-GEMs have similar interactions with the human and yeast cytosol, a result most easily explained by GEMs having very little specific interaction with their local environment. This concordance further supports the use of GEMs as a microrheological standard across organisms.
Once we had determined the parameters and we were able to predict the effective diffusion coefficient of GEMs as a function of ribosome concentration (see methods, equation 12). All parameters were experimentally determined with no data fitting. We compared our prediction to experimentally determined ribosome concentrations (figures 5, S7D–F. Our model was able to predict the effective diffusion coefficient of GEMs for all mutants and perturbations over a wide range of ribosome concentrations in both yeast and mammalian cells.
We also experimentally determined the prefactor for the endogenous GFA1 messenger ribonucleoprotein complex (mRNP) tagged with the PP7-GFP system. These particles are approximately 100 nm in diameter. Our model accurately predicted their effective diffusion coefficient as a function of ribosome concentration (figure S7C). Therefore, our results suggest that ribosome concentration is a crucial determinant of the mesoscale biophysical properties of the cytosol.
mTORC1 tunes phase separation by controlling ribosome concentration
When multivalent proteins exceed a critical nucleation concentration they can condense to form a phase separated liquid droplet. Phase separation is tuned by multiple physicochemical effects including the association and dissociation constants of interaction domains, the strength of the interaction of each molecule with the solvent, and depletion attraction effects that can entropically favor condensation (Mourão et al., 2014), or linker solvation effects (Harmon et al., 2017). These two latter effects depend on macromolecular crowding. Since our results strongly linked ribosomes to cytoplasmic crowding, we hypothesized that ribosome concentration tunes phase separation. To test this idea, we took advantage of a synthetic system that forms liquid droplets both in vitro and in vivo. This system is comprised of ten repeats of the small ubiquitin-like modifier domain (SUMO10) and six repeats of SUMO interaction motif (SIM6). The condensation of SUMO10 and SIM6 has been proven to be a reliable model for phase separation (Banani et al., 2016).
We assessed the effects of ribosomes on the phase separation of SUMO10 and SIM6. Beginning in vitro, we added ribosomes purified from Escherichia coli over a biologically-relevant concentration range determined from our cryo-ET experiments. We observed that the concentration of SUMO10 and SIM6 that partitioned into the condensed liquid droplet phase (partition coefficient) increased as ribosome concentrations increased. Indeed, the partition coefficient was > 50% higher at 23 μM ribosomes (the in vivo concentration in normal conditions) than at 13 μM (the in vivo concentrations after rapamycin treatment) (figure 7A).
Figure 7. Ribosomes act as a crowding agent that drives phase separation both in vitro and in vivo.
(A) A homodecamer repeat of SUMO (SUMO10) was mixed with a homohexamer repeat SUMO interaction motif peptide (SIM6) to achieve equimolar concentrations of each monomer (60 μM). SUMO10 + SIM6 was kept at constant concentration and incubated with an increasing concentration of fully assembled 70S ribosomes (purified from E. coli). There was a >50% increase in the partition coefficient of SUMO10 + SIM6 when ribosome concentration was increased from 13 μM (equivalent to yeast treated with rapamycin) to 23 μM (the concentration of ribosomes in logarithmically growing yeast cells). (B) An in-frame fusion of SUMO10-SIM6-GFP was expressed in budding yeast (S. cerevisiae W303) and HEK293 cells. Micrographs of control cells (DMSO) and cells treated with rapamycin for 2 h. (C) Quantification of total area of phase-separated droplets in control cells (blue), cells treated with rapamycin (orange), and cells treated with rapamycin followed with a hyperosmotic shock with 1.5M (yeast cells) or 0.1M (human cells) sorbitol (orange bars with white cross hatches). (D) Probability of observing SUMO10-SIM6 phase separation versus ribosome concentration in yeast ribosomal crowding mutants sfp1Δ, rim15Δ, and atg13Δ as well as wild-type BY4741.
Next, we expressed an in-frame fusion of SUMO10 and SIM6 (SUMO10-SIM6) in yeast and HEK293 cells to study the effects of macromolecular crowding on phase separation in vivo. Inhibition of mTORC1 for two hours led to an 80% and 50% decrease in SUMO10-SIM6 droplet area in yeast and human HEK293 cells, respectively (figure 7B). We were able to partially recover phase separation in rapamycin-treated cells by using an acute osmotic shock that reduced cell volume to an extent that restored ribosome concentrations to control levels (figure 7C, orange cross-hatched bars). The degree of phase separation is not completely recovered by osmotic compression, perhaps because this process cannot reach steady state before cells adapt, or because mTORC1 inhibition has effects in addition to crowding.
To avoid unknown effects that rapamycin may have in parallel to changes in ribosome concentration, we used the yeast deletion strains that we had previously determined to affect molecular crowding. For each mutant we quantified ribosome concentration, the total concentration of SUMO10-SIM6 and the probability of finding a SUMO10-SIM6 droplet in a cell. Interestingly, we found very little correlation between phase separation and the concentration of SUMO10-SIM6. We also saw little correlation between SUMO10-SIM6 concentration and ribosome concentration (figure S7G–H). In contrast, there was a strong correlation (r2 = 0.96) between droplet probability and ribosome concentration in this analysis (figure 7D). Taken together, these data suggest that ribosomes act as macromolecular crowders that tune phase separation.
Discussion
Recent work has reported dramatic changes in cytoplasmic rheology in response to changes in cellular energy state and metabolism. For example, depletion of ATP in E. coli leads to a glass transition that greatly reduces macromolecular mobility (Parry et al., 2014), and glucose starvation in yeast leads to decreases in cytoplasmic pH that lead to a gel transition in the cytosol (Munder et al., 2016b). All of these responses increase the viscosity of the cytosol. In contrast, we show that inhibition of mTORC1 decreases cytosolic viscosity. Using GEM nanoparticles, we were able to determine the mechanism for this biophysical change. Ribosome concentration dominates the rheological properties of the cytoplasm at the mesoscale of tens to hundreds of nanometers. mTORC1 both drives ribosome biogenesis and decreases degradation through inhibition of autophagy (Zoncu et al., 2011). Therefore, mTORC1 regulates the physical properties of the cytoplasm by tuning the concentration of ribosomes.
Length-scale considerations in cytoplasmic viscosity have interesting implications for previous findings; for example, solidification of the yeast cytoplasm under glucose starvation was observed by tracking GFP-μNS particles, which are large condensates (Munder et al., 2016a). However, it would be surprising if the diffusion of all macromolecules is greatly decreased in carbon starvation. Our results show that the mobility of 40nm-GEMs is only decreased by 20% in this condition (figure S2B). This result is in agreement with the particle size dependency observed in the bacterial cytoplasm (Parry et al, 2014). In some scenarios, larger macromolecules may become spatially confined while smaller macromolecules continue to diffuse unimpeded. This could affect processes dependent on large complexes, such as apoptosis, translation or cell growth, while many basic cellular functions continue unaltered. In this way, general changes in cytoplasmic crowding could cause specific physiological consequences.
A major advantage of GEM nanoparticles is that they assemble into defined geometries and can therefore be used as rheological probes across multiple biological systems. We observe that GEMs have a higher diffusion coefficient in HEK293 cells than in S. cerevisiae, indicating that this human cell line is less crowded. Indeed, our osmotic compression experiments show a larger free water volume in HEK293 cells, consistent with this notion. In future studies, it will also be interesting to compare the physical properties of mammalian cells in different mechanical contexts, for example within tissues. Additionally, different cell types are likely to have distinct crowding, and disease mutations may lead to aberrant properties. GEMs will be a crucial tool to accelerate discovery in this area.
Beyond the diffusion coefficient, a second parameter that can be readily compared across conditions is the subdiffusive anomalous exponent,. GEMs undergo subdiffusive motion in both cell types, but the origins of this subdiffusion remain unclear. A striking feature is that is relatively invariant across conditions within one cell-type, but there is a species-dependent difference between yeast and human cells (figure S2I). This difference in a points to a general difference within the disordered media of the cytoplasm in these two organisms. While the physical explanation for this difference is currently unknown, there are several possibilities. Notably, mammalian cells have intermediate filaments and far more extensive actin and microtubule networks. This more elaborate cytoskeleton drives more substantial active flows and rearrangements, all of which can affect cytosolic rheology. We are excited to investigate these possibilities in the future.
Ribosomes are one of the most abundant macromolecules in the cell (around 200,000 ribosomes per yeast cell (Warner, 1999) and 3,000,000 per HeLa cell (Duncan and Hershey, 1983)), and we determined that ribosomes occupy 20% of the total volume of the yeast cytosol. Under normal conditions, the fraction of crowder in the cytoplasm is about 50% of the maximum possible crowding (Miermont et al., 2013), thus ribosomes account for about half of this excluded volume. Indeed, when we use the phenomenological Doolittle equation to model the cytosol, we can predict the diffusion coefficient of 40nm-GEM tracer particles and endogenous mRNPs as a function of ribosome concentration. This predictive power suggests that ribosomes are crucial to set the biophysical properties of the cytosol. However, the cytoplasm is unlikely to be well described by a purely colloidal model. This point is indicated by the scaling of diffusion coefficients as a function of particle size (figure 3E). Recent theories provide predictions for particle diffusion within polymer meshes (Cai et al., 2011). In this framework, the diffusion coefficient (D) of tracer particles of a diameter comparable to the mesh size should scale with particle diameter (d) as D ~ d−3. On the other hand, a simple Newtonian fluid or a dilute colloidal suspension predicts D ~ d−1. In our case, we find a scaling of D ~ d−2 indicating that the cytoplasm neither satisfies the model of a simple polymer nor a simple Newtonian fluid. Thus, the biophysical properties of the cytoplasm are likely to be driven by a mixture of the colloidal effects of ribosomes as well as polymer dynamics. Our model provides a starting point to begin to parse the relative contribution of these possible factors, for example from the cytoskeleton or polysomes.
Physiological regulation of the thousands to tens of thousands of different proteins found within cells is a complex task. This regulation is achieved through fine-grained mechanisms, including transcriptional and translational control of protein abundance as well as post-translational modifications such as protein phosphorylation and ubiquitylation. However, our studies suggest that macromolecular crowding could also lead to a broad regulation of cell state. Changes in macromolecular crowding may provide coarse-grained regulation of protein interactions, diffusion and folding; the cell may become more solid-like in states of extreme stress or fluidize to tune reactions.
It has long been understood that molecular crowding is crucial for biological systems. Our work begins to elucidate why. We show that changes in ribosomal crowding tune phase separation both in vitro and in vivo. The effects on phase separation in our system could be attributed to several possible causes including attraction depletion effects (Woodruff et al., 2015) and solvation impacts on the linkers in polyvalent proteins (Harmon et al., 2017). Regardless of mechanism, our finding implies that mTORC1, and indeed any signaling pathway that alters the steady-state concentration of ribosomes, is likely to affect the phase separation of many molecules. Thus, our work provides insights relevant to the burgeoning field of phase separation of cytosolic biomolecular condensates. Interest in this topic is rapidly growing, as investigators elucidate the impacts of phase separation on proteins involved in many fundamental processes such as photosynthesis (Freeman Rosenzweig et al., 2017), cell division (Woodruff et al., 2017), development (Brangwynne et al., 2009), learning (Si et al., 2010), immune signaling (Cai et al., 2014; Hou et al., 2011), and human pathologies including cancer (Kwon et al., 2013), aging and neurodegeneration (Jain and Vale, 2017; Kwon et al., 2014).
STAR Methods
Contact for reagent and resource sharing
Requests for materials should be addressed to the lead contact, Liam Holt (liam.holt@nyumc.org).
Experimental Model and Subject Details
Yeast
Saccharomyces cerevisiae BY4741 and W303 strains were used in this study as indicated in table S2. Strains were grown in synthetic complete media + 2% dextrose (SCD) according to standard Cold Spring Harbor Protocols unless otherwise stated. Exponentially growing cultures between O.D. ≥ 0.1 and ≤ 0.4 were used in all experiments unless otherwise noted. Note: It is extremely important to avoid culture saturation - all cultures were started from single colonies and grown overnight to log phase (typically we set up 1/5 serial dilutions to catch one culture at the correct OD). If cultures saturate, it takes many generations to reset the cellular rheology. All strains were grown at 30 °C in a rotating incubator.
HEK293 Cells
Mammalian cells were maintained at 37 °C with 5% CO2. HEK293 and HEK293T were grown in high glucose DMEM (Life Technologies) supplemented with 10 % fetal bovine serum (FBS; Gemini Bio-products), penicillin (50 U/mL) and streptomycin (0.05 mg/mL) (Life Technologies) unless otherwise stated. HEK293 cell lines are female with AMEL marker X,X. Cell lines were verified using short tandem repeat DNA profiling (STR profiling) by PCR amplification of 9 STR loci plus Amelogeninusing Promega GenePrint 10 System, Fragment Analysis with ABI 3730XL DNA Analyzer, comprehensive data analysis with ABI Genemapper software and final verification using supplier databases including ATCC and DSMZ.
Method Details
Plasmid construction
The open reading frames encoding the Pyrococcus furious encapsulin and Aquifex aeolicus (AqLS) lumazine synthase protein based on the published crystal structures (www.rcsb.org 2E0Z and 1NQU respectively) were codon optimized for yeast and mammalian expression and synthesized as IDT gene blocks (www.idtdna.com). The 40nm-GEM plasmid for yeast expression was constructed by fusion at the 5’ end of the gene with the yeast INO4 promoter and at the 3’ end (via a Gly-Ser linker) with the T-Sapphire fluorophore (Zapata-Hommer and Griesbeck, 2003) by Gibson assembly into the pRS305 vector (pLH0497: pRS305-PINO4-PfV-GS-Sapphire). The Mammalian expression vector was assembled similarly into the pCDNA3.1 vector (Thermo Fisher) with the CMV2 promoter (pLH611: pCDNA3.1-CMVP2-PfV-GS-Sapphire-GGS). To make a Lentiviral vector (pLH1337: CMV-PfV-Sapphire-IRES-DsRed-WPRE) to express 40nm-GEMs, the PfV-GS-Sapphire sequence was digested from pLH611 and incorporated into a Clontec V4 vector via Gibson assembly. We empirically determined that T-Sapphire was brighter than GFP in the context of GEMs, presumably because the long Stokes-shift of this fluorophore avoids some of the autoquenching that may occur on the crowded surface of these particles. However, this crowded environment also appears to affect the photochemistry of T-Sapphire such that fluorophore excitation is efficient at 488 nm; thus, for imaging purposes, we used settings optimized for GFP (see Imaging below). The 20nm-GEM for yeast expression was assembled by fusion at the 5’ with the yeast HIS3 promoter and at the 3’ (via a Gly-Ser linker) with the T-Sapphire fluorophore by Gibson assembly into the pRS306 vector (pLH1144:pRS306-PHIS3-AqLumSynth-Sapphire). μNS-GFP (PHIS3-GFP-μNS-URA3) fusion was constructed by Gibson assembly of the published N-terminal GFP fusion to the C-terminal fragment of μNS (residues 471–721) (Broering et al., 2005) together with the yeast HIS3 promoter into the pRS306 vector (pLH1125: pRS306-PHIS3-GFP-muNS). The SUMO10-SIM6 yeast reporter(pLH1388:pAV106-pTDH3-mCherry-10xSumo-6xSIM) plasmid was generated by chemical synthesis of mCherry fused to a linked SUMO10SIM6 sequence that was based on the human sequence and then codon optimized for yeast. The mammalian SUMO10-SIM6 was graciously gifted from the lab of Mike Rosen. All yeast plasmids were integrated into the host genome.
Yeast transformation
Yeast strains were created by transforming with a LiAc based approach according to standard methods. BY4741 deletion mutants were obtained from the Yeast Deletion Collection. pLH0497:pRS305-LEU2-PINO4-PfV-GS-Sapphire or pRS306-URA3-PHIS3-PfV-GS-Sapphire was transformed into the collection to allow for screening of mutants or into BY4741 and W303 strains for the rest of the experiments. The cdc28-as1 strain was taken from (Bishop et al., 2000). A list of yeast strains constructed is provided in the STAR Key Resources Table.
Key Resources Table
| REAGENT or RESOURCE | SOURCE | IDENTIFIER |
|---|---|---|
| Antibodies | ||
| Hamartin/TSC1 (D43E2) Rabbit mAb | Cell Signaling Technology | Cat#6935 |
| Bacterial and Virus Strains | ||
| E.coli XL-1 Blue | Agilent | Cat# 200249 |
| Rosetta (DE3) Competent Cells - Novagen | Millipore Sigma | Cat# 70954-3 |
| Chemicals, Peptides, and Recombinant Proteins | ||
| Rapamycin | Tocris Bioscience | Cat# 1292 |
| Cycloheximide | Sigma | Cat# C104450 |
| BMH21 | Sellekchem | Cat# S7718 |
| CX-5461 | Sellekchem | Cat# S2684 |
| SMER 28 | Tocris Bioscience | Cat# 4297 |
| Wortmannin | Cell Signaling Technology | Cat# 9951 |
| TSC1 - SiRNA | Thermo Fisher | Cat# 16708 |
| TSC2 - SiRNA | Thermo Fisher | Ca# 4392420 |
| Trysin Protease | Sigma-Aldrich | Cat# T8658 |
| PURExpress Solution A (-spermidine) and factor mix (10 reaction kit) | NEB | Code# E3313Z |
| Jasplakinolide | Cayman Chemical | CAS# 102396-24-7 |
| Y-27632 2HCL | Selleckchem | Cat# S1049 |
| Latrunculin B | Tocris | Cat# 3974 |
| Critical Commercial Assays | ||
| Gibson Assembly Master mix | NEB | Cat# E2611S |
| Q5 DNA Polymerase | NEB | Cat# M0491S |
| Trans-IT transfection reagent | Mirus | Cat# MIR2704 |
| Lipofectamine RNAiMAX | Thermo-Fisher | Cat# 13778030 |
| Ni-NTA Beads | Qiagen | Cat# 30210 |
| PD-10 desalting column | GE | Cat# 17085101 |
| Amicon Ultra-0.5 Centrifugal Filter Unit with Ultracel-3 membrane | Millipore Sigma | Cat# UFC500308 |
| Alexa Fluor 488 Protein Labeling Kit | Thermo Fisher | Cat#A10235 |
| Lipofectamine 2000 transfection reagent | Thermo-Fisher | Cat# 11668027 |
| Deposited Data | ||
| Subtomogram averages | Electron Microscopy Data Bank | EMD-4372, EMD-4373, EMD-4374, EMD-4375 |
| Tomograms from Figure 5 | Electron Microscopy Data Bank | EMD-4376, EMD-4377 |
| Experimental Models: Cell Lines | ||
| HEK293 | ATCC | Cat#CRL-1573 |
| HEK 293 + PfV GEMs (pLH1337 - lentivrius) | Holt Lab | N/A |
| HEK293 + PfV GEMS (pLH 0611 - transient transfection) | Holt Lab | N/A |
| HEK293T | Jef Boeke Lab | N/A |
| Experimental Models: Organisms/Strains | ||
| S.cerevisiae: BY4741 MATa his21 leu20 met150 ura30 | Jef Boeke Lab | BY4741 |
| S.cerevisiae: W303 MATa leu2-3, 112 trip1-1 can1-100 ura3-1 ade2-1 ade2-1 his3-11-,15 | David Morgan Lab | DOM0090 |
| S.cerevisiae: BY4741 + PINO4::PINO4-PFV-GS-Sapphire-Leu2 | Holt Lab | LH 2129 |
| W303 + ura3::PHIS3-AqLumSynth-Sapphire | Holt Lab | LH3503 |
| BY4741 + NDC1/ndc1::NDC1-tdTomato::KanMX, GFA1/gfa1::GFA1-24PP7; PP7-CP-3xYFP::HIS3 | Karsten Weis Lab | LH3461 |
| W303 + cd28Δ::cdc28-as1,pcl1d::HIS3, pcl2d::URA3, leu2::PINO3-PfV-GS-Sapphire-LEU2 | David Morgan Lab | LH3499 |
| W303 + ura3::PHIS3-GFP-muNS-URA3 | Holt Lab | LH3407 |
| BY4741 + sit4Δ::KANMX, PINO4::PINO4-PfV-GS-Sapphire-LEU2 | Holt Lab | LH3210 |
| BY4741 + fpr1Δ::KAN, PINO4::PINO4-PfV-GS-Sapphire-LEU2 | Holt Lab | LH3290 |
| BY4741 + atg1Δ::KANMX, PINO4::PINO4-PfV-GS-Sapphire-LEU2 | Holt Lab | LH3164 |
| BY4741 + atg13Δ::KANMX, PINO4::PINO4-PfV-GS-Sapphire-LEU2 | Holt Lab | LH3165 |
| BY4741 + atg17Δ::KANMX, PINO4::PINO4-PfV-GS-Sapphire-LEU2 | Holt Lab | LH3166 |
| BY4741 + atg18Δ::KANMX, PINO4::PINO4-PfV-GS-Sapphire-LEU2 | Holt Lab | LH3220 |
| BY4741 + snf1Δ::KANMX, PINO4::PINO4-PfV-GS-Sapphire-LEU2 | Holt Lab | LH3209 |
| BY4741 + rim15Δ::KANMX, PINO4::PINO4-PfV-GS-Sapphire-LEU2 | Holt Lab | LH3157 |
| BY4741 + tap42Δ::KANMX, PINO4::PINO4-PfV-GS-Sapphire-LEU2 | Holt Lab | LH3128 |
| BY4741 + tor1Δ::KANMX, PINO4::PINO4-PfV-GS-Sapphire-LEU2 | Holt Lab | LH3095 |
| BY4741 + sch9Δ::KANMX, PINO4::PINO4-PfV-GS-Sapphire-LEU2 | Holt Lab | LH3097 |
| BY4741 + rts1Δ::KANMX, PINO4::PINO4-PfV-GS-Sapphire-LEU2 | Holt Lab | LH3291 |
| BY4741 + spe4Δ::KANMX, PINO4::PINO4-PfV-GS-Sapphire-LEU2 | Holt Lab | LH3296 |
| BY4741 + pep3Δ::KANMX, PINO4::PINO4-PfV-GS-Sapphire-LEU2 | Holt Lab | LH3295 |
| BY4741 + sap155Δ::KANMX, PINO4::PINO4-PfV-GS-Sapphire-LEU2 | Holt Lab | LH3292 |
| BY4741 + crz1Δ::KANMX, PINO4::PINO4-PfV-GS-Sapphire-LEU2 | Holt Lab | LH3289 |
| BY4741 + cnb1Δ::KANMX, PINO4::PINO4-PfV-GS-Sapphire-LEU2 | Holt Lab | LH3288 |
| BY4741 + cna1Δ::KANMX, PINO4::PINO4-PfV-GS-Sapphire-LEU2 | Holt Lab | LH3286 |
| BY4741 + cna2Δ::KANMX, PINO4::PINO4-PfV-GS-Sapphire-LEU2 | Holt Lab | LH3287 |
| BY4741 + gtr1Δ::KANMX, PINO4::PINO4-PfV-GS-Sapphire-LEU2 | Holt Lab | LH3253 |
| BY4741 + gtr2Δ::KANMX, PINO4::PINO4-PfV-GS-Sapphire-LEU2 | Holt Lab | LH3271 |
| BY4741 + rrd1Δ::KANMX, PINO4::PINO4-PfV-GS-Sapphire-LEU2 | Holt Lab | LH3255 |
| BY4741 + rrd2Δ::KAN, PHIS3::PHIS3 -PfV-GS-Sapphire-URA3 | Holt Lab | LH3256 |
| BY4741 + sfp1Δ::KANMX, PHIS3::PHIS3-PfV-GS-Sapphire-URA3 | Holt Lab | LH3460 |
| BY4741 + ypk3Δ::KANMX, PHIS3::PHIS3-PfV-GS-Sapphire-URA3 | Holt Lab | LH3605 |
| BY4741 + yak1Δ::KANMX, PINO4::PHIS3-PfV-GS-Sapphire-URA3 | Holt Lab | LH3446 |
| BY4741 + sln1Δ::KANMX, PHIS3::PHIS3-PfV-GS-Sapphire-URA3 | Holt Lab | LH3609 |
| BY4741 + hog1Δ::KANMX, PINO4::PINO4-PfV-GS-Sapphire-LEU2 | Holt Lab | LH3653 |
| BY4741 + sac1Δ::KANMX, PINO4::PINO4-PfV-GS-Sapphire-LEU2 | Holt Lab | LH3268 |
| BY4741 + pmr1Δ::KANMX, PINO4::PINO4-PfV-GS-Sapphire-LEU2 | Holt Lab | LH3263 |
| BY4741 + arf1Δ::KANMX, PINO4::PINO4-PfV-GS-Sapphire-LEU2 | Holt Lab | LH3305 |
| BY4741 + glc7Δ::KANMX, PINO4::PINO4-PfV-GS-Sapphire-LEU2 | Holt Lab | LH3332 |
| BY4741 + cdc55Δ::KANMX, PINO4::PINO4-PfV-GS-Sapphire-LEU2 | Holt Lab | LH3333 |
| BY4741 + gcn2Δ::KANMX, PINO4::PINO4-PfV-GS-Sapphire-LEU2 | Holt Lab | LH3338 |
| BY4741 + npr1Δ::KANMX, PINO4::PINO4-PfV-GS-Sapphire-LEU2 | Holt Lab | LH3341 |
| BY4741 + ypq1Δ::KANMX, PINO4::PINO4-PfV-GS-Sapphire-LEU2 | Holt Lab | LH3345 |
| BY4741 + gat1Δ::KANMX, PINO4::PINO4-PfV-GS-Sapphire-LEU2 | Holt Lab | LH3339 |
| BY4741 + gat2Δ::KANMX, PINO4::PINO4-PfV-GS-Sapphire-LEU2 | Holt Lab | LH3340 |
| BY4741 + mep1Δ::KANMX, PINO4::PINO4-PfV-GS-Sapphire-LEU2 | Holt Lab | LH3342 |
| BY4741 + mep2Δ::KANMX, PINO4::PINO4-PfV-GS-Sapphire-LEU2 | Holt Lab | LH3343 |
| BY4741 + mep3Δ::KANMX, PINO4::PINO4-PfV-GS-Sapphire-LEU2 | Holt Lab | LH3344 |
| BY4741 + reg1Δ::KANMX, PINO4::PINO4-PfV-GS-Sapphire-LEU2 | Holt Lab | LH3371 |
| BY4741 + gln3Δ::KANMX, PINO4::PINO4-PfV-GS-Sapphire-LEU2 | Holt Lab | LH3412 |
| BY4741 + ssd1Δ::KANMX, PINO4::PINO4-PfV-GS-Sapphire-LEU2 | Holt Lab | LH3334 |
| BY4741 + msn2Δ::KANMX, PINO4::PINO4-PfV-GS-Sapphire-LEU2 | Holt Lab | LH3158 |
| BY4741 + msn4Δ::KANMX, PHIS3::PHIS3-PfV-GS-Sapphire-URA3 | Holt Lab | LH4354 |
| BY4741 + gis1Δ::KANMX, PHIS3::PHIS3-PfV-GS-Sapphire-URA3 | Holt Lab | LH3455 |
| W303 + ura3::PTDH3-mCherry-Sumo10-Sim6-URA3 | Holt Lab | LH3922 |
| BY4741 + PTDH3::PTDH3-mCherry-Sum10Sim6-URA3 | Holt Lab | LH3914 |
| BY4741 + sfp1Δ::KANMX, PTDH3::PTDH3-mCherry-Sum10Sim6-URA3 | Holt Lab | LH3915 |
| BY4741 + atg13Δ::KANMX, PTDH3::PTDH3-mCherry-Sum10Sim6-URA3 | Holt Lab | LH3916 |
| BY4741 + atg17Δ::KANMX, PTDH3::PTDH3-mCherry-Sum10Sim6-URA3 | Holt Lab | LH3917 |
| BY4741 + rim15Δ::KANMX, PTDH3::PTDH3-mCherry-Sum10Sim6-URA3 | Holt Lab | LH3918 |
| BY4741 + atg1Δ::KANMX, PTDH3::PTDH3-mCherry-Sum10Sim6-URA3 | Holt Lab | LH3919 |
| BY4741 + sit4Δ::KANMX, PTDH3::PTDH3-mCherry-Sum10Sim6-URA3 | Holt Lab | LH3920 |
| BY4741 + fpr1Δ::KANMX, PTDH3::PTDH3-mCherry-Sum10Sim6-URA3 | Holt Lab | LH3921 |
| W303 + GFA1/gfa1::GFA1-24PP7; PP7-CP-3xYFP::HIS3 | Karsten Weis Lab | LH3461 |
| W303 + ura3::pRS306-pHIS3-2xGFP | Holt Lab | LH3349 |
| Oligonucleotides | ||
| TSC1 siRNA | Thermo Fisher | AM16708 |
| Recombinant DNA | ||
| Yeast plasmid: pAV106-pTDH3-mCherry-10xSumo-6xSIM | Holt Lab | pLH1392 |
| Mammalian plasmid: pCDNA3.1-CMV-Sumo10Sim6 | Holt Lab | pLH1393 |
| pRS305-Leu2-PINO4-PfV-GS-Sapphire | Holt Lab | pLH0497 |
| pRS306-URA3-PHIS3-AqLumSynth -Sapphire | Holt Lab | pLH1144 |
| pRS306-URA3-PHIS3-PfV-GS-Sapphire | Holt Lab | pLH1123 |
| Mammalian: pCDNA3.1-CMVP2-PfV-GS-Sapphire-GGS | Holt Lab | pLH0611 |
| Mammalian: CMB-PfV-Sapphire-IRES-DSRed-WPRE | Holt Lab | pLH1337 |
| pRS306-PHIS3-GFP-muNS | Holt Lab | pLH1125 |
| pRS306-pHIS3-2xGFP-tURA3 | Holt Lab | pLH1115 |
| Software and Algorithms | ||
| FIJI (FIJI is just ImageJ) | Schindelin et al., 2012 | https://idp.nature.com/authorize?response_type=cookie&client_id=grover&redirect_uri=http%3A%2F%2Fwww.nature.com%2Fnmeth%2Fjournal%2Fv9%2Fn7%2Ffull%2Fnmeth.2019.html. |
| Image J2 | Schindelin et al., 2015 | https://onlinelibrary.wiley.com/doi/10.1002/mrd.22489/full |
| MOSAIC for ImageJ | Shivanandan et al., 2013 | https://bmcbioinformatics.biomedcentral.com/articles/10.1186/1471-2105-14-349 |
| Matlab2016b | Mathworks (2016). | https://www.mathworks.com/products/matlab.html |
| Nikon Elements | Nikon Instruments (2017) | https://www.nikoninstruments.com/Products/Software |
Virus production and cell transduction
In order to create lentivirus, 800,000 HEK293T cells were plated in 10 mL media in 15 cm dishes. The next day, each well was transfected with 24 μg vector, 1.2 μg tat, 1.2 μg rev, 1.2 μg gag/pol, and 2.4 μg of vsv-g DNA with 90μL trans-IT in 2 mL DMEM. Supernatants were collected at 24, 48, and 72 h after transfection and stored at 4 °C until they were spun at 20,000 rpm (52,931 rcf) for 90 minutes on a Beckman L-80 Ultracentrifuge. Viral pellets were resuspended in 1/50th of their original volume in DMEM (with 10 % FBS) and stored at −80 °C until their use. Stable HEK293 cell lines were created by transfection with (pLH611: pCDNA3.1-CMVP2-PfV-GS-Sapphire-GGS) followed by neomycin selection. Additional HEK293 cell lines were created by lentiviral transduction with pLH1337-CMV-PfV-Sapphire-IRES-DsRed-WPRE. No differences in terms of cellular rheology were seen between these different methods. In order to transduce these cell lines, 50,000 cells were plated in 2 mL of media in 6 well plates. The next day, media was removed and replaced with media containing 8 μg/mL polybrene. Between 1–20 μL of concentrated virus was added to the well and then the media was replaced after 24 hours.
Drug treatments
In order to inhibit mTORC1 signaling, we treated yeast or mammalian cells with rapamycin (Tocris Bioscience, Avonmouth, Bristol, UK) at 1 μM for 2 h in yeast and 3 h in mammalian cells. To block translation we added cycloheximide to final conecentartion of 1 μM (Sigma-Aldrich, Allentown PA). In order to block ribosome production in HEK293 cells, we treated cells with PolI inhibitors BMH21 and CX5461 (Selleckchem, Houston, Texas, USA) at concentrations of 10 μM and 500 nM, respectively for 3 h. In order to increase autophagy in HEK293 cells, we treated cells with SMER28 (Tocris Bioscience, Avonmouth, Bristol, UK) at a concentration of 5 μM for 3 h. In order to decrease autophagy in HEK293 cells, we treated with 800nM Wortmannin (Cell Signaling Technology, Danvers, MA, USA) for 2 h. In order to de-polymerize actin and microtubules in yeast we incubated the cells with 200 μM latrunculinA and 50 μM nocodazole (Tocris) for 30 min. In order to depolymerize actin in HEK293 cells, we treated with 10 μM latrunculin A (tocris) for 20 min. In order to freeze the actin cytoskeleton, we treated with 10 μM y27632 (selleckchem) for 10 min then added jasplakinolide (Cayman) and latrunculinB (Tocris) to final concentrations of 8 μM jasplakinolide and 5 μM latrunculinB and imaged immediately after. This treatment is called the JLY cocktail (Peng et al., 2011). All stocks were prepared in DMSO and stored at −20 °C until needed. DMSO was used as a vehicle control in all experiments.
Imaging and direct particle tracking
Single particle tracking in Saccharomyces cerevisiae was performed for the 20nm-GEMs, 40nm-GEMs, AqLS particles, GFA1 mRNA particles, and μNS. The particles were imaged using TIRF Nikon TI Eclipse microscope in partial TIRF mode at 488 nm excitation, and fluorescence was recorded with a scMOS camera (Zyla, Andor) with a 100x objective (pixel size: 0.093 μm), with a time step that depended on the particles. The GEMs were imaged at a rate of one image every 10 ms, whereas both the RNA particles and the μNS were imaged with a 100 ms time step.
Single particle tracking in HEK293 cells was performed for 40nm-GEMs using an Andor Yokogawa CSU-X confocal spinning disc on a Nikon TI Eclipse microscope and fluorescence was recorded with a sCMOS Prime95B camera (Photometrics) with a 100x objective (pixel size: 0.11μm), at a 10 ms image capture rate.
The tracking of particles was performed with the Mosaic suite of FIJI, using the following typical parameters: radius =3, cutoff = 0, 10 % of fluorescence intensity, a link range of 1, and a maximum displacement of 8 px, assuming Brownian dynamics.
Extraction of the rheological parameters
Various parameters were extracted from the particle trajectories. For every trajectory, we calculated the time-averaged mean-square displacement (MSD), as defined in (Munder et al., 2016a) as well as the ensemble-average of the time-averaged MSD. As measured in the insets of figure 2D and 2E, where the ensemble-averaged MSD is plotted as a function of time in a log-log plot, the diffusion of the tracer particle is subdiffusive, and generally obeys the following law:
| (1) |
where α is the power exponent of the anomalous diffusion, and α < 1 in the case of a subdiffusive behavior. In this case, the apparent diffusion coefficient, K, is not in units of μm 2/s, but rather in units of μm 2/sα.
To characterize individual particle trajectories, we calculated apparent diffusion coefficients by fitting MSD with a linear (diffusive) time dependence at short time scales (less than 100 ms for GEMs, 1 s for mRNP and μNS particles). To do this, we calculated the MSD and truncated it to the first 10 points, and fit` it with the following linear relationship:
| (2) |
where is the effective coefficient of diffusion of the tracer particle, and plotted the distribution of this effective diffusion coefficient. We used the Kolmogorov-Smirnov statistical test to assess the statistical difference between distributions (kstest2 function in MATLAB).
Culture saturation and nutrient depletion experiments
Culture O.D. was measured from 0.2 to 5.2 on a Thermo Scientific Nano-Drop One spectrophotometer followed by GEM tracking as previously described. To measure the effects of depletion of amino acids, carbon, and nitrogen, synthetic complete media was prepared without 20 g/L dextrose (carbon starvation), without Drop-put mix complete w/o Yeast Nitrogen Base (US Biological), or without Yeast Nitrogen Base w/o amino acids (Difco). Since dextrose is the major source of osmolytes in SCD media, 18 g/L of sorbitol was added to restore regular osmolarity in the carbon starvation condition. In order to ensure that all dextrose-containing media was removed, cells were spun down once at 3000 RPM then resuspended in starvation media. After plating on ConcanavalinA-treated imaging dishes, the cells were then washed 4 times in fresh starvation media.
mTORC1 overexpression - TSC1 siRNA experiments
TSC1 (s14433 or s14434) was targeted by Silencer Select siRNAs from Thermo Fisher Scientific. 75 pmoles of siRNA were transfected using Lipofectamine RNAiMAX transfection reagent from Thermo Fisher Scientific as per manufacturer’s instructions. Cells containing GEMs were assayed for diffusion at 72 h post transfection. Knockdown was validated by Western blot using Hamartin (TSC1) (D43E2) Rabbit mAb #6935 from Cell Signaling Technologies using standard techniques.
40nm- and 20nm-GEM purifcation for negative stain EM
Purification was performed at 4°C, unless otherwise noted. Two liters of yeast cells were grown overnight then lysed by cryogenic lysis in buffer B1 (20 mM Tris–HCl (pH 7.5), 10 mM MgCl2, 50 mM NH4Cl, 10 mM 2-mercapthoethanol, 10% glycerol (v/v), 1 mM PMSF, 2 mM spermidine). Cell debris removed by centrifugation at 9200 g for 25 min. Next, the lysate was warmed to 55°C for 30 min. The supernatant was further clarified by centrifugation at 38,900g for 1 h. The partially purified 40nm-GEM or 20nm-GEM particles were pelleted by ultracentrifugation at 185,000g for 3 h and then the particles were resuspended in buffer B1 (20 mM Tris–HCl (pH 7.5), 10 mM MgCl2, 50 mM NH4Cl, 10 mM 2-mercapthoethanol, 10% glycerol (v/v), 1 mM PMSF, 2 mM spermidine). This suspension was gently mixed with 20% Triton X-100 in KCl buffer (20 mM Tris–HCl (pH 7.5), 10 mM MgCl2, 50 mM NH4Cl, 10 mM 2-mercapthoethanol, 10% glycerol (v/v), 1 mM PMSF, 2 mM spermidine, 2.5 M KCl) at 30°C. Then the suspension of 40nm-GEM or 20nm-GEM particles was carefully overlaid on a cushion of 20% sucrose in buffer B1 and pelleted by ultracentrifugation at 185,000g for 20 h. Next, the particles were resuspended in buffer B2 (20 mM Tris–HCl (pH 7.5), 5 mM MgCl2, 50 mM NH4Cl, 10 mM 2-mercapthoethanol, 10% glycerol (v/v), 1 mM PMSF, 2 mM spermidine) and then gently mixed with buffer C (20 mM Tris–HCl (pH 7.5), 5 mM MgCl2, 50 mM NH4Cl, 10 mM 2-mercapthoethanol, 10% glycerol (v/v), 1 mM PMSF, 1.5 M KCl, 2 mM puromycin, 2 mM guanosine triphosphate) at 30°C. Finally, the particles were overlaid carefully on a cushion of 25% glycerol in buffer B2 and pelleted by ultracentrifugation at 185,000g for 15 h.
Negative stain transmission electron microscopy
Purified particles were deposited on carbon-coated 400 mesh copper/rhodium grids (Ted Pella Inc., Redding, CA), stained with 1% aqueous uranyl acetate, examined in a Philips CM-12 electron microscope and photographed with a Gatan (4k x2.7k) digital camera.
Cryo-EM grid preparation and data acquisition
W303 S. cerevisiae were grown on YPD plates for two days, then suspended in SCD media at low cell concentration by serial dilution and grown overnight at 30 ° C on a roller drum to an OD of 0.25. Cells were then incubated with 1μM rapamycin in DMSO or only DMSO (control) for 2 h until an OD of 0.55. Cells were frozen onto EM grids between 2 and 2.5 h after addition of the drug. 4 μL of culture was applied to R2/1 holey carbon copper EM grids (Quantifoil) and immediately vitrified by plunge-freezing into a liquid ethane/propane mixture with a Vitrobot Mark IV (FEI, The Netherlands) using a blot time of 10 s, a blot force of 10, and a chamber conditioned to 25 °C and 90% humidity. EM grids with vitrified yeast cells were transferred either to a Quanta or Scios dual-beam microscope (both FEI, The Netherlands) for focused ion beam micromachining. The vitrified cells were platinum coated with organometallic platinum and subsequently thinned by scanning gallium ions in a stepwise fashion from both sides. This yielded vitrified cellular sections of 100–200 nm thickness that were suitable for cryo-electron tomography (Schaffer et al., 2017). EM grids with milled samples were transferred to a Titan Krios TEM (FEI, The Netherlands) operated at an acceleration voltage of 300 kV, an object pixel size of 3.42 Å and a nominal defocus of −6 μm. The TEM was equipped with a Quantum energy filter (Gatan) and a K2 summit direct electron detector (Gatan) operated in movie mode (12 frames per second). Single-axis tilt series were acquired in SerialEM (Mastronarde, 2005) using a bi-directional tilt scheme covering a tilting range of approximately −60 ° to 60 ° with a 2 ° angular increment. Depending on the pre-tilt of cellular sections in the TEM, the two tomogram halves were connected at either +20 ° or −20 ° tilt. The cumulative electron dose for a tilt series was 70–120 electrons per Å2, depending on the sample thickness.
Tomogram reconstruction
Frames from the K2 direct detector were aligned with MotionCor2 (Zheng et al., 2017) using 3×3 patches for local alignment. For each tilt series, the resulting frame-aligned projections were sorted according to their tilt angles and compiled into an image stack that was loaded into IMOD for tilt series alignment via patch tracking. Projection-wise translations and rotations determined during patch tracking were extracted from IMOD ‘s output files and used for tilt series alignment in TOM/AV3 (Förster and Hegerl, 2007; Nickell et al., 2005). Phase reversals introduced by the contrast transfer function (CTF) were determined on each individual projection using strip-based periodogram averaging (Eibauer et al., 2012) in TOM/AV3 and corrected in PyTom (Hrabe et al., 2012). Finally, the aligned CTF-corrected tilt series was weighted for subsequent reconstruction of tomographic volumes via weighted back projection (AV3/TOM). For reconstruction of binned tomograms, the tilt series was scaled to 2.1 nm in Fourier space (AV3/TOM).
Determination of the cytosolic volume in tomograms
Binary masks encompassing exclusively the cytosolic volume were generated by manual segmentation of tomograms in Amira (FEI, The Netherlands). As each voxel corresponds to a volume of (2.1 nm) 3 = 9.26 nm 3, the exact cytosolic volume included within the tomogram could be obtained by counting the voxels encompassed by the mask.
Subtomogram analysis
Ribosomes:
To generate a data-driven de novo template for correlation-based ribosome localization, 500 ribosomes were manually selected from one of the tomograms and reconstructed as described below. The subtomograms were iteratively aligned using fast rotational matching (FRM) (Chen et al., 2013) implemented in PyTom with a featureless sphere as a starting reference (Figure S4A). The average converged into a ribosome within 12 iterations and was subsequently used as a template for correlation based localization of ribosomes (Frangakis et al., 2002) in all tomograms. For each tomogram, the cross-correlation function resulting from template matching was masked to include only the cytosolic volume of the cell (Figure S4B) and the 5000 highest-scoring peaks were extracted. To avoid multiple detection events for the same ribosome, a minimal Euclidean distance of 18.9 nm (9 voxels) between peaks was imposed. The distribution of correlation coefficients for the extracted peaks showed clear separation of coefficients corresponding to true and false positives (Figure S4C). This allowed fitting of a Gaussian function to the distribution of coefficients corresponding to true positives and thus quantification of ribosome abundance within the cytosolic volume.
For detailed analysis of ribosome structures, all ribosomal particles with correlation coefficients better than one standard deviation below the mean of the Gaussian fit were retained and reconstructed at full spatial resolution in PyTom from the CTF-corrected, weighted and aligned projections covering approximately the first half of the tilt series. Projections corresponding to the second half of the tilt series were excluded at this step due to excessive beam damage that dampens high-resolution signal. The reconstructed subtomograms were aligned until convergence with Relion’s gold standard “3D auto-refine” functionality, which is now available for subtomograms (Bharat et al., 2015). During subtomogram averaging, Relion’s 3D CTF model was used to compensate for beam damage with the recommended B-factor of −4 per electron per Å 2. Resolution of the resulting averages was estimated based on Fourier shell cross-correlation (FSC) of two completely independent halves of the data using FSC = 0.143 as the cutoff criterion. For computation of the difference density between ribosome structures from control and rapamycin-treated cells, the averages were filtered to 15 Å resolution, normalized according to density mean and density standard deviation, and subtracted from each other. The UCSF Chimera software package (Goddard et al., 2007) was used for visualization of EM densities.
GEMs:
GEMs are readily visible in tomograms as high-contrast sphere-like particles (Figure S3D). Consequently, template matching against a hollow sphere of appropriate size in combination with visual inspection of the 50 highest scoring cross-correlation peaks in the cytosolic volume allowed highly specific localization of GEMs in the tomograms. Subtomogram reconstruction, alignment and resolution estimation were performed as described for the ribosome, with the only exception that icosahedral symmetry was applied during subtomogram alignment.
FCS and coefficient of diffusion of 2xGFP
A custom-modified inverted microscope (Nikon Eclipse Ti; Nikon Instruments) was used for fluorescence correlation spectroscopy (FCS) measurements. Prior to each measurement, a focal volume within a cell was located by eGFP epifluorescence. A 100-ps pulsed 482 nm diode laser (PicoQuant) was coupled to a single-mode fiber and collimated to a 4-mm diameter, then focused on the sample through a 100× objective (CFI Apo 100× Oil immersion TIRF NA 1.49; Nikon Instruments), with the laser power of 0.2 μW before the objective. The focal volume was calibrated with a fluorescent dye with a known diffusion coefficient (Alexa 488, D = 435 μm 2/s (Petrášek and Schwille, 2008). Each FCS measurement was the average of 10–20 cells. Fluorescence emitted from the sample was passed through a 50-μm pinhole (Thorlabs), and focused to a bandpass-filtered single-photon avalanche diode with a 150 × 150 μm element (PDM module; Optoelectronic Components). The resulting fluorescence fluctuation was processed by a hardware correlator (Correlator.com), which generated the autocorrelation function. See table S1 for results and more details on the fitting procedure of the autocorrelation function.
FCS calculations
FCS data were fit using a “blinking and anomalous diffusion” model, that has the following form (Brazda et al., 2011):
| (4) |
The term on the left before the is the blinking term corresponding to the properties of GFP. In this term, was measured independently from whole cell lysate,. The term on the right corresponds to the anomalous 3D diffusion of GFP, where is the particle residence time in the focus volume,. and s/w are the radial and axial dimensions of the 3D Gaussian laser focus, respectively, and they were measured using a dye with a known diffusion coefficient (Alexa Fluor 488). In practical terms, s does not affect the fit, and was fixed to be s=10. The result of the fit is summarized in table 1, and yields and, which are not significantly different (3 biological replicates, n ≥ 10 cells per condition) (Table S1). Note that the anomalous diffusion exponent a is 0.8 in both cases, close to the measured anomalous parameter measured for GEMs. We chose an anomalous model, as commonly used in the literature to describe motion of GFP in a cell (Slaughter et al., 2007), and as it yielded a better fit than the normal diffusion model.
Osmotic perturbation experiments and cell volume measurement
In order to calculate the dependence of GEM diffusion on the volume fraction of crowding agent, we performed hyper- and hypo-osmotic stresses (see model below). LH2129 (BY4741 + PINO4::PINO4-PfV-GS-Sapphire-LEU2) cells were grown in log phase to an O.D. of 0.3, then spun down for 1 min at 10000 rpm. Cells were washed with fresh medium, and placed in synthetic complete with dextrose medium (CSM) complemented with 0 M, 0.5 M, 1 M, 1.5 M or 2 M of sorbitol. A subset of cells were directly (within 15 min) imaged for diffusion, and phase contrast images were acquired to assess cell area as a proxy for cell volume. The rest of the cells were left at various O.D.s in a shaker at 30 °C to adapt to the osmotic stress and grow overnight. The next day, cells were imaged for diffusion and cell volume (figure S7A), to check that cell volume and the diffusion of particles had recovered to their nominal values. These pre-adapted cells (which had built up a high concentration of internal osmolyte) were then spun down and placed in regular CSM, creating a hypo-osmotic stress of −0.5 M, −1 M, 1.5 M and −2 M, and immediately imaged for diffusion and cell volume. The same process was used for HEK293 cells (figure S7B), with osmotic stress of 0.25 M and 0.5 M sorbitol. In this case, cells were trypsinized and their volume measured from their area when the cells were spherical.
SUMO-SIM protein purification
Tandem repeats of Small Ubiquitin-like Modifier (SUMO10) and SUMO Interaction Motif (SIM6) proteins were expressed in Rosetta2 DE3 competent cells by induction with 100 μM IPTG for 18 hr at 16°C. 4 L of bacterial culture were collected and centrifuged at 4000 rpm for 20 min at 4°C. The cell pellet was resuspended in 100 mL cold lysis buffer (50 mM NaH2PO4, 300 mM NaCl, 10 mM imidazole pH 7.6) containing 1 mM PMSF. After sonication, the lysate was centrifuged at 12000 rpm for 30 min at 4°C. The supernatant was mixed with 8 mL of 50% slurry of Ni-NTA beads (Qiagen), and incubated at 4°C for 2 h. The bound beads were collected by centrifugation at 500g for 1 min and rinsed 3 × with 30 mL bacterial wash buffer containing (50mM NaH2PO4, 300mM NaCl, 20 mM imidazole pH7.6). Proteins were then eluted with 8 mL elution buffer (50mM NaH2PO4, 300mM NaCl, 500 mM imidazole pH7.6) and exchanged into 2 mL of SUMO-SIM protein buffer (150 mM KCl, 20 mM HEPES pH 7, 1 mM MgCl2, 1 mM EGTA, 1 mM DTT) using a PD10 column (GE Healthcare), followed by further concentrating to 300–600 μM with Amicon Ultra 30K device (Millipore) at 4°C.
SIM6 was labelled with Alexa Fluor® 488. The protein was conjugated with Alexa Fluor® 488 using a large scale protein labeling kits (A10235, Thermo Scientific).
In vitro phase separation experiment
In order to determine if crowding by ribosomes affects SUMO/SIM phase separation in vitro, we added purified ribosomes from an in vitro translation kit (IVT) (NEB, Ipswich, MA) to a mix of 6 μM SUMO10 and 10 μM SIM-Alexa Fluor 488 such that the concentrations of each individual SUMO domain and SIM motif were 60 μM. Ribosomes were added at the same concentrations measured in vivo by cryo-ET as well as at an intermediate concentration. Ribosomes, SUMO, and SIM were mixed in a well of a 384 well imaging plate, the top was covered with clear tape and then the plate was allowed to sit overnight in order to reach a steady-state before imaging. The plate was imaged on an Andor Yokogawa CSU-X confocal spinning disc on a Nikon TI Eclipse microscope and GFP fluorescence was recorded with an scMOS (Zyla, Andor) camera with a 100x objective (pixel size: 0.1μm). Images were loaded into FIJI and the partition coefficient (amount of protein that has condensed into liquid droplets versus protein dissolved in the bulk aqueous phase) was calculated by segmenting the image into two regions: bright condensed droplets and background. The total fluorescence intensity was measured in each region using the raw integrated density value, and the partition coefficient was calculated as the ratio of intensities in the condensed phase versus the bulk phase, then plotted in MATLAB.
In vivo phase separation experiments
In order to determine the effects of changes in ribosome concentration via mTORC1 signaling on phase separation, we expressed a mCherry-SUMO10-SIM6 fusion protein in yeast (pLH1392) and mammalian cells (pLH 1393). Wild-type and mutant yeast cells were grown from dilutions of single colonies overnight to log phase and then treated with rapamycin for 2 h. Sorbitol was added in the last ten min for the indicated conditions. Mammalian cells were treated for 3 h with rapamycin with sorbitol added in the final 30 min where indicated. TIRF microscopy on a Nikon-TI microscope was performed using a 561 nm laser sample through a 100x objective (CFI Apo 100x Oil immersion TIRF NA 1.49; Nikon Instruments). Images were segmented in FIJI to determine the 1) average size of droplets, 2) number of droplets and 3) number of cells. In the actute rapamycin / sobitol treatment conditions, we then used these data to define the total phase separated area as:
| (3) |
Next, we expressed the mCherry-SUMO10-SIM6 fusion protein in the ribosome biogenesis / autophagy mutants that we found to have an effect on crowding. We reasoned that these mutants would be a better test of our hypothesis, as they do not suffer the acute effects of rapamycin but rather sit at steady state. In these mutants, we measured the likelihood of having a droplet of any size and related this probability to the effects of crowding and protein concentration by flow.
SUMO-SIM protein concentration and yeast cell size
Cells were grown to log phase between O.D. 0.1 and 0.4 and then analyzed on a SONY SH800 Cell Sorter. Fluorescence was recorded for the mCherry-tagged SUMO10-SIM6 fusion protein for every cell and then the average fluorescence intensity was extracted using Flow-Jo. These values were normalized to wild-type and then averaged across replicates.
Quantification and Statistical Analysis
Distributions of effective diffusion coefficients were compared using the Kolmogorov-Smirnov test in MATLAB using the kstest2 function. Comparison of anomalous exponenents between and within yeast and mammalian treatments was conducted using a student’s t-test.
Crowding regulation through control of ribosome concentration Model Basis
In the following, we derive a model to describe the relationship between cellular crowding and the effectuve diffusion of a mesoscale tracer particle, like our 40nm-GEMs. We assume that there is a major source of crowding within the cell that impacts the mesoscale viscosity. We express the diffusion of the tracer particle as a function of volume fraction of the major crowder source, ϕ, using the phenomenological Doolittle equation (Doolittle, 1952):
| (5) |
where is the coefficient of diffusion in an infinitely diluted solution, is the maximum fraction of the crowder, and is a constant. We write the volume fraction for the major source of crowder as:
| (6) |
where is the volume occupied by the major source of crowding, the volume occupied by other macromolecules, and is the volume occupied by water in the cell. v is the volume of the cell. The maximum fraction of crowder in the cell is reached when the volume of water is close to 0, such that.
Validation of Doolittle equation and determination of parameters using instantaneous volume change through osmotic stress
During an instantaneous volume change as a result of an osmotic stress, the total number of macromolecules remains, to a first approximation, constant. The cell volume changes because of a passive outflow (hyper-osmotic stress) or inflow (hypo-osmotic stress) of water. We denote the volume fraction of macromolecules before the osmotic shock, when the cell volume is:
| (7) |
Denoting the normalized cell volume, one can express:
| (8) |
Note that the diffusion coefficient in equation 5 does not correspond to the coefficient of diffusion under normal conditions, but corresponds to the coefficient of diffusion for an infinitely diluted solution of macromolecules. Rather, the coefficient of diffusion under normal conditions, which we denote, is defined when
| (9) |
This leads to the formula that describes the instantaneous change of the coefficient of diffusion upon a given volume change:
| (10) |
We used equation 10 to fit the coefficient of diffusion for 40nm-GEMs under hypo- and hyper-osmotic stresses (see figure 7B–C). The model is in good agreement with our data (), and gives parameters for S. cerevisiae,.
This number means that, under normal conditions, the fraction of crowder inside the cell is about 50% the maximum crowding.
We performed the same osmotic stress experiment on HEK293 cells, and initially measured different parameters. Osmotic stress is known to strongly affect the actin cytoskeleton in mammalian cells, which could affect the interaction parameter, , which was confirmed when we treated the cells with LatrunculinA at the same time we did the osmotic stress: the interaction parameter of the GEMs with the environment increased. When the actin cytoskeleton was stabilized with the JLY cocktail (Peng et al., 2011), we found that the two parameters of the model were closer to the yeast values: is very similar to yeast, suggesting that the interactions of the GEMs with the microenvironment is the same, and is lower, suggesting that mammalian cells are less crowded.
This result indicates that 40nm-GEMs seem may interact with the same species inside both S. cerevisiae and HEK293 cells in a diffusion-dependent manner.
Homeostatic crowding, and homeostasis breaking under a rapamycin treatment
What is the major source of crowding inside the cell? Our genetic perturbations suggesti that ribosomes play a crucial role in crowding regulation. Therefore, we can rewrite the volume fraction of crowder, considering ribosomes as the major crowder:
| (11) |
with being the typical volume of a single ribosome.
This leads to the following equation:
| (12) |
We used this equation with the parameters measured by osmotic stress to predict how particular mutations or chemical treatment should affect crowding, measured through the coefficient of diffusion, as a function of ribosome concentration. The ribosome concentration is determined by its number in the cells, , and the volume of the cell,. We measured the number of ribosomes either by direct counting with in situ cryo-ET, or by measuring their relative amount compared to wild-type or normal conditions by quantification of a total extracted nucleic acid on an agarose gel (see figure S7D–F). The cell volume was determined through brightfield measurements.
Figure 6 displays the model prediction for both S. cerevisiae and HEK293 cells, which is in very good agreement with the measured data. This suggests that:
Ribosomes are indeed the main determinant of cytosolic crowding inside the cell and can be considered as hard spheres.
The cytoplasm of mammalian cells and yeasts behave similarly in terms of crowding.
Data and software availability
All subtomogram averages presented in this study have been deposited in the Electron Microscopy Data Bank (EMD-4372, EMD-4373, EMD-4374, EMD-4375), along with the tomograms from figure 5 (EMD-4376, EMD-4377).
Supplementary Material
Results of fitting the blinking anomalous diffusion model to FCS data.
Mutants in the yeast BY4741 background expressing pLH0497. Basal change in diffusion coefficient, and change in the magnitude of the rapamycin effect were measured. Genes deletions that result in a change in basal or greater than 0.5 are highlighted in orange.
The two parameters presented are the change in basal gene diffusion, measured as the ratio of 40nm-GEM diffusion in the mutant as compared to the wild type:
and the magnitude of the rapamycin effect (ε ), measured as the ratio of change in after rapamycin treatment for the mutant vs the wild type change (equation formulated such that ε = 0 indicates no change and ε = 1 indicates that the rapamycin effect is completely lost):
(A) 20nm-GEMs are observed to be 15.39 +/− 0.84 nm by negative stain EM. (B) 40nm-GEMs, which are seen to be 41 nm in high-accuracy in situ cryo-ET, appear to be 37.23 +/− 3.69nm by negative stain EM. (C) The median track length for 40nm-GEMs in DMSO and rapamycin treatment is similar at 35.2 +/− 2.1 and 34.8 +/− 2.2 frames, respectively. Track lengths < 10 displacements were excluded from all analyses (grey shaded area).
(A) The anomalous exponent, a measure of subdiffusive motion, is similar for rapamycin and DMSO treatment in both yeast and HEK293 cells (according a Student’s T-test) but is higher in HEK293 compared to yeast, indicating that mammalian cells are less subdiffusive (p=0.03). (B-I) Cell volume increase, translation, and cytoskeletal perturbations do not explain rapamycin-dependent effects on GEM behavior. (B) Effect of culture saturation on the diffusion coefficent of 40nm-GEMs in BY4741 yeast cells (Normalized Units (N.U.)) (C) Effects of 2 hours of amino acid depletion, 30 minutes of carbon starvation and 30 minutes of nitrogen starvation on the diffusion coefficeint of 40nm-GEMs in BY4741 cells. (D) Effect of rapamycin treatment on the diffusion coefficent of 40nm-GEMs in BY4741 cells over 4 hours. (E) Combined effects of starvation and rapamcyin treatment on the diffusion coefficient of the MS2-tagged GFA1 mRNA. (F and G) Change in coefficient of diffusion (F) and normalized volume (G) over time for rapamycin treatment (orange), cyclohexamide treatment (green), and cell cycle inhibition of the conditional mutant cdc28-as with NMPP1 (blue). (H and I) Actin and microtubule perturbations alter the diffusion of 40nm-GEMs in yeast and mammalian cells but do not abolish the effect of rapamycin. (J) TSC1 was targeted using Silencer Select siRNA (Thermo Fisher). Knockdown was validated by Western blot for Hamartin/TSC1 with a tubulin control using standard techniques (see methods).”
(A) GEM subtomogram averages obtained for DMSO-treated control (left panels) and rapamycin treated (right panels) cells filtered to 26.3 Å resolution. In the central two panels, averages have been sliced open to show the interiors. (B) Fourier shell correlation (FSC) between subtomogram averages derived from two independent halves of the data (gold standard) for control (blue) and rapamycin-treated (orange) cells. Resolution was determined to 26.3 Å in both cases using the FSC = 0.143 resolution criterion. (C) FSC between the two resolution-limited subtomogram averages obtained for control and rapamycin-treated cells. High correlation (FSC > 0.5) within the trustworthy resolution range suggests that GEM structures under both conditions are identical. (D) Gallery of individual GEM particles from control (lower row) and rapamycin-treated (upper row) cells. Each image corresponds to a central tomogram slice through the GEM particle. The amount of cargo within the GEM lumen varies.
(A) 500 manually selected ribosome-containing subtomograms were iteratively aligned with a sphere as a starting structure (left). Within 12 iterations, the averaged density converged to a yeast 80S ribosome (right) that was subsequently used as a purely data-driven de novo template for correlation-based ribosome localization (template matching) in the tomograms. (B) Example cross correlation function (yellow) obtained from template matching against the de novo ribosome structure, superposed with the non-cytosolic cellular volume (gray) excluded from the analysis. Peaks in the cross-correlation function (yellow spots) indicate putative ribosome positions. (C) Distribution of cross-correlation coefficients for the 5000 highest-scoring peaks, which were extracted from the crosscorrelation volume depicted in B while imposing a minimal Euclidean distance of 18.9 nm (9 voxels) between peaks. A Gaussian function (red) was fit to the distribution of coefficients corresponding to true positives. The integral of the Gaussian function corresponds to the number of ribosomes included in the cytosolic volume. (D) Ribosome subtomogram averages obtained for DMSO-treated control (left) and rapamycin-treated (right) cells filtered to 11.5 Å resolution. (E) FSC between subtomogram averages derived from two independent halves of the data (gold standard) for control (blue) and rapamycin- treated (orange) cells. Resolution was determined to 11.5 Å in both cases using the FSC=0.143 resolution criterion. (F) Enlarged view of the region indicated with a box in (D), comparing the ribosome structures from rapamycin-treated (upper panel) and control (lower panel) cells. The most significant density difference (red mesh, threshold level of 6 sigma) between both ribosome structures co-localizes with the Psite tRNA, which is resolved in the control but not the rapamycin-treated.
Related to figure 5. Detected ribosomes are depicted in blue, GEMs in orange and the non-cytoplasmic volume that was excluded from the analysis in gray.
Related to figure 5. Detected ribosomes are depicted in blue, GEMs in orange and the non-cytoplasmic volume that was excluded from the analysis in gray.
(A) After performing hyper- and hypo-osmotic shocks to perturb yeast cell volume and then immediately assessing the diffusion coefficient for 40nm-GEMs, we fit the model (equation 10) for S. cerevisiae and found that it is in very good agreement with our data, suggesting that the Doolittle equation reasonably describes the dependence of diffusion coefficient on volume fraction of crowding agent (), enabling the determination of parameters. (B) We performed the same osmotic stress experiment on mammalian cells and initially measured different parameters. Osmotic stress is known to strongly affect the actin cytoskeleton in mammalian cells, which was confirmed when we depolymerized actin with Latrunculin A concurrent with the osmotic stress: the interaction parameter of the GEMs with the environment increased. When the actin cytoskeleton was stabilized with the JLY cocktail (Peng et al., 2011), we found that the two parameters of the model were closer to the yeast values:: 0.6 is very similar to yeast, suggesting that the interactions of the GEMs with the microenvironment is the same, while is lower, suggesting that mammalian cells are less crowded. (C) and the parameter for cells containing mRNP (inset) were calibrated in order to predict how this particle’s diffusion coefficient would be affected by a change in ribosome concentration caused by rapamycin treatment. (D) For various chemical and genetic conditions, we extracted total nucleic acid by neutral phenol (see methods) and ran the extract on an agarose gel. The gel separates the DNA band (used as a proxy for the amount of cellular material extracted), mRNA, rRNA and tRNA. To assess the relative amount of rRNA, used as a proxy for ribosome abundance, we normalized the band of rRNA to mRNA and subsequently to DNA to get the quantity per cell. This value was determined for each condition and normalized to the control: this gives us the relative change in ribosome quantity in HEK293 drug and siRNA treatments (E) and yeast mutants (F). (G) SUMO10-SIM6-mCherry concentration (measured by flow cytometry) as a function of ribosome concentration (measured by DNA gel) (r2=0.63). (H) SUMO10-SIM6-mCherry concentration (measured by flow cytometry) versus the probability of observing phase separation in the crowding mutants (r2=0.41).
Fluorescent images (top panels) and fluorescent images with single particle trajectories superimposed (bottom panels), for DMSO (vehicle control, left) and rapamycin treated (right) HEK293 cells. Related to figure 2E. Scale bars are 4μm. The movie playback speed is set to 100 frames per second (roughly real time), and the average time between frames is 8 ms. The time stamp shows seconds.
Bright field images (top panels), fluorescent images (middle panels) and fluorescent images with single particle trajectories superimposed (bottom panels), for DMSO (vehicle control, left) and rapamycin treated (right) S. cerevisiae. Related to figure 2D. Scale bars are 5μm. The movie playback speed is set to 100 frames per second (roughly real time), and the average time between frames is 8 ms. The time stamp shows seconds.
In situ cryo-ET of rapamycin-treated yeast cells. Related to figure 5B. The movie slices back and forth in Z through the tomographic volume, then reveals the 3D segmentation of the non-cytosolic volume (grey; aggregates in dark grey) and structures of the 40nm-GEMs (orange), and then reveals the structures of the ribosomes (cyan).
In situ cryo-ET of DMSO-treated control yeast cells. Related to figure 5A. The movie slices back and forth in Z through the tomographic volume, then reveals the 3D segmentation of the non-cytosolic volume (grey) and structures of the 40nm-GEMs (orange), and then reveals the structures of the ribosomes (cyan).
Acknowledgements:
We thank Christophe Renou for initial contributions to this project and Monatrice Lam for additional help with FCS measurements. We thank David Savage for initial suggestions about how to build GEMs. We thank David Morgan, David Drubin, Karsten Weis, Jeremy Thorner, Mike Rosen, Amy Gladfelter, Jef Boeke and Douglas Koshland for advice, strains, plasmids and reagents; William Ludington, Jasna Brujic, Mike Rosen, Jitu Mayor, Ron Vale, Jim Wilhelm, Marcus Taylor, Jan von Skotheim, Roberto Zoncu, Josh Zimmerberg for discussions; and Emily Adney, David Truong, Jef Boeke, John Gerhart, Fred Wilt, Ryan Joyner, Carlos Pantoja, Tim Lionnett, Jon Ditlev, Matthew Maurano, Gabrielle Riekhoff, for help with the manuscript. We acknowledge the help and support of the Janelia Advanced Imaging Center, a facility jointly supported by the Gordon and Betty Moore Foundation and HHMI at HHMI’s Janelia Research Campus in collecting 3D data using the aberration corrected multi-focal microscope – data necessary to validate our 2D simplifications. We thank NYULMC DART Microscopy Laboratory for the consultation and assistance with TEM work. We thank the Alison Killilea and the Cell Culture Core at UC Berkeley for generation and verification of HEK293 cell lines. We gratefully acknowledge funding from the William Bowes Fellows program, the Vilcek Foundation, and the HHMI HCIA summer institute (LJH); the National Science Foundation Graduate Research Fellows Program (GPB). Christine Jacobs-Wagner is an Investigator of the Howard Hughes Medical Institute.
Footnotes
Declaration of interests:
The authors declare no competing interests.
Data Availability:
All subtomogram averages presented in this study have been deposited in the Electron Microscopy Data Bank (EMD-4372, EMD-4373, EMD-4374, EMD-4375), along with the tomograms from figure 5 (EMD-4376, EMD-4377).
References and Notes:
- Akita F, Chong KT, Tanaka H, Yamashita E, Miyazaki N, Nakaishi Y, Suzuki M, Namba K, Ono Y, Tsukihara T, et al. (2007). The crystal structure of a virus-like particle from the hyperthermophilic archaeon Pyrococcus furiosus provides insight into the evolution of viruses. J Mol Biol 368, 1469–1483. [DOI] [PubMed] [Google Scholar]
- Albert S, Schaffer M, Beck F, Mosalaganti S, Asano S, Thomas HF, Plitzko JM, Beck M, Baumeister W, and Engel BD (2017). Proteasomes tether to two distinct sites at the nuclear pore complex. Proceedings of the National Academy of Sciences 114, 13726–13731. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alberti S, and Hyman AA (2016). Are aberrant phase transitions a driver of cellular aging? Bioessays 38, 959–968. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Asano S, Engel BD, and Baumeister W. (2016). In Situ Cryo-Electron Tomography: A Post-Reductionist Approach to Structural Biology (Academic Press; ). [DOI] [PubMed] [Google Scholar]
- Banani SF, Rice AM, Peeples WB, Lin Y, Jain S, Parker R, and Rosen MK (2016). Compositional Control of Phase-Separated Cellular Bodies. Cell 166, 651–663. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Belle A, Tanay A, Bitincka L, Shamir R, and O’Shea EK (2006). Quantification of protein half-lives in the budding yeast proteome. Proc Natl Acad Sci USA 103, 13004–13009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bharat TAM, Russo CJ, Löwe J, Passmore LA, and Scheres SHW (2015). Advances in Single-Particle Electron Cryomicroscopy Structure Determination applied to Sub-tomogram Averaging. Structure 23, 1743–1753. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bishop AC, Ubersax JA, Petsch DT, Matheos DP, Gray NS, Blethrow J, Shimizu E, Tsien JZ, Schultz PG, Rose MD, et al. (2000). A chemical switch for inhibitor-sensitive alleles of any protein kinase. Nature 407, 395–401. [DOI] [PubMed] [Google Scholar]
- Brangwynne CP, Eckmann CR, Courson DS, Rybarska A, Hoege C, Gharakhani J, Jülicher F, and Hyman AA (2009). Germline P granules are liquid droplets that localize by controlled dissolution/condensation. 324, 1729–1732. [DOI] [PubMed] [Google Scholar]
- Brazda P, Szekeres T, Bravics B, Tóth K, Vámosi G, and Nagy L. (2011). Live-cell fluorescence correlation spectroscopy dissects the role of coregulator exchange and chromatin binding in retinoic acid receptor mobility. J Cell Sci 124, 3631–3642. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Broering TJ, Arnold MM, Miller CL, Hurt JA, Joyce PL, and Nibert ML (2005). Carboxyl-proximal regions of reovirus nonstructural protein muNS necessary and sufficient for forming factory-like inclusions. J Virol 79, 6194–6206. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bykov YS, Schaffer M, Dodonova SO, Albert S, Plitzko JM, Baumeister W, Engel BD, and Briggs JA (2017). The structure of the COPI coat determined within the cell. Elife 6, 6916. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cai L-H, Panyukov S, and Rubinstein M. (2011). Mobility of Nonsticky Nanoparticles in Polymer Liquids. Macromolecules 44, 7853–7863. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cai X, Chen J, Xu H, Liu S, Jiang Q-X, Halfmann R, and Chen ZJ (2014). Prion-like polymerization underlies signal transduction in antiviral immune defense and inflammasome activation. Cell 156, 1207–1222. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen Y, Pfeffer S, Hrabe T, Schuller JM, and Förster F. (2013). Fast and accurate reference-free alignment of subtomograms. Journal of Structural Biology 182, 235–245. [DOI] [PubMed] [Google Scholar]
- Cohen MH, and Turnbull D. (1959). Molecular transport in liquids and glasses. The Journal of Chemical Physics 31, 1164–1169. [Google Scholar]
- Daniels BR, Masi BC, and Wirtz D. (2006). Probing single-cell micromechanics in vivo: the microrheology of C. elegans developing embryos. Biophys J 90, 4712–4719. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Di Como CJ, and Arndt KT (1996). Nutrients, via the Tor proteins, stimulate the association of Tap42 with type 2A phosphatases. Genes Dev 10, 1904–1916. [DOI] [PubMed] [Google Scholar]
- Doolittle AK (1952). Studies in Newtonian flow. III. The dependence of the viscosity of liquids on molecular weight and free space (in homologous series). Journal of Applied Physics 23, 236–239. [Google Scholar]
- Duncan R, and Hershey JW (1983). Identification and quantitation of levels of protein synthesis initiation factors in crude HeLa cell lysates by two-dimensional polyacrylamide gel electrophoresis. J Biol Chem 258, 7228–7235. [PubMed] [Google Scholar]
- Eibauer M, Hoffmann C, Plitzko JM, Baumeister W, Nickell S, and Engelhardt H. (2012). Unraveling the structure of membrane proteins in situ by transfer function corrected cryo-electron tomography. Journal of Structural Biology 180, 488–496. [DOI] [PubMed] [Google Scholar]
- Fingerman I, Nagaraj V, Norris D, and Vershon AK (2003). Sfp1 plays a key role in yeast ribosome biogenesis. Eukaryotic Cell 2, 1061–1068. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Förster F, and Hegerl R. (2007). Structure Determination In Situ by Averaging of Tomograms. Methods Cell Biol 79, 741–767. [DOI] [PubMed] [Google Scholar]
- Frangakis AS, Böhm J, Förster F, Nickell S, Nicastro D, Typke D, Hegerl R, and Baumeister W. (2002). Identification of macromolecular complexes in cryoelectron tomograms of phantom cells. Proc Natl Acad Sci USA 99, 14153–14158. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Freeman Rosenzweig ES, Xu B, Kuhn Cuellar L, Martinez-Sanchez A, Schaffer M, Strauss M, Cartwright HN, Ronceray P, Plitzko JM, Förster F, et al. (2017). The Eukaryotic CO2-Concentrating Organelle Is Liquid-like and Exhibits Dynamic Reorganization. Cell 171, 148–162.e19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goddard TD, Huang CC, and Ferrin TE (2007). Visualizing density maps with UCSF Chimera. Journal of Structural Biology 157, 281–287. [DOI] [PubMed] [Google Scholar]
- Grabocka E, and Bar-Sagi D. (2016). Mutant KRAS Enhances Tumor Cell Fitness by Upregulating Stress Granules. Cell 167, 1803–1813.e1812. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guo Q, Lehmer C, Martinez-Sanchez A, Rudack T, Beck F, Hartmann H, Pérez-Berlanga M, Frottin F, Hipp MS, Hartl FU, et al. (2018). In Situ Structure of Neuronal C9orf72 Poly-GA Aggregates Reveals Proteasome Recruitment. Cell 172, 696–705.e12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hara K, Yonezawa K, Weng QP, Kozlowski MT, Belham C, and Avruch J. (1998). Amino acid sufficiency and mTOR regulate p70 S6 kinase and eIF-4E BP1 through a common effector mechanism. Journal of Biological Chemistry 273, 14484–14494. [DOI] [PubMed] [Google Scholar]
- Harmon TS, Holehouse AS, Rosen MK, and Pappu RV (2017). Intrinsically disordered linkers determine the interplay between phase separation and gelation in multivalent proteins. Elife 6, 5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heitman J, Movva NR, and Hall MN (1991). Targets for cell cycle arrest by the immunosuppressant rapamycin in yeast. 253, 905–909. [DOI] [PubMed] [Google Scholar]
- Hou F, Sun L, Zheng H, Skaug B, Jiang Q-X, and Chen ZJ (2011). MAVS forms functional prion-like aggregates to activate and propagate antiviral innate immune response. Cell 146, 448–461. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hrabe T, Chen Y, Pfeffer S, Kuhn Cuellar L, Mangold A-V, and Förster F. (2012). PyTom: A python-based toolbox for localization of macromolecules in cryo-electron tomograms and subtomogram analysis. Journal of Structural Biology 178, 177–188. [DOI] [PubMed] [Google Scholar]
- Hunter GL, and Weeks ER (2012). The physics of the colloidal glass transition. Rep Prog Phys 75, 066501. [DOI] [PubMed] [Google Scholar]
- Jain A, and Vale RD (2017). RNA phase transitions in repeat expansion disorders. Nature 546, 243–247. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Joyner RP, Tang JH, Helenius J, Dultz E, Brune C, Holt LJ, Huet S, Müller DJ, and Weis K. (2016). A glucose-starvation response regulates the diffusion of macromolecules. Elife 5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kaganovich D, Kopito R, and Frydman J. (2008). Misfolded proteins partition between two distinct quality control compartments. Nature 454, 1088–1095. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kwon I, Kato M, Xiang S, Wu L, Theodoropoulos P, Mirzaei H, Han T, Xie S, Corden JL, and McKnight SL (2013). Phosphorylation-Regulated Binding of RNA Polymerase II to Fibrous Polymers of Low-Complexity Domains. Cell 155, 1049–1060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kwon I, Xiang S, Kato M, Wu L, Theodoropoulos P, Wang T, Kim J, Yun J, Xie Y, and McKnight SL (2014). Poly-dipeptides encoded by the C9orf72 repeats bind nucleoli, impede RNA biogenesis, and kill cells. 345, 1139–1145. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lohka MJ, and Maller JL (1985). Induction of nuclear envelope breakdown, chromosome condensation, and spindle formation in cell-free extracts. J Cell Biol 101, 518–523. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luby-Phelps K, Taylor DL, and Lanni F. (1986). Probing the structure of cytoplasm. Journal of Cell Biology 102, 2015–2022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mastronarde DN (2005). Automated electron microscope tomography using robust prediction of specimen movements. Journal of Structural Biology 152, 36–51. [DOI] [PubMed] [Google Scholar]
- Miermont A, Waharte F, Hu S, McClean MN, Bottani S, Léon S, and Hersen P. (2013). Severe osmotic compression triggers a slowdown of intracellular signaling, which can be explained by molecular crowding. Proceedings of the National Academy of Sciences 110, 5725–5730. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mourão MA, Hakim JB, and Schnell S. (2014). Connecting the dots: the effects of macromolecular crowding on cell physiology. Biophys J 107, 2761–2766. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Munder MC, Midtvedt D, Franzmann T, Nüske E, Otto O, Herbig M, Ulbricht E, Müller P, Taubenberger A, Maharana S, et al. (2016a). A pH-driven transition of the cytoplasm from a fluid- to a solid-like state promotes entry into dormancy. Elife 5, e09347. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Munder MC, Midtvedt D, Franzmann T, Nüske E, Otto O, Herbig M, Ulbricht E, Müller P, Taubenberger A, Maharana S, et al. (2016b). A pH-driven transition of the cytoplasm from a fluid- to a solid-like state promotes entry into dormancy. Elife 5, e09347. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nickell S, Förster F, Linaroudis A, Net WD, Beck F, Hegerl R, Baumeister W, and Plitzko JM (2005). TOM software toolbox: acquisition and analysis for electron tomography. Journal of Structural Biology 149, 227–234. [DOI] [PubMed] [Google Scholar]
- Parry BR, Surovtsev IV, Cabeen MT, O’Hern CS, Dufresne ER, and Jacobs-Wagner C. (2014). The bacterial cytoplasm has glass-like properties and is fluidized by metabolic activity. Cell 156, 183–194. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peng GE, Wilson SR, and Weiner OD (2011). A pharmacological cocktail for arresting actin dynamics in living cells. Mol Biol Cell 22, 3986–3994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Petrášek Z, and Schwille P. (2008). Precise Measurement of Diffusion Coefficients using Scanning Fluorescence Correlation Spectroscopy. Biophys J 94, 1437–1448. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Potter CJ, Huang H, and Xu T. (2001). Drosophila Tsc1 functions with Tsc2 to antagonize insulin signaling in regulating cell growth, cell proliferation, and organ size. Cell 105, 357–368. [DOI] [PubMed] [Google Scholar]
- Schaffer M, Mahamid J, Engel BD, Laugks T, Baumeister W, and Plitzko JM (2017). Optimized cryo-focused ion beam sample preparation aimed at in situ structural studies of membrane proteins. Journal of Structural Biology 197, 73–82. [DOI] [PubMed] [Google Scholar]
- Shav-Tal Y, Darzacq X, Shenoy SM, Fusco D, Janicki SM, Spector DL, and Singer RH (2004). Dynamics of Single mRNPs in Nuclei of Living Cells. 304, 1797–1800. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Si K, Choi Y-B, White-Grindley E, Majumdar A, and Kandel ER (2010). Aplysia CPEB can form prion-like multimers in sensory neurons that contribute to long-term facilitation. Cell 140, 421–435. [DOI] [PubMed] [Google Scholar]
- Slaughter BD, Schwartz JW, and Li R. (2007). Mapping dynamic protein interactions in MAP kinase signaling using live-cell fluorescence fluctuation spectroscopy and imaging. Proceedings of the National Academy of Sciences 104, 20320–20325. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Su X, Ditlev JA, Hui E, Xing W, Banjade S, Okrut J, King DS, Taunton J, Rosen MK, and Vale RD (2016). Phase separation of signaling molecules promotes T cell receptor signal transduction. Science 352, 595–599. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Trappe V, Prasad V, Cipelletti L, Segre PN, and Weitz DA (2001). Jamming phase diagram for attractive particles. Nature 411, 772–775. [DOI] [PubMed] [Google Scholar]
- Tsukada M, and Ohsumi Y. (1993). Isolation and characterization of autophagy-defective mutants of Saccharomyces cerevisiae. FEBS Lett 333, 169–174. [DOI] [PubMed] [Google Scholar]
- Waliullah TM, Yeasmin AM, Kaneko A, Koike N, Terasawa M, Totsuka T, and Ushimaru T. (2017). Rim15 and Sch9 kinases are involved in induction of autophagic degradation of ribosomes in budding yeast. Biosci Biotechnol Biochem 81, 307–310. [DOI] [PubMed] [Google Scholar]
- Wang B, Kuo J, Bae SC, and Granick S. (2012). When Brownian diffusion is not Gaussian. Nat Mater 11, 481–485. [DOI] [PubMed] [Google Scholar]
- Warner JR (1999). The economics of ribosome biosynthesis in yeast. Trends Biochem Sci 24, 437–440. [DOI] [PubMed] [Google Scholar]
- Wirtz D. (2009). Particle-tracking microrheology of living cells: principles and applications. Annu Rev Biophys 38, 301–326. [DOI] [PubMed] [Google Scholar]
- Woodruff JB, Ferreira Gomes B, Widlund PO, Mahamid J, Honigmann A, and Hyman AA (2017). The Centrosome Is a Selective Condensate that Nucleates Microtubules by Concentrating Tubulin. Cell 169, 1066–1077.e10. [DOI] [PubMed] [Google Scholar]
- Woodruff JB, Wueseke O, Viscardi V, Mahamid J, Ochoa SD, Bunkenborg J, Widlund PO, Pozniakovsky A, Zanin E, Bahmanyar S, et al. (2015). Centrosomes. Regulated assembly of a supramolecular centrosome scaffold in vitro. 348, 808–812. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zapata-Hommer O, and Griesbeck O. (2003). Efficiently folding and circularly permuted variants of the Sapphire mutant of GFP. BMC Biotechnology 3, 5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang X, Meining W, Fischer M, Bacher A, and Ladenstein R. (2001). X-ray structure analysis and crystallographic refinement of lumazine synthase from the hyperthermophile Aquifex aeolicus at 1.6 A resolution: determinants of thermostability revealed from structural comparisons. J Mol Biol 306, 1099–1114. [DOI] [PubMed] [Google Scholar]
- Zheng SQ, Palovcak E, Armache J-P, Verba KA, Cheng Y, and Agard DA (2017). MotionCor2: anisotropic correction of beam-induced motion for improved cryoelectron microscopy. Nat Meth 14, 331–332. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou H-X, Rivas G, and Minton AP (2008). Macromolecular crowding and confinement: biochemical, biophysical, and potential physiological consequences. Annu Rev Biophys 37, 375–397. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zoncu R, Efeyan A, and Sabatini DM (2011). mTOR: from growth signal integration to cancer, diabetes and ageing. Nat. Rev. Mol. Cell Biol. 12, 21–35. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Results of fitting the blinking anomalous diffusion model to FCS data.
Mutants in the yeast BY4741 background expressing pLH0497. Basal change in diffusion coefficient, and change in the magnitude of the rapamycin effect were measured. Genes deletions that result in a change in basal or greater than 0.5 are highlighted in orange.
The two parameters presented are the change in basal gene diffusion, measured as the ratio of 40nm-GEM diffusion in the mutant as compared to the wild type:
and the magnitude of the rapamycin effect (ε ), measured as the ratio of change in after rapamycin treatment for the mutant vs the wild type change (equation formulated such that ε = 0 indicates no change and ε = 1 indicates that the rapamycin effect is completely lost):
(A) 20nm-GEMs are observed to be 15.39 +/− 0.84 nm by negative stain EM. (B) 40nm-GEMs, which are seen to be 41 nm in high-accuracy in situ cryo-ET, appear to be 37.23 +/− 3.69nm by negative stain EM. (C) The median track length for 40nm-GEMs in DMSO and rapamycin treatment is similar at 35.2 +/− 2.1 and 34.8 +/− 2.2 frames, respectively. Track lengths < 10 displacements were excluded from all analyses (grey shaded area).
(A) The anomalous exponent, a measure of subdiffusive motion, is similar for rapamycin and DMSO treatment in both yeast and HEK293 cells (according a Student’s T-test) but is higher in HEK293 compared to yeast, indicating that mammalian cells are less subdiffusive (p=0.03). (B-I) Cell volume increase, translation, and cytoskeletal perturbations do not explain rapamycin-dependent effects on GEM behavior. (B) Effect of culture saturation on the diffusion coefficent of 40nm-GEMs in BY4741 yeast cells (Normalized Units (N.U.)) (C) Effects of 2 hours of amino acid depletion, 30 minutes of carbon starvation and 30 minutes of nitrogen starvation on the diffusion coefficeint of 40nm-GEMs in BY4741 cells. (D) Effect of rapamycin treatment on the diffusion coefficent of 40nm-GEMs in BY4741 cells over 4 hours. (E) Combined effects of starvation and rapamcyin treatment on the diffusion coefficient of the MS2-tagged GFA1 mRNA. (F and G) Change in coefficient of diffusion (F) and normalized volume (G) over time for rapamycin treatment (orange), cyclohexamide treatment (green), and cell cycle inhibition of the conditional mutant cdc28-as with NMPP1 (blue). (H and I) Actin and microtubule perturbations alter the diffusion of 40nm-GEMs in yeast and mammalian cells but do not abolish the effect of rapamycin. (J) TSC1 was targeted using Silencer Select siRNA (Thermo Fisher). Knockdown was validated by Western blot for Hamartin/TSC1 with a tubulin control using standard techniques (see methods).”
(A) GEM subtomogram averages obtained for DMSO-treated control (left panels) and rapamycin treated (right panels) cells filtered to 26.3 Å resolution. In the central two panels, averages have been sliced open to show the interiors. (B) Fourier shell correlation (FSC) between subtomogram averages derived from two independent halves of the data (gold standard) for control (blue) and rapamycin-treated (orange) cells. Resolution was determined to 26.3 Å in both cases using the FSC = 0.143 resolution criterion. (C) FSC between the two resolution-limited subtomogram averages obtained for control and rapamycin-treated cells. High correlation (FSC > 0.5) within the trustworthy resolution range suggests that GEM structures under both conditions are identical. (D) Gallery of individual GEM particles from control (lower row) and rapamycin-treated (upper row) cells. Each image corresponds to a central tomogram slice through the GEM particle. The amount of cargo within the GEM lumen varies.
(A) 500 manually selected ribosome-containing subtomograms were iteratively aligned with a sphere as a starting structure (left). Within 12 iterations, the averaged density converged to a yeast 80S ribosome (right) that was subsequently used as a purely data-driven de novo template for correlation-based ribosome localization (template matching) in the tomograms. (B) Example cross correlation function (yellow) obtained from template matching against the de novo ribosome structure, superposed with the non-cytosolic cellular volume (gray) excluded from the analysis. Peaks in the cross-correlation function (yellow spots) indicate putative ribosome positions. (C) Distribution of cross-correlation coefficients for the 5000 highest-scoring peaks, which were extracted from the crosscorrelation volume depicted in B while imposing a minimal Euclidean distance of 18.9 nm (9 voxels) between peaks. A Gaussian function (red) was fit to the distribution of coefficients corresponding to true positives. The integral of the Gaussian function corresponds to the number of ribosomes included in the cytosolic volume. (D) Ribosome subtomogram averages obtained for DMSO-treated control (left) and rapamycin-treated (right) cells filtered to 11.5 Å resolution. (E) FSC between subtomogram averages derived from two independent halves of the data (gold standard) for control (blue) and rapamycin- treated (orange) cells. Resolution was determined to 11.5 Å in both cases using the FSC=0.143 resolution criterion. (F) Enlarged view of the region indicated with a box in (D), comparing the ribosome structures from rapamycin-treated (upper panel) and control (lower panel) cells. The most significant density difference (red mesh, threshold level of 6 sigma) between both ribosome structures co-localizes with the Psite tRNA, which is resolved in the control but not the rapamycin-treated.
Related to figure 5. Detected ribosomes are depicted in blue, GEMs in orange and the non-cytoplasmic volume that was excluded from the analysis in gray.
Related to figure 5. Detected ribosomes are depicted in blue, GEMs in orange and the non-cytoplasmic volume that was excluded from the analysis in gray.
(A) After performing hyper- and hypo-osmotic shocks to perturb yeast cell volume and then immediately assessing the diffusion coefficient for 40nm-GEMs, we fit the model (equation 10) for S. cerevisiae and found that it is in very good agreement with our data, suggesting that the Doolittle equation reasonably describes the dependence of diffusion coefficient on volume fraction of crowding agent (), enabling the determination of parameters. (B) We performed the same osmotic stress experiment on mammalian cells and initially measured different parameters. Osmotic stress is known to strongly affect the actin cytoskeleton in mammalian cells, which was confirmed when we depolymerized actin with Latrunculin A concurrent with the osmotic stress: the interaction parameter of the GEMs with the environment increased. When the actin cytoskeleton was stabilized with the JLY cocktail (Peng et al., 2011), we found that the two parameters of the model were closer to the yeast values:: 0.6 is very similar to yeast, suggesting that the interactions of the GEMs with the microenvironment is the same, while is lower, suggesting that mammalian cells are less crowded. (C) and the parameter for cells containing mRNP (inset) were calibrated in order to predict how this particle’s diffusion coefficient would be affected by a change in ribosome concentration caused by rapamycin treatment. (D) For various chemical and genetic conditions, we extracted total nucleic acid by neutral phenol (see methods) and ran the extract on an agarose gel. The gel separates the DNA band (used as a proxy for the amount of cellular material extracted), mRNA, rRNA and tRNA. To assess the relative amount of rRNA, used as a proxy for ribosome abundance, we normalized the band of rRNA to mRNA and subsequently to DNA to get the quantity per cell. This value was determined for each condition and normalized to the control: this gives us the relative change in ribosome quantity in HEK293 drug and siRNA treatments (E) and yeast mutants (F). (G) SUMO10-SIM6-mCherry concentration (measured by flow cytometry) as a function of ribosome concentration (measured by DNA gel) (r2=0.63). (H) SUMO10-SIM6-mCherry concentration (measured by flow cytometry) versus the probability of observing phase separation in the crowding mutants (r2=0.41).
Fluorescent images (top panels) and fluorescent images with single particle trajectories superimposed (bottom panels), for DMSO (vehicle control, left) and rapamycin treated (right) HEK293 cells. Related to figure 2E. Scale bars are 4μm. The movie playback speed is set to 100 frames per second (roughly real time), and the average time between frames is 8 ms. The time stamp shows seconds.
Bright field images (top panels), fluorescent images (middle panels) and fluorescent images with single particle trajectories superimposed (bottom panels), for DMSO (vehicle control, left) and rapamycin treated (right) S. cerevisiae. Related to figure 2D. Scale bars are 5μm. The movie playback speed is set to 100 frames per second (roughly real time), and the average time between frames is 8 ms. The time stamp shows seconds.
In situ cryo-ET of rapamycin-treated yeast cells. Related to figure 5B. The movie slices back and forth in Z through the tomographic volume, then reveals the 3D segmentation of the non-cytosolic volume (grey; aggregates in dark grey) and structures of the 40nm-GEMs (orange), and then reveals the structures of the ribosomes (cyan).
In situ cryo-ET of DMSO-treated control yeast cells. Related to figure 5A. The movie slices back and forth in Z through the tomographic volume, then reveals the 3D segmentation of the non-cytosolic volume (grey) and structures of the 40nm-GEMs (orange), and then reveals the structures of the ribosomes (cyan).
Data Availability Statement
All subtomogram averages presented in this study have been deposited in the Electron Microscopy Data Bank (EMD-4372, EMD-4373, EMD-4374, EMD-4375), along with the tomograms from figure 5 (EMD-4376, EMD-4377).
All subtomogram averages presented in this study have been deposited in the Electron Microscopy Data Bank (EMD-4372, EMD-4373, EMD-4374, EMD-4375), along with the tomograms from figure 5 (EMD-4376, EMD-4377).